POP GOES THE VOLUME
VOLUME OF A CYLINDER, CONE & SHAPE
Investigate volume of a cylinder, cone and sphere by comparing different popcorn containers.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 6 Days
Access each lesson from this unit using the navigation links below
Students will explore the relationship between the area of the base and the height of a cylinder when determining volume. Using this relationship, students will investigate volume in order to determine which figure will hold the most popcorn.
Special thanks goes to Dan Meyer whose Popcorn Picker context inspired the investigation explored during this lesson and the extensions shared throughout the unit.
Intentionality…
In this task, students will explore the relationships between a cylinder, cone and sphere. Using these relationships, students will determine the volume of each figure. This lesson will allow students to develop a deeper understanding of the following big ideas.
- The volume of a 3-dimensional figure can be found by determining the number of cubic units that can be contained within the figure;
- The volume of a prism can be determined by finding the number of cubic units required to cover the base and multiply by the number of layers (i.e.: the height);
- The volume of a pyramid is one-third the volume of a prism with a congruent base and equivalent height. Therefore, the volume of a cone is also one-third the volume of a cylinder with a congruent base and equivalent height;
- Varying the width of the base of a cylinder (i.e.: the diameter) has a greater impact on the volume of a cylinder than varying the height of the cylinder; and,
- The lateral area of two cylinders (i.e.: the surface area of the cylinder excluding the base and top) can be equivalent while producing inequivalent volumes.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the video of a cylinder being made from an 8”x11” piece of paper rolled widthwise and a second cylinder made of the same size paper rolled lengthwise.
Then, ask students:
What do you notice?
What do you wonder?

Give students a reasonable amount of time (eg., 1-2 mins) to do a rapid write, keeping the video paused on the two cylinders side by side
Now invite a whole group conversation centred on student noticings and wonderings. Be sure to record student thinking in a space (eg., whiteboard) visible to all students. This honours the contributions of all students.
Some noticings and wonderings that might emerge are:
- I notice two pieces of paper
- I notice two cylinders
- I notice the cylinders are different sizes
- I notice one cylinder is taller than the other
- I wonder how big the paper is
- I wonder if we’re going to see other shapes
- I wonder if anything is going to happen next
At this point, you can respond to questions that you can cross off the list right away. For example:
- Each piece of paper is the same size
- You could explain who the person is
- You could explain what the person was trying to do
- And so on…
Estimation: Prompt
Now that students have had an opportunity to share their thinking, we can find a landing spot on the first challenge students will focus on:
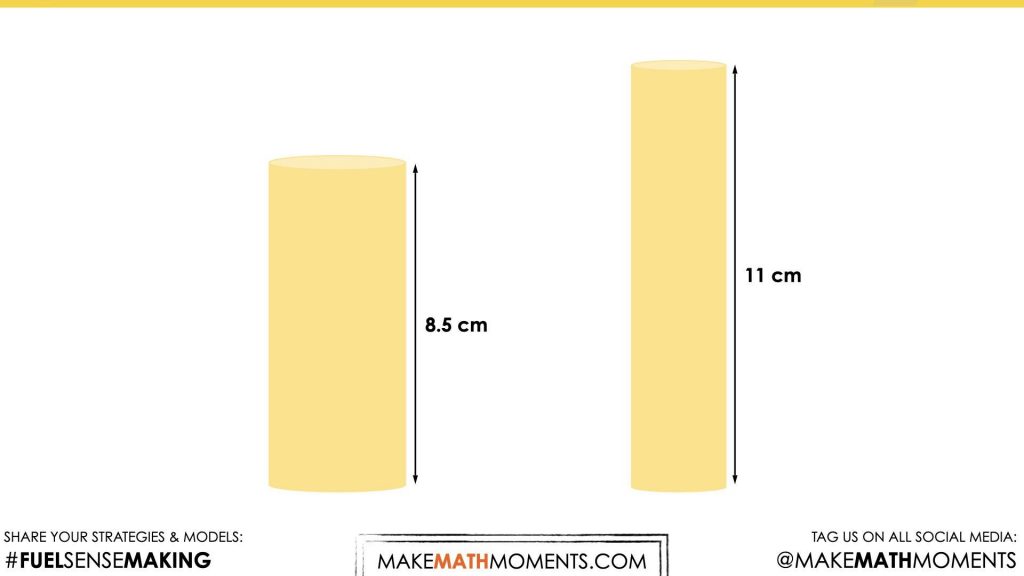
Which cylinder can hold more popcorn?
Make an estimate.
We can now ask students to make an estimate using reasoning and trying to be as strategic as possible. Providing students with an opportunity to make an estimate and try to articulate their thinking with their peers provides a very low floor opportunity for them to not only better understand the context, but to also begin nudging them to think about what will be important to make their estimate more precise as we continue through the lesson.
Ask students to share their estimates, but only their estimates without their thinking or reasoning yet. Invite all estimates into the conversation, and depending on the nature of what is shared and language used, could be an opportunity to discuss concepts, such as understanding quantity relationships and change.
With the image projected, students can be asked what information might be helpful for them to work through the problem. This invites students into the conversation as co-constructors of their own learning. Allow for individual think time, students can then turn and talk to share their thinking in small groups, and finally a whole group discussion. Being strategic in how we respond will help lead students down the curiosity path towards conceptualizing the formula for the volume of a cylinder. By inviting and recording (eg., post-it notes, whiteboard etc,.) all students’ thinking is validated and honoured.
Facilitator Note
Should students need support conceptualizing the formula for area of a circle
be sure to check out Going In Circles! | Exploring Pi: Formula for Circumference of a Circle before working through this unit they, should first check out Going in Circles
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Provide students (or ask students to gather) two 8.5” by 11” pieces of paper for them with the intent of updating their original estimate with a more precise estimate.
Prompt students to:
Use two pieces of 8.5” by 11” paper to create the two cylinders we saw in the video; one created by holding the paper lengthwise and the second by holding the paper widthwise.
Update your estimate.
Consider the following prompts to help guide next moves:
How might you use these cylinders to help you determine which will hold more?
Are there any tools available in the classroom that you might use to help you measure?
Do you have any other tools or strategies you might consider using to help update your estimate to a more precise one?
You might consider having popcorn, unifix cubes, or other non-standard volume units that could be used to help students shift from an estimate to a measured approximation.
Facilitator Notes: Some students may be surprised by the results when building their cylinders from paper, for example, the top and bottom are in the shape of a circle and are the same size. Other students may not notice much of anything, which is an important observation the facilitator can use to help assess how far along the continuum of comparison they might be. Are students struggling to see which two-dimensional shapes are used to compose a cylinder? Are students making a connection to previous learning on creating and using nets to build other three-dimensional figures, such as a triangular-based prism.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse.
Based on what students learned while building their cylinders, they may – or may not – have noticed the relationship between the area of the base and the height. Using student thinking and noticings to drive the conversation, incorporate questions and/or prompts that will centre this learning on this relationship. To support the development of students thinking, consider incorporating questions / prompts that are:
Responsive to Student Thinking, Challenge Student Thinking or Extend Student Thinking.
- Respond to Student Thinking
- Challenge Student Thinking
- Extend Student Thinking
- What information do you have?
- What have you tried so far?
- What do you notice about the faces of a cylinder?
- What information might you need?
- Does this remind you of something?
- Do you see a pattern?
- What do you notice about the information we have about each cylinder?
- What do you notice?
- I wonder if this might work for a different figure or shape that is similar?
- How might you use this information?
Facilitator Note
Consider incorporating a mini-consolidation focusing on the approaches students worked through towards recognizing and understanding what is needed to determine the volume of a cylinder (eg., area of base x height). This will allow for knowledge mobilization so that students can make connections to their own line of thinking and the strategies and/or models shared by classmates.
Throughout the learning to this point, some students may not yet be at a point where they have discovered the relationship between the area of the base and the height.
This is an opportunity to encourage different lines of thinking, which can help students conceptualize the formula for the volume of a cylinder.
Consider prompts such as:
What do you notice about the cylinder with the greater height?
And/or:
What do you notice about the cylinder with the wider base?
Select and Sequence some of the student solution strategies and ask a student from the selected groups to share with the class:
- The most common strategy
- Misconceptions
- Contrasting strategies
- Similar strategies
- Progressive sequence (e.g., a concrete model → symbolic model)
The tools and representations that might surface while students are engaged in the task and are making conjectures with their peers and/or the teacher include:
- Concrete tools (eg., paperclips) to fill each cylinder with
- Generalize to calculate the volume of a cylinder
- Charts and tables; and,
- many others…
Have students share their strategies and reasoning based on what they found from investigating cylinders and determining which one can hold more popcorn Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and level of understanding, rather than ‘fixing’ or ‘funnelling’ student thinking to a strategy and/or a model that does not connect to their strategy and/or approach.
Student Approaches
Student Approach #1: Comparing Cylinders
I found it easy to use the paper to make the cylinders that I wanted. I drew out the lines that I wanted so I could fold the paper, which made my work easier. It was pretty easy to find out which of the two cylinders would hold more popcorn because once they were made I filled each one up with bingo chips and the difference was so large. The cylinder with the wider base held way more bingo chips, and if this is the case, the cylinder with the wider base will hold my popcorn.
Student Approach #2: Building a Model
I found it easy to work through it because my strategy was to use a model and actually try it. The challenging part was actually trying to prove why I could fit more popcorn into the hot dog version of the cylinder. In other words why the volume is bigger when I rolled it that way.
When I rolled the paper like this I wasn’t able to fit as much popcorn as I could fit when I rolled it the other way
When I rolled it like this, the volume was larger. In both cases the area of the base is a circle. In Figure 1, the circle is decided by the width of the rectangular paper. In Figure 2, it is a larger area of the base decided by the length of the rectangle that was rolled and formed the circle at the base. The height of this cylinder is the width of the initial paper.
The area of the circle is a two-dimensional measurement. The height, which is the width of the rectangle I had to roll, is not two-dimensional, but one-dimension and does not make up for the difference between the. In both cases I have to multiply the radius by itself.
The only time when the volume would stay the same is when the initial paper that I had to roll is a square.
Student Approach #3: Understanding π and Applying Volume Formula
Other students who have experience working with Area of a circle and/or volume of a right prism (eg., rectangular-based prism, triangular-based prism) may be able to apply the formula either through reasoning and/or symbolically.
A student who uses reasoning might say:
I knew right away that the height of the cylinder with the wider base had to be 8.5 inches. I saw this in the picture and then tried it out myself and it worked. Since the base of a cylinder is a circle and the circumference of the cylinder with the wider base is 11 inches, I realized that I had to figure out the area of this circle. I know we can use \(πr^2\) to figure this out, but thought we needed some more information in order to solve. I think you noticed that we were stuck because you came over and asked us what we can tell you about different parts of a circle. We started talking and realized that the radius is half the diameter and that π=3.14. So we knew that 3.14 x ?? = 11 and once we figured out what that something (the diameter) is, we could split it in half and that would give us the radius. We thought it would be helpful when we calculate to get rid of the 0.14. Once we did this, we figured the diameter had to be somewhere between 3 and 4 because 3×3=9 and 3×4=12. So we went with 3.5 as the diameter because it’s right in the middle of 3 and 4. and kept π as 3. This got us to 10.5, which is close to 11 and thought that by adding the 0.14 back in we would get even closer to 11. So we kept 3.5 as the diameter and split it in half, which gave us 1.75 as the radius. Now that we had π (or a rounded down version) and the radius, we could get really close to the area of the circle and once we had that, we’d multiply the area of the circle by the height and this would give us the volume. 3×1 gives us 3, but we were having a hard time with the 0.75. We know that 0.75 also means three fourths or 3 one fourths. So if there are 3 one fourths in 1, that means 0.75 x 1 is 0.75. We then took this 0.75 and multiplied it by 3, which got us to 2.25. We then added that to the 3, which gave us 5.25 as the radius and knew we had to double this amount. From here we multiplied 5×5, which we knew was 25. Then we had to figure out what 5 x 0.25 was or what one quarter of 5 is. We know that there are 4 one fourths in 4, and there is 1 one fourth in 1. So we took those 4 one quarters and added them to 1 one quarter, which gave us 5 one quarters or 1.25. We needed another 1.25, which left us with trying to work through 0.25 x 0.25, which was a challenge, so we tried to make things a little easier (and maybe should have done this earlier too). We knew that 0.25 x 1 = 0.25, which means 0.25 x 0.50 must be half of that, or 0.125. So 0.25 x 0.25 must be half of that, or 0.06. We then added 25+1.25+1.25+0.06 = 27.56. We knew we had to triple this because of π, which would get us to 82 or 83. We rounded down to 82 to keep it safe and then knew we had to multiply this by the height of the cylinder. Once we did this, we knew how much popcorn this cylinder could hold.
A student who has experience using the formula symbolically might show:
V = \(πr^2\) x h = (3.14)(5.5 x 5.5) (8.5) = 807.37 Since the diameter is 11, I split that in half to get the radius. I then multiplied the radius by itself, took the product of that to multiply by 3.14 and then multiplied that total to get to the volume, which is 807.37㎤
Next Moves
Consolidation
To prepare for a meaningful consolidation be sure to gather work samples or make note of student ideas to be highlighted. It is worth considering that there are several ways to focus on a meaningful consolidation. But the goal is to highlight student thinking/ideas/approaches that surfaced while working through the task. By engaging with students in a meaningful dialogue that builds on their understanding of the math concepts addressed, students are positioned to make connections to their own learning or strategies used, and those shared by their classmates and peers.
By facilitating a mini-consolidation early on in the task about the relationship between the area of the base and the height of a cylinder, students will have had an opportunity to discuss this exploration.
However, it might be worth revisiting here and having students speak to this relationship and how it supported them working through determining which cylinder would hold more popcorn, or in other words, has the greater volume.
What emerges during the task will inform how student work is sequenced during consolidation.
Consider leveraging the visuals from the consolidation silent solution animation video below to explicitly highlight that the volume of a cylinder can be found in the same manner that we find the volume of any prism; by multiplying the area of the base times the height.
In the video, we begin by showing cylindrical representations of each popcorn container.
We begin with the cylinder with a height of 8.5 cm and use the non-standard unit of popcorn kernels to measure the area of the base.
While the view from the top makes one believe that the popcorn kernels are two-dimensional and therefore a great unit of measure for area, flipping the base to a side-view explicitly highlights that the popcorn kernels are actually better used to represent a 3-dimensional unit of volume. Therefore, the volume of a 1 kernel tall cylinder (in this case, we’re assuming each kernel has an average height of 1 cm) would be 33 popcorn kernels (or cubic popcorn kernels).
We can then scale this up additively by iterating these 1 cm tall cylinders on top until we arrive at 8.5 cm tall, or multiplicatively scale by multiplying the single 1 cm tall cylinder by a factor of 8.5 to get the height and volume of our full cylinder.
We repeat the process for the 2nd cylinder to explicitly highlight that the volume of the cylinder can be found by determining the area of the base (or the volume of the ‘base layer’) and multiplying by the height (or the number of layers).
It is now clear to all students that the shorter, wider cylinder holds the most popcorn.
A prompt you might consider asking includes:
What measurements impact the volume of a cylinder?
Do some measurements have a greater impact on the volume than others?
Two of the big ideas we are hoping to emerge from this lesson include:
- varying the width of the base (diameter) has a greater impact on the volume of a cylinder than varying the height of the cylinder; and,
- the lateral area of two cylinders can be equivalent while producing inequivalent volumes.
Through this activity, we would like students to make the connection that as the diameter of the base varies, the impact is two dimensional (i.e.: of degree 2). This means that as the diameter increases, the “length” and “width” of the cylinder are both increasing. Conversely, varying the height is one dimensional (i.e.: of degree 1) which means that the volume is only growing in one dimension thus growing the volume less dramatically.
Facilitator Note:
It is very important to consider the language used as different strategies, approaches and solutions are discussed. While some of the student samples highlighted may demonstrate different levels of sophistication, all student thinking needs to be respected and honoured, knowing that learning mathematics is developmental and students make sense of the learning based on where they are in their learning journey.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
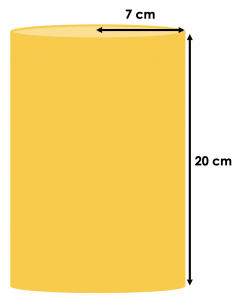
Consolidation Prompt #1:
The radius of a cylindrical container is 7 cm.
The height of the container is 20 cm.
Without the use of a calculator, about how much popcorn can this container hold?
Consolidation Prompt #2:
What might a general rule be for how you could tell whether two different cylinders with the same lateral area (area of the “curved side”) will have the greater volume? Convince your peers.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!