Pop Goes the Volume [Day 5] Volume of three-dimensional figure

POP GOES THE VOLUME [DAY 5]

VOLUME OF A CYLINDER, CONE & SHAPE

Investigate volume of a cylinder, cone and sphere by comparing different popcorn containers.

Learn how to best use our lessons and units of study

Intentionality

Math Talk

Visual Math Talk Prompt #1

Visual Math Talk Prompt #2

Visual Math Talk Prompt #3

Spark Curiosity

Fuel Sensemaking

During Moves

Next Moves

Reflect and Consolidation Prompts

Resources & Downloads

Educator Discussion Area

Teach This Lesson

Facilitate this lesson with students!

PRESENTATION MODE

Intentionality & Unit Overview

Length of Unit: 6 Days

Access each lesson from this unit using the navigation links below

Students will explore the relationship between a cylinder, cone and sphere when calculating volume. Through this investigation, students will have opportunities to begin to conceptualize that the volume of a sphere is \(\frac{2}{3}\) the volume of a cylinder, provided the cylinder’s height is equal to the diameter, or twice the radius of the sphere.

Intentionality…

This task will allow students to develop a deeper understanding of big ideas.

Some of the big ideas that will likely emerge in this task include:

The volume of a 3-dimensional figure can be found by determining the number of cubic units that can be contained within the figure;
The volume of a prism can be determined by finding the number of cubic units required to cover the base and multiply by the number of layers (i.e.: the height);
The volume of a pyramid is one-third the volume of a prism with a congruent base and equivalent height. Therefore, the volume of a cone is also one-third the volume of a cylinder with a congruent base and equivalent height;
The volume of a sphere is double the volume of a cone with an equivalent radius and equivalent height; and,
The volume of a sphere is 2 thirds the volume of a cylinder with an equivalent radius and equivalent height.

Math Talk

The following sequence of problems provides an opportunity for students to conceptualize the ratio relationships between the volume of a cylinder, cone and sphere.

In particular, these visual math talk prompts will highlight that calculating the volume of any cone or sphere begins with finding the volume of a cylinder with the same radius and height.

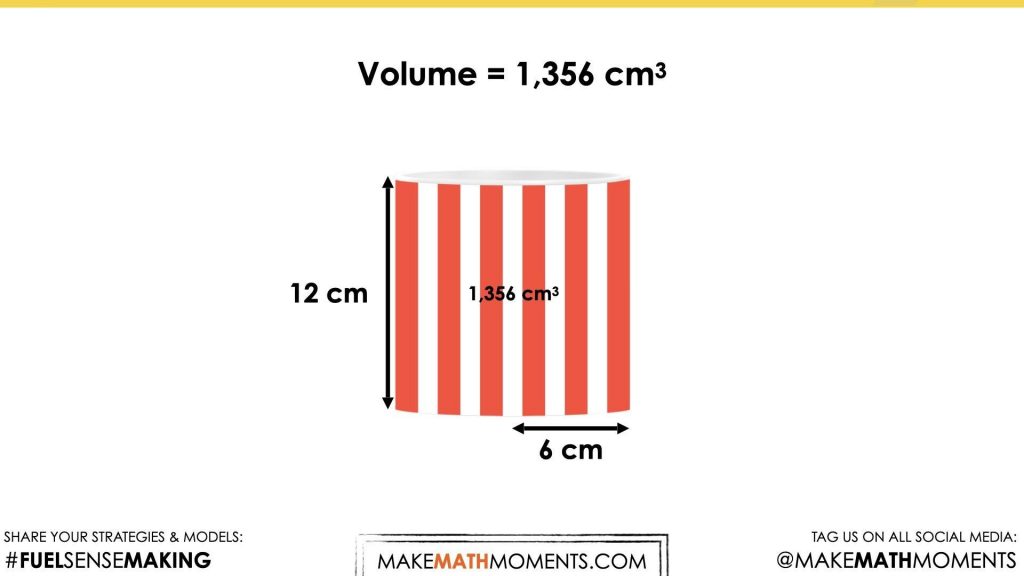
Visual Math Talk Prompt #1

Show students the following visual math talk prompt and be prepared to pause the video where indicated:

Then ask students:

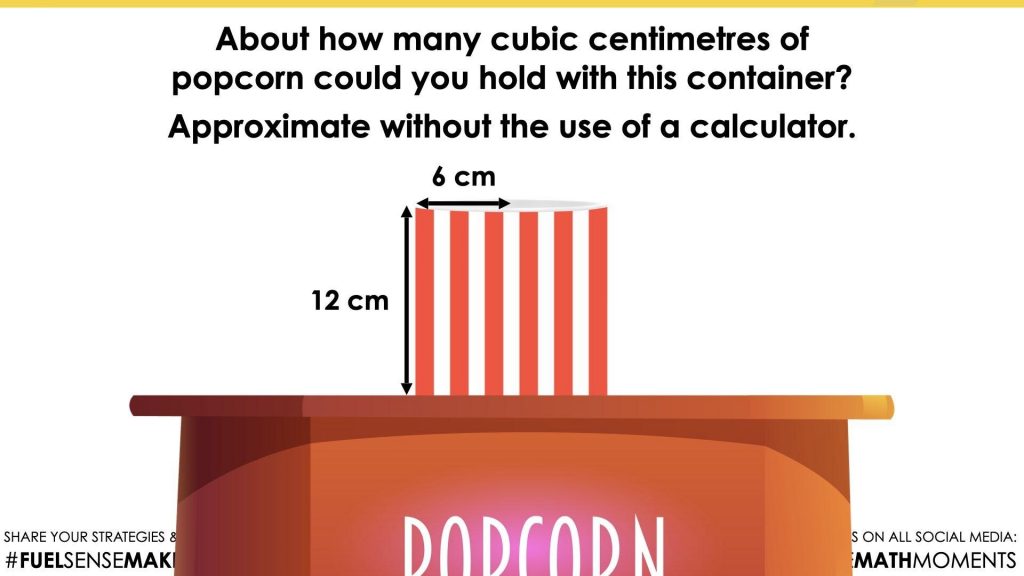
About how many cubic centimetres of popcorn could you hold with this container?
Approximate without the use of a calculator.

With the image projected, give students a reasonable amount of time to reflect on and then work through the question, with strong consideration given to student collaboration as they reason and think their way through to what the volume of this cylinder might be.

After a reasonable amount of time, invite students to share their approximations/calculations.

The goal is to once again get students to think about how they can approximate the area of the base and use this quantity to then scale vertically to reveal a reasonable quantity for the volume.

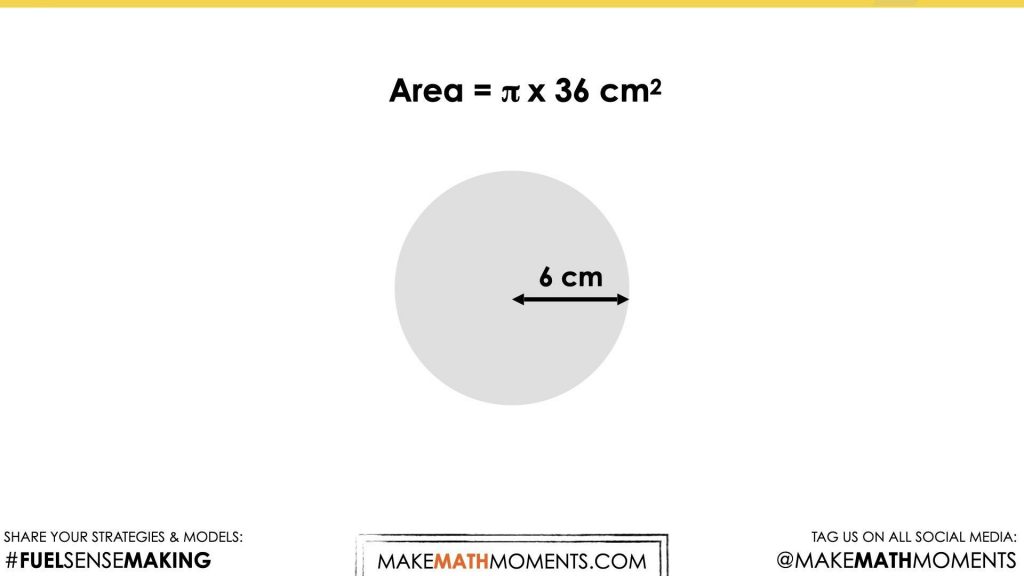
At this point, students may be more inclined to simply use the formula for area of a circle rather than decomposing the circle into a rectangle as we had done earlier in the unit.

Since the radius is 6 cm and 6 cm squared is 36 cm squared, about 3 times this quantity will give an area of about 108 square centimetres. Students using a calculator will likely land somewhere around 113 square centimetres. Be sure to celebrate those who approximated and then adjusted up rather than simply punching into a calculator.

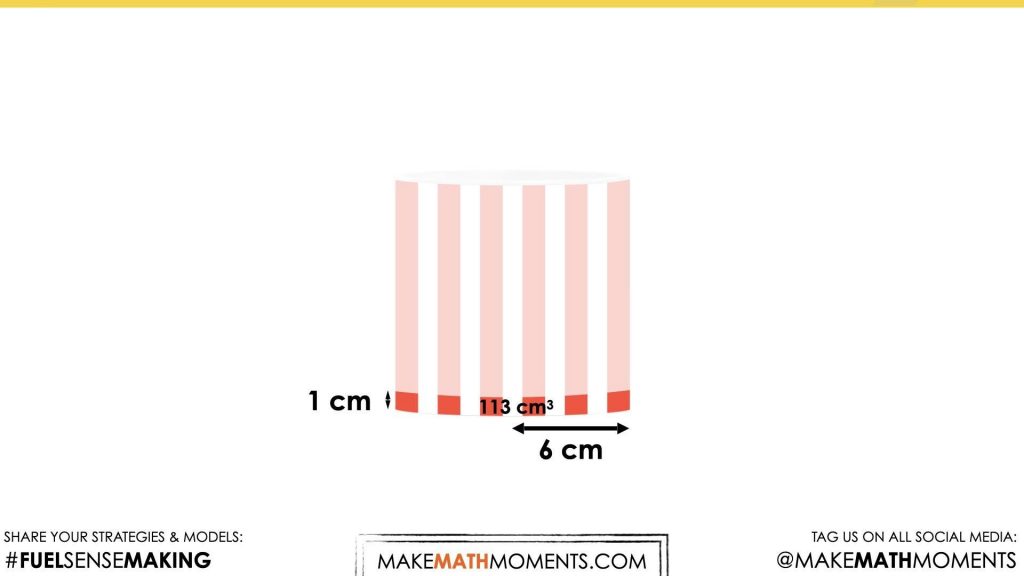
With the area of the base now known, we can conclude that we now have the volume of a 1 cm tall cylinder; approximately 113 cubic centimetres.

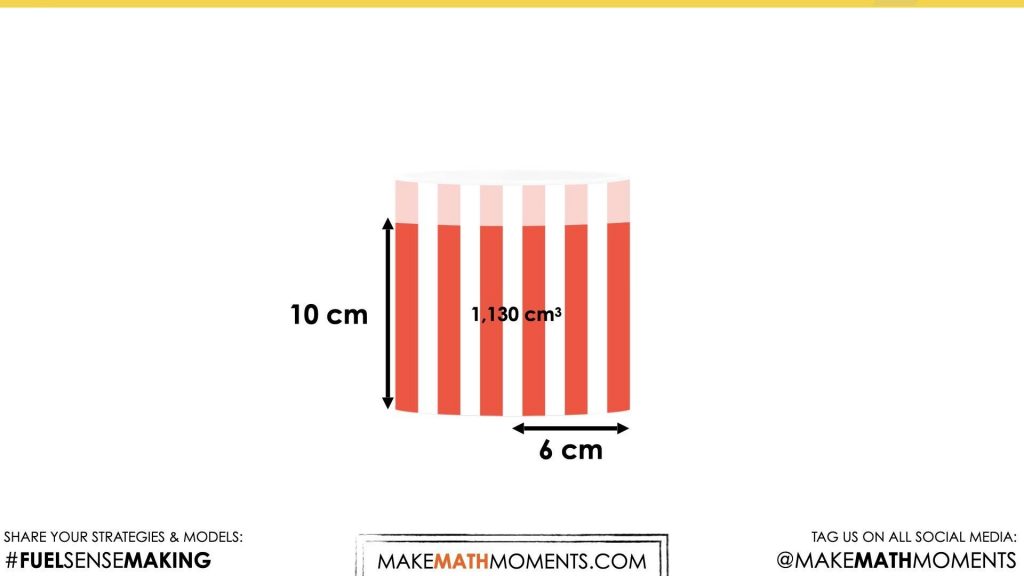
From here, students can scale the height of the cylinder upwards using a partial products approach until reaching the desired height of 12 centimetres.

Students who arrive at a total volume of between 1,290 and 1,380 cubic centimetres are demonstrating a pretty high level of precision without leveraging the use of a calculator.

Be sure to record student thinking in a space (eg., whiteboard) visible to all students. This honours the contributions of all students.

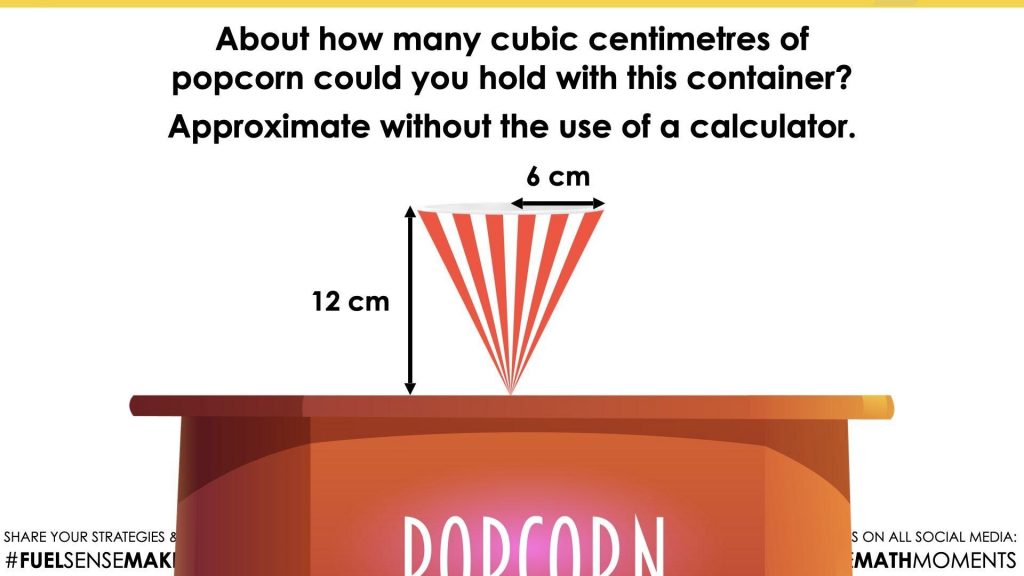
Visual Math Talk Prompt #2

Show students the following visual math talk prompt and be prepared to pause the video where indicated:

Then ask students:

About how many cubic centimetres of popcorn could you hold with this container?
Approximate without the use of a calculator.

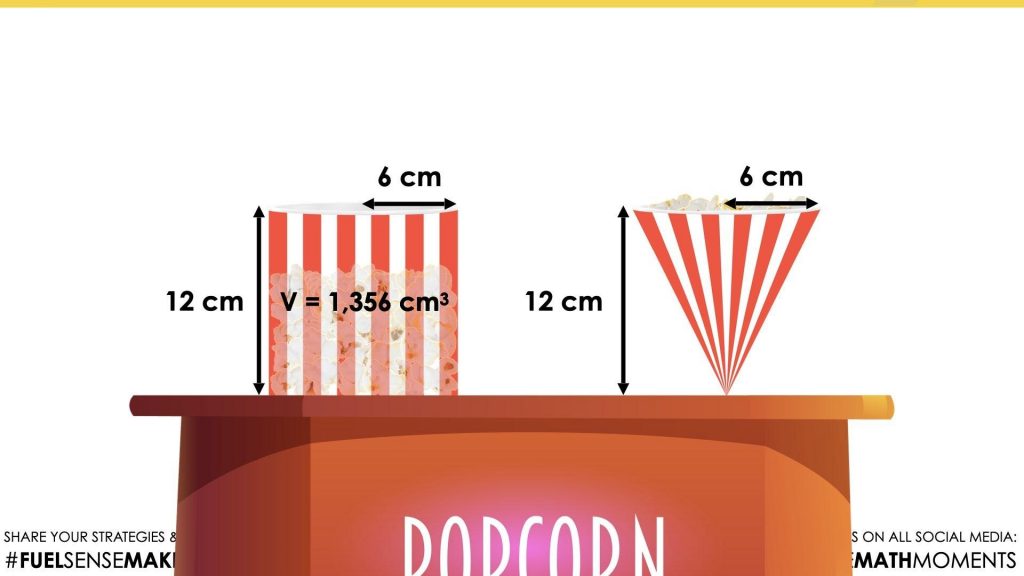
Since this cone has the same height and radius as the cylinder in Visual Math Talk Prompt #1, the intent is to promote students reasoning with the volume relationships that have been uncovered throughout this unit.

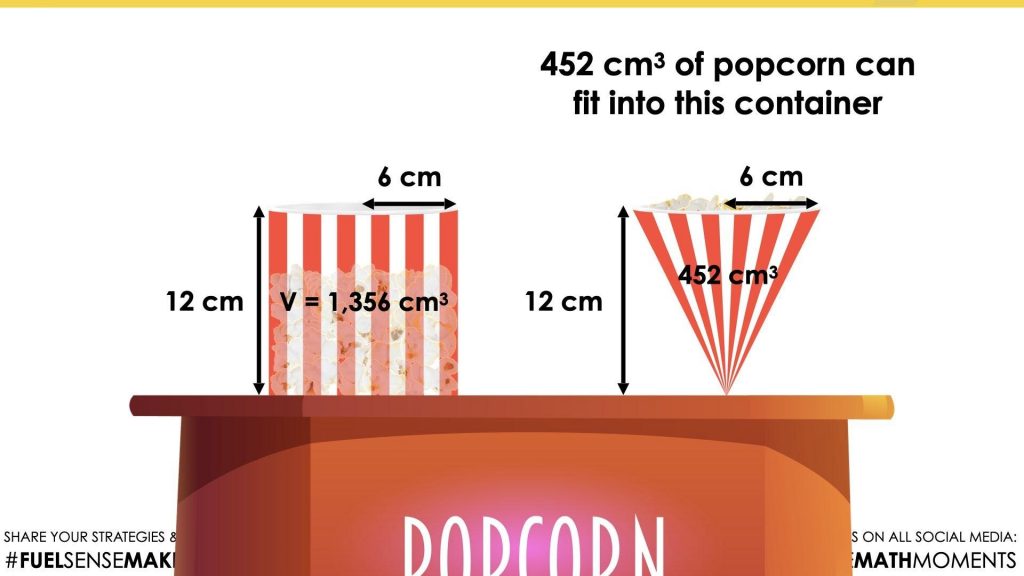
Since we know that the volume of 3 cones is equivalent to the volume of 1 cylinder with the same height and radius, simply taking 1 third of the volume of the cylinder is a highly efficient approach that some students might choose to use.

Since 1 third of 1,350 cubic centimetres is 450 centimetres cubed, an answer within a 50 to 100 cubic centimetre range would be reasonable for those working without a calculator.

Visual Math Talk Prompt #3

Login/Join to access additional Visual Math Talk Prompts as well as the Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

Spark Curiosity

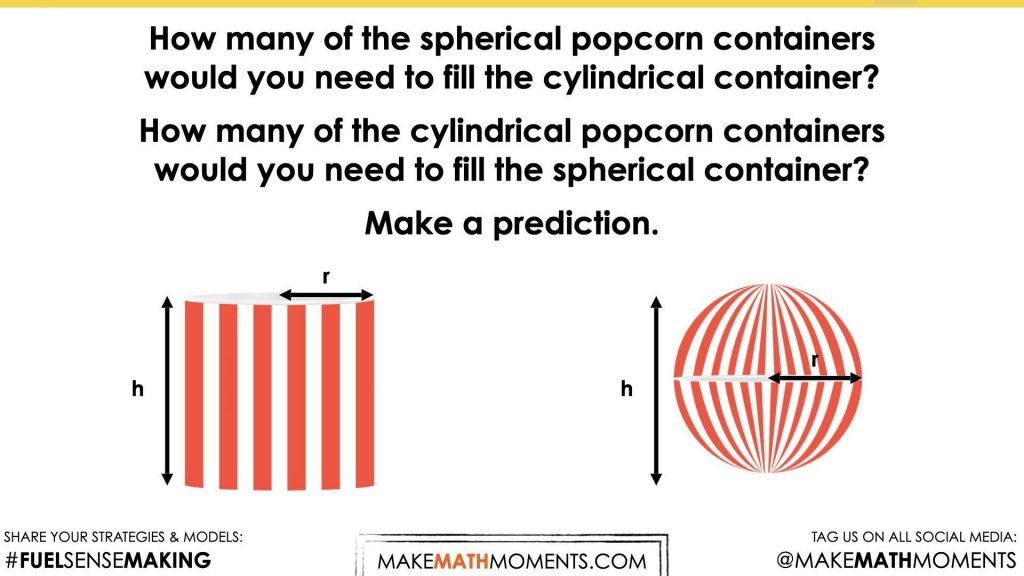
Prediction Prompt

Prompt students with:

How many spherical popcorn containers can you fit in the cylindrical container? Make an estimate.

Give 30-60 seconds for individual think-time before offering students an opportunity to share their thinking with a classmate and then a whole group share.

To support learning during the investigation, students can use manipulatives from an available math kit, such as geometric solids. Alternatively, the visuals provided during the lesson can also be used.