POP GOES THE VOLUME [DAY 3]
VOLUME OF A CYLINDER, CONE & SHAPE
Investigate volume of a cylinder, cone and sphere by comparing different popcorn containers.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 6 Days
Access each lesson from this unit using the navigation links below
Students will explore the relationship between the volume of a cylinder and the volume of a cone. Using this relationship, students will investigate volume in order to determine which container will hold the most popcorn.
Intentionality…
Through this investigation, students compare the volume of a cylindrical popcorn container and a conical popcorn container with the same radius and height to generalize the formula for calculating the volume of a cone as:
Volume of A Cone = Volume of Same Base Cylinder and Height Divided By 3
This lesson will allow students to develop a deeper understanding of big ideas.
Some of the big ideas that will likely emerge in this task include:
- The volume of a 3-dimensional figure can be found by determining the number of cubic units that can be contained within the figure;
- The volume of a prism can be determined by finding the number of cubic units required to cover the base and multiply by the number of layers (i.e.: the height);
- The volume of a pyramid is one-third the volume of a prism with a congruent base and equivalent height. Therefore, the volume of a cone is also one-third the volume of a cylinder with a congruent base and equivalent height;
- Varying the width of the base of a cylinder (i.e.: the diameter) has a greater impact on the volume of a cylinder than varying the height of the cylinder; and,
- The lateral area of two cylinders (i.e.: the surface area of the cylinder excluding the base and top) can be equivalent while producing inequivalent volumes.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following animation of two popcorn containers – a cylinder and cone with the same radius and height – being filled with popcorn until full.
With the image projected, give students 30 seconds to 1 minute of think time to reflect on anything they may have noticed or might be wondering about.
Then students will do a quick turn and talk to share their noticings and wonderings with a classmate.
After a reasonable amount of time, invite students into a whole class discussion to share their thinking.
Continue to honour the contributions of all learners by recording student thinking in a space (eg., whiteboard) visible to all.
Some noticings and wonderings that might emerge are:
- I notice a lot of popcorn.
- I notice two different containers.
- I notice a cylinder and a cone.
- I notice the cone container filled much faster than the cylinder.
- It seems that the cylinder can hold much more popcorn than the cone.
- I wonder how much popcorn there is?
- I wonder how long it would take to make all that popcorn?
- I wonder where the popcorn came from?
- I wonder how much more popcorn you’d get if you bought the cylinder container instead of the cone?
Estimation: Prompt
Now that students have had an opportunity to share their thinking, we can find a landing spot for the problem students will focus on:
How much more popcorn can the cylinder hold than the cone?
Make an estimate.
We can now ask students to make an estimate using reasoning and trying to be as strategic as possible. Providing students with an opportunity to make an estimate and try to articulate their thinking with their peers provides a very low floor opportunity for them to not only better understand the context, but to also begin nudging them to think about what will be important to make their estimate more precise as we continue through the lesson.
Follow up that question with:
How might we convince someone that the quantity you came up with is correct?
Let students loose to make some estimates based on what they saw.
Fuel Sense-making
Investigate
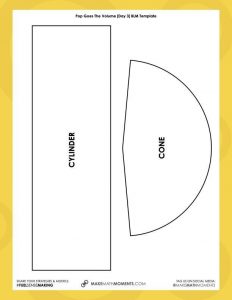
Provide students with fillable 3D geometric solids of a cylinder and a cone with the same radius and height to investigate by filling with water, sand, rice or similar.
Alternatively, consider giving students the net of a cylinder and a cone with the same radius and height to allow them to construct the cylinder and cone out of paper and explore by filling with rice, beads, or similar.
Prompt students to:
Investigate using manipulatives or by constructing using the templates provided.
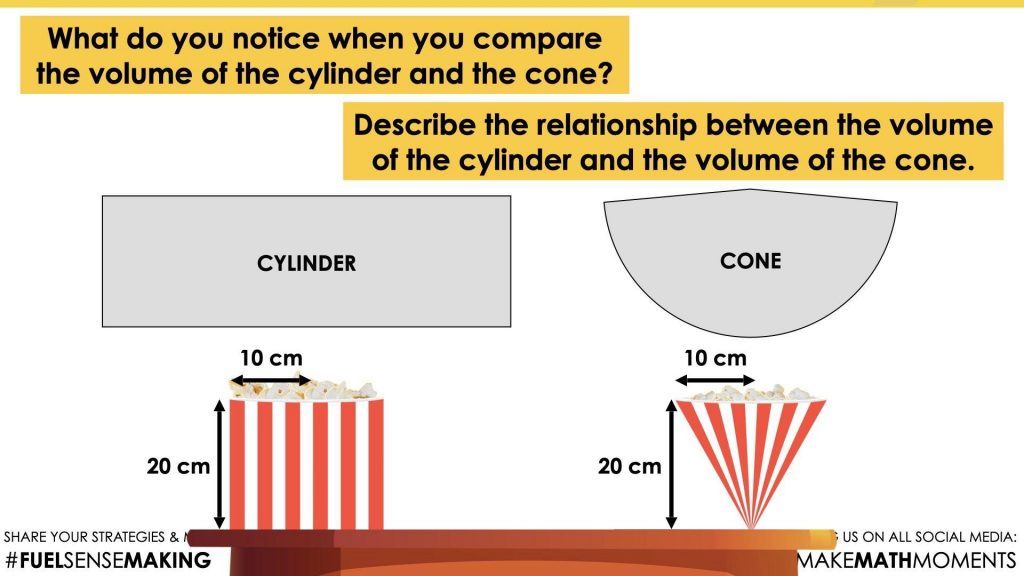
What do you notice when you compare the volume of the cylinder and the cone?
Describe the relationship between the volume of the cylinder and the volume of the cone.
Some students may be surprised by the results when building their three-dimensional figures from paper. For example, some students might be surprised to see the size difference between the two. Other students may not notice much of anything, which is an important observation the facilitator can use to determine purposeful questions to help students take note of the volume the cone is missing in comparison to the cylinder.
Facilitator Note:
Having various manipulatives and/or tools available will support students in building concrete models and simulating what they saw in the video/animation at the beginning of the lesson. Counters or beads can be easily substituted for popcorn.
During Moves
While Students Are Investigating…
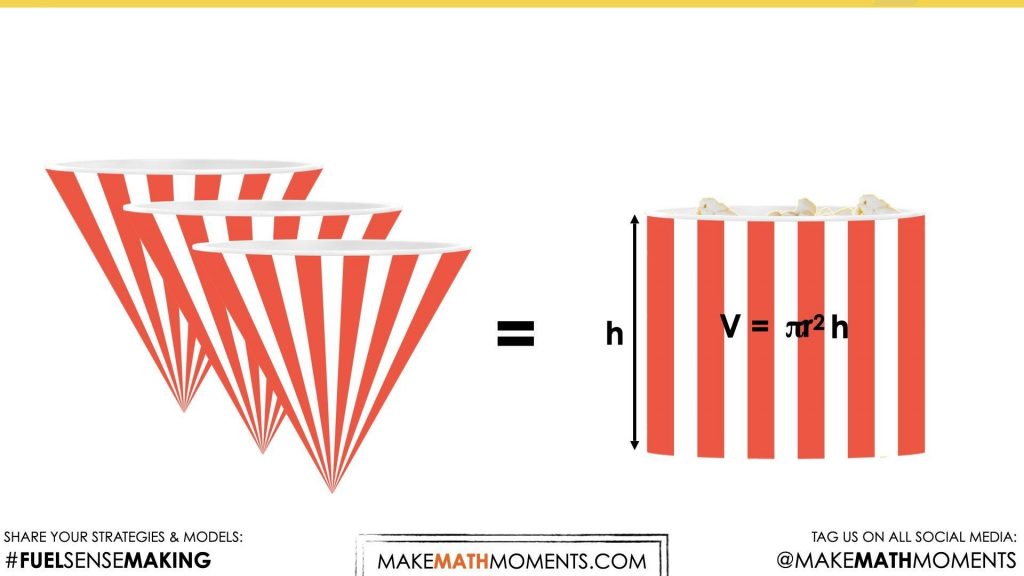
Students will have an opportunity to investigate how many times they’ll need to fill up a cone with popcorn in order to refill the cylinder, leading to the discovery that it takes 3 cones to completely refill the cylinder. This will help students conceptualize that the cone’s volume is \(\frac{1}{3}\) of the cylinder, thus generalizing that the volume of a cone is \(\frac{1}{3}\) the volume of a cylinder. As students are working, you might consider using this opportunity to pose purposeful questions and document student thinking for the purpose of formative assessment.
Pay close attention to the strategies that students are using.
Are students:
- Using Manipulatives and Concrete Tools (eg., unifix cubes, counters)?
- Understanding the relationship and beginning to generalize the formula for volume of a cone?
Student Approaches
Student Approach #1: Spatial Reasoning
I can see that the cylinder from yesterday looks bigger than the cone. So I think at least one cone can fit into the cylinder. I’m also pretty sure we might be able to get a second cone in the cylinder, but we might have to move things around a little bit so both of them can fit. So I think I’d need to play around with the shapes a little more.
Student Approach #2: Proportional Reasoning
By looking at the image, I noticed that the cylinder is at least twice the size of the cone, so I know we can fit at least two cones in the cylinder. But I think there might be some space left over after we’ve fit two cones into the cylinder, I’m just not sure how much. So I think the cylinder is probably 2-3 times bigger than the cone.
Student Approach #3: Physically Filling
Using rice, I filled the cylinder using 3 “scoops” of the cone, so therefore I know that the volume of the cylinder is 3 times as great as the cone. In other words, the volume of the cone is 1 third as great as the cylinder.
Consolidation
The purpose of this lesson is to emerge the volume 3 to 1 ratio relationship between a cone and a cylinder. While it is fantastic for those students who land on this relationship through the investigation, we must ensure that all students walk away with this understanding.
Consider prompts such as:
What do you notice about the volume relationship between the cone and cylinder?
How might you describe the volume relationship?
How might we describe a formula for finding the volume of a cone?
When ready, invite students to share their strategies and reasoning based on what they found from investigating the cylinder, the cone and determining the number of times the cone needs to be filled with popcorn in order to refill the cylinder. Note whether students are using additive thinking (i.e.: the cylinder holds 2 more cones) or multiplicative thinking (i.e.: the cylinder has 3 times the volume of the cone).
Discuss their strategies and elicit student thinking to build off of their current prior knowledge and level of understanding, rather than ‘fixing’ or ‘funnelling’ student thinking to a strategy and/or a model that does not connect to their strategy and/or approach.
This silent solution video can be used to both consolidate and reveal the 3 to 1 ratio relationship that exists between the volume of a cone and volume of a cylinder and can be used to assist in making explicit connections at this point.
In the video, students will see two sets of quantities that are intended to highlight the 3 to 1 ratio relationship between the volume of a cone and volume of a cylinder:
24 seconds to fill the cylinder vs. 8 seconds to fill the cone; and,
60 kernels of popcorn in the cylinder vs. 20 kernels of popcorn in the cone.
At this point, it is worth pausing to ask students to:
Describe how to calculate the volume of any cone.
The goal is to once again highlight that we can take 1 third of the volume of a cylinder since that quantity is equivalent to the volume of a cone with the same radius and height.
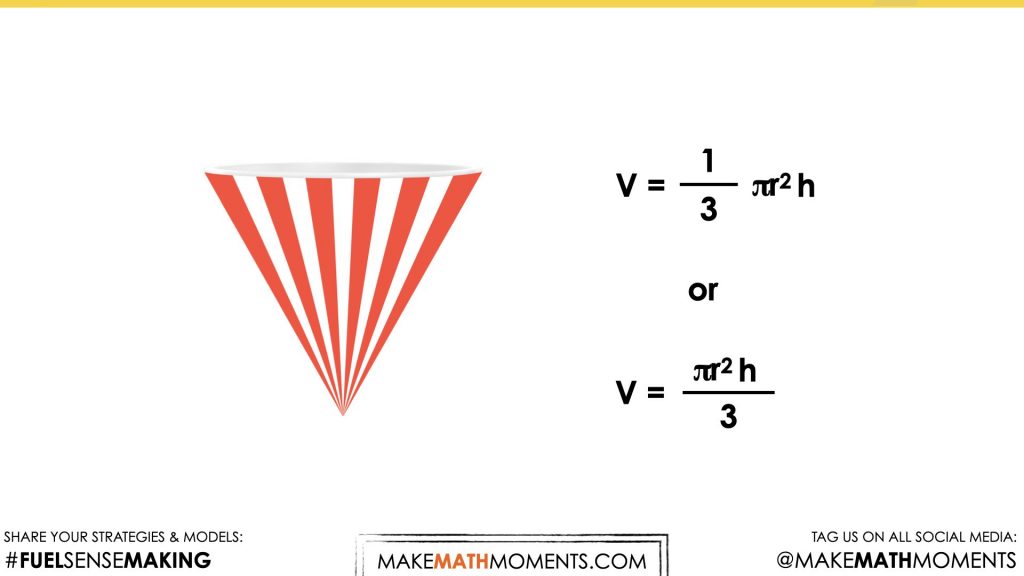
From here, we want to ensure that students can not only describe how to calculate the volume of a cone, but can also represent this formula algebraically as:
V = \(\frac{πr^2h}{3}\)
or
V = \((\frac{1}{3})πr^2h\)
This video and corresponding images will be shared in the Reveal tab in the lesson.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Consolidation Prompt #2:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Consolidation Prompt #3:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
You might choose to simply open the printable PDF handout to display on your display or download and print for students.
Resources & Downloads
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!