POP GOES THE VOLUME [DAY 2]
VOLUME OF A CYLINDER, CONE & SHAPE
Investigate volume of a cylinder, cone and sphere by comparing different popcorn containers.
Intentionality
Math Talk
Visual Math Talk Prompt #1
Visual Math Talk Prompt #2
Visual Math Talk Prompt #3
Visual Math Talk Prompt #4
Spark Curiosity
Fuel Sensemaking
Next Moves
Consolidation
Purposeful Practice
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 6 Days
Access each lesson from this unit using the navigation links below
Students will investigate the relationship between the area of the base and height and the volume of a cylinder
Intentionality…
The purpose of the Day 2 activities is to reinforce the concepts from Day 1. Students will engage in a meaningful problem through a math talk and will have an opportunity to complete independent purposeful practice. The math talk and purposeful practice serve to develop a deeper understanding of the following big ideas:
Some of the big ideas that will likely emerge in this task include:
- The volume of a 3-dimensional figure can be found by determining the number of cubic units that can be contained within the figure;
- The volume of a prism can be determined by finding the number of cubic units required to cover the base and multiply by the number of layers (i.e.: the height);
- The volume of a pyramid is one-third the volume of a prism with a congruent base and equivalent height. Therefore, the volume of a cone is also one-third the volume of a cylinder with a congruent base and equivalent height; and,
- Varying the width of the base of a cylinder (i.e.: the diameter) has a greater impact on the volume of a cylinder than varying the height of the cylinder.
Math Talk
The following sequence of related problems provides an opportunity for students to build on their learning from Day 1 by working through the volume of a cylinder with missing dimensions or limited information. This provides a context for students to investigate different approaches for determining the volume of a cylinder by grounding their thinking in the relationship between the area of the base and the height of a cylinder. In the previous lesson, we explored the context for comparing two cylinders in order to determine which one has the greatest volume. This context was helpful for building conceptual understanding supporting students in their understanding of Pi, π, and generalizing for how to calculate the volume of a cylinder.
Visual Math Talk Prompt #1
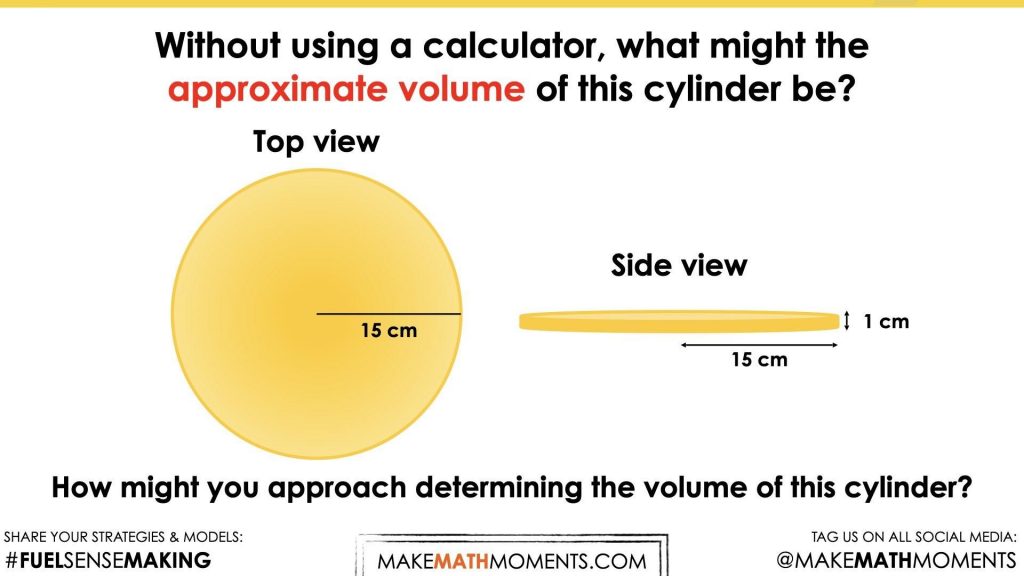
Show students the following animation of a cylinder being ‘constructed’ with a radius of the base of 15 cm and a height of the cylinder of 1 cm:
Then ask students:
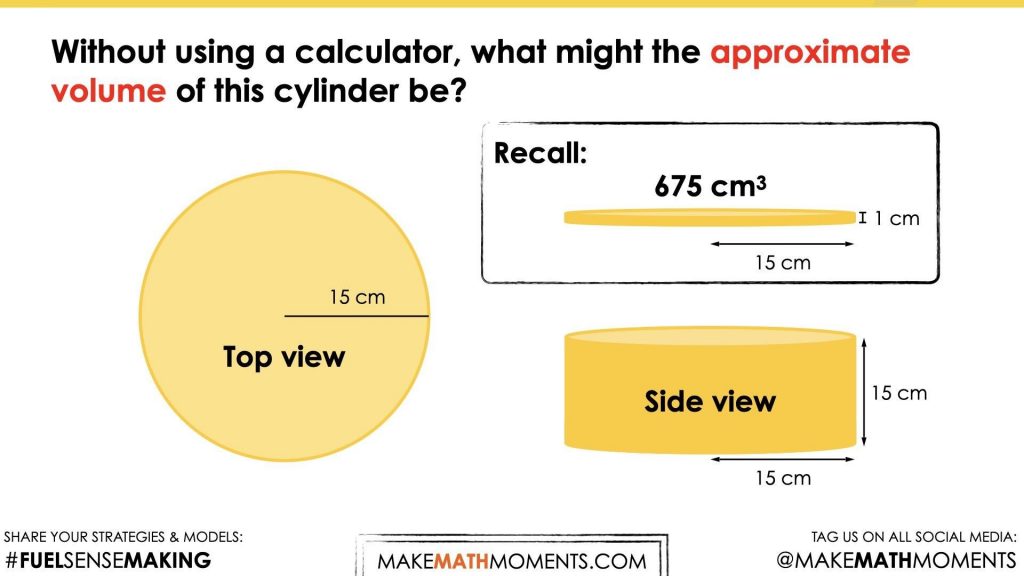
Without using a calculator, what might the approximate volume of this cylinder be?
How might you approach determining the volume of this cylinder?
The purpose here is for students to rely on their understanding of the area of a circle (needed for calculating the area of the base) prior to adding in a height beyond 1 ‘layer’ of cubic centimetres.
With the image projected, give students 30 seconds to 1 minute to reflect on the question. Then students will do a quick turn and talk to share their thinking with a classmate.
After a reasonable amount of time, invite students to share their approximations.
Be sure to record student thinking in a space (eg., whiteboard) visible to all students. This honours the contributions of all students.
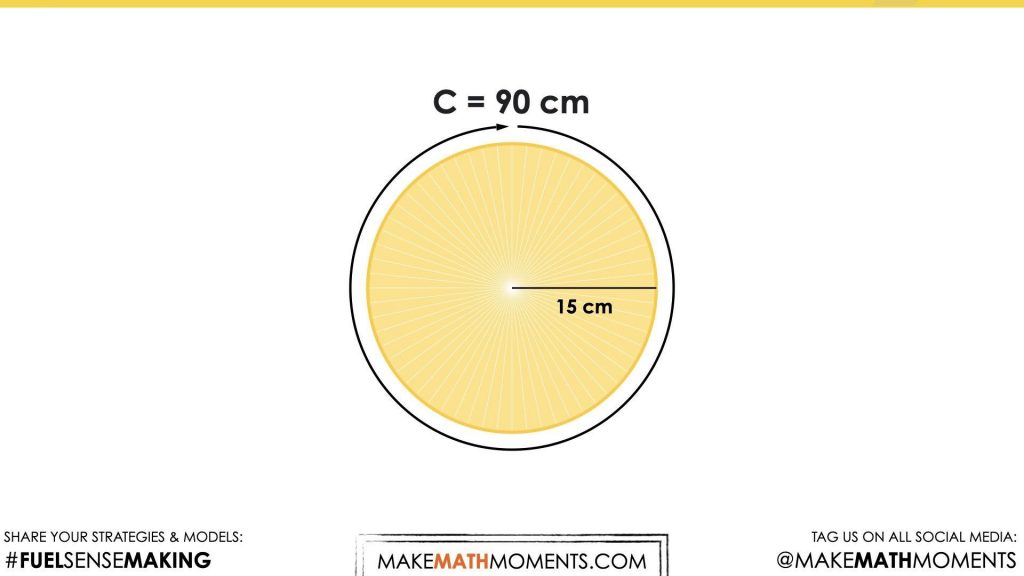
The intention of this math talk is to get students using the relationship of the diameter of a circle to its radius (Pi, π) to determine an approximate circumference. Since the radius is 15 cm, the diameter of the circular base is 30 cm and we can use our understanding that the circumference of a circle is approximately 3 “and a bit” (Pi, π) times as long as the diameter.
A reasonable estimate for the circumference would be between 90 cm and 95 cm.
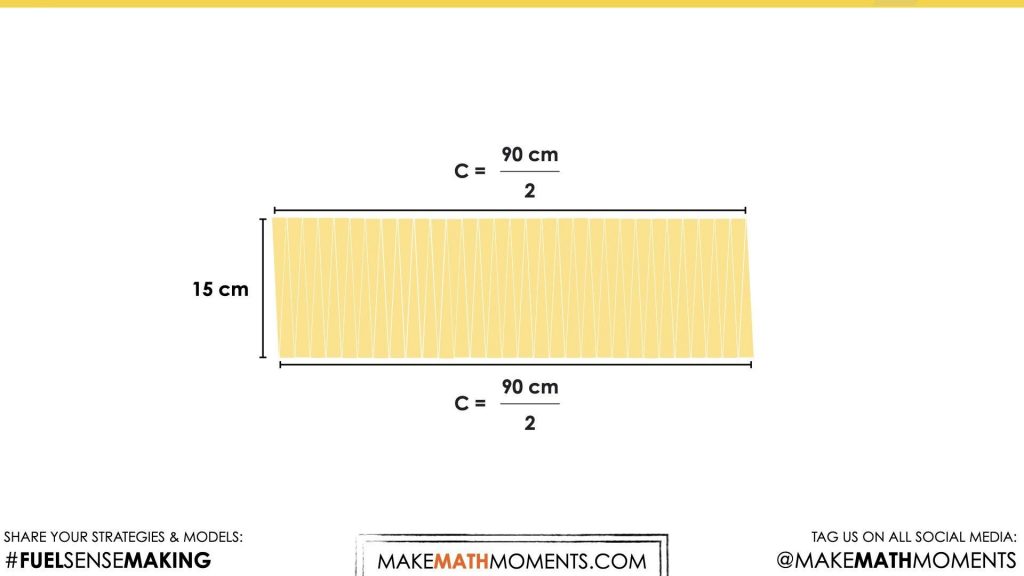
With this, we hope that students are able to visualize (or draw) that the area of a circle can be found by decomposing the circle and recomposing into a parallelogram or rectangle as we explored in the Going In Circles unit. Through that unit, we learned that the width would be equivalent to the radius and the width would be equivalent to half of the circumference.
There may be some students who recall the formula for area of a circle as \(πr^2\) and that is completely fine as well. We still encourage those students to determine the result without the use of a calculator.
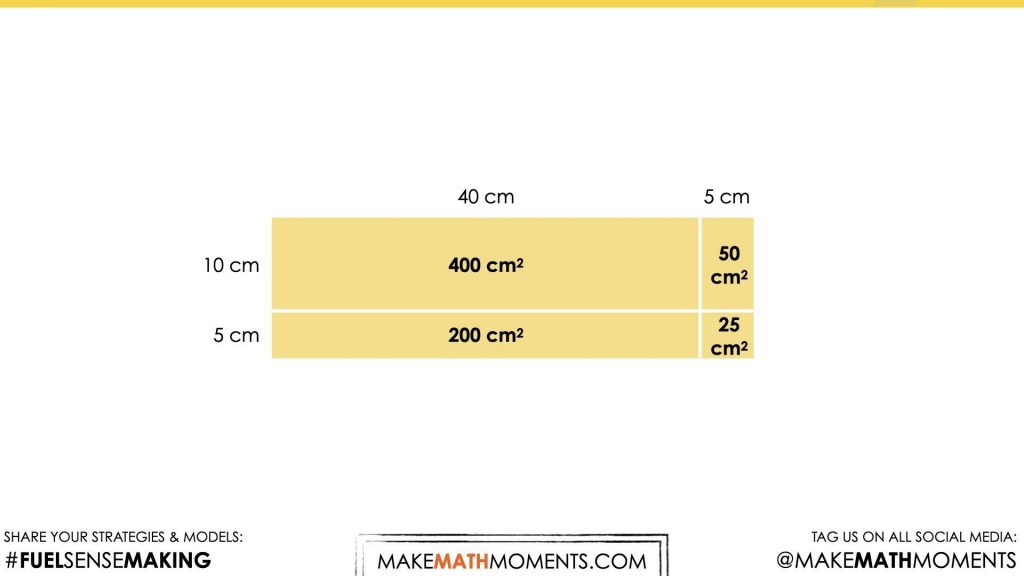
Regardless of which approach students take to solve for the area of the base, a common strategy you might see students use is partial products where the area of a rectangle is partitioned into two or more smaller product parts and then recomposed afterwards.
Visual Math Talk Prompt #1 serves as a means to recall prior knowledge regarding the area of a circle and hopes to emerge the idea that a cylinder with a height of only 1 unit simply transforms the number of ‘squares’ we calculated for the area into the same number of ‘cubes’.
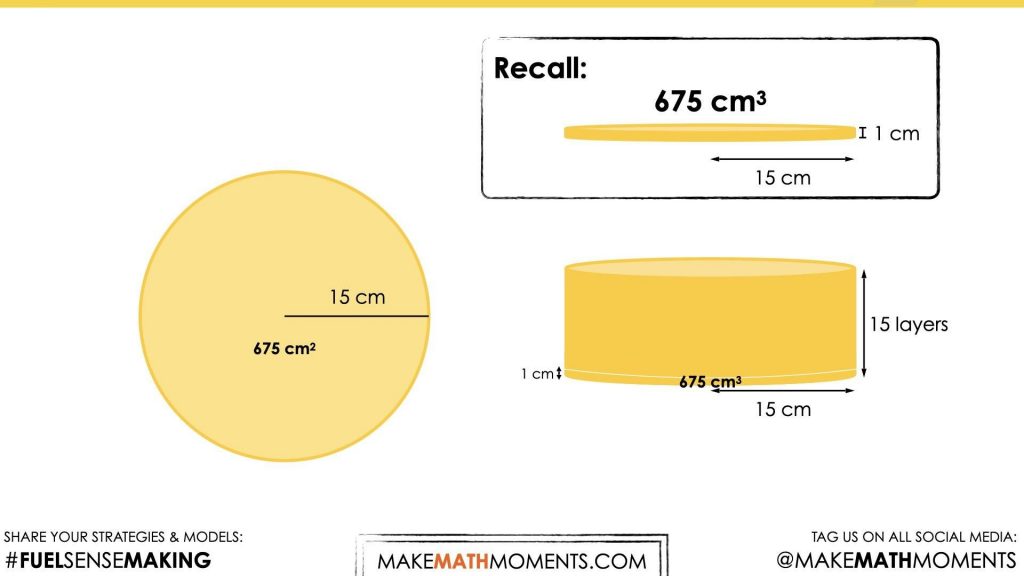
Therefore, the area of the base for this one layer cylinder is 675 square centimetres and has a volume of 675 cubic centimeters.
Visual Math Talk Prompt #2
Show students the following animation that builds on the previous, where the cylinder is then extended to a height of 15 cm (or 15 ‘layers’ of cubic centimetres):
Then ask students:
Without using a calculator, what might the approximate volume of this cylinder be?
With the image projected, give students 30 seconds to 1 minute to reflect on the question. Then students will do a quick turn and talk to share their thinking with a classmate.
After a reasonable amount of time, invite students to share their approximations.
Be sure to record student thinking in a space (eg., whiteboard) visible to all students. This honours the contributions of all students.
Some students may immediately recognize that this cylinder has the same base as the cylinder from the previous Visual Math Talk Prompt, however the height has increased from 1 cm to 15 cm tall.
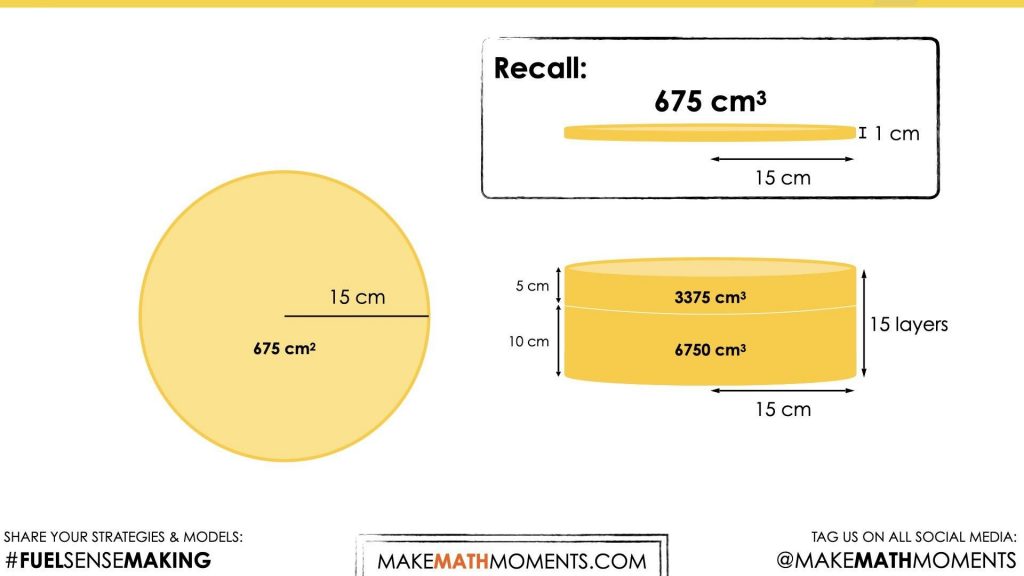
In other words, this cylinder has 15 times as many “layers” as the previous cylinder. Therefore, students who are additive thinkers can add 675 cubic centimeters repeatedly until they reach the 15th layer. Other students might choose to use a doubling strategy; doubling the volume of 1 layer to the volume of 2 layers; from 2 layers to 4 layers; 4 layers to 8 layers; and so on.
A worthwhile strategy to share and make connections to would be leveraging partial products where we determine the volume of say 10 layers and 5 layers before finding the sum.
It should be noted that different approximations used for the circumference and area of the base will impact the actual volume of the cylinder.
Visual Math Talk Prompt #3
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Visual Math Talk Prompt #4
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Spark Curiosity
A Night At The Movies
In this problem based lesson, we will be crafting a context involving a night at the movie theatre.
Consider using a script similar to the following while running the silent animation video:
You’re in the snack bar line at the movie theatre and you’re wondering which of the two sizes of popcorn you’d like to get. As you pull out your smartphone to use your calculator, you realize it is out of batteries.
What information might be useful to help you decide which size to get?
Give 30-60 seconds of individual ‘Think Time’ before offering students an opportunity to share their thinking with a classmate and then a whole group share.
While not completely necessary to record student thinking at this point, ideas shared by students can still be recorded in a space (eg., whiteboard) visible to all students.
Some student thinking that might emerge are:
- The cost of each container
- How long the line is
- I don’t want anymore popcorn
- And many more
Facilitator Note:
By scaffolding the learning in this way and being intentional with the questions/prompts provided for students, an authentic and meaningful opportunity is built in to foster increased student agency by involving all learners in the process of building the problem. While acknowledging all ideas honours the thinking of all students, what is being worked towards is the minimal amount of information needed to begin working through the problem.
Estimation: Prompt
Now that students have had an opportunity to share their thinking regarding what information might be useful, prompt students with:
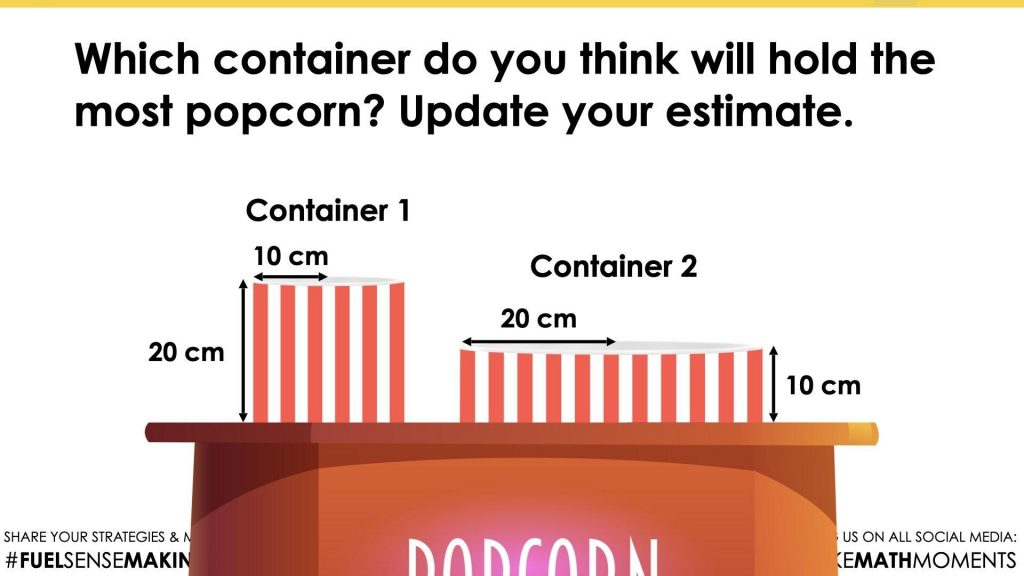
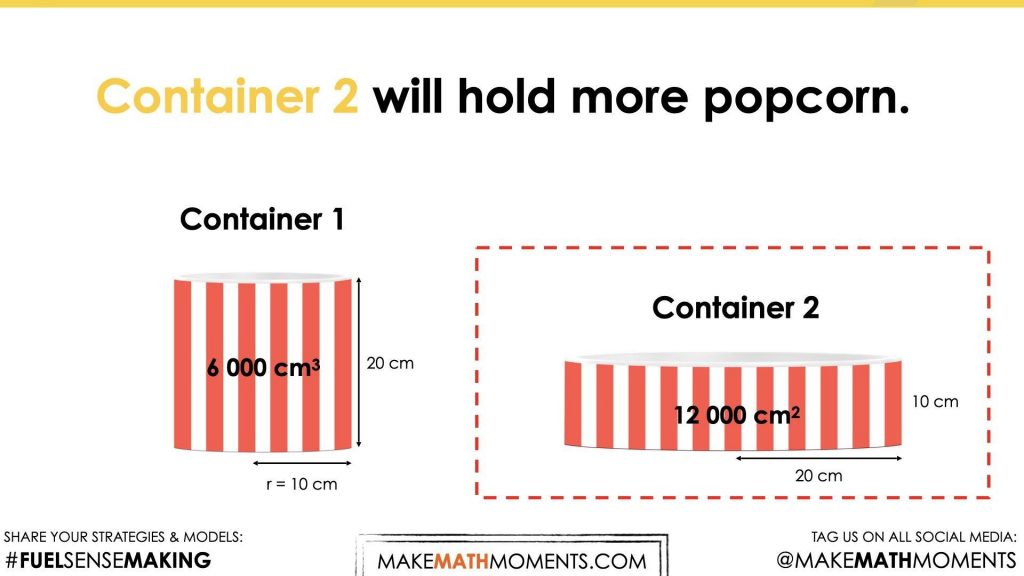
Which container do you think will hold the most popcorn?
Make an estimate.
It is worth noting that both containers are in fact cylinders.
Allow students to share their estimates with neighbours and then out to the class.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Prompt students to update their estimates given the following information:
Which container do you think will hold the most popcorn?
Update your estimate.
Encourage students to come up with an argument, however without the use of a calculator. Their solution might not be extremely precise, however their calculations should support their argument for which container will hold more popcorn.
Next Moves
Consolidation
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Purposeful Practice
While Students Are Practicing…
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Questions: Calculating the Volume of a Cylinder
Allow students the opportunity to engage in purposeful practice without the use of a calculator to promote their fluency and flexibility with these concepts and to model their thinking:
Question #1:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #2:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #3:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #4:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #5:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Resources & Downloads
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!