GOING IN CIRCLES
EXPLORING PI: CIRCUMFERENCE & AREA OF CIRCLES
Leverage contextual problems to investigate and emerge Pi to help conceptualize formulas for both the circumference and area of a circle.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 8 Days
Access each lesson from this unit using the navigation links below
Students will use spatial reasoning to first estimate and then investigate the relationship between the circumference and the diameter of a circle in order to determine which is longer: the circumference or the height of a drinking glass.
In this task, students will explore the concept of circumference through estimation followed by measurement. This task will allow students to develop a deeper understanding of big ideas, including the following:
- When exploring measurement relationships of any circle, there are three (3) standard measures that can be used to reveal more information about the circle:
- Circumference: the perimeter of a circle.
- Diameter: any straight line segment beginning and ending on the outer edge of a circle and passes through its centre.
- Radius: any straight line segment beginning at the centre of a circle and ending on the outer edge of the circle.
- Knowing one of the standard measures of a circle provides information about all other measures;
- There is a multiplicative relationship between the length of the diameter and the circumference of a circle. In other words, as the diameter of a circle increases, the circumference increases multiplicatively (not additively);
- For all circles, the ratio of the circumference to the diameter is the same (approximately 22:7); and,
- For all circles, the rate of each unit of circumference length per unit of diameter length is the same (approximately 22/7 or 3.14) and is known as Pi, π.
Note:
There are some very complex mathematical understandings happening “under the hood” when we explore the differences between ratios, rates, and other nuances along the journey through proportional relationships. If you want to build your mathematical content knowledge to assist in better understanding the progression through comparison, additive thinking, multiplicative thinking, ratios, rates, and proportional relationships, consider joining us in our 9-module self-paced course called The Concept Holding Your Students Back.
Lesson Walkthrough Video
Watch the following video that gives you a sneak peek into a virtual classroom where this lesson is being delivered via online learning:
Note that for privacy reasons, you cannot see student names or hear their voices, but you can get a sense as to how you might facilitate this lesson in a virtual environment and extrapolate to how this could look/sound in a face-to-face classroom environment.
What You’ll Need…
- Various cylinders (glasses, water bottles, etc.) for measuring
- on-standard measuring tools (i.e.: string, paper strips, the cord from earbuds, etc.)
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Replaying the video and/or leaving a screenshot from the video up can be helpful here.
Then, ask students to share with their neighbours for another 60 seconds.
Consider sharing the following video to give them a closer look at the glass itself:
Finally, allow students to share with the entire group. Be sure to write down these noticings and wonderings on the blackboard/whiteboard, chart paper, or some other means to ensure students know that their voice is acknowledged and appreciated.
Some of the noticing and wondering that may come up includes:
- I notice a clean kitchen.
- I notice a glass.
- I notice string.
- I wonder why there is a string on the counter?
- I wonder if you will be using the string to wrap around the glass?
- I wonder if the person is about to pour a drink?
At this point, you can answer any wonders that you can cross off the list right away and of course, you can create your own answers for some of these wonders as you leverage your storytelling skills. For example:
- You could explain who the person is (is it you? a friend? a family member?)
- You could explain what kind of drink they were planning to have (orange juice? water?)
- You could start explaining what was going through your mind as the glass was placed on the countertop and mention that someone once asked you about which was longer: the distance around the top of the glass (circumference) or the height.
- And so on…
Spending times to acknowledge and address specific thoughts that students shared whether a notice or a wonder is crucial to building a culture in your classroom where students know that their voice is being valued and thus encourages them to continue sharing their thoughts and opinions later in this lesson and in future lessons.
Estimation: Prompt
After we have heard students and demonstrated that we value their voice, we can land on the first question we will challenge them with:
Which is longer: the distance around the top of the glass or the height of the glass?
Make an estimate.
Be sure to clarify that we will be exploring the distance (circumference) around the top of the glass where it appears to be widest.
Be sure not to skip over asking students to make an estimate using only their spatial reasoning skills as this is a very important step in the Curiosity Path. Providing students an opportunity to make an estimate and try to articulate their thinking with their peers provides a very low floor opportunity for them to not only better understand the context, but to also begin nudging them to think about what will be important to make their estimate more precise as we continue through the lesson.
Investigation
Provide students (or ask students to gather) cylindrical objects for them to explore with the intent of updating their original estimate with a more precise estimate.
Prompt students to:
Explore various glasses and/or cylindrical objects and compare the circumference of a base from these cylinders to its height using a non-standard measuring tool (i.e.: string, paper strip, etc.).
Record your results.
Are the results what you expected? Were there any surprises?
Record these reflections as well.
Facilitator Notes:
Some students may be surprised by the results they observe when comparing the circumference of a base of a cylinder to its height. For cylinders that appear to be much taller than its width, in some cases the circumference is still longer.
Other students may not notice much of anything, which is an important observation the facilitator can use to help assess how far along the continuum of comparison they might be.
Are students struggling to make a non-standard measured comparison to see that one length is longer or shorter than the other? Are students making additive comparisons (the circumference is a little longer than) or multiplicative comparisons (the circumference is about 1 and 1 fourth times as long as)?
Investigation Share Out & Update Estimates
Give students the opportunity to share out their findings from their investigation with their neighbours.
Walk amongst the groups to listen and observe their discussions so you can be intentional about how you select and sequence those who share and in what order. For example, giving students who haven’t necessarily landed on a firm conclusion first to share their current thinking is helpful to allow them to have a voice in this discussion.
Work your way to other students who may have noticed the surprise that in many cases, the circumference of the base of some cylinders was longer than the height even when the cylinder was much taller than wider.
After students have shared their thinking, give them time to revise their estimates based on what they observed and recorded from the investigation compared to the glass they see in the video.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Show students this short silent animation clip to reveal more information about the glass:
Prompt students by stating:
Which is longer: the circumference or the height?
Update your estimate.
You can also extend this prompt by asking:
About how much longer?
Convince your math community.
The intent here is to promote the idea of students estimating more precisely through a measured comparison using squares as a unit or count.
Facilitator Note:
Without providing students with a few purposeful questions, it is unlikely that many students will hypothesize that there is a relationship between the 8 square long diameter of the glass and the circumference. Thus, you will want to prompt students to go back to the cylinders they had already investigated to determine if there is some sort of relationship between the diameter and circumference.
A prompt such as:
The distance across the circle through the centre (the diameter) is 8 squares long.
Do you think this might be able to help us determine the circumference around the circle?
Revisit some of the cylinders you investigated to see if you notice a relationship that might be helpful.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse.
After students have shared out their updated estimates based on what they learned from the investigation, it is unlikely that students would have noticed a relationship between the circumference and diameter of the circular opening of each glass since they are likely focusing more on whether there is a relationship between the circumference and the height of each glass.
Attempt posing purposeful questions that may help draw some attention to the relationship between the Circumference and the diameter of each cylinder.
Consider prompts such as:
What do you notice about the length of the Circumference of each cylinder? Is longer or shorter than you expected?
And/or:
I notice that you’re comparing the Circumference of each cylinder to the height, which is great! I wonder if there are any other attributes you could measure on the cylinder to see if you notice any other interesting relationships?
And/or:
Which cylinders (point towards the different cylinders the student is working with) do you think have the longest Circumference?
(Wait for response)
Why do you suppose that is?
This particular prompt hopefully assists some students in focusing their attention towards what other attributes are getting larger/smaller as the Circumference of each cylinder gets larger/smaller.
Some students might notice that the area of the base gets larger as the Circumference gets larger. Celebrate this notice. Asking them what else gets larger may help some students land on the fact that the wider the cylinder, the longer the Circumference.
If we can help to emerge this relationship through purposeful questioning rather than simply stating, this will make for a more sticky learning opportunity for each student.
Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Concrete non-standard measuring tools like string, paper measuring strip, etc.;
- Connecting cubes iterated around the circumference and then “stacked” to compare to the height;
- Charts and tables; and,
- many others…
Have students share their strategies and reasoning based on what they found from investigating various cylinders and comparing the length of the diameter to the circumference.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Facilitator Note:
Even with carefully crafting purposeful questions such as those listed above, this exploration may not lead to students discovering the relationship between circumference and diameter.
Do not panic if students do not come to this conclusion, but rather celebrate their strategies for how they arrive at their conclusion of whether the Circumference or the height of the glass in the video will be longer.
Have students share their strategies and reasoning for determining whether the glass will have a longer circumference or longer height. Ask them to convince you and their peers that their answer is correct by sharing mathematical reasoning.
Student Approaches
Student Approach #1: Comparing Cylinders
The circumference is going to be a lot longer than the height because even on this tall and thin cup (holding the tall and thin cup), the circumference was about the same as the height.
The cup in the video looks shorter and wider than this cup.
Student Approach #2: Recognizing Circumference to Diameter Relationship
After you (the teacher) asked me about what other attributes I could measure to try and discover more relationships I noticed that the Circumference was definitely longer on wider cups than on thinner cups (holding a wide cup and thin cup and comparing their bases).
When I used my measuring strip to measure the length of the Circumference and diameter and compare them, I noticed that the Circumference was about 3 times as long as the diameter on both.
The height of the cup in the video doesn’t look longer than 3 times of the diameter, so I think the Circumference will be longer.
Student Approach #3: Understanding Circumference to Diameter Ratio, or π
When sharing the height of glass (14 and 1 half squares) and diameter (8 squares), expect some students who have already been exposed to the ratio relationship between the length of the Circumference and the diameter may come to a conclusion such as:
Since it takes a bit more than the length of the diameter 3 times to get around the circumference of the glass and tripling 8 squares is 24 squares, we know the circumference will be longer.
Celebrate this reasoning and nudge the student to continue their learning by asking the student to become more precise with this estimate and/or to find how much longer the circumference is.
Student Approach #4: Understanding π and Applying Circumference Formula
Other students who have experience working with Circumference of a circle may be able to apply the formula either through reasoning and/or symbolically.
A student who uses reasoning might say:
Since the circumference is about 3 and 14 hundredths times as long as the diameter, tripling 8 squares is 24 squares. Then, 1 fourth of 8 squares is 2 squares, which is the same as 25 hundredths. Half of 25 hundredths is 12 and 1 half hundredths which is almost 14 hundredths, so I can half 2 squares to get 1 square. In total, I’d say the circumference is about 25 squares long.
A student who has experience using the formula symbolically might show:
C = πd
= (3.14)(8 squares)
= 25 squares approximately
Since the height is only 14 squares long, then the circumference is about 11 squares longer than the height.
Next Moves
Consolidation
During the consolidation, be sure to gather student work samples or make note of student approaches while you were monitoring as students work productively struggling.
Facilitate a discussion by referencing some of the student approaches including their strategies, tools and representations.
If a/some students noticed that there was a relationship between the length of the Circumference and the length of the diameter (whether it was on their own or from your purposeful questioning), be sure to ask one of those students to share their discovery with the group.
If students have not noticed something about the circumference and diameter is “interesting” or developing some sort of pattern, then you should use two (or more) of the cylinders with different diameters to now directly prompt students to consider the length of the Circumference and diameter of each. Something like:
Look at the base of both of these cylinders. Visualize the length of each diameter and the length of each Circumference. What do you notice? Can you make any claims or conjectures?
Many students will notice that the Circumference and the diameter is longer on the “wider” cylinder and both measures on the “thinner” cylinder are shorter.
Ask students if they notice anything consistent about the relationship between the circumference and the diameter. Possibly even have a volunteer measure both the diameter and Circumference of both cylinders to compare them.
Some students might get stuck thinking additively where they see that a circle with a diameter of say 5 cm has a circumference of about 15 cm and thus the circumference is about 10 cm bigger.
Be sure to help students think multiplicatively by noticing that a circle with a diameter of 5 cm has a circumference that is just about “3 times as big as”.
Have students check this multiplicative relationship for all the openings of each glass and they should come to the conclusion that the circumference of each opening is about 3 diameters in length or 3 times as big as the diameter.
We can now name this relationship that we’ve noticed as the ratio of the length of the Circumference to diameter as Pi, π.
Consider sharing the following silent solution animation video to visually show how just over 3 copies of the diameter are needed to “wrap” the perimeter of the top of the glass:
Here’s a screenshot of the final frame:
Note that you can also push students to leverage their prior knowledge of equivalent fractions to determine the difference between the length of the circumference and the height of the glass:
Promoting students utilizing their understanding of equivalence and fractions is important to allow them to continue building fluency with number and in particular, comparing and operating with fractions.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
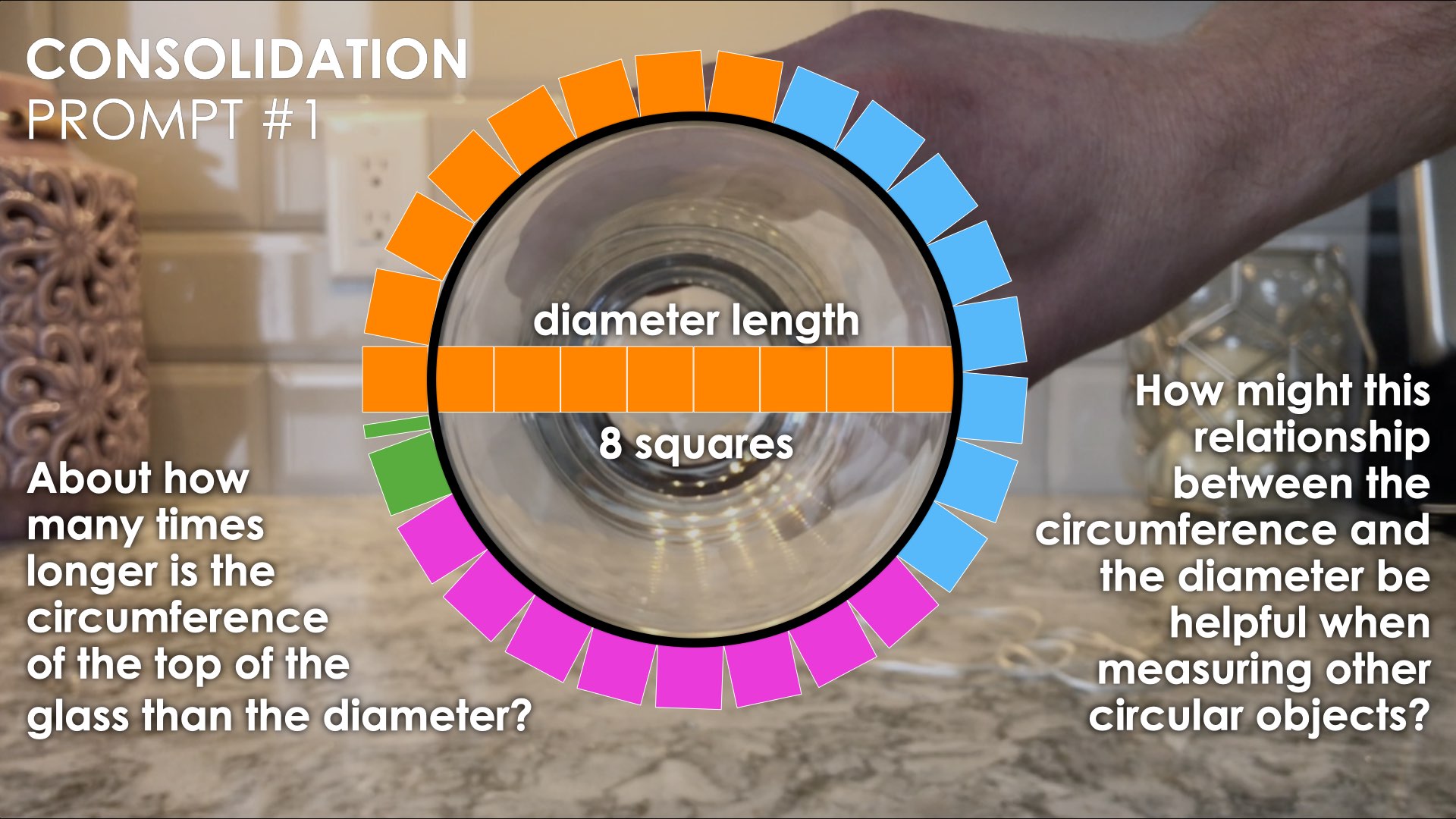
Consolidation Prompt #1:
About how many times longer is the circumference of the top of the glass than the diameter?
How might this relationship between the circumference and the diameter be helpful when measuring other circular objects?
After students share out the next day, you could share the following reveal video that reiterates the multiplicative relationship between the circumference and the diameter of a circle.
Here’s a screenshot of the final frame:
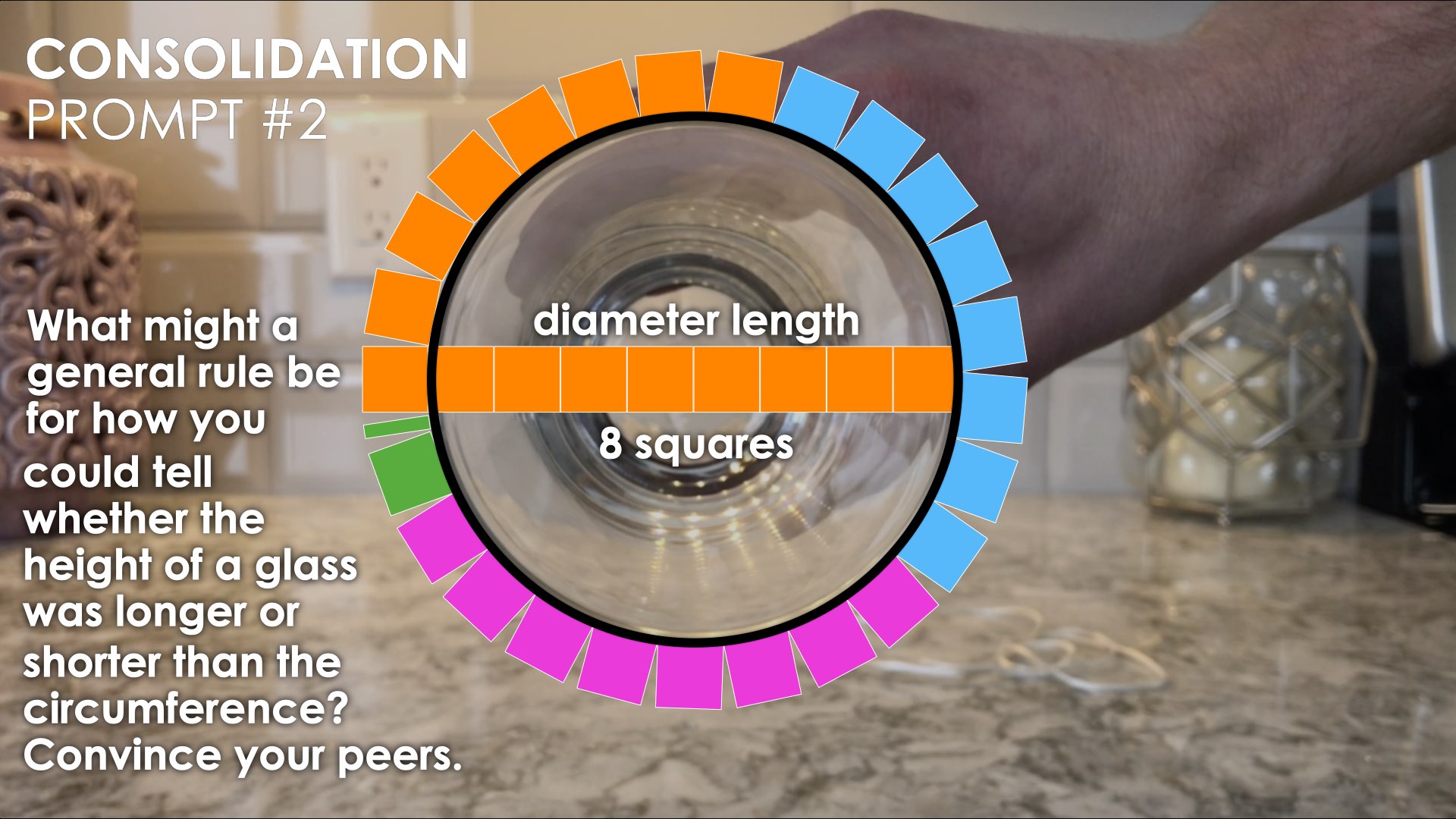
Consolidation Prompt #2:
What might a general rule be for how you could tell whether the height of a glass was longer or shorter than the circumference?
Convince your peers.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!