PLANTING FLOWERS REVISITED [DAY 5]
TWO-STEP ALGEBRAIC EQUATIONS
Dive into this Unit of problem based 3 Act Math Talk lessons focused on contextualizing and solving two-step algebraic equations.
Intentionality
Math Talk
Visual Math Talk Prompt #1
Visual Math Talk Prompt #2
Visual Math Talk Prompt #3
Visual Math Talk Prompt #4
Assessment
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will demonstrate the concepts and skills that they have developed through this context and learning experience.
Intentionality…
The purpose of this assessment is for students to demonstrate their understanding of the following big ideas.
- There are two types of division;
- Quotative division is when the total quota is known (the dividend), and the number per group or the rate (the divisor) is known;
- Quotative division reveals the number of copies or iterations of a rate that can be derived from the overall quota (the dividend);
- In quotative division, the dividend and the divisor have the same unit;
- Partitive division is when the total quota is known (the dividend), and the number of parts or groups (the divisor) is known;
- Partitive division reveals a rate;
- In partitive division, the dividend and the divisor often have different units;
- The dividend from any division sentence can be decomposed into smaller parts to allow for friendlier division by the divisor. This strategy is known as partial quotients. (i.e.: 85 ÷ 5 = 45 ÷ 5 + 40 ÷ 5 = 9 + 8 = 17);
- Division is the inverse operation of multiplication;
- Subtraction is the inverse operation of addition;
- Variables are used to represent changing or unknown quantities;
- When solving an equation where the coefficient of the unknown variable is not equal to 1, division is required to determine the value of the unknown variable and the context of the problem determines which type of division is required.
- A two-step equation is an algebraic equation that takes you two steps to solve.
The independent assessment will allow students to demonstrate concepts and skills related to the following learning goals:
- I will demonstrate an understanding of both partitive and quotative division.
- I will demonstrate an understanding of the inverse relationship between multiplication and division.
- I will demonstrate an understanding of the inverse relationship between addition and subtraction.
- I will demonstrate an understanding of the use of a variable in a two-step algebraic equation.
- I will model both partitive and quotative division.
- I will model and solve two-step algebraic equations that involve multiplication, addition and subtraction.
Students might write and/or model their answers independently. Students can also be interviewed by their teacher.
An alternative assessment opportunity should be offered if this tool will not successfully capture what the student knows, understands or can do.
Math Talk
In today’s math talk, students will use an appropriate model to solve the following one-step algebraic equations eliciting both partitive and quotative division. Encourage students to name the type of division required to solve and to create a context for each equation. Students are encouraged to use a model to solve and/or communicate their thinking.
m(8) + 7 = 39
6(p) + 5 = 35
b(9) – 4 = 95
7(p) – 8 = 34
Although you could lead this math talk by orally sharing the context and representing student thinking on a chalkboard/whiteboard, consider leveraging the following visual math talk prompt videos to ensure accessibility for all students. We would recommend that you still model student thinking to ensure student voice is honoured prior to sharing the visual silent solution shared in the visual prompt video.
Visual Math Talk Prompt #1
Show the following visual math talk prompt and be ready to pause the video once prompted:
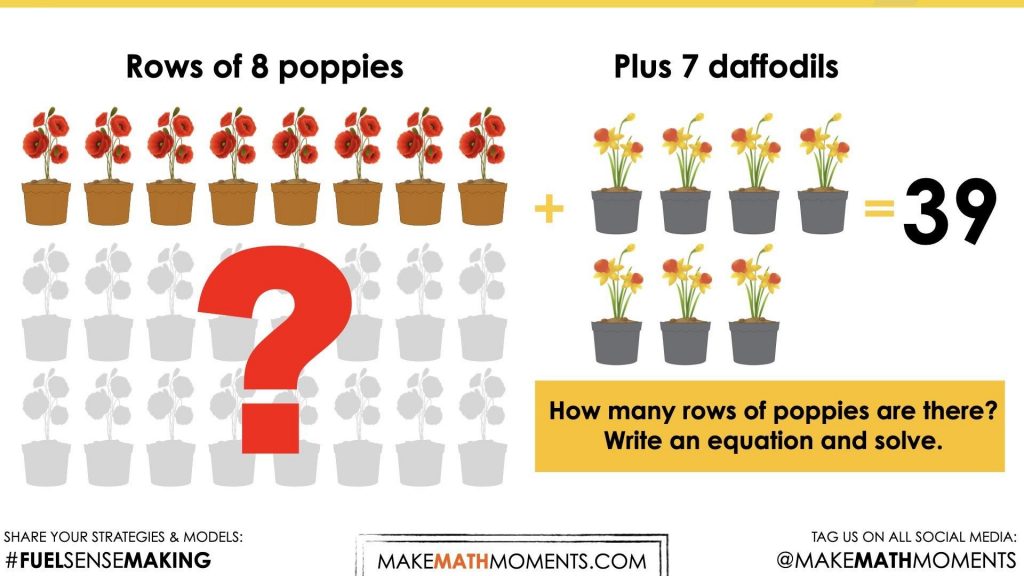
In the video, students are presented with visuals and a text prompt to set the context involving rows of poppies (a type of plant) and daffodils (another type of plant). The context might sound something like this:
Rows of 8 poppies are planted in the garden.
An additional 7 daffodils are planted nearby.
There are 39 plants in total.
How many rows of poppies are there?
Write an equation and solve.
The equation we hope students land on is:
m(8) + 7 = 39
Note that we have used a non-traditional format for this equation because we are trying to be intentional about m representing the number of groups or rows of poppies to help students realize that this means we are dealing with a quotative division situation.
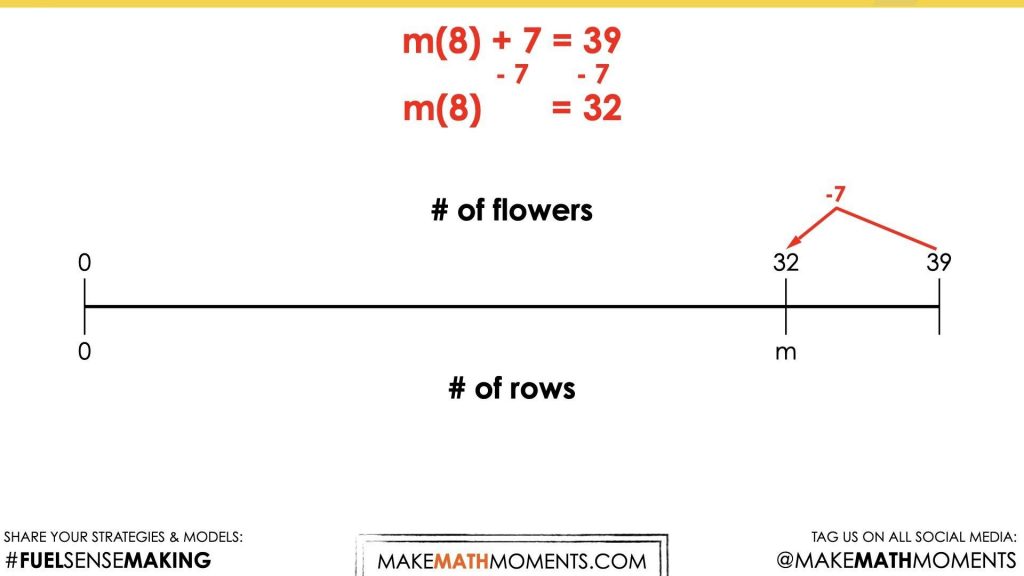
Before we can get to dividing quotatively, we must first take care of the extra daffodil plants that have increased the quantity to 39 plants in total.
We can do this by subtracting the 7 daffodils on both sides of the equation.
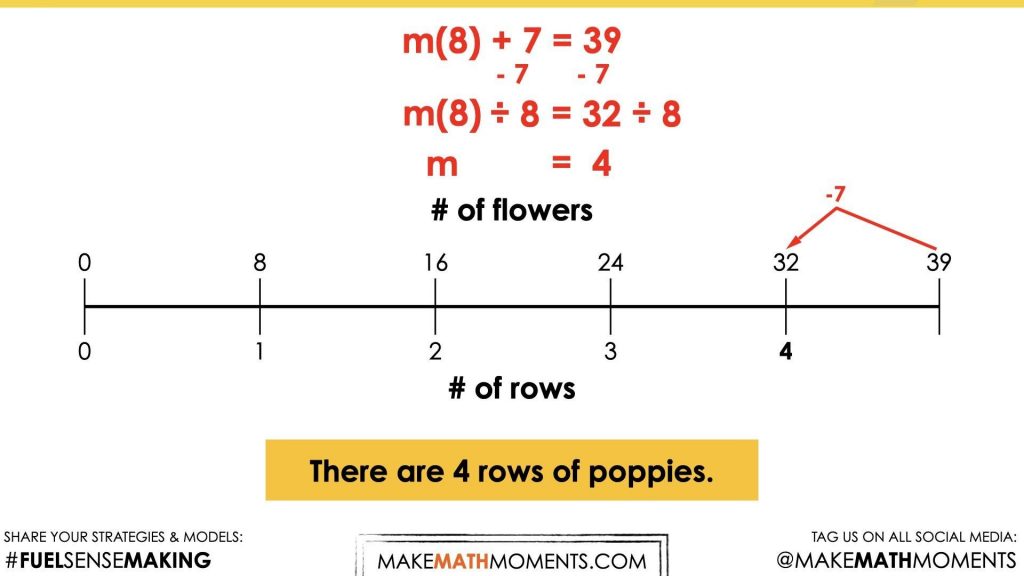
This leaves us with 32 poppy plants and a rate of 8 poppy plants per row. From here, we can leverage quotative division to determine the number of rows of poppy plants there must be.
Although you must do your best to model student thinking and honour their voice, ask the student if you can show their thinking on a linear model or ask them if they can “see” their thinking on the double number line to promote the use of this powerful model.
Visual Math Talk Prompt #2
In the second math talk prompt, we’ll give students a similar context, but this time we will not give them the visual to work with.
A context such as:
6 rows of poppies are planted in the garden.
An additional 5 tulips are planted nearby.
There are 35 plants in total.
How many poppies are there in each row?
Write an equation and solve.
The equation we are hoping students will land on is:
6(p) + 5 = 35
We also hope that through this process we can be clear that the unknown we are hoping to solve for in this situation is different than in the first. In this case, we know the number of rows (or groups), but we would like to determine the number of poppy plants in each row/group (the rate).
This means the type of division we will be using in the last step of solving this two-step equation will be partitive since we are dividing to reveal the rate.
Visual Math Talk Prompt #3
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Visual Math Talk Prompt #4
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Assessment
Assessment Considerations…
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Assessment: Solving Two-Step Algebraic Equations
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!