PLANTING FLOWERS REVISITED [DAY 2]
TWO-STEP ALGEBRAIC EQUATIONS
Dive into this Unit of problem based 3 Act Math Talk lessons focused on contextualizing and solving two-step algebraic equations.
Intentionality
Math Talk
Visual Math Talk Prompt #1
Visual Math Talk Prompt #2
Visual Math Talk Prompt #3
Visual Math Talk Prompt #4
Visual Math Talk Prompt #5
Visual Math Talk Prompt #6
Purposeful Practice
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will explore modelling and solving two-step algebraic equations involving multiplication and division.
Intentionality…
The purpose of the Day 2 activities is to reinforce key concepts from Day 1. Students will engage in a string of related problems through a math talk and will have an opportunity to complete independent purposeful practice. The math talk and purposeful practice serve to develop a deeper understanding of the following big ideas.
- There are two types of division.
- Quotative division is when the total quota is known (the dividend), and the number per group or the rate (the divisor) is known.
- Quotative division reveals the number of copies or iterations of a rate that can be derived from the overall quota (the dividend).
- In quotative division, the dividend and the divisor have the same unit.
- The dividend from any division sentence can be decomposed into smaller parts to allow for friendlier division by the divisor. This strategy is known as partial quotients. (i.e.: 85 ÷ 5 = 45 ÷ 5 + 40 ÷ 5 = 9 + 8 = 17).
- Division is the inverse operation of multiplication;
Variables are used to represent changing or unknown quantities. - When solving an equation where the coefficient of the unknown variable is not equal to 1, division is required to determine the value of the unknown variable and the context of the problem determines which type of division is required.
- A two-step equation is an algebraic equation that takes you two steps to solve.
Math Talk
Present the following equations one at a time. Encourage students to describe a context that could be represented by each. All of today’s equations and contexts should be quotative. Meaning, the rate is known, the number of groups is unknown.
For example:
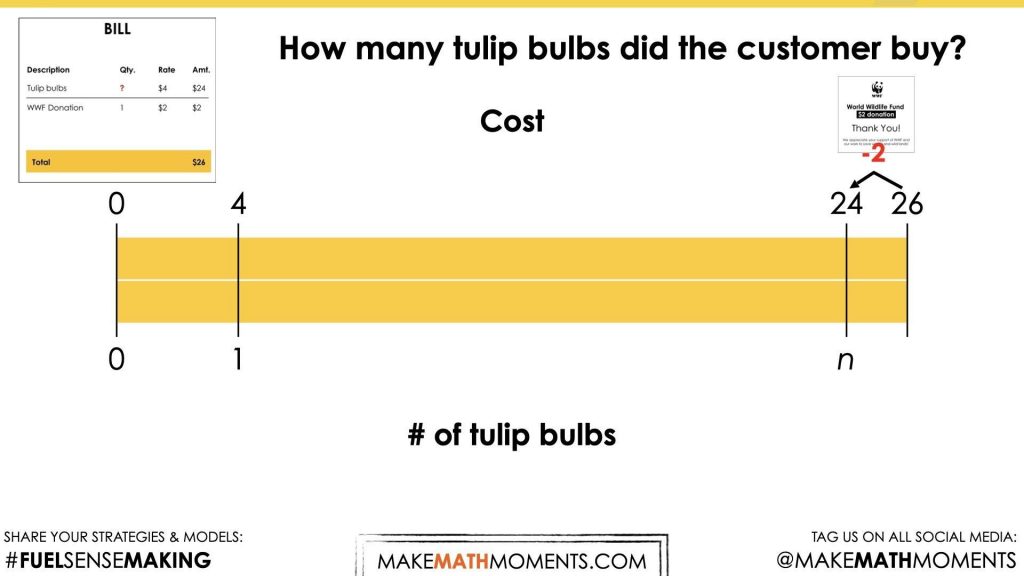
An unknown number of tulip bulbs at a cost of $4/tulip (the rate is known) were purchased, plus a two dollar donation was made to the World Wildlife Fund. If the total sale was $26, how many tulip bulbs did the customer buy?
Students should use a model of their choice to solve and/or represent their thinking.
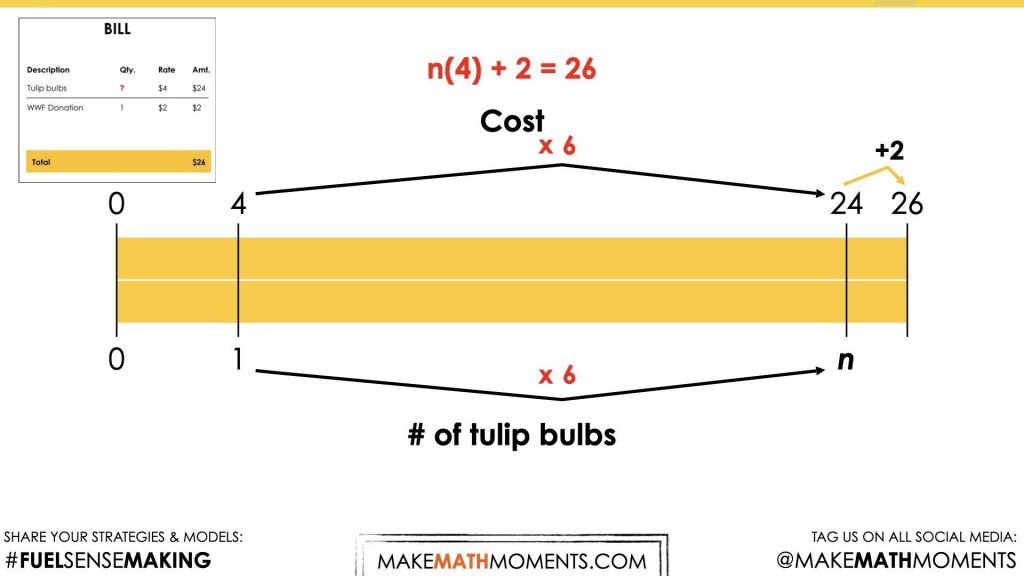
n(4) + 2 = 26
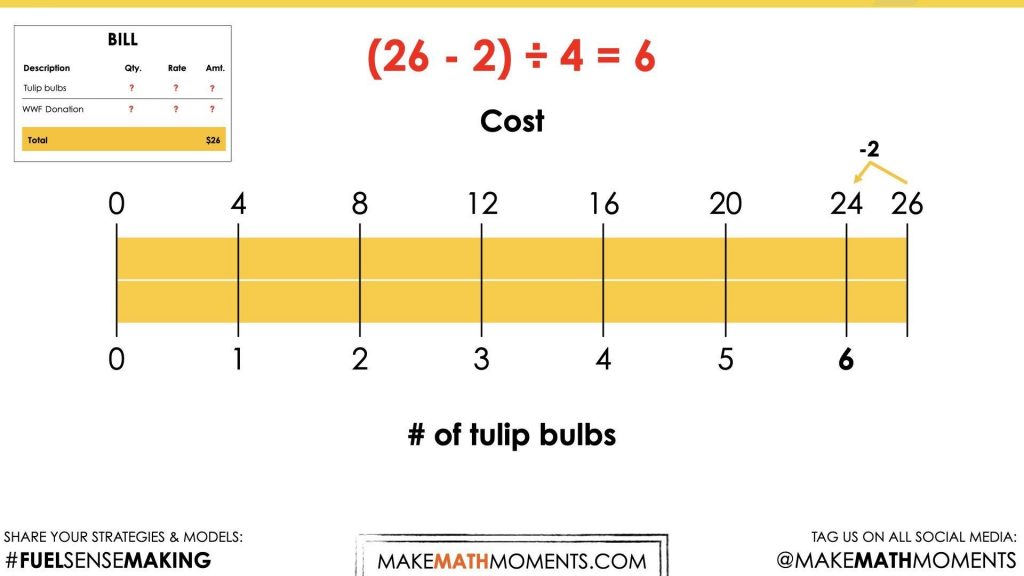
(26 – 2) ÷ 4 = n
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Consider leveraging the visual math talk prompt animations below to help you prepare to facilitate this math talk. The purpose of this math talk is to build fluency with solving two step equations requiring quotative division and to reveal that multiple equations can be written to represent one situation or context.
Visual Math Talk Prompt #1
Show the following visual math talk prompt and be ready to pause the video once prompted:
In the video, students are presented with visuals to set the context involving a purchase of tulip bulbs and a donation to the World Wildlife Fund (WWF).
The prompt is:
How many tulip bulbs did the customer buy?
While you could allow students to solve this problem utilizing the strategy and model of their choice, you might consider pushing students to also write an algebraic equation that could represent this problem. This is a teacher move that you will need to consider depending on the readiness of your group as to whether nudging in this direction is appropriate at this point or whether making the connection to the equation after solving is the better option.
Although students are free to leverage a strategy of their choosing, do your best to try and represent student thinking using a linear model like a stacked bar model (seen below) or a double number line. While the student may not have represented using this particular model, ensure that you are asking students for permission to represent their thinking in this way.
Consider using prompts like:
Is it alright if I represent your thinking this way?
And
Do you see your thinking represented on this stacked bar model?
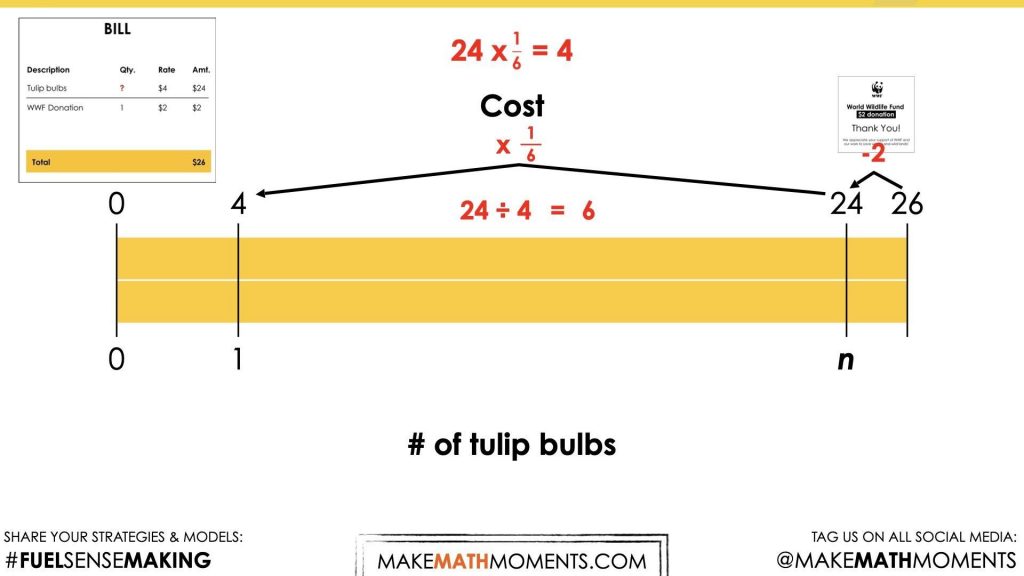
From this visual model, students may then be able to better understand and explain their thinking of how they solved for the number of tulip bulbs knowing that the rate was $4 per bulb.
Some students may choose to partition the rest of the stacked bar model by starting at $4 to 1 tulip bulb and skip count by that ratio of $4 to 1 bulb until they arrive at $24 and 6 tulip bulbs.
Others may immediately recognize that since the cost of the tulip bulbs was $24, we can quotatively divide $24 by $4 to reveal the scale factor of 6. Therefore, scaling 1 tulip bulb up by a factor of 6 will reveal 6 as the number of tulip bulbs purchased.
Showing the scale factor of 6 to scale up from $4 to 1 tulip bulb and the scale factor of 1 sixth to scale down from $24 to n tulip bulbs to $4 to 1 tulip bulb is an important relationship to explicitly highlight.
Finally, if students were not prompted to write an equation initially, be very intentional about prompting students to write an equation and make connections to the strategies and models shared to solve for the number of tulip bulbs purchased.
Visual Math Talk Prompt #2
Show the next visual math talk prompt and be ready to pause the video once prompted:
In this visual, we flip the script a bit here and rather than giving students enough information to solve the problem from the visuals, we share this prompt:
Use the context of cost and number of tulip bulbs to explain what the following equation might represent:
(26 – 2) ÷ 4 = n
You’ll notice that the only information shown in the images is the total cost of the bill which is $26.
At this point, we’re pushing students to engage in some sense making around the algebraic equation to hopefully allow them to reason through and realize that this algebraic equation is actually equivalent to the equation that was shared in the first prompt, n(4) + 2 = 26.
Although it might not be immediately obvious to students, this algebraic equation is actually modelling the use of opposite operations to solve the first equation, n(4) + 2 = 26.
For students who come to this realization quickly, be sure to nudge them to be convincing which means modelling this behaviour using a stacked bar model or other mathematical model of their choosing.
It is likely that students will leverage the model we shared in the first visual prompt as using it will mean that their “work” to explain and convince is already complete.
Visual Math Talk Prompt #3
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Visual Math Talk Prompt #4
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Visual Math Talk Prompt #5
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Visual Math Talk Prompt #6
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Purposeful Practice
While Students Are Practicing…
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Questions: Two-Step Algebraic Equations
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!