PLANTING FLOWERS REVISITED [Day 3]
TWO-STEP ALGEBRAIC EQUATIONS
Dive into this Unit of problem based 3 Act Math Talk lessons focused on contextualizing and solving two-step algebraic equations.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will determine how long in weeks that the sunflower has been planted in the garden.
Intentionality…
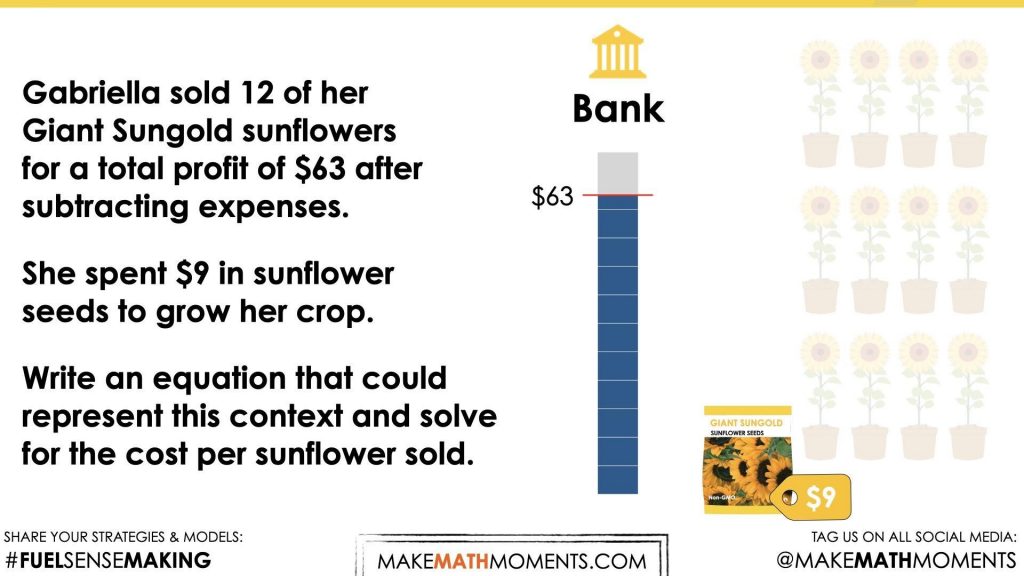
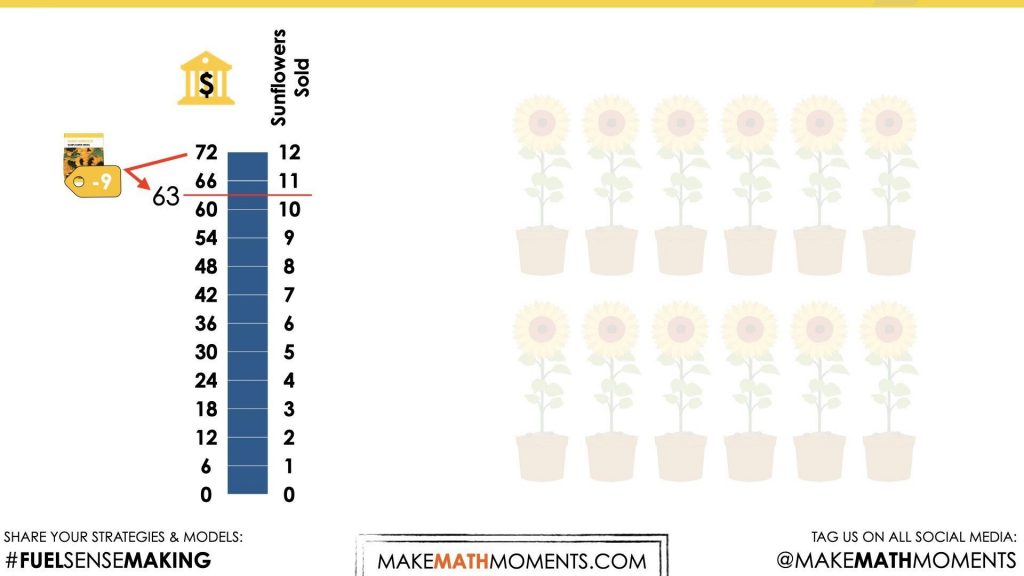
In this task, students will determine the price per sunflower. In this context, the total profit after startup costs have been withdrawn is known and the number of sunflowers sold. This context can be represented algebraically as a two-step equation. In order to solve, students will have to add the startup cost to determine the total sales, and then divide the total sales by twelve (the number of sunflowers sold). This context is partitive in nature.
Some of the big ideas that may emerge through this task include:
- There are two types of division.
- Partitive division is when the total quota is known (the dividend), and the number of parts or groups (the divisor) is known.
- Partitive division reveals a rate.
- In partitive division, the dividend and the divisor often have different units.
- The dividend from any division sentence can be decomposed into smaller parts to allow for friendlier division by the divisor. This strategy is known as partial quotients. (i.e.: 85 ÷ 5 = 45 ÷ 5 + 40 ÷ 5 = 9 + 8 = 17).
- Division is the inverse operation of multiplication;
Addition is the inverse operation of addition. - Variables are used to represent changing or unknown quantities.
- When solving an equation where the coefficient of the unknown variable is not equal to 1, division is required to determine the value of the unknown variable and the context of the problem determines which type of division is required.
- A two-step equation is an algebraic equation that takes you two steps to solve.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Replaying the video can be helpful here.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group. Be sure to write down these noticings and wonderings on the blackboard/whiteboard, chart paper, or some other means to ensure students know that their voice is acknowledged and appreciated.
Some of the noticing and wondering that may come up includes:
- I noticed twelve sunflowers.
- I wonder if these are Giant Sungold sunflowers like on Day 1.
- I wonder if they are being cut down.
- I wonder if Gabriella is selling the sunflowers.
- I notice the word bank on the screen.
- I notice the bank lost some money near the end.
I notice the bank is at $63. - I wonder how much each flower cost?
- I wonder why the metre went down at the end.
- And many more.
Estimation: Prompt
At this point, share the following information:
Gabriella has decided to sell some of her Giant Sungold sunflowers for a profit. After selling twelve sunflowers, she had made a total profit of $63 after subtracting the cost of buying the seedlings that she originally planted.
What was the price per sunflower that she charged each customer?
Make an estimate.
Consider what we already know and what we do not know.
Facilitator note: brainstorm these lists with students
What we know:
- There are 12 sunflowers.
- There is $63 in the bank after accounting for expenses
What we do not know:
- The cost of expenses
- The price per sunflower
Based on the bar model shared, students can use their spatial reasoning skills to estimate the number of dollars each individual unit represents.
Listen for students reasoning through this by starting with benchmark numbers like $10 per unit (or sunflower) and realizing that is too high since 12 groups of $10 is $120 and that is much higher than $63, whereas $5 feels more reasonable since half of $10 is $5 and half of $120 is $60.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Prompt students with the following:
Gabriella sold 12 of her Giant Sungold sunflowers for a total profit of $63 after subtracting expenses.
She spent $9 in sunflower seeds to grow her crop.
Write an equation that could represent this context and solve for the cost per sunflower sold.
Encourage students to use models and strategies that they feel comfortable and confident with, although nudging towards students making the connection between visual models and algebraic equations.
Consider what we already know:
Facilitator note: brainstorm this list with students
- There are 12 sunflowers.
- $9.00 was deducted from the total sales.
- There is $63 in the bank.
Consider what we do not know:
- The price per sunflower
Give students an opportunity to turn and talk. Ask students to share their ideas, strategies and models that will help them to both write an algebraic equation and solve for the cost per sunflower.
Be sure to remind students that they are not to use a calculator to determine the price per sunflower as using that tool will rob them of this mathematical experience. Students should use a mathematical model in order to communicate their thinking.
During Moves
While Students Are Productively Struggling…
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Student Approaches
Student Approach #1: Fair-sharing into twelve groups
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Student Approach #2: A linear model and partitioning
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Student Approach #3: An algorithm and known facts
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Next Moves
Consolidation
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering this consolidation prompt to be completed independently.
Consolidation Prompt #1:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Consolidation Prompt #2:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!