PLANTING FLOWERS REVISITED
TWO-STEP ALGEBRAIC EQUATIONS
Dive into this Unit of problem based 3 Act Math Talk lessons focused on contextualizing and solving two-step algebraic equations.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
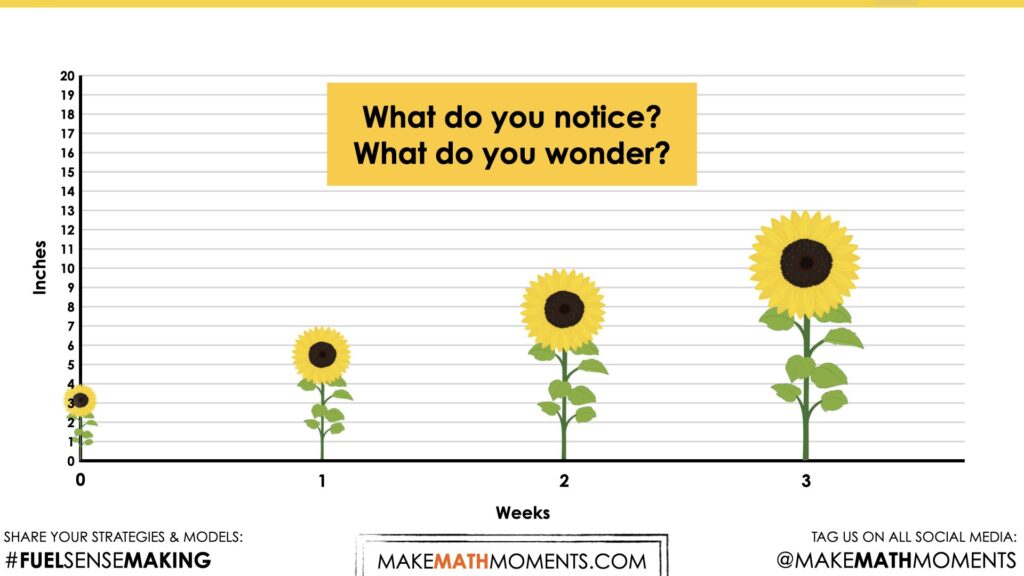
Students will determine how long in weeks that the sunflower has been planted in the garden.
Intentionality…
In this task, students will determine the total of weeks that the sunflower has been planted in Gabriella’s garden. In this context, the total height of the sunflower, the height when planted, and the rate (inches per week) is known. This context can be represented algebraically. In order to solve, students will have to remove the height when planted, and then use quotative division to determine the number of weeks. This context is quotative in nature.
Some of the big ideas that may emerge through this task include:
- There are two types of division;
- Quotative division is when the total quota is known (the dividend), and the number per group or the rate (the divisor) is known;
- Quotative division reveals the number of copies or iterations of a rate that can be derived from the overall quota (the dividend);
- In quotative division, the dividend and the divisor have the same unit;
- The dividend from any division sentence can be decomposed into smaller parts to allow for friendlier division by the divisor. This strategy is known as partial quotients. (i.e.: 85 ÷ 5 = 45 ÷ 5 + 40 ÷ 5 = 9 + 8 = 17);
- Division is the inverse operation of multiplication;
Variables are used to represent changing or unknown quantities; - When solving an equation where the coefficient of the unknown variable is not equal to 1, division is required to determine the value of the unknown variable and the context of the problem determines which type of division is required.
- A two-step equation is an algebraic equation that takes you two steps to solve.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Replaying the video can be helpful here.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group. Be sure to write down these noticings and wonderings on the blackboard/whiteboard, chart paper, or some other means to ensure students know that their voice is acknowledged and appreciated.
Some of the noticing and wondering that may come up includes:
- I noticed a sunflower.
- I noticed there is a scale on the right, it is going up by 1.
- I noticed the sunflower was 4 inches tall when it started.
- I noticed that every week it grew three inches.
- I wonder how tall it will grow.
- I wonder if it always grows at the same rate.
- And many more.
At this point, share the following information using the video animation and/or by telling a story verbally:
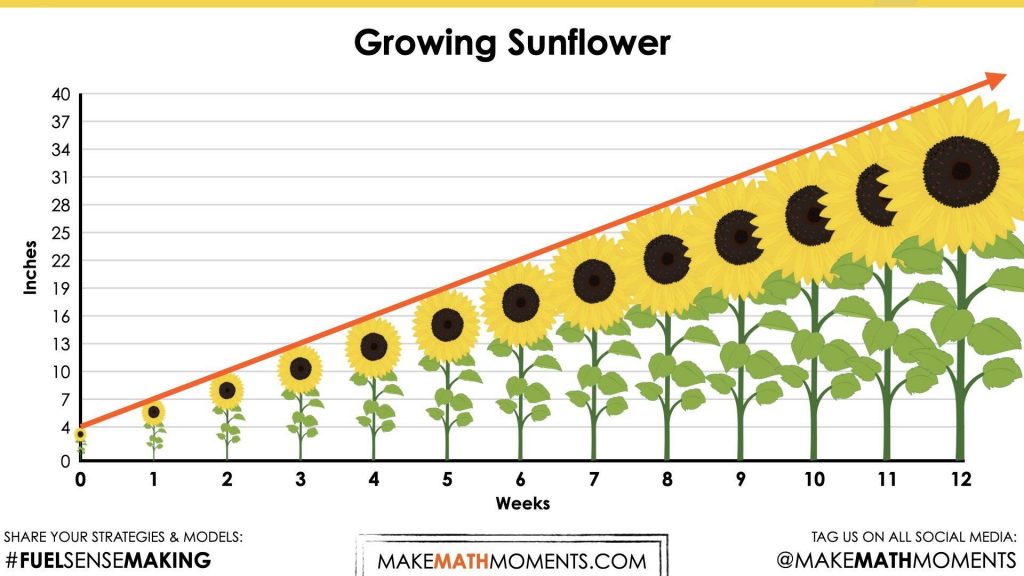
This sunflower was planted in Gabriella’s garden. It was four inches tall when she bought it. The farmer indicated that she should expect this variety of sunflower to grow an additional 3 inches every week until it reaches its maximum height in approximately 24 weeks.
Prediction: Prompt
Verbalize the following prompt and share it on the projector for students:
Based on the information provided, what variety of sunflower do you believe Gabriella planted? Justify your answer.
Skyscraper – average height: 144 inches
American Giant – average height: 120 inches
Giant Sungold – average height: 72 inches
We can now ask students to make a prediction (not a guess) as we want them to be as strategic as they can possibly be. This will force them to determine a variety of sunflower that would be reasonable based on the growing information provided by the farmer. Encourage students to share their predictions and justification.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Revisit what we already know about Gabriella’s sunflower.
This Giant Sungold sunflower was planted in Gabriella’s garden. It was four inches tall when she bought it. The farmer indicated that she should expect this variety of sunflower to grow an additional 3 inches every week until it reaches its maximum height in approximately 24 weeks.
Explain that this information can be represented as an algebraic expression to predict how tall Gabriella’s sunflower will be at the end of each week in her garden.
Student prompt #1:
Use the information about Gabriella’s sunflower to write an expression.
Ask students to share their expressions and discuss the similarities and differences that you find. We are ultimately going to land on the following expression:
w(3) + 4
Facilitator note:
In this expression, the variable represents the number of weeks. The three represents the rate (inches per week) and four is the height of the sunflower when it was planted.
You could also prompt students to write an equation:
H = w(3) + 4
Student prompt #2:
Gabriella’s sunflower is now 40 inches tall. How many weeks has it been planted?
This information can be represented as an equation.
w (3) + 4 = 40
Determine the number of weeks.
Be sure to remind students that they are not to use a calculator to determine the number of weeks as using that tool will rob them of this mathematical experience. Students should use a mathematical model in order to communicate their thinking.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Concrete to organize the inches into groups of three
- A concrete number line
- A bar model
- Partitioning a number line through partial products
- A division algorithm
Have students share their strategies and reasoning for how to represent the number of weeks. Ask them to convince you and their peers that their answer is correct by sharing mathematical models.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
Student Approach #1: Making Groups of Three
I grabbed 40 cubes, one for each inch. I took off 4 cubes right away, because the sunflower was 4 inches tall when she planted it. Then I made groups of three, each group represents one week. There are 12 groups, so twelve weeks.
Student Approach #2: A linear model and skip counting
I started counting by threes, three inches for every week. When I got to 36 inches, I knew that the last four inches were already there when she planted the sunflower. There were twelve jumps of three, so twelve weeks.
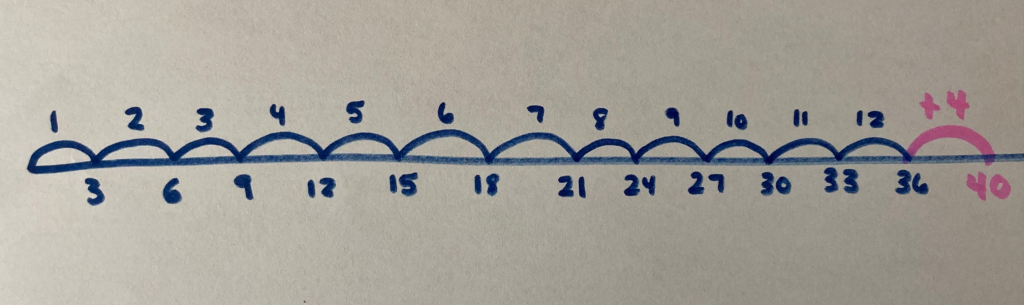
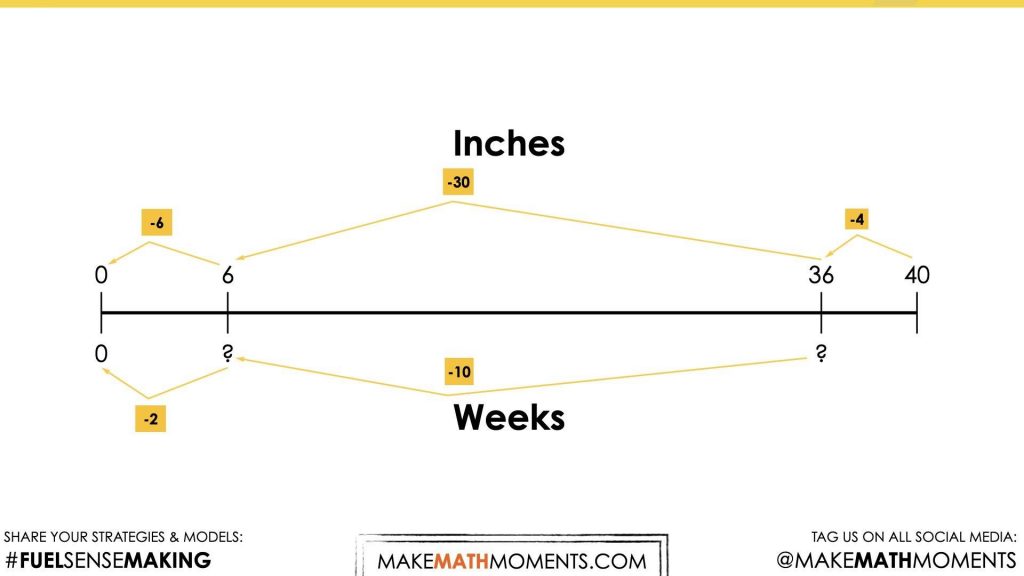
Student Approach #3: A number line and partial quotients
Right away, I took off four inches, the inches that were there when it was planted in the garden. I know that ten weeks would account for three inches, so I subtracted 30 from 36. with only 6 inches left, that’s another two weeks. Twelve weeks altogether.
Next Moves
Consolidation
You might consider selecting student solutions that move from making groups of three to skip counting or partial products.
You can see this model below:
Here are a couple screenshots highlighting a concrete model explicitly highlighting the skip counting in units of 3 inches:
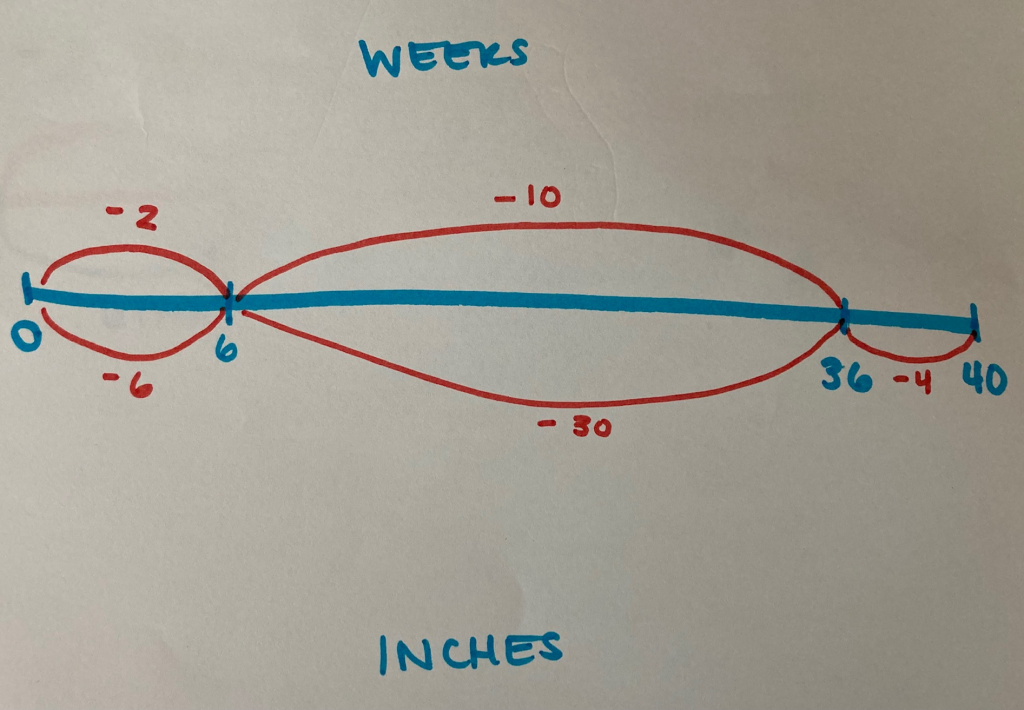
And this same thinking can be modelled on a double number line:
You might also consider sharing a strategy that leveraged inverse operations such as the solution video below.
In this representation, you can see the “undoing” of the equation by first subtracting 4 inches from 40 inches, then using quotative division to determine how many groups of 3 inches are in 36 inches:
Share the following equation to represent this strategy. Ask students to make a connection between the model and this symbolic representation. Encourage students to give each value within this equation a unit.
(40 – 4) ÷ 3 = 12
Compare this equation to our original equation.
w(3) + 4 = 40
What do you notice?
Hopefully students see that this equation is written backwards using inverse operations.
We solved a two-step algebraic equation, because it requires two steps to determine the value of the unknown quantity. The unknown number of weeks can be revealed by removing the starting height (4 inches), and dividing the total growth (36 inches) by the rate (3 inches/week), which is an example of quotative division.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering this consolidation prompt to be completed independently.
Consolidation Prompt #1:
Today we solve a two-step algebraic equation. Why was this equation considered two-steps?
Consolidation Prompt #2:
Consider the equation below. Write a context that could be represented by this equation. Model and solve.
w(5) + 4 = 59
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!