EVERGREEN
DATA AND FRACTIONS
Dive into this 5-day Problem Based Math Unit focused on displaying a data set of measurements in fractions of a unit.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview
Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will explore how to create a graphical representation of a categorical data set with measurements in fractions of a unit. Students will select an appropriate graph to display their data and justify their choice.
Intentionality…
In this task, students will investigate a data set that includes measurements in fractions of a unit. After planting a row of evergreens last Spring, the tree farmer goes out to record the growth of each tree, measured in feet. Students will be asked to display the height of all 10 trees using a graph of their choice. They will be asked to justify their choice of graph. Students will be asked to determine the difference in height between the tallest and shortest tree. Some of the big ideas that may emerge in today’s task include:
- There are different types of data;
- Categorical data refers to a data type that can be identified based on the names or labels given to them;
- Categorical data is either nominal or ordinal;
- Bar graphs are used to compare and contrast numbers, frequencies or other measures of distinct categories of data;
- The numerical values of a data set need to be considered when a scale is chosen;
- A fraction can represent a part of a whole;
- A structure of subtraction is comparison or difference.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Share the following video with students showing an evergreen tree appearing on the screen with a measuring stick next to it.
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group.
Some of the noticing and wondering that came up in a class recently included:
- I notice a tree.
- I notice a measuring stick.
- I notice the measuring stick is in feet.
- I notice the tree is between 2 and 3 feet tall.
- I wonder what kind of tree this is.
- I wonder exactly how tall the tree is.
- I wonder if this is a Christmas tree.
At this point, you can answer any notices and wonders that you can cross off the list right away.
Estimation: Prompt
Ask the following question:
What is the height of this tree? Be as precise as you can be with your estimate.
We can now ask students to make an estimate (not a guess) as we want them to be as strategic as they can possibly be. This will force them to use reasoning to try and come up with a reasonable fraction.
While Students Are Estimating…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Encourage students to use precise mathematical language and listen for the use of fractional language to describe the height of the tree.
Allow students to share their estimates with neighbours first, then with the class. Write down their estimates on the chalkboard/whiteboard/chart paper so students feel their voices are being heard and so they feel they have a stake in solving this problem.
A great way to build student understanding of the magnitude of number is to record their estimates on a number line for all to see. Another benefit of doing this is to see how estimates continually improve as we learn more and more information about the situation.
Estimation: Reveal
Share the following animation.
Celebrate students who estimated closest to a length of 2 and 3 fourth feet.
Fuel Sense-making
Crafting A Productive Struggle:
Since you have already taken some time to set the context for this problem and student curiosity is already sparked, we have them in a position to push their thinking further and fuel sense making.
Share the following silent animation.
Share the following story verbally to build the context of this problem with students:
Last spring, a tree farmer planted a row of 10 evergreen trees. The farmer went out to measure the height of each tree.
Share the following prompt with students:
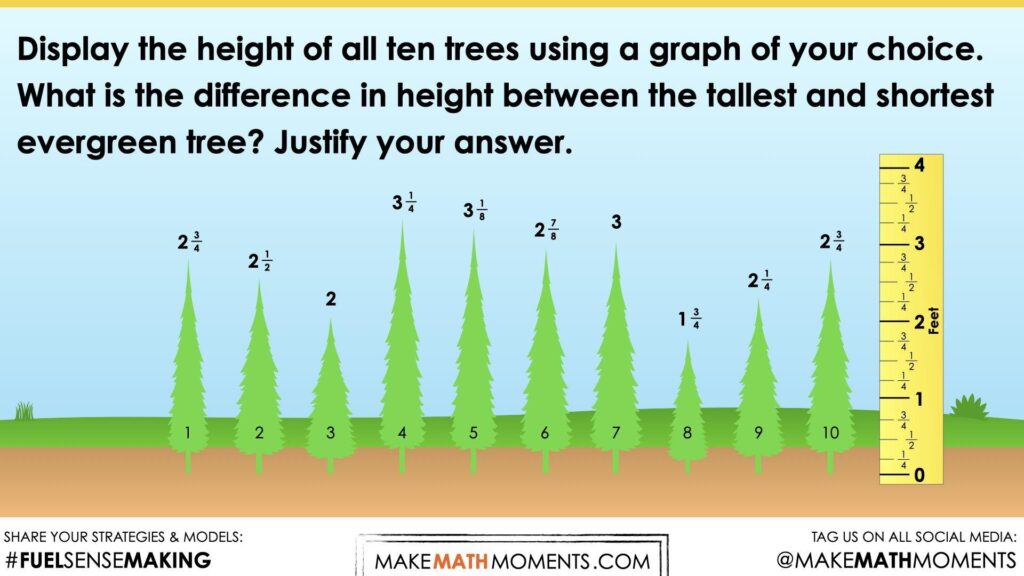
Display the height of all ten trees using a graph of your choice.
What is the difference in height between the tallest and shortest evergreen tree? Justify your answer.
You may choose to offer just the first prompt (graphing) and then the second (finding the difference) if you feel that scaffolding would be helpful for your learners.
During Moves
While Students Are Productively Struggling….
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class.
As you are circulating, consider prompting students to understand why they selected that type of graph and how they determined the scale. Some questions you might consider asking include:
- Why does that type of graph make sense for this data set?
- What other types of graph did you consider?
- What type of data are you working with? How do you know?
- How did you select that scale?
- If your scale had smaller intervals, how would that impact the way your graph looks?
Also, pay attention to how students are determining the difference between the tallest and shortest tree. Are they:
- Using a visual model?
- Using a concrete tool?
- Using an algorithm?
- Using the scale on their graph?
- Counting?
Discuss their thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a representation and justification that does not connect to their understanding.
Student Approaches
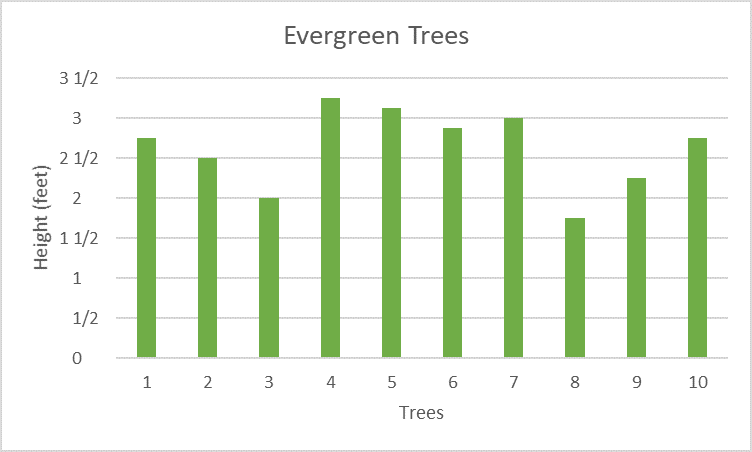
Student Approach #1: Digital Bar Model & Counting
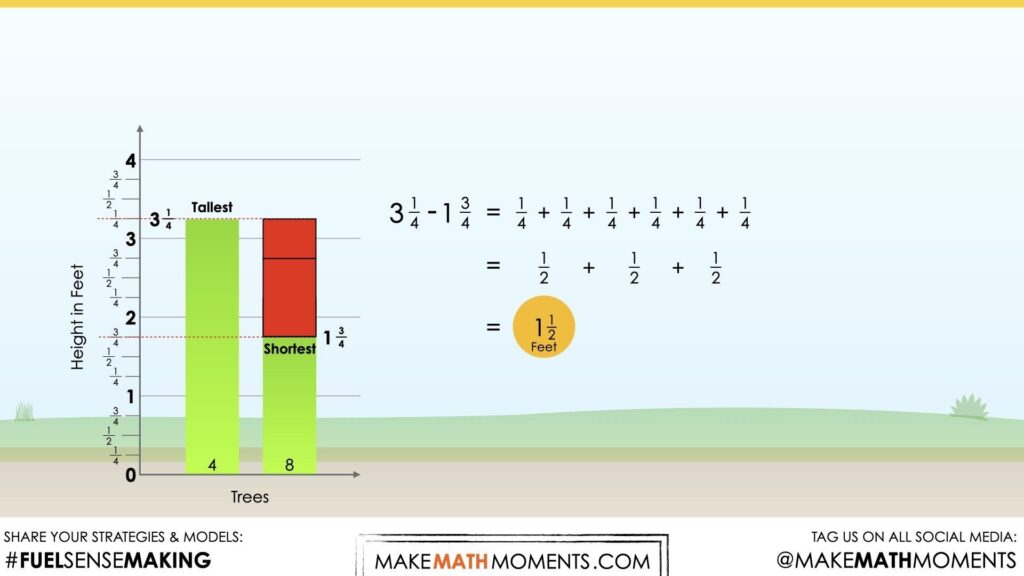
I used excel to create a bar graph. I decided to use a bar graph because each tree’s height is separate from the other trees. The idea is to compare their heights. I noticed that tree 8 is the shortest and tree 4 is the tallest from my graph. Tree 8 is 1\(\frac{3}{4}\) feet and tree 4 is 3\(\frac{1}{4}\) feet. I counted by one fourths from 1\(\frac{3}{4}\) to 2\(\frac{1}{4}\). I counted six one-fourths. Tree 4 is six one-fourths taller.
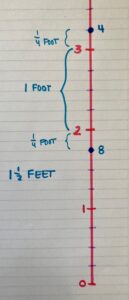
Student Approach #2: Drawn Bar Graph & Linear Model
I decided to make a bar graph to show the heights of all ten trees. I used the lines on my paper. I decided to put eight lines between each foot, because the smallest part was one-eighth. I used the lines to find the different heights and create the bars for each tree. To find the difference between tree four and tree eight, I drew a measuring stick. I marked both heights. I saw the difference between the two trees was one whole foot, and two-fourth feet, which is the same as 1\(\frac{1}{2}\) feet.
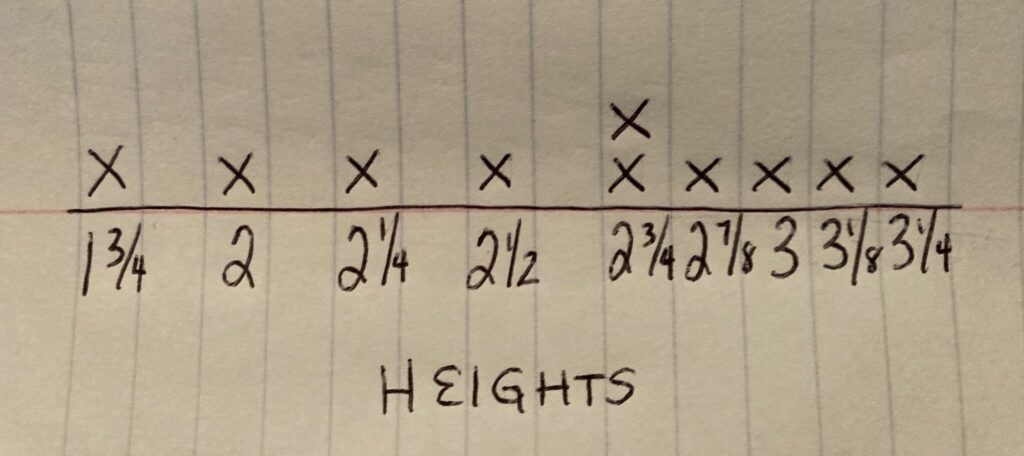
Student Approach #3: Line Plot & Counting On
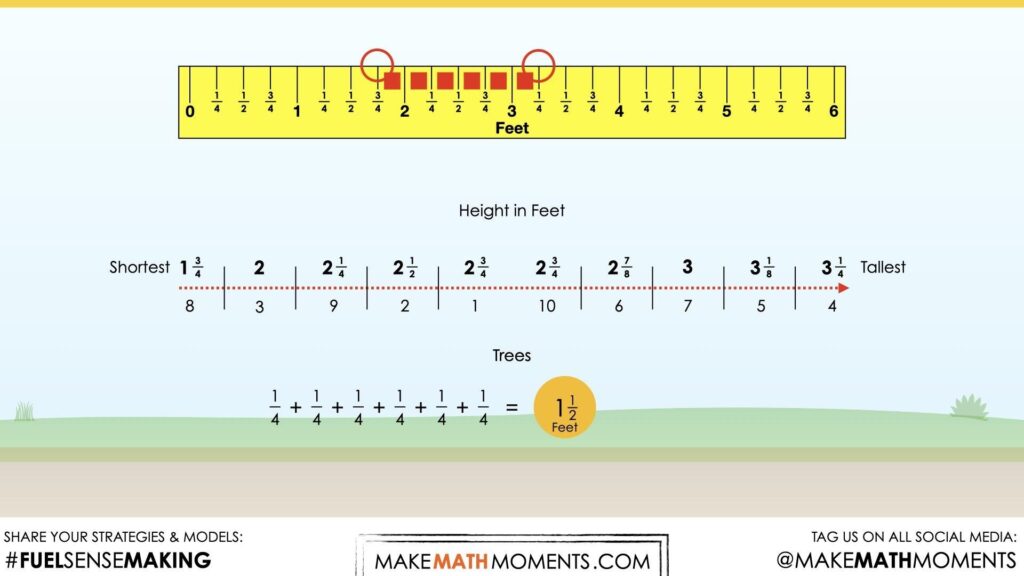
I started by putting the height of the trees in order from least to greatest. I made a number line across the bottom of my page. I decided that every space would be one-eight of a foot. I put an x for every tree. I put two xs on 2\(\frac{3}{4}\) feet because two trees are the same height. I noticed that the smallest tree is 1\(\frac{3}{4}\) feet, and the tallest is 3 and \(\frac{1}{4}\) feet. So I counted up from 1\(\frac{3}{4}\) to 3\(\frac{1}{4}\), and it was 6 fourths, or 1\(\frac{1}{2}\) feet.
Next Moves
Reveal
Depending on how you consolidated the learning by using student solution strategies, you may or may not feel these reveal videos are helpful.
However, if you are just learning to model student thinking and feel it could be helpful for students to see thinking represented visually, consider the following.
In the first reveal video, students see the difference between the tallest and the shortest evergreen trees as a direct comparison of height and we use a counting on strategy with fourths as our unit fraction.
In the second reveal video, students see a more symbolic comparison between the tallest and shortest trees, however the strategy is similar and still accessible.
Consolidation
In today’s consolidation, we will focus on both parts of the student prompt, starting with displaying the data.
Share a few student generated graphs. If any students chose a graph other than a bar graph, you might consider selecting this solution first and discussing the appropriateness of the graph.
In this context, the x-axis (the trees) is categorical data.
Categorical: can be identified based on it’s name or label. Categorical data can be nominal or ordinal (as seen in today’s context).
The purpose for displaying this data is to compare the heights of the different evergreen trees. For these reasons, a bar graph would be an appropriate choice. Bar graphs are used to compare and contrast numbers, frequencies or other measures of distinct categories of data.
Students may have also opted to represent the frequency of each tree height using a line plot.
Consider the scale the students selected. How did they partition the feet? Some students may have partitioned into whole feet, half feet, fourth feet or eighth feet. Consider the advantages of each scale and how the size of the interval impacts the height of the bars.
Explore how students went about determining the difference in height between the tallest and shortest tree. Take the opportunity to explicitly name the operator in this scenario. Students should be aware that they found the difference using subtraction.
3\(\frac{1}{4}\) – 1\(\frac{3}{4}\) = 1\(\frac{1}{2}\)
Some students may describe the difference in half feet, or fourths. This is a great excuse to explore equivalence.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
Why was a bar graph an appropriate choice to display the height of the trees?
Consolidation Prompt #2:
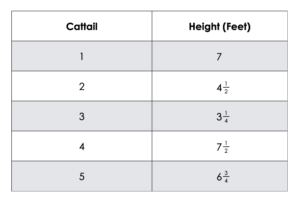
Consider the table below.
a. What scale would you use on the y-axis to display this data? Justify your answer.
b. What is the difference between the shortest and longest cattail?
If this pattern continues, predict how many acorns he will have on day 18. Justify your answer.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!