TAKE A CHANCE

PROBABILITY OF A CHANCE EVENT

Express the probability of a chance event.

Intentionality

Spark Curiosity

Fuel Sensemaking

During Moves

Student Approaches

Consolidation

Reflect and Consolidation Prompts

Resources & Downloads

Educator Discussion Area

Teach This Lesson

Facilitate this lesson with students!
PRESENTATION MODE

Intentionality & Unit Overview

Take a Chance [Day 1] | Data: Probability 3 Act Math Task

Length of Unit: 5 Days

Access each lesson from this unit using the navigation links below

DAY 1
DAY 2
DAY 3
DAY 4
DAY 5

Students will represent the probability of a chance event as a fraction on a probability line. 

Learning goals:

  • We will describe the likeliness of a chance event.
  • We will use fractions to express the probability of a chance event.
  • We will represent the probability on a 0 to 1 number line.

Intentionality…

In this task, students will begin exploring the probability of a chance event. They will represent the likeliness of an outcome as a fraction. Through the consolidation, students will be introduced to the probability line, a 0-1 number line where 0 is impossible and 1 is certain. Some of the big ideas that may emerge in today’s lesson include:

  • Fractions can express the probability of a chance event.
  • The probability of a chance event is a number between 0 and 1, representing the likeliness of the event occurring.
  • Numbers close to 1 indicate greater likelihood, while a probability near 0 indicates an unlikely event.

Spark Curiosity

What Do You Notice? What Do You Wonder?

Show students the following video:

Then, ask students:

What do you notice?
What do you wonder?

Give students 30 seconds (or more) of think time.

Then, ask students to share with their neighbours for another 30 seconds.

Engage in a brief group discussion about the idea of impossible and certain. For example, spinning and landing on the number 20 in this scenario is impossible. However, it is almost certain that you will land on a number between 1 and 12. 

This would be an excellent opportunity to introduce students to the probability line. 

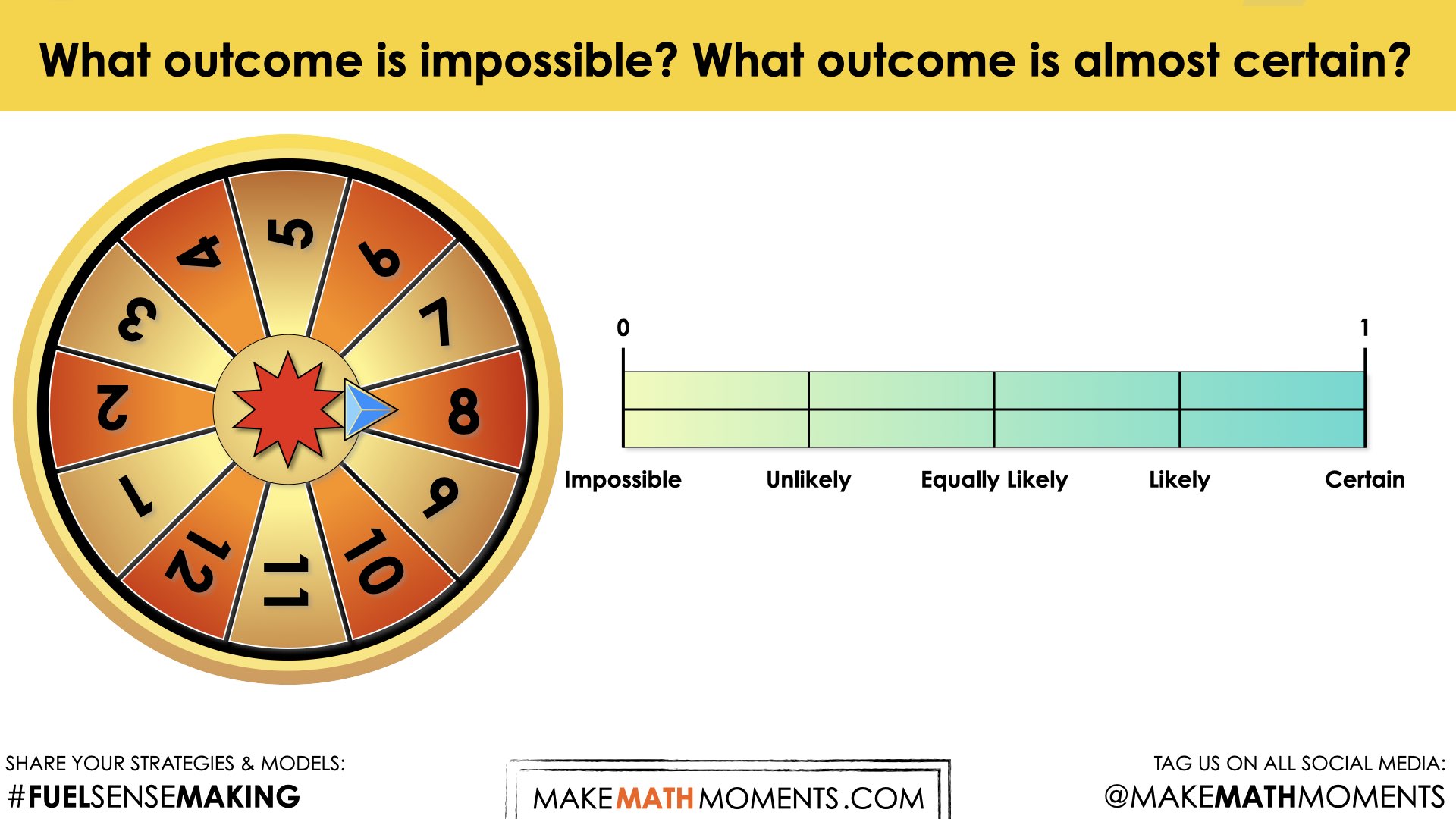
Fuel Sense-making

Crafting A Productive Struggle: Prompt

Since you have already taken some time to set the context for this problem and student curiosity is already sparked, we have them in a perfect spot to help push their thinking further and fuel sense-making.

You can verbally share the following prompt with students:

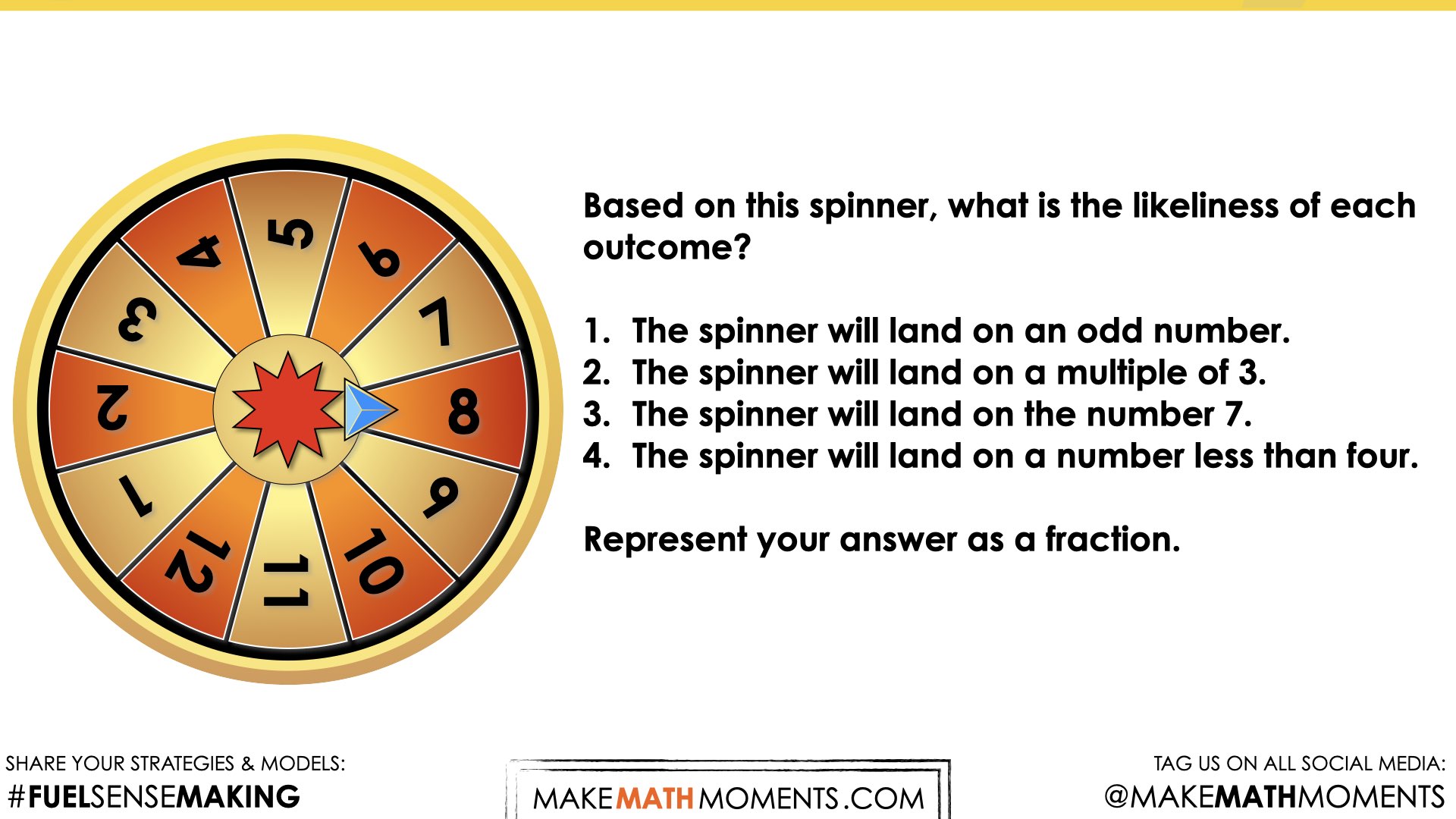
Based on this spinner, what is the likeliness of each outcome? 

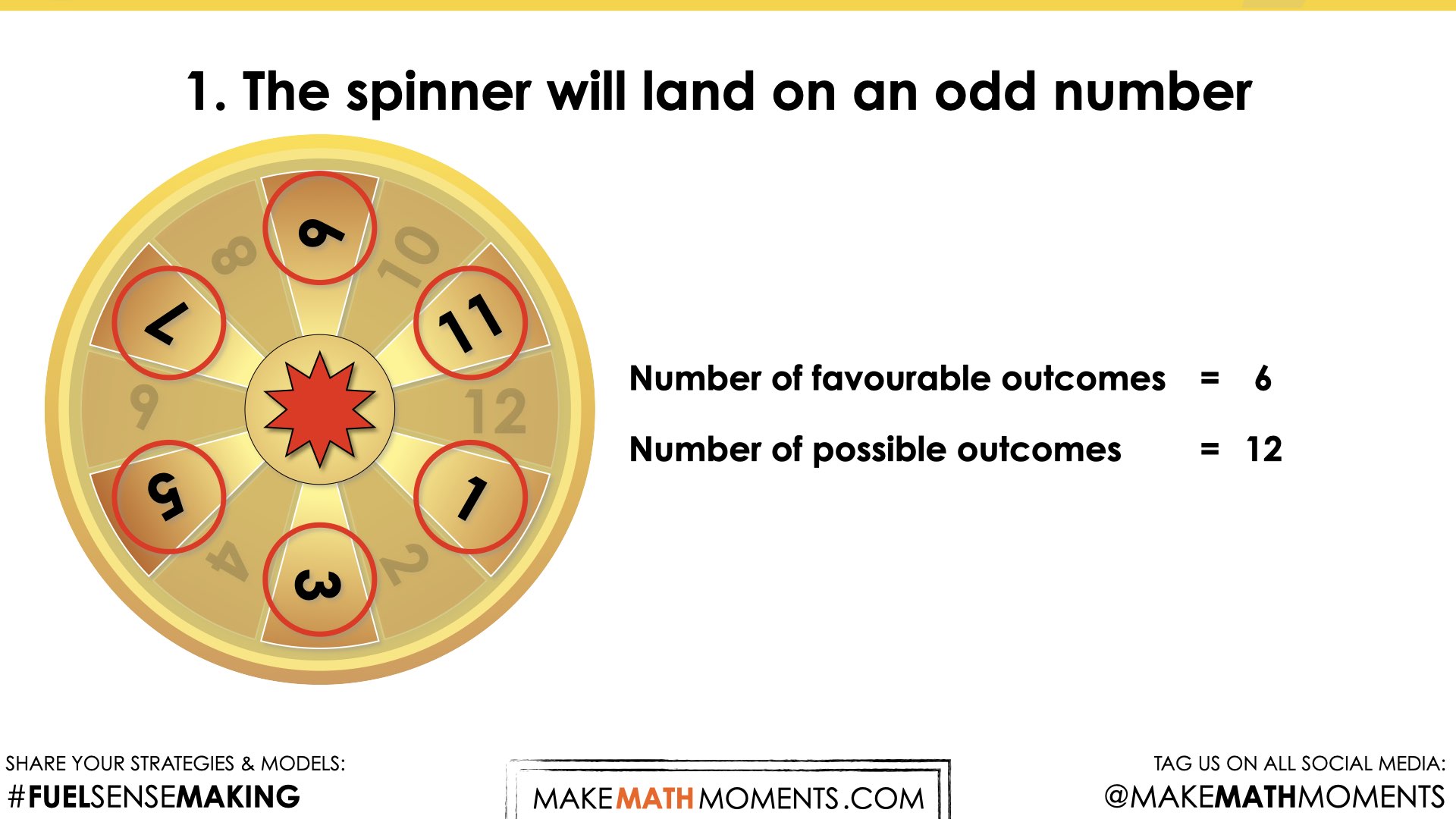
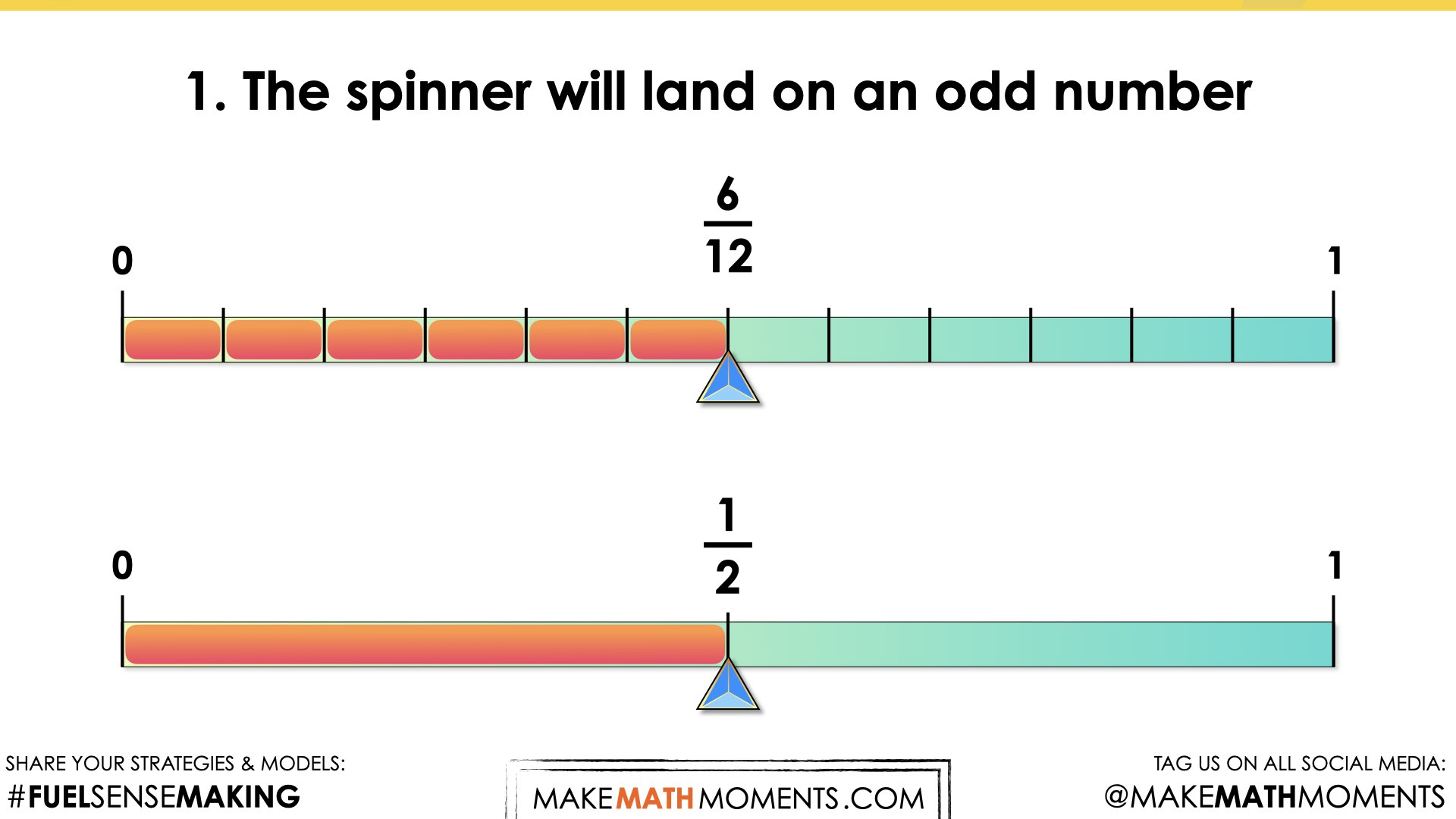
  • The spinner will land on an odd number. 
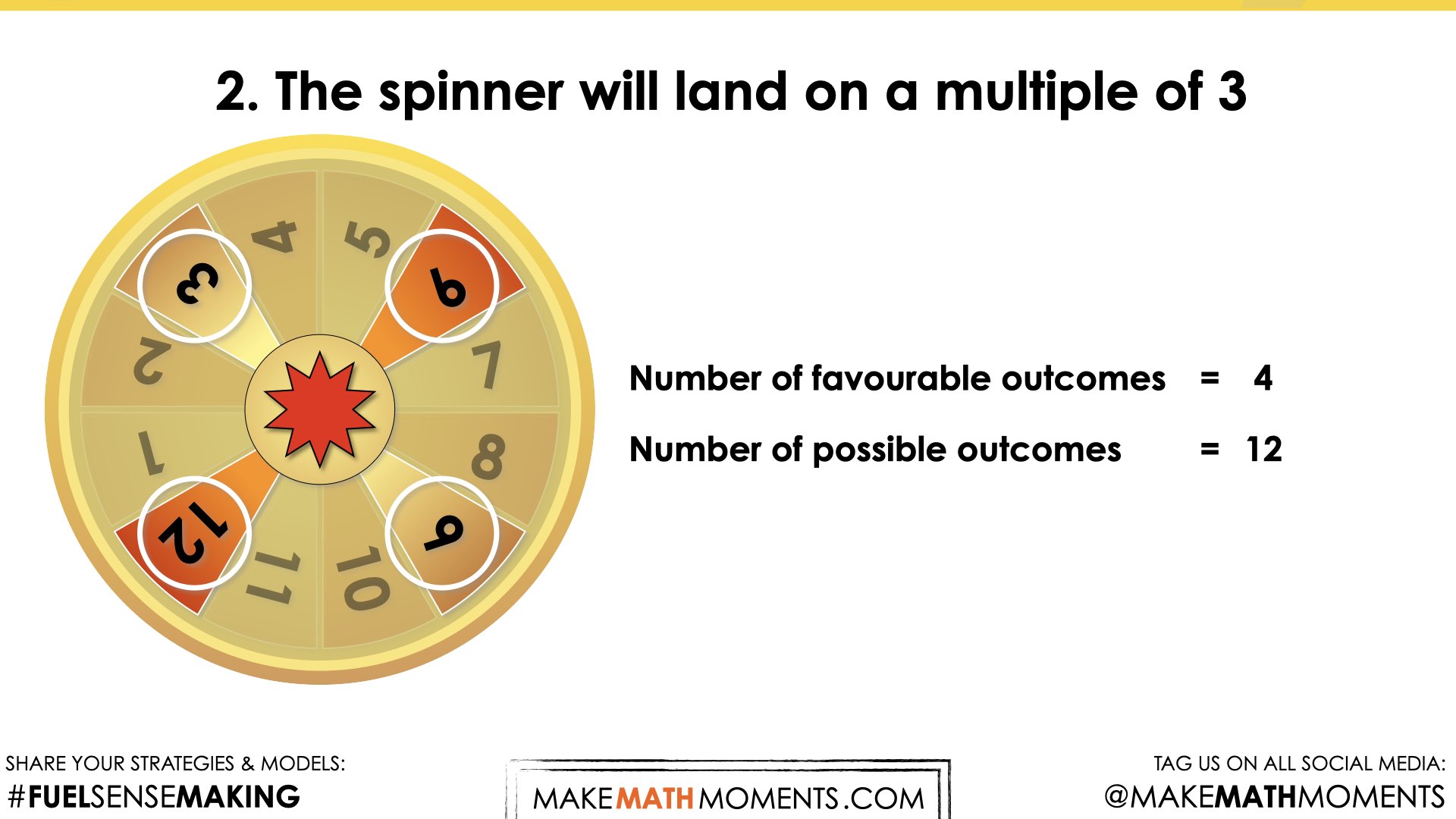
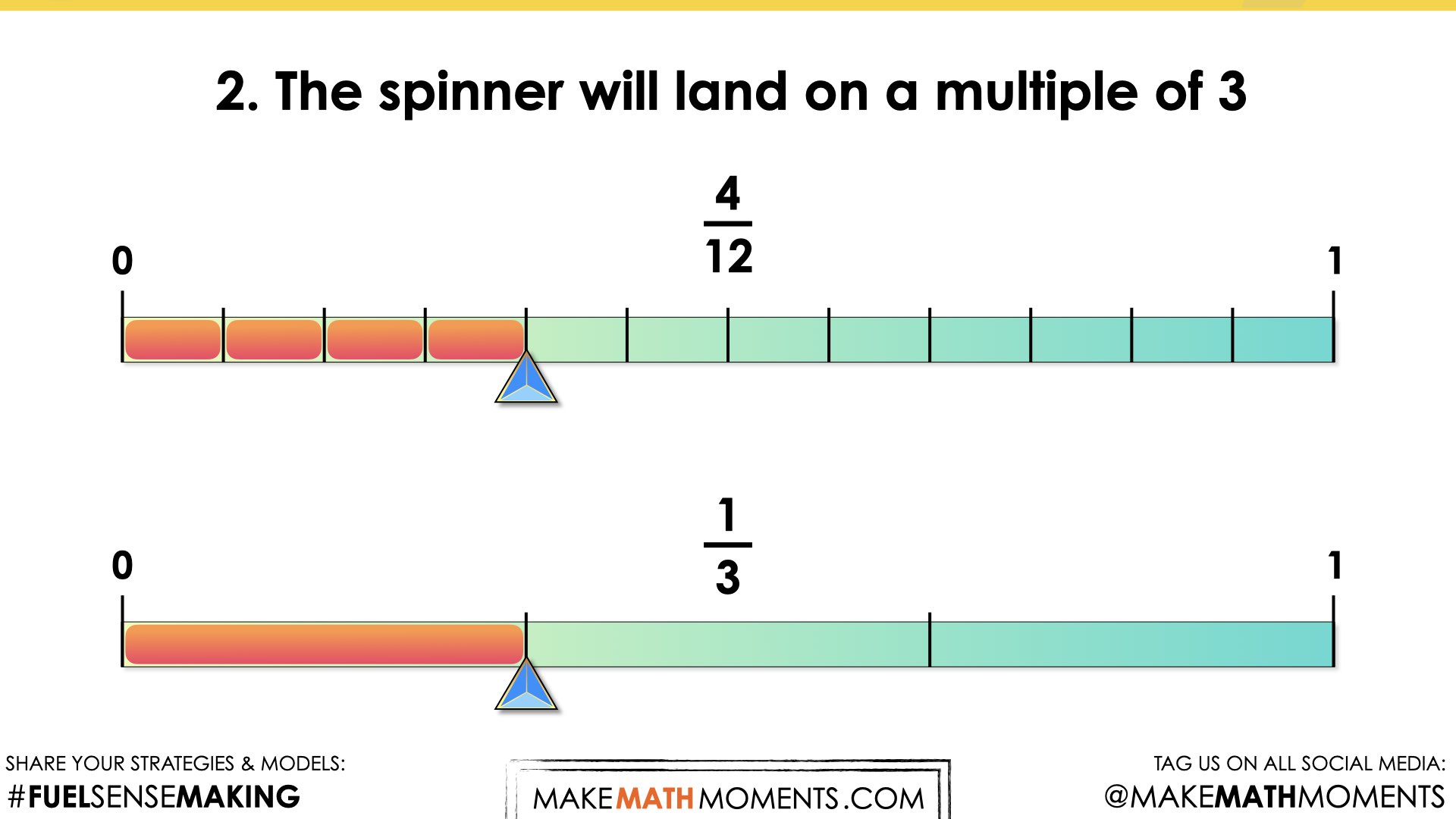
  • The spinner will land on a multiple of 3.
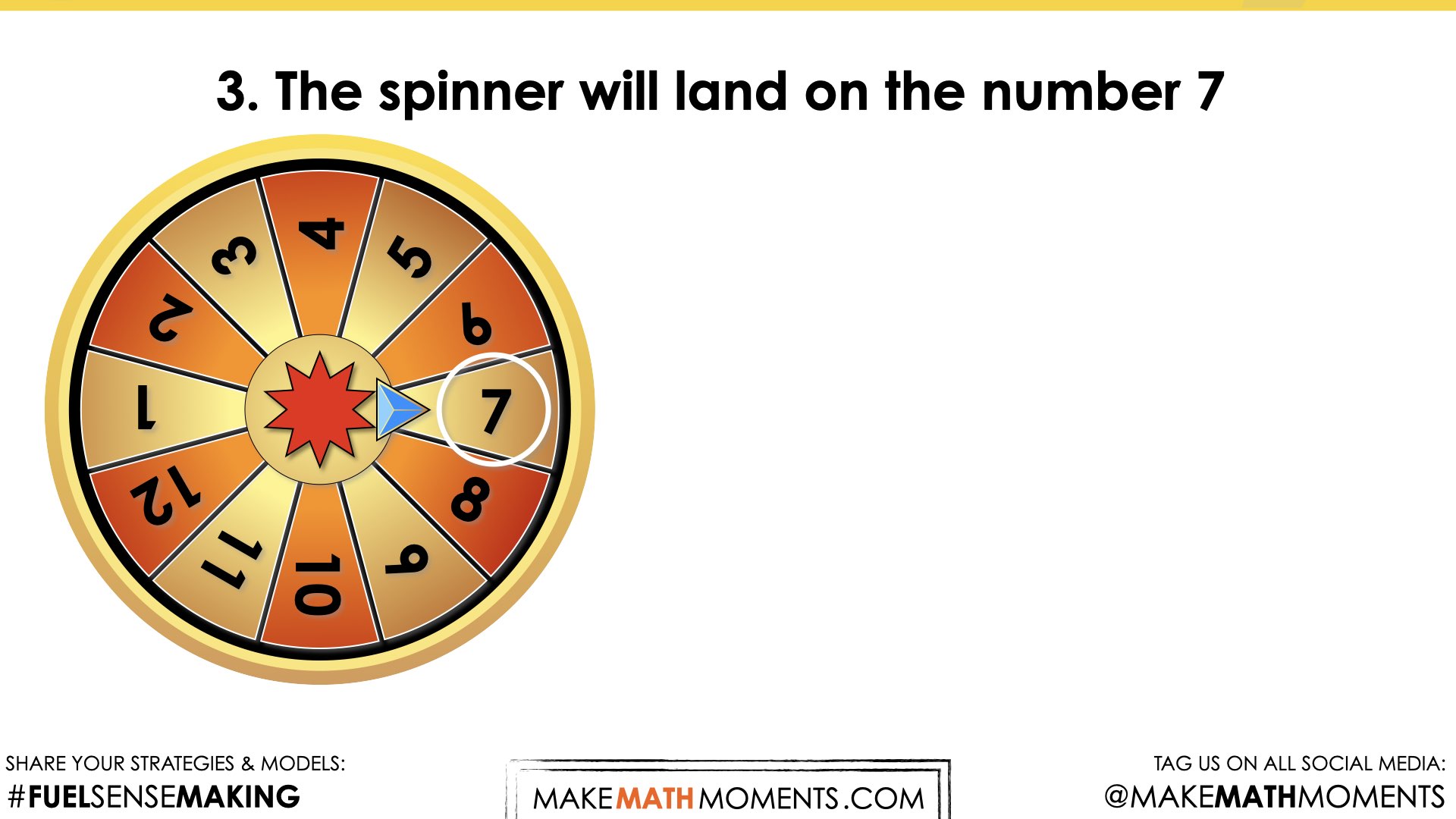
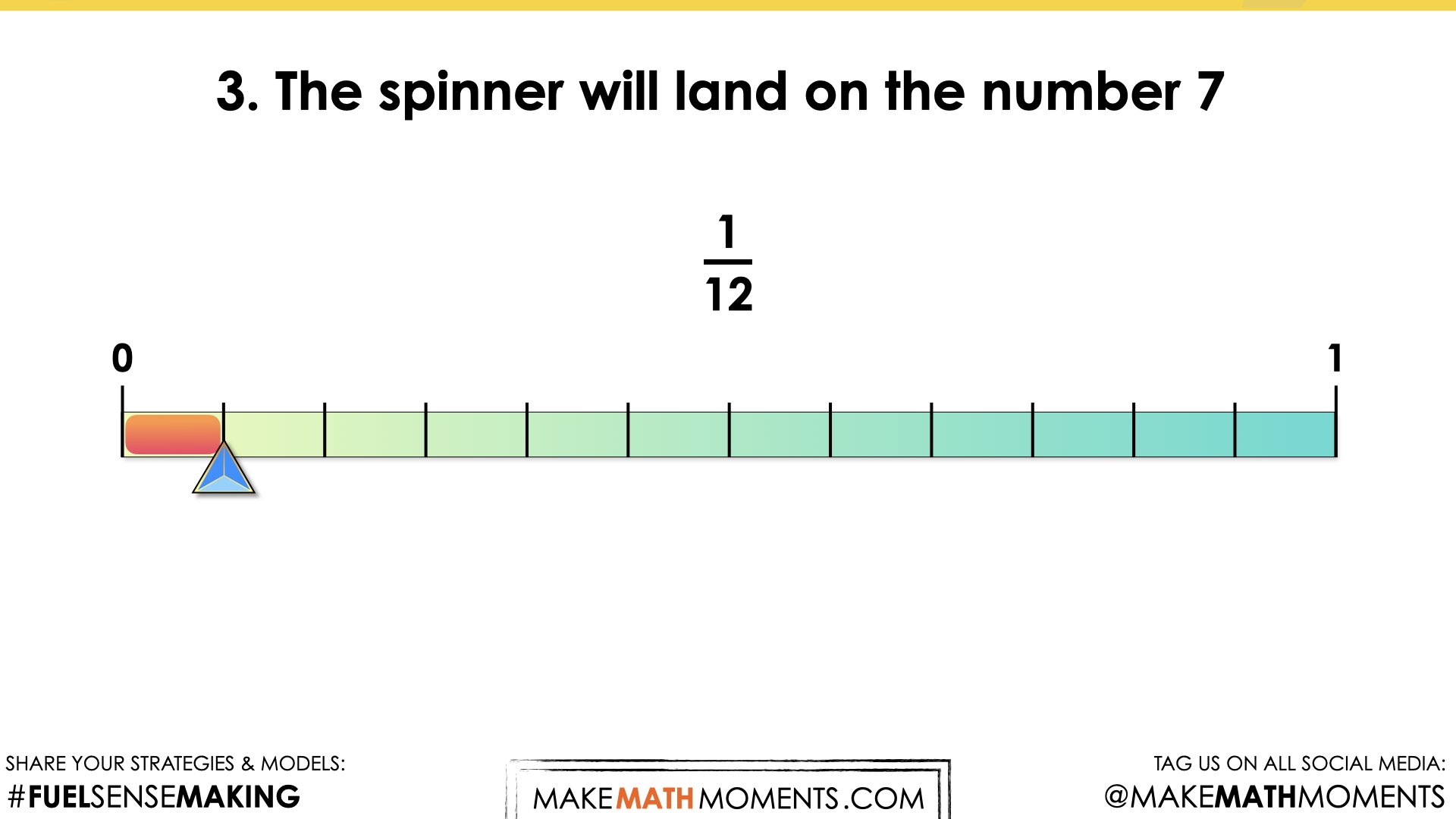
  • The spinner will land on the number 7. 
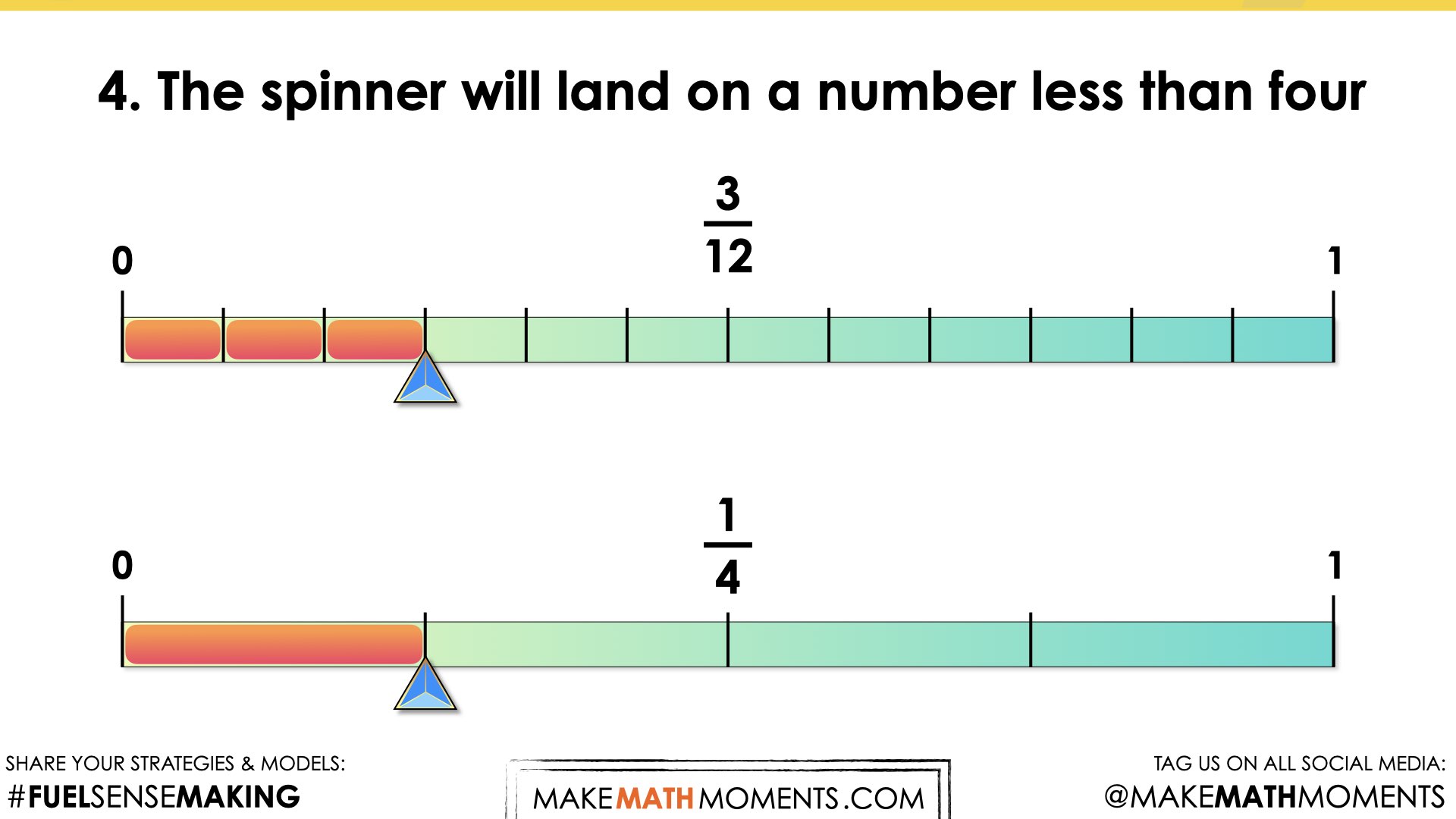
  • The spinner will land on a number less than four. 

Represent your answer as a fraction.

During Moves

While Students Are Productively Struggling…

Monitor student thinking by circulating the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:

  • most accessible to least accessible solution strategies and representations;
  • most common misconceptions;
  • most common/frequent to least common/frequent representations; or,
  • choose another approach to selecting and sequencing student work.

Our goal for this lesson is for students to understand that chance events can be represented as a fraction. We can plot that fraction on a probability line, where 0 is impossible and 1 is certain. 

As you are monitoring, listen for the use of equivalent fractions. For example, are students representing all probability as a fraction expressed in twelfths? Are students discussing halves and fourths? 

When students land on a fraction, refer to the probability line introduced in the spark and consider asking: 

Where would you plot the likeliness of that outcome on our probability line? Is it closer to impossible? Or closer to certain? 

Student Approaches

Student Approach #1: Fractions with a denominator of 12

Since the spinner has twelve parts, I made all the fractions out of twelve. The odd number is 6 out of 12, the multiples of three is 4 out of 12, landing on a 7 is 1 out of 12, and a number less than four is 3 out of 12. 

Student Approach #2: Equivalent fractions

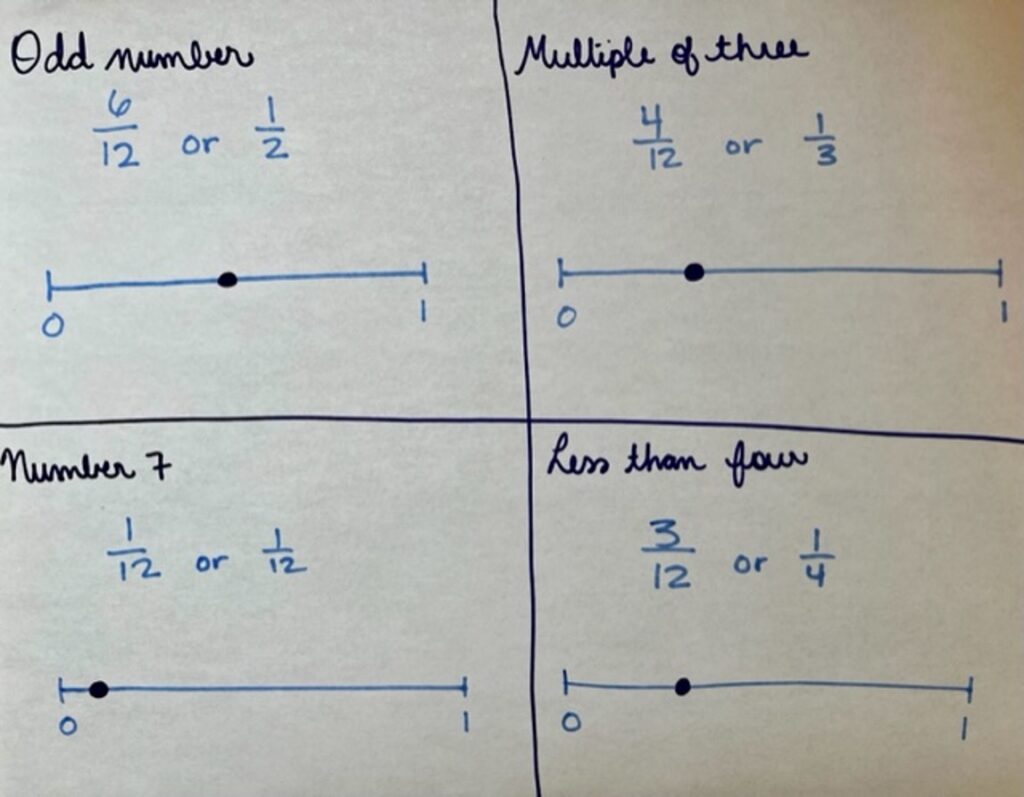
I started by thinking of each scenario as a fraction with twelve parts. But then, it was easier to think of them as a half, a third, and a fourth. Changing the fractions to these equivalent fractions made it easier to represent them on the probability line. 

 

Next Moves

Reveal #1:

Show students the following reveal video:

Reveal #2:

Show students the following reveal video:

Reveal #3:

Show students the following reveal video:

Reveal #4:

Show students the following reveal video:

Consolidation

This consolidation aims to solidify that the probability of a chance event can be expressed as a fraction. The fraction can be represented on a probability number line labelled 0 to 1, with 0 being impossible and 1 being certain. 

Leverage student thinking to explore each of the scenarios. Represent the scenario as a fraction and plot the outcome on the probability line. Support students in making connections between fractions and words to describe the likelihood of events. Words they can use to describe the probability include impossible, certain, equally likely, unlikely, and likely.

Facilitator note: 

This lesson presents an opportunity to explore and confirm equivalent fractions. For example, in the fourth scenario, allow students to discuss and defend that the probability of landing on a number less than four can be expressed as three twelfths or one-fourth. 

Conclude the consolidation by revisiting the learning goals and co-constructing any success criteria that emerged.

For example: 

  • We will describe the likeliness of a chance event.
      • I can use the words impossible, certain, equally likely, unlikely, and likely appropriately to describe the probability of an event or outcome. 
  • We will use fractions to express the probability of a chance event.
      • I can accurately express the probability as a fraction based on the total outcomes.
      • I can express the fraction as an equivalent fraction when appropriate. 
  • We will represent the probability on a 0 to 1 number line. 
    • I can accurately plot and label a probability line based on the likeliness of an event or outcome.

Reflect and Consolidation Prompts

Provide students an opportunity to reflect on their learning by offering these consolidation prompts.

Consolidation Prompt #1:

Describe the probability line below. What can you tell me about this event?

Consolidation Prompt #2:

A bag contains 16 marbles, 8 black, 4 grey and 4 white. If you reach in and pull one marble without looking, what is the probability that you will pick a white marble? Represent the likeliness on a probability line.

We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.

Resources & Downloads

Printable Lesson Plan PDF

Videos, Images & Media Files

Apple Keynote Presentation

Powerpoint Presentation

Printable Consolidation Prompts

Educator Discussion Area

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

Explore Our 60+ Problem Based Units

This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.

Dig into our other units of study and view by concept continuum, grade or topic!

EXPLORE UNITS

Get Tasks, Tips & Tools To Your Email!

__CONFIG_colors_palette__{"active_palette":0,"config":{"colors":{"30800":{"name":"Main Accent","parent":-1},"f2bba":{"name":"Main Light 10","parent":"30800"},"trewq":{"name":"Main Light 30","parent":"30800"},"frty6":{"name":"Main Light 45","parent":"30800"},"flktr":{"name":"Main Light 80","parent":"30800"}},"gradients":[]},"palettes":[{"name":"Default","value":{"colors":{"30800":{"val":"rgb(59, 136, 253)","hsl":{"h":216,"s":0.98,"l":0.61}},"f2bba":{"val":"rgba(59, 136, 253, 0.1)","hsl_parent_dependency":{"h":216,"s":0.98,"l":0.61,"a":0.1}},"trewq":{"val":"rgba(59, 136, 253, 0.3)","hsl_parent_dependency":{"h":216,"s":0.98,"l":0.61,"a":0.3}},"frty6":{"val":"rgba(59, 136, 253, 0.45)","hsl_parent_dependency":{"h":216,"s":0.98,"l":0.61,"a":0.45}},"flktr":{"val":"rgba(59, 136, 253, 0.8)","hsl_parent_dependency":{"h":216,"s":0.98,"l":0.61,"a":0.8}}},"gradients":[]},"original":{"colors":{"30800":{"val":"rgb(59, 136, 253)","hsl":{"h":216,"s":0.98,"l":0.61}},"f2bba":{"val":"rgba(59, 136, 253, 0.1)","hsl_parent_dependency":{"h":216,"s":0.98,"l":0.61,"a":0.1}},"trewq":{"val":"rgba(59, 136, 253, 0.3)","hsl_parent_dependency":{"h":216,"s":0.98,"l":0.61,"a":0.3}},"frty6":{"val":"rgba(59, 136, 253, 0.45)","hsl_parent_dependency":{"h":216,"s":0.98,"l":0.61,"a":0.45}},"flktr":{"val":"rgba(59, 136, 253, 0.8)","hsl_parent_dependency":{"h":216,"s":0.98,"l":0.61,"a":0.8}}},"gradients":[]}}]}__CONFIG_colors_palette__

MAKE MATH MOMENTS ACADEMY

A membership community aimed to accelerate your professional learning journey by supporting mathematics educators as they elevate their pedagogical practice and build their math content knowledge.

Get Started

MEMBER AREAS

CONTACT US

Facebook Twitter Instagram Youtube Spotify
JOIN FREE FOR 30 DAYS