Task Teacher Guide
Be sure to read the teacher guide prior to running the task. When you’re ready to run the task, use the tabs at the top of the page to navigate through the lesson.
In This Purposeful Practice…
Students will identify proportional relationships and apply ratio reasoning to scale in tandem to find unknown quantities. Through this investigation, we will emerge the idea of a scale factor and how it can be used to set up and solve proportions.
Intentionality…
The purpose of the day 2 lesson is to reinforce key concepts from Day 1 to build fluency and flexibility with ratio reasoning through scaling in tandem and to extend this understanding to setting up and solving proportions by revealing scale factors. In particular, the following big ideas may emerge:
- There are two types of ratios; composed unit and multiplicative comparison;
- Thinking of a ratio as a multiplicative comparison involves describing
a quantity as “a number of times greater than another” or describing a quantity as “a fractional part of another” and often (not always) involves a ratio comparing quantities with the same units;
- Ratios can be scaled in tandem to reveal an infinite number of equivalent ratios;
- Although all ratios can be scaled in tandem, ratios thought of as a composed unit lend themselves more naturally to scaling;
- Quotative division is applied when trying to determine a scale factor between two quantities/measures of the same unit (i.e. packs of paper and packs of paper, height and height);
- Scaling ratios in tandem is thought of as a type of ratio reasoning;
- An equation of two equivalent ratios is known as a proportion;
- An unknown quantity from a proportion of equivalent ratios can be found by using quotative division to reveal a scale factor between two corresponding known quantities from both ratios;
- A variety of mathematical models can be used as a tool for solving problems involving a proportional relationship and as a way to represent or prove your thinking. Some of these mathematical models include double bar/double number line models, ratio tables, two variable graphs, and equations;
- The graph of a proportional relationship is linear and crosses through the origin, (0, 0); and,
- The graph is helpful for identifying a trend or relationship between variable quantities and can be helpful when seeking to approximate the value of unknown quantities in that trend and/or relationship.
Math Talk
Overview of This String of Related Problems
The following sequence of problems provides an opportunity for students to apply their ratio reasoning skills to scale in tandem given a proportional relationship involving a composed unit ratio between distance in kilometres and time in minutes.
This context was intentionally selected to promote the use of a linear model like a double bar or double number line model to emerge scaling in tandem. Since this context involves a composed unit ratio – a ratio that can be thought of as a single unit and lends itself to scaling up and down – scaling in tandem is a helpful tool to not only determine unknown quantities, but to also promote student flexibility and fluency with multiplicative thinking.
Throughout this series of visual number talk prompts, be sure to avoid rushing to setting up and solving a proportion as that will defeat the intent of this string of related problems.
If the terms ratio reasoning, composed unit ratios, scaling in tandem and multiplicative thinking are foreign to you, consider deepening your understanding of proportional reasoning by taking our course, The Concept Holding Your Students Back: Unpacking Key Understandings In Proportional Reasoning So You Can Reach Every Student.
Visual Math Talk Prompt #1
Show students the following visual math talk prompt and be prepared to pause the video where indicated:
Then ask students:
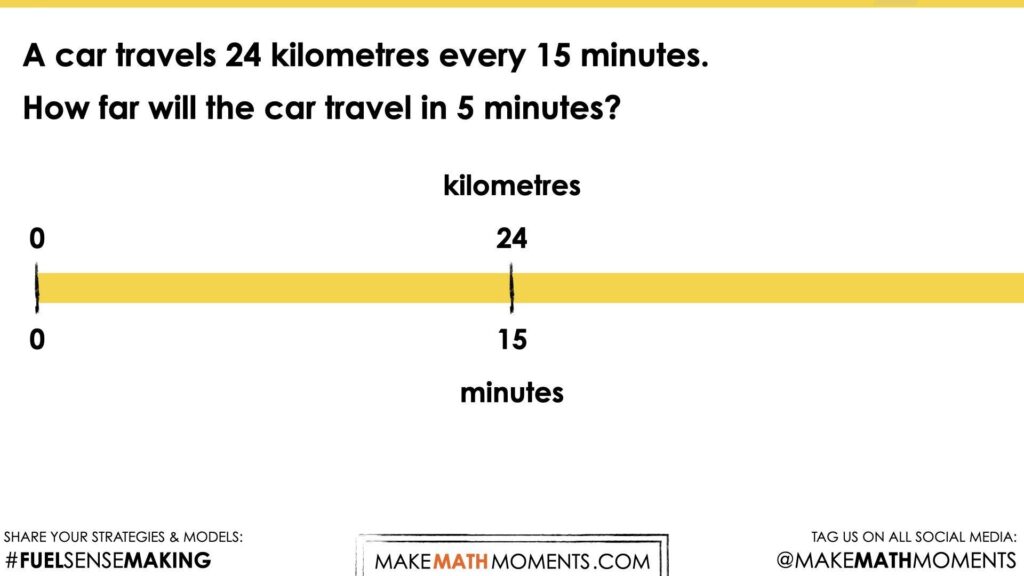
A car travels 24 kilometres every 15 minutes.
How far would the car travel in 5 minutes?
Craft a convincing argument without the use of a calculator.
With this visual up for all to see, give students a reasonable amount of time to reflect on what this question is asking them and to leverage their understanding of magnitude of number to spatially approximate where 5 minutes and the corresponding number of kilometres travelled should be placed on the double number line.
The goal here is to give students a low floor opportunity to leverage their understanding of magnitude as well as to emerge the fractional thinking necessary to determine that 5 minutes is 1 third of 15 minutes.
Since we are working with a composed unit ratio, 24 kilometres to 15 minutes, there are an infinite number of equivalent ratios that exist in this proportional relationship. The ratio x to 5 minutes is only one of those equivalent ratios.
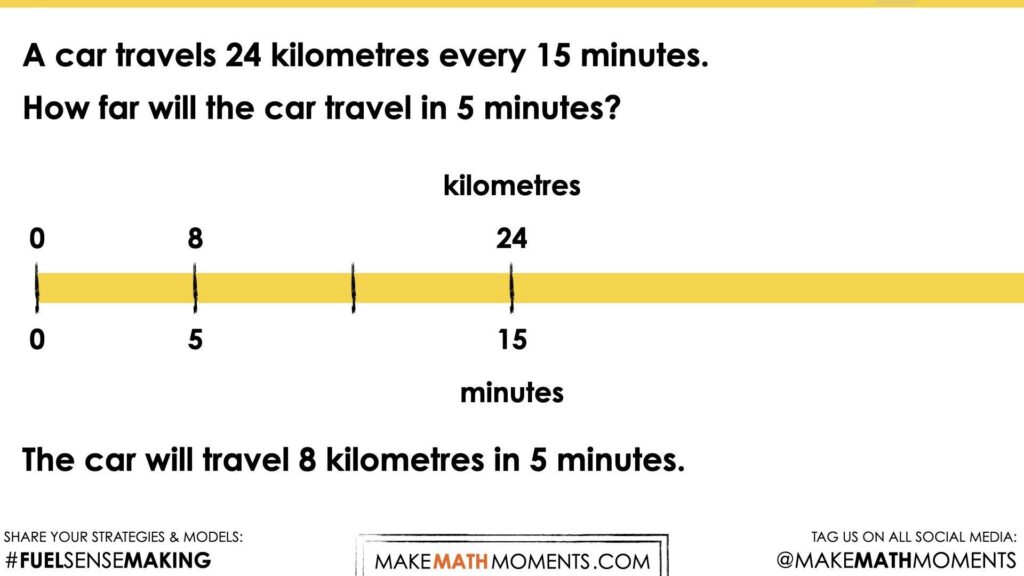
Without much prompting, students should come to the conclusion that since 5 minutes should be placed 1 third of the distance between 0 minutes and 15 minutes, then the number of kilometres travelled 1 third of the distance between 0 kilometres and 24 kilometres should be 8 kilometres.
Note that while some students may be using multiplicative thinking (i.e.: knowing 5 is 1 third of 15), others may be using more of a guess and check approach with additive thinking (i.e.: skip counting by 4s, then 5s to realize that adding 5 repeatedly will get me to 15). Be supportive of any and all strategies students bring to the table, but think of the purposeful questioning you might use to nudge each student forward towards more efficient or “clever” approaches without sounding negative or discouraging.
Something that the facilitator should be able to notice and name here is that the missing quantity that students have solved for here is the same quantity that they would determine when solving this proportion:
\(\frac{24 km}{15 min} = \frac{x km}{5 min}\)
There should be no rush at this point to show students that they have just solved a proportion of equivalent ratios unless students are arriving in your class having already been exposed and/or rushed to an algorithm like cross multiplying, “magic circle” or any other set of steps that they do not understand conceptually. While we will not shut students down from using a trick they have learned previously, we do want to encourage them to work towards crafting a convincing argument as to why their answer is correct. If they cannot convince someone of why their method works, then we can deem their approach a “trick” rather than a justifiable strategy.
Visual Math Talk Prompt #2
Show students the following visual math talk prompt and be prepared to pause the video where indicated:
Then ask students:
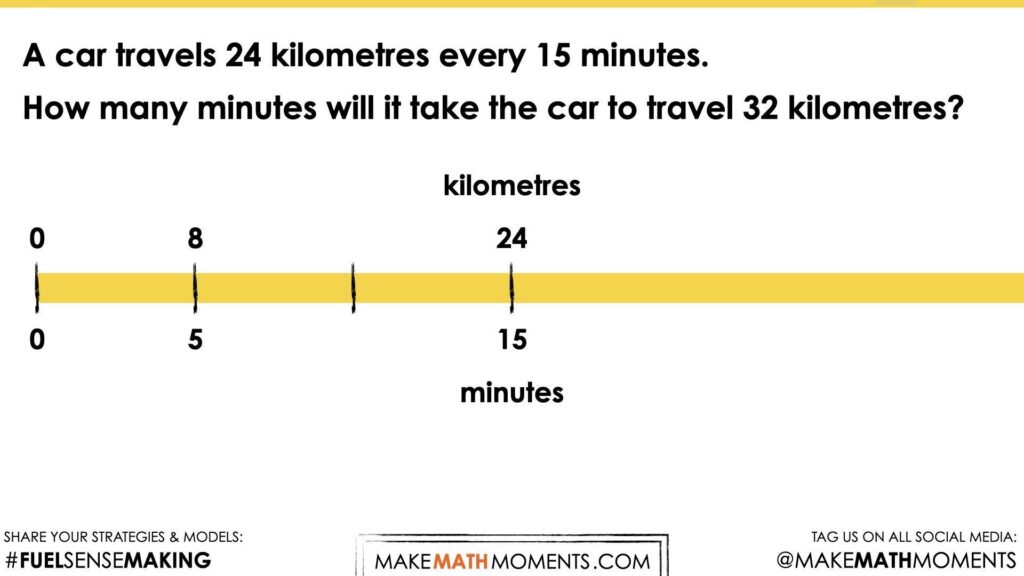
A car travels 24 kilometres every 15 minutes.
How many minutes will it take the car to travel 32 kilometres?
Craft a convincing argument without the use of a calculator.
With this second prompt, you might even consider explicitly asking students to leverage the use of the double number line to support them in solving this problem. While we want to welcome all student generated approaches in our math classroom, we also want to push students outside of their comfort zone. Whether you have a student who is using mental math strategies in their head or a student who has confidence setting up and solving a proportion, we want to nudge these students to bring another mathematical model into their repertoire – not to restrict them from using their tried and true “go to” strategy, but to arm them with more tools to build increased flexibility and fluency.
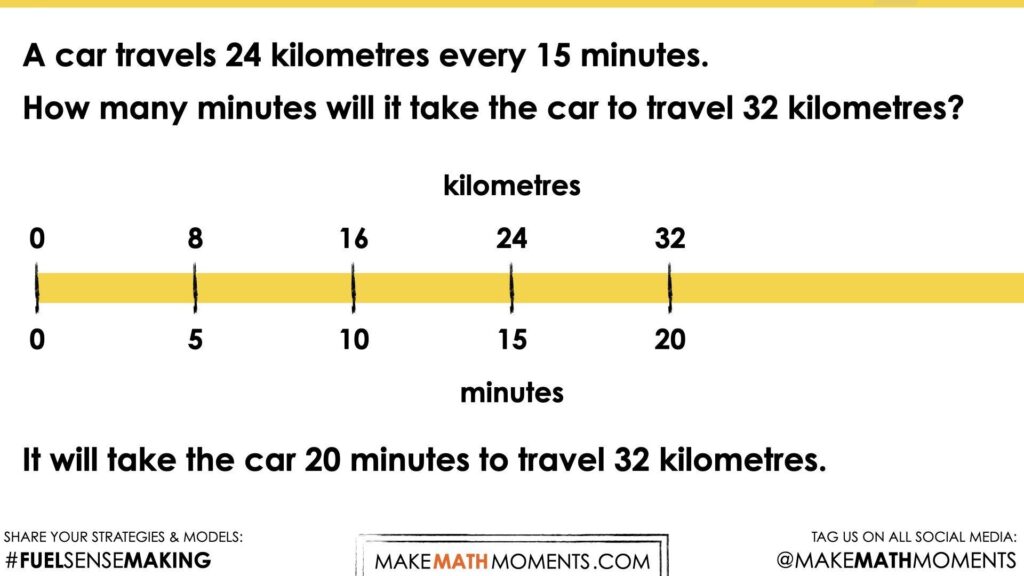
This prompt is yet another situation where the facilitator should be able to notice and name some of the different proportions of equivalent ratios that students might be leveraging in their thinking.
For example, one such proportion is:
\(\frac{24 km}{15 min} = \frac{32 km}{x min}\)
However, some other students might recognize that this is also an equivalent proportion based on our first visual number talk prompt:
\(\frac{8 km}{5 min} = \frac{32 km}{x min}\)
As well as any other number of equivalent ratios can be used to solve this problem. This is an excellent opportunity to highlight to all students why the double number line is a helpful mathematical model to easily scale in tandem multiplicatively to reveal any number of equivalent ratios in the proportional relationship that might help us solve for the unknown quantity we are seeking to find.
Whether students skip count by 8 kilometres and 5 minutes (additive thinking) or extend their thinking from the first visual number talk prompt to double 8 kilometres and 5 minutes to 16 kilometres and 10 minutes before doubling again (multiplicative thinking), the double number line acts as both a tool for all learners to think and represent their thinking as a means to convince others.
Visual Math Talk Prompt #3
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Visual Math Talk Prompt #4
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Spark Curiosity
Estimation: Prompt
Show students this video:
Share the following Estimation Prompt with students:
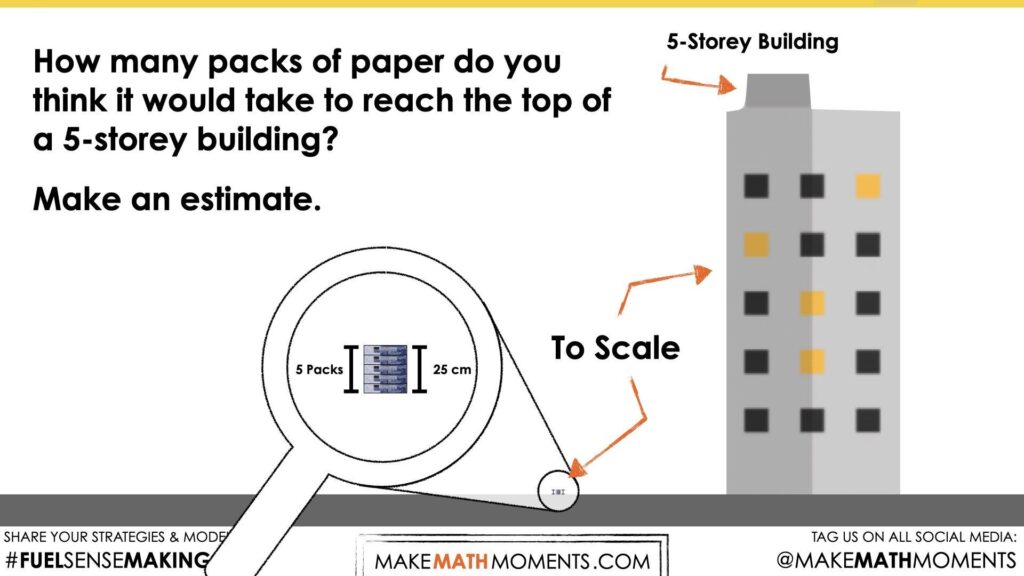
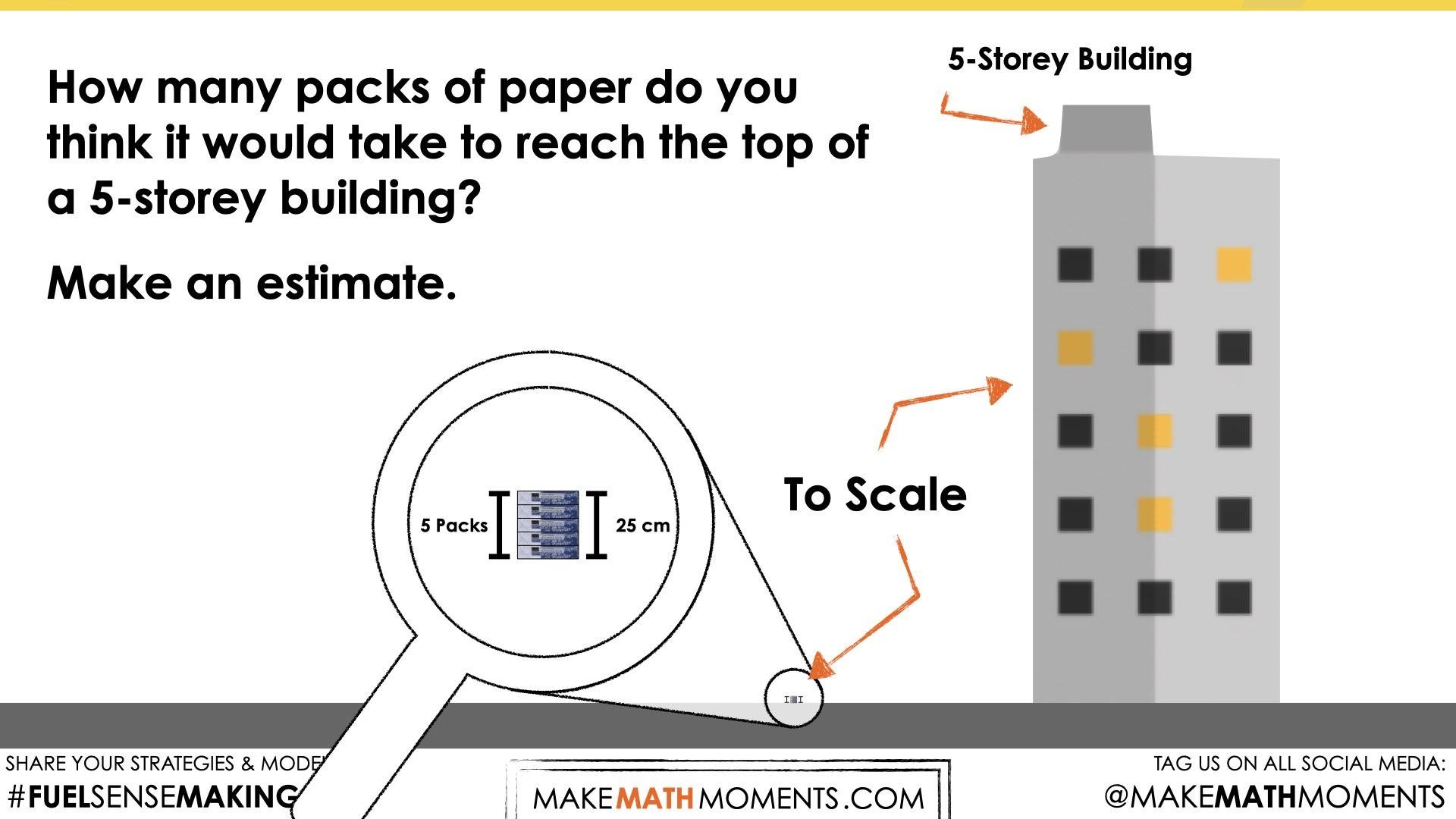
How many packs of paper do you think it would take to reach the top of a 5-storey building?
Make an estimate.
We can now ask students to make an estimate as to how many packages of paper it would take to stack to the height of the 5-storey building. Encourage students to share their predictions and justification with neighbours before welcoming them to the group as a whole.
Note that this is the same stack of 5 packs of paper from Day 1 of this unit and therefore, the height of the stack is 25 cm.
While Students Are Estimating…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Encourage students to use precise mathematical language and listen for the use of additive thinking or multiplicative thinking.
Allow students to share their estimates with neighbours first, then with the class. Write down their estimates on the chalkboard/whiteboard/chart paper so students feel their voices are being heard and so they feel they have a stake in solving this problem. At this point, encourage students to model their thinking so that anyone could be convinced of their estimate.
Are students leveraging what they know about how many packs of paper it took to reach the ceiling from Day 1? Could they use this thinking and simply scale by a factor of 5 since a 5-storey building has 5 floors in total? Should it be more or less than a factor of 5? What other variables might affect estimating in this fashion? Try to encourage students to use what they know to help them come up with a reasonable range for the number of packs required.
Estimation: Reveal
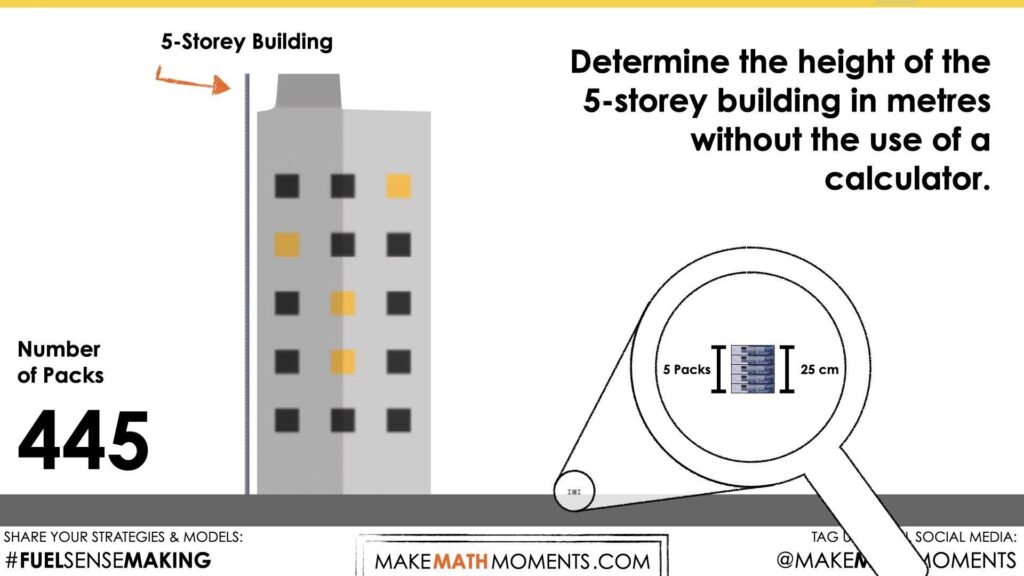
Show the following video to reveal the number of packs it would take to reach the height of this particular 5-storey building:
Did the actual number of packs of paper fall within the range of estimates shared by students in the classroom? If so, be sure to celebrate this and highlight how the more estimates that are shared by a group of people, the more likely it is that the actual amount will fall within that range.
Fuel Sense Making
Crafting A Productive Struggle: Prompt
Now that we know how many packs of paper it would take to reach the height of this particular 5-story building, we will craft a productive struggle for students with this prompt:
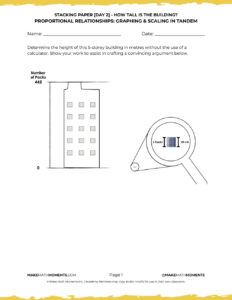
Determine the height of the 5-storey building in metres without the use of a calculator.
Convince your neighbours.
Once again, we are going to promote that students leverage the use of strategies and mathematical models without the use of a calculator to create a convincing argument.
During Moves
While Students Are Productively Struggling…
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
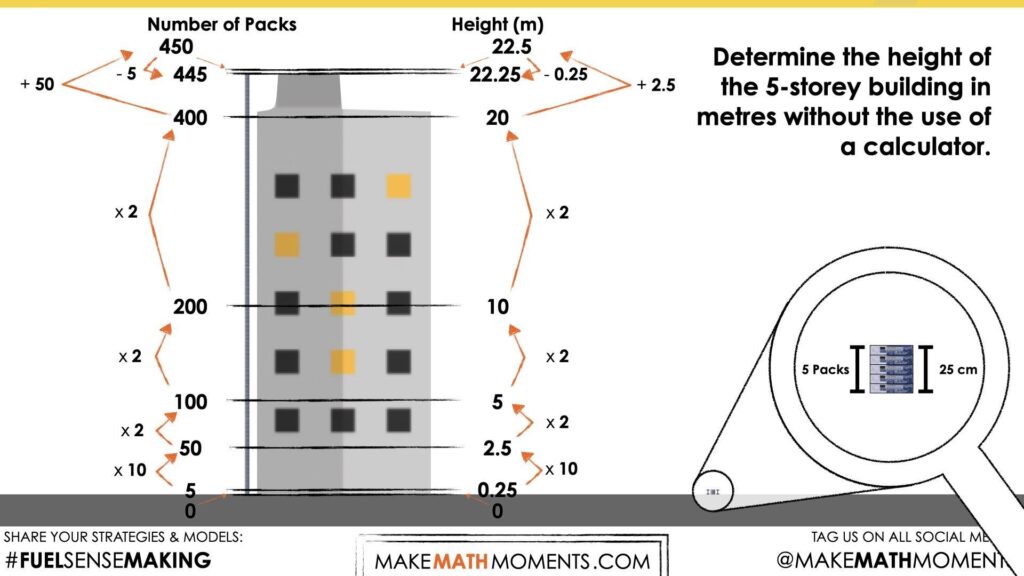
Student Approach #1: Scaling In Tandem Additively With A Double Number Line
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Student Approach #2: Scaling In Tandem Multiplicatively With A Ratio Table
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Student Approach #3: Scaling In Tandem Multiplicatively With Proportions
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Next Moves
Reveal
Show students the following reveal video animation:
Alternatively, you could simply show the final frame of the reveal video below:
Consolidation: Making Connections
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Reflect
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Consolidation Prompt #2:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Consolidation Prompt #3:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Consolidation Prompt #4:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Consolidation Prompt #5:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Download Editable/Printable Handout
Become a member to access purposeful practice to display via your projector/TV, download the PDF to upload to your LMS and/or print for students to have a physical copy
Resources and Downloads
Lesson Tip Sheet

Download the lesson plan in PDF format so you can keep it handy and share with colleagues.
Videos & Images
 Download the videos, images, and related media files to your computer to avoid streaming.
Download the videos, images, and related media files to your computer to avoid streaming.
Keynote Slides
 Download in Apple Keynote format to avoid streaming video and run the lesson smoothly.
Download in Apple Keynote format to avoid streaming video and run the lesson smoothly.
PowerPoint Slides
 Download in Microsoft PowerPoint format to avoid streaming video and run the lesson smoothly.
Download in Microsoft PowerPoint format to avoid streaming video and run the lesson smoothly.
Printable Handout

Download/Edit the handout so you can keep it handy and share with colleagues.
Explore The Entire Unit of Study
This Make Math Moments Task was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, and extensions to elicit and emerge mathematical models and strategies.
Click the links at the top of this task to head to the other related lessons created for this unit of study.
Visual Math Talk Prompt #1
Visual Math Talk Prompt #2
Visual Math Talk Prompt #3
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Visual Math Talk Prompt #4
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Consolidation Prompt #1
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Consolidation Prompt #2
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Consolidation Prompt #3
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Consolidation Prompt #4
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Consolidation Prompt #5
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Download Editable/Printable Handout
Become a member to access purposeful practice to display via your projector/TV, download the PDF to upload to your LMS and/or print for students to have a physical copy