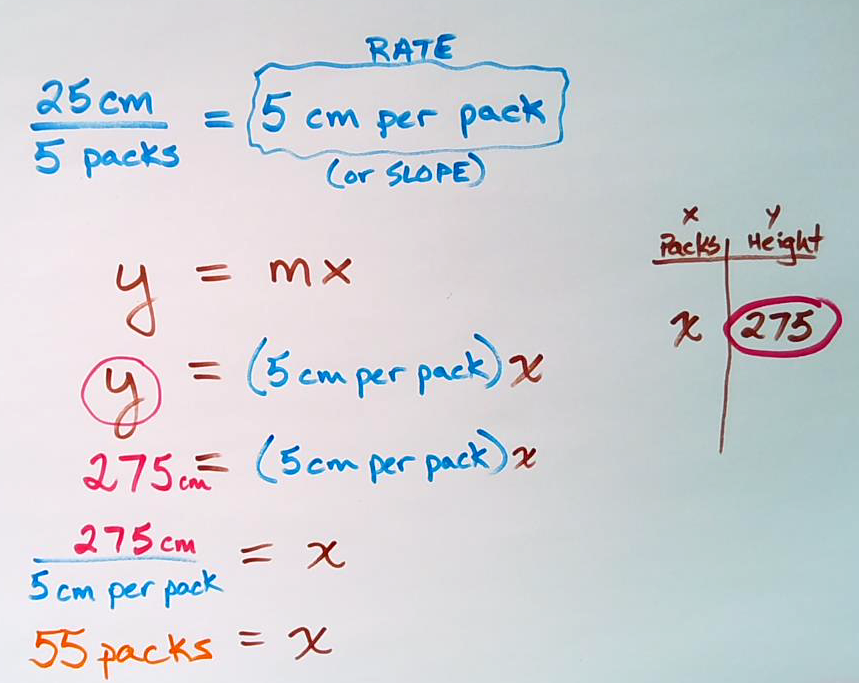STACKING PAPER
PROPORTIONAL RELATIONSHIPS: SOLVING PROPORTIONS
Investigate proportional relationships through ratio reasoning (scaling in tandem) and rate reasoning (constant of proportionality) to solve for unknown quantities.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Current Length of Unit: 1 Day*
*This lesson is the first of an expected 5-day unit. The remaining four (4) days will be released as soon as they are available.
Students will identify the proportional relationship between the height and number of packs of paper stacked vertically on the floor to determine how many packs of paper it will take to reach the ceiling.
In this task, students will determine how many packs of printer paper it will take to reach the ceiling in a photocopy room. Using the height of 5 packages of paper as well as the height of the room, students will leverage their understanding of ratios, rates and proportionality to solve for the unknown quantity: the number of packages of paper.
Some of the big ideas that may emerge in today’s task include:
- There are two types of ratios; composed unit and multiplicative comparison;
- Thinking of a ratio as a multiplicative comparison involves describing
a quantity as “a number of times greater than another” or describing a quantity as “a fractional part of another” and often (not always) involves a ratio comparing quantities with the same units; - Ratios can be scaled in tandem to reveal an infinite number of equivalent ratios;
- Although all ratios can be scaled in tandem, ratios thought of as a composed unit lend themselves more naturally to scaling;
- Quotative division is applied when trying to determine a scale factor between two quantities/measures of the same unit (i.e. packs of paper and packs of paper, height and height);
- Scaling ratios in tandem is thought of as a type of ratio reasoning;
- A variety of mathematical models can be used as a tool for solving problems involving a proportional relationship and as a way to represent or prove your thinking. Some of these mathematical models include double bar/double number line models, ratio tables, two variable graphs, and equations; and,
- An equation of two equivalent ratios is known as a proportion;
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students this video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group.
Some of the noticing and wondering that came up in a class recently included:
- I notice a stack of paper packages on the ground.
- I notice 5 reams of paper.
- There is a clock on the wall.
- The clock says 11:45. Probably the morning, since it is bright outside.
- It looks like the 5 packs of paper is the same width as 1 block in the wall.
- I wonder how many pieces of paper are in each package?
- How many different rectangles are in the image?
- How many packs of paper would it take to reach the ceiling?
- And many more.
At this point, you can answer any notices and wonders that you can cross off the list right away.
Estimation: Prompt
Share the following Estimation Prompt with students:
How many packs of paper does it take to reach the ceiling?
Make an estimate.
We can now ask students to make an estimate as to how many packages of paper it would take to stack to the ceiling. Encourage students to share their predictions and justification with neighbours before welcoming them to the group as a whole.
While Students Are Estimating…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Encourage students to use precise mathematical language and listen for the use of additive thinking or multiplicative thinking.
Allow students to share their estimates with neighbours first, then with the class. Write down their estimates on the chalkboard/whiteboard/chart paper so students feel their voices are being heard and so they feel they have a stake in solving this problem. At this point, encourage students to model their thinking so that anyone could be convinced of their estimate.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Since you have already taken some time to set the context for this problem and student curiosity is already sparked, we have them in a perfect spot to help push their thinking further and fuel sense making.
You can verbally share the following information with students while also sharing the :
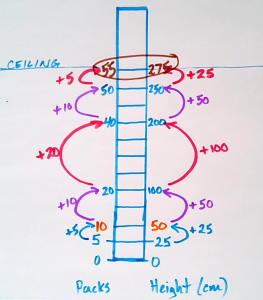
If 5 packages of paper have a height of 25 cm, how many packs of paper will it take to reach the ceiling height of 275 cm?
Convince your neighbour.
Once again, we are going to promote that students leverage the use of strategies and mathematical models without the use of a calculator to create a convincing argument.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common misconceptions;
- most common/frequent to least common/frequent representations; or,
- choose another approach to selecting and sequencing student work.
The graphical representations you might see students include:
- Double bar model;
- Double number line;
- Ratio table;
- Proportional reasoning leveraging various operations symbolically;
- Graphical representation;
- Setting up and solving a proportion; or,
- Creating and solving an equation.
Regardless of which strategy and/or approach students take to solve this problem, ensure that you push their thinking further by asking them to convince you and/or their neighbours.
This might be challenging for some students – especially those who are able to quickly leverage their operational sense and/or a procedural approach like setting up and solving a proportion.
For example, if a student constructs a proportion of equivalent ratios in fraction form, such as:
25 cm/5 packages = 275 cm / x packages
This would suggest that this student has explored setting up ratios and rates in the past and may leverage a procedure such as cross multiplication or some other series of steps to solve proportions.
While we will not discourage students who have learned cross multiplication or some other form of solving proportions procedurally, we do want to push students to explain why their procedure works. Students will not enjoy this – at least initially – however, this is the only way that we can push students to truly fuel their sense making.
Encourage students who are solving the problem procedurally, but do not have a convincing argument for why their solution works, offer them some suggestions for models like a double bar model (i.e.: essentially ‘drawing’ a diagram of what the giant stack of paper packages would look like.
Discuss their thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a representation and justification that does not connect to their understanding.
Student Approaches
Student Approach #1: Double Bar Model and Additive Thinking
I created a visual of the packs of paper being stacked up to the ceiling and worked my way through addition. I started by adding 5 packs and 25 cm, then started to add more and more until I reached a height of 275 cm which was a total of 55 packs.
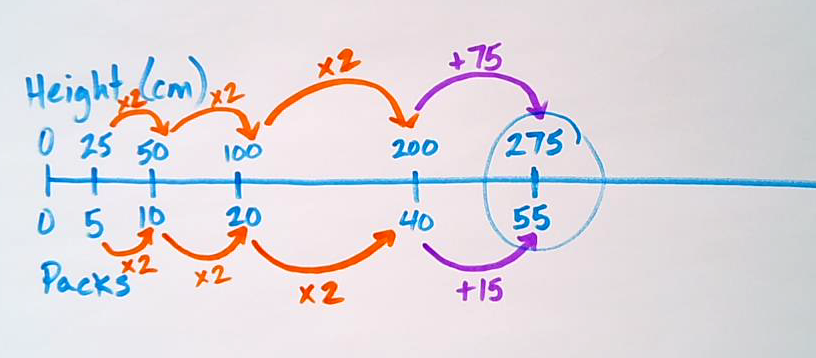
Student Approach #2: Double Number Line and Multiplicative Thinking
I used a double number line to scale from 5 packs of paper and 25 cm by doubling multiple times to get me close to the ceiling height. Once I had 40 packages and 200 cm of height, I needed 75 more cm which was 15 more packages for a total of 55 packages.
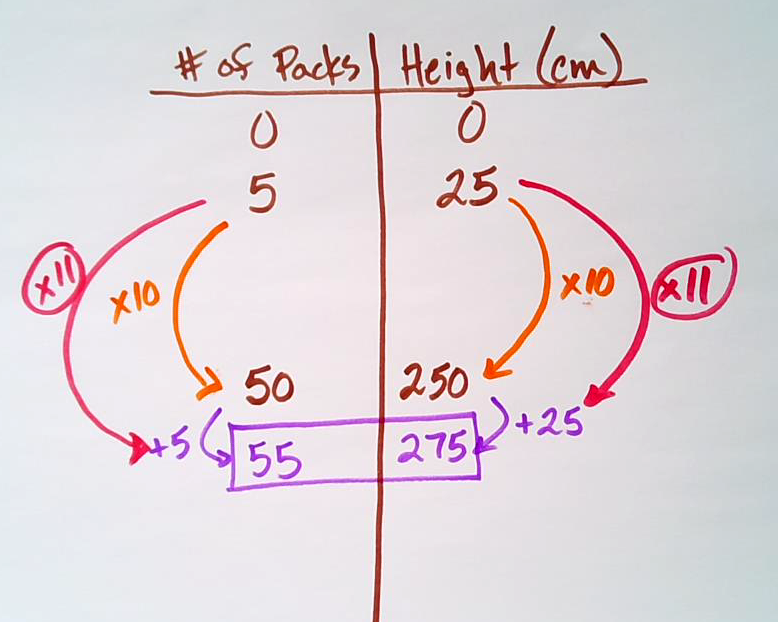
Student Approach #3: Ratio Table Using Multiplicative Thinking & Ratio Reasoning
I used a ratio table to show equivalent ratios comparing number of packages and total height in centimetres.
Since I know I can multiply 5 packs of paper by 10 and 25 cm by 10 to get 250 cm, I’m only 25 cm away from the ceiling. By adding another 5 packages, I’ll be at the total height of 275 cm.
Therefore, it would be 55 packages in total.
Student Approach #4: Ratio Table Using Multiplicative Thinking & Rate Reasoning
Since 5 packs of paper have a height of 25 cm, I can quickly divide 25 cm by 5 packages to find my rate (or slope) of 5 cm per pack.
From here, I can simply divide 275 cm by 5 cm per pack or find 1 fifth of 275 cm to get 55 packages in total.
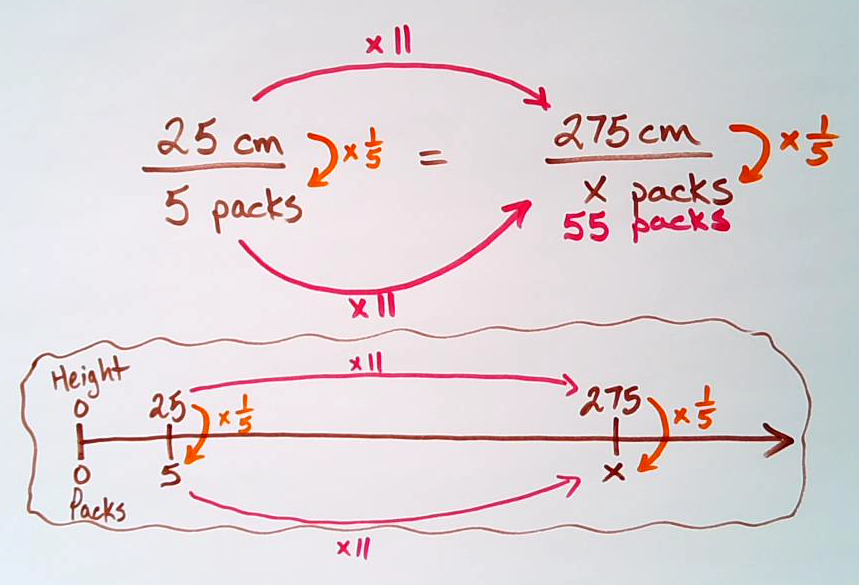
Student Approach #5: Setting Up and Solving a Proportion
Since this problem involves a ratio of 5 packages to 25 cm of height, I can set up and solve a proportion.
In order to figure out how many times bigger 275 cm is than 25 cm, I can divide 275 cm by 25 cm, which is 11. That means there are 11 groups of 25 cm in 275 cm. This also means that there must be 11 groups of 5 packages or a total of 55 packages.
Facilitator Note:
The image shares a quick connection to how a proportion can be thought of as zooming in on two ratios along the double number line and thus the same ratio reasoning (scaling) or rate reasoning (using the rate) can be leveraged to solve any proportion. These strategies encourage the fuelling of sense making in students and should be promoted over the memorization of a procedure such as cross multiplication.
Student Approach #6: Setting Up and Solving an Equation
Since I know that this relationship is proportional and therefore a direct variation linear relationship, I can create the equation of a line in slope/y-intercept form, y = mx + b.
Since it is proportional, the initial value, b, is equal to 0.
I can find the rate of change (or slope, m) by dividing 25 cm by 5 packs of paper revealing a rate of 5 cm per pack.
Therefore, substituting in 5 for m and 275 for y and solving the equation reveals an x value of 55 or 55 packs of paper.
Next Moves
Consolidation
While students may or may not share approaches that involve ratio tables, proportions, or using an algebraic equation, the focus of the consolidation today will be to ensure all students are able to visually and/or symbolically scale the 5 pack to 25 cm ratio in tandem.
Leveraging the following silent solution visual animation highlights scaling in tandem utilizing a double-bar model which can easily be thought of or consolidated to a double number line.
The intent is to ensure that students can begin to see that the ratio relationship between the number of packages and the height of the stack can be multiplicatively scaled in tandem.
Student prompt:
What happens to the height if we double the number of packs of paper?
…triple?
What happens to the number of packs of paper if we fifth the height of the stack?
Notice that the prompts above involve multiplicative thinking where we are multiplying one quantity by a scale factor and doing the same for the other quantity.
It could be worth asking students to think additively as well by stating:
What happens to the height if we add 5 packages of paper?
While students are welcome to solve problems involving quantities whose relationship is proportional using any strategy, our goal is to nudge all students from additive thinking towards multiplicative thinking, if possible.
Of course, if your students have experience working with proportional relationships with double number lines, ratio tables, graphs and algebraic equations, you are welcome to consolidate these ideas here as well. However, it should be noted that we will intentionally bring these representations out in the next lesson.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering this consolidation prompt to be completed independently.
Consolidation Prompt #1:
How many packs must you stack to reach a total stack height of 150 cm?
Consolidation Prompt #2:
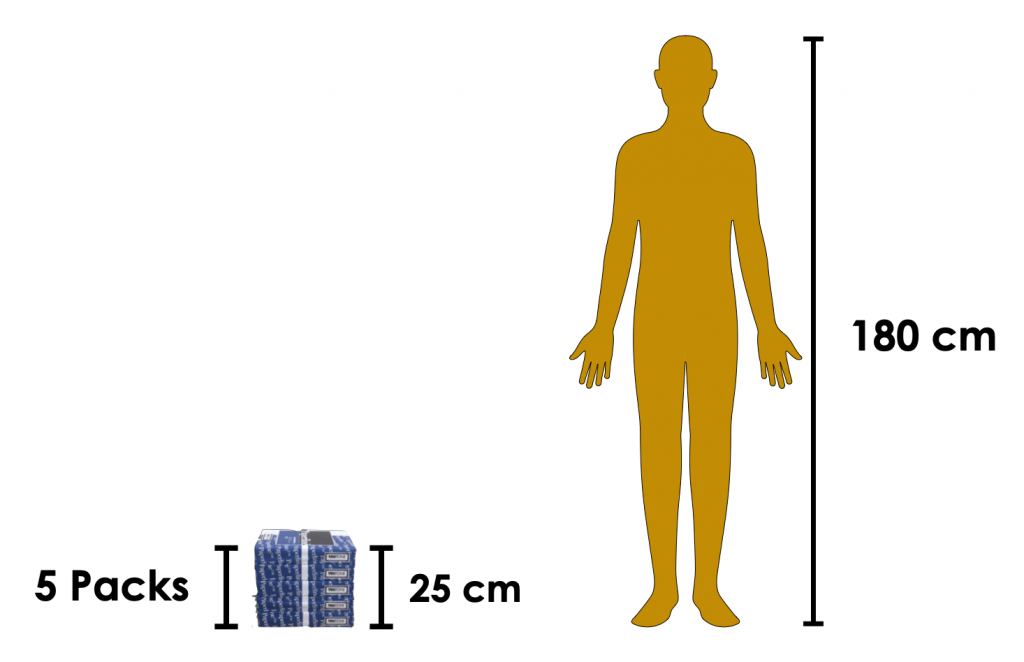
How many paper packs would it take to reach the height of Abdullah who is 180 cm tall?
Use a mathematical model to represent your thinking.
Consolidation Prompt #3:
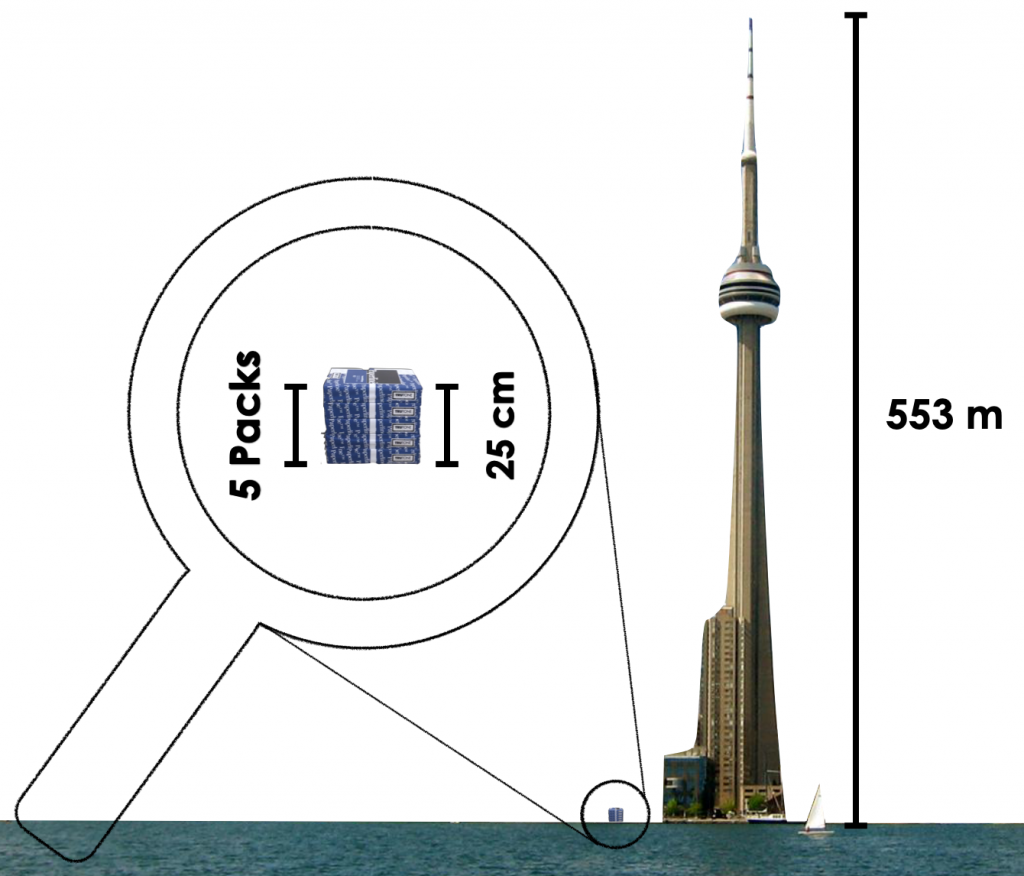
The CN Tower in Toronto, Canada is 553 m tall.
How many paper packs would it take to reach the height of the CN Tower?
Use a mathematical model to convince your neighbour.
Consolidation Prompt #4:
The Renaissance Center in Detroit, Michigan has a height of 221 m. How many packs of paper would you need to reach the top?
Use a mathematical model to construct your argument.
Consolidation Prompt #5:
A stack of 8 packs of paper of a different brand has a height of 72 cm.
- How tall would a stack of 24 packages be?
- How many packs would it take to reach a height of 36 cm?
Use a mathematical model of your choice to convince the reader.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!