Task Teacher Guide
Be sure to read the teacher guide prior to running the task. When you’re ready to run the task, use the tabs at the top of the page to navigate through the lesson.
In This Purposeful Practice…
Students will represent fractions and decimal hundredths. Students will explore the relationship between decimals and fractions. They will add decimals and fractions.
Intentionality…
The purpose of the Day 2 activities is to reinforce key concepts from Day 1. Students will engage in a string of related problems through a math talk and will have an opportunity to complete independent purposeful practice.
Today’s activities should be completed without the use of a calculator. The math talk and purposeful practice serve to develop a deeper understanding of the following big ideas.
Number:
- Fractions can be represented in a variety of ways;
- Fractions (and their decimal representation) represent values relative to a whole (for example, one whole dollar).
- Quantities represented as a decimal are fractions limited to base ten denominators (i.e.: tenths, hundredths, thousandths, etc.)
- Standard representation of coin values are expressed as decimal hundredths.
- Quantities can be represented using a variety of symbolic notations and maintain equivalence.
Visual Math Talk
Related String of Problems
$0.25 + $0.10 + $0.50 + $0.30 + $0.05
\(\frac{1}{4} + \frac{1}{10} + \frac{2}{4} + \frac{3}{10} + \frac{1}{20}\)
0.25 + 0.1 + 0.5 + 0.3 + 0.05
\(\frac{2}{10} + \frac{3}{4} + \frac{3}{20} + \frac{1}{4}\)
Encourage students to model the numbers of each addition sentence and solve. Some students may benefit from working with the actual coins in order to model and solve. Consider finding an opportunity to model using a linear bar model.
You will notice that the first three expressions are equivalent. The purpose here is to reinforce equivalence. The goal is for students to see that regarding some decimals and fractions as money (or coin values) can be helpful when operating. The fourth expression in this string will encourage students to apply this strategy.
Facilitator Note:
Watch for students who are students moving addends around using the commutative property.
For example, do they tend to add the quarter first, and then the dime?
In the fourth addition sentence, pay attention to how students handle the \(\frac{3}{4}\) and \(\frac{1}{4}\).
Do they collect the four quarters?
This approach may serve as an opportunity to explore “collecting” like values before solving which is a precursor to collecting like terms algebraically.
Visual Math Talk Prompt #1
If you plan on using the visual number talk prompt videos to make this process as visual as possible, begin playing the video and be prepared to pause where indicated.
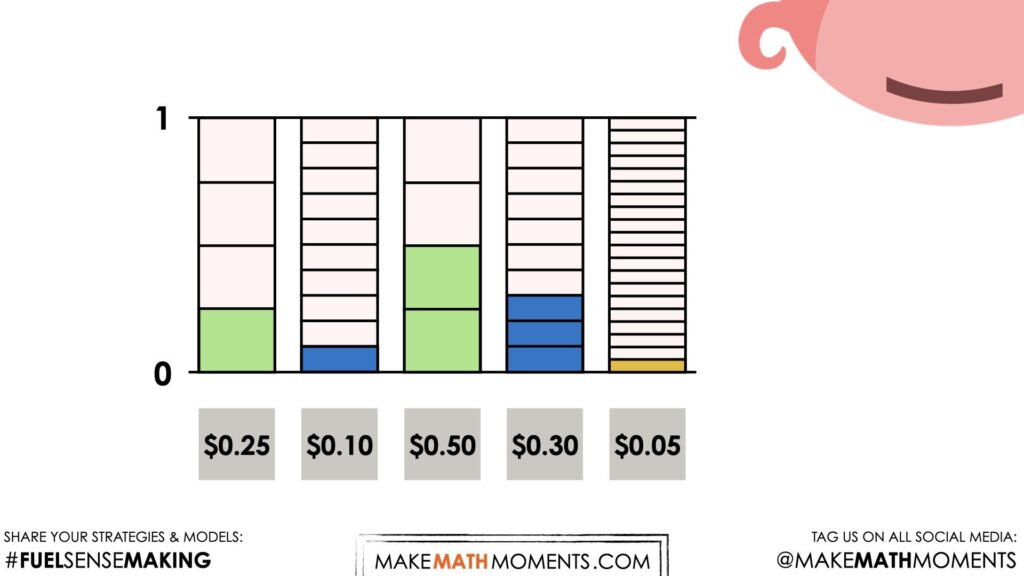
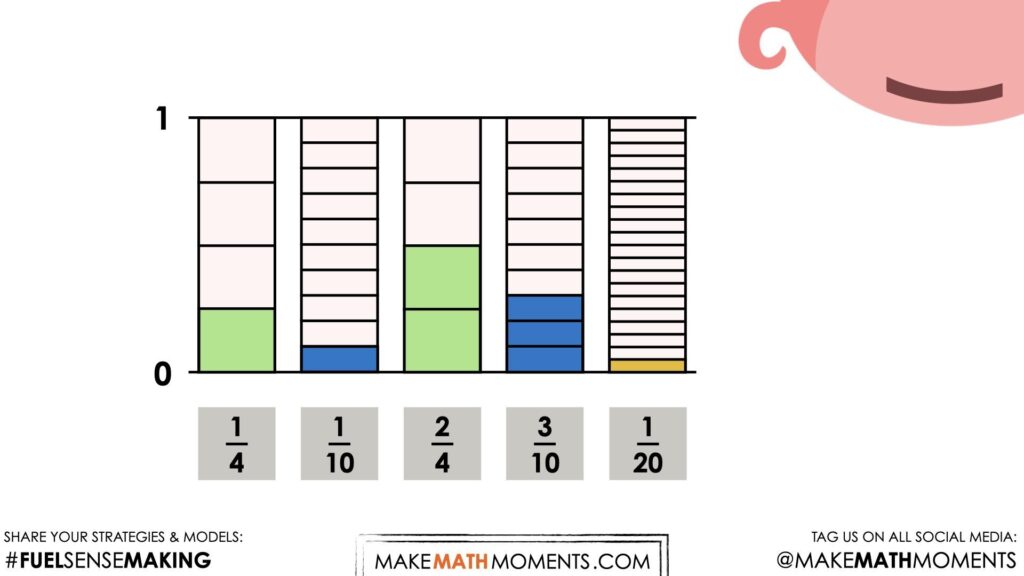
Students will first be prompted to think about:
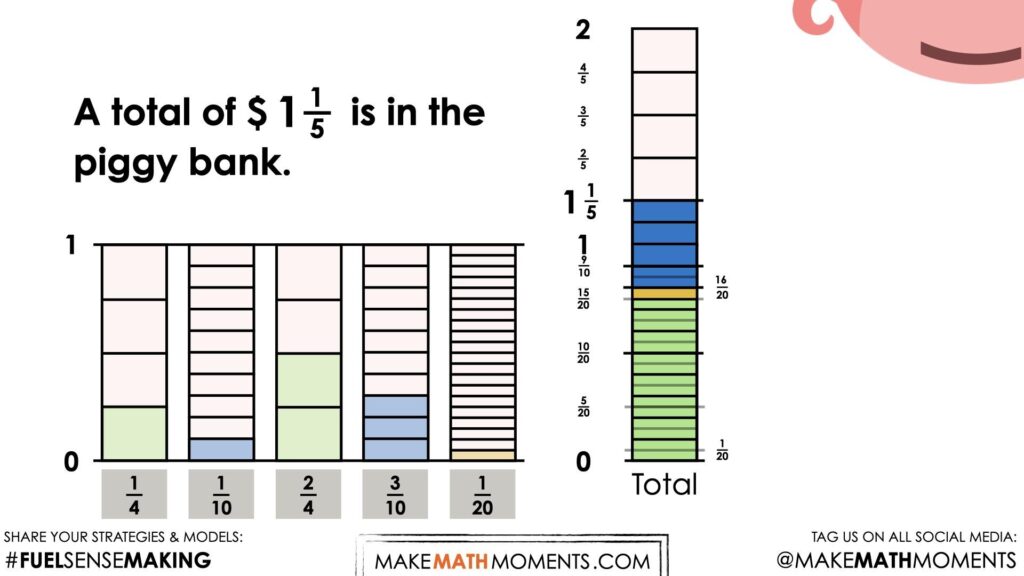
How much money was in the piggy?
How could you convince your neighbour?
Encourage students to turn to their elbow partners or group members and have an open discussion about how much was in the Piggy Bank and how they could convince someone.
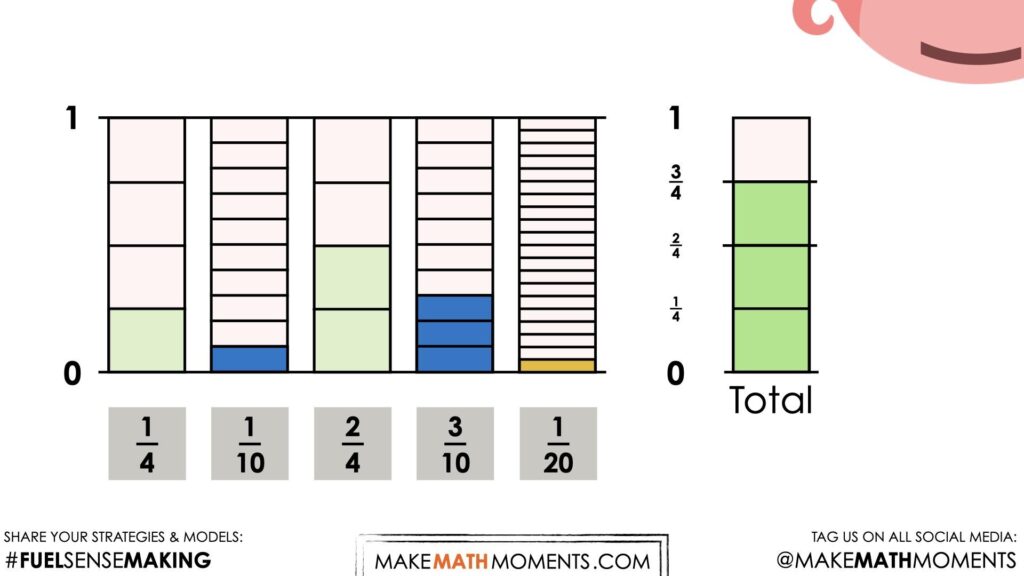
While they may (or may not) require a model to justify, we will explicitly highlight with a tape diagram (or bar model) that representing decimal values are derived from fractional amounts. While money is often written to the nearest hundredth (or 2 decimal places), we can “think” of these decimal amounts with more friendly denominators (or sizes of each piece).
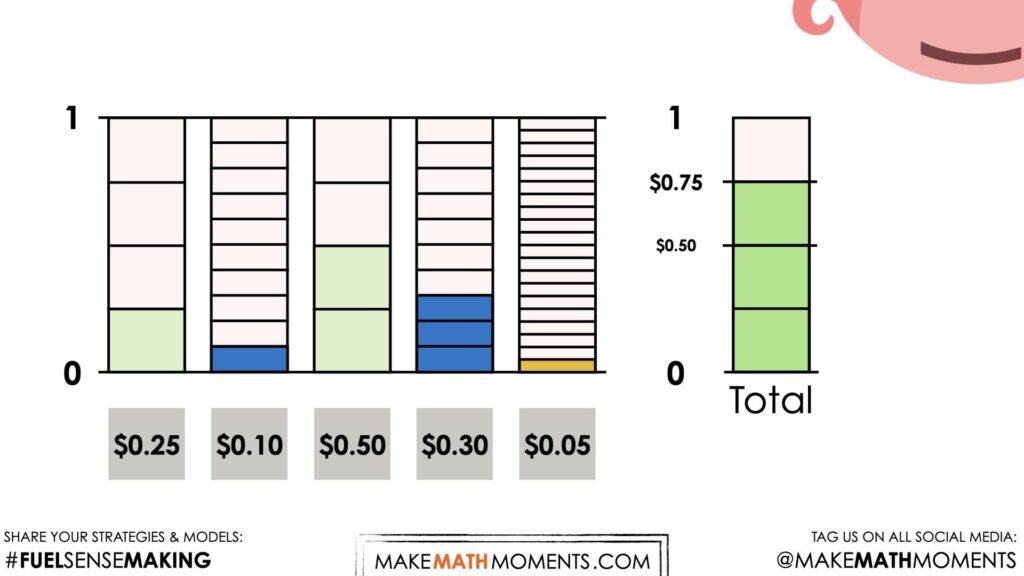
While some students may already have some automaticity for counting change (i.e.: knowing that 1 x $0.25 piece and 2 x $0.25 pieces is equivalent to 3 x $0.25 pieces or $0.75, we can help them make the connection that what they have done is added “3 fourths” or “3 quarters” as a means to highlight fraction and decimal equivalence.
Although some students may have already found the total amount of money from the Piggy Bank, consider asking students which coins they might add to the total next?
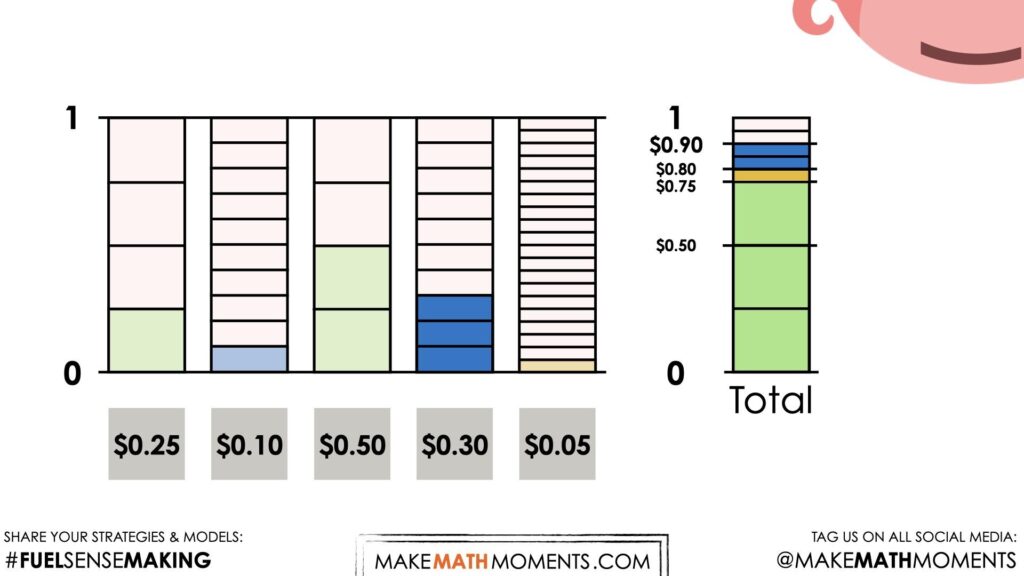
Students may have done this in their head or by using their known facts (i.e.: knowing that $0.75 + $0.10 = $0.85), it is helpful to model their thinking either by sharing the visuals from the video or actually facilitating their approach using a tape diagram or bar model.
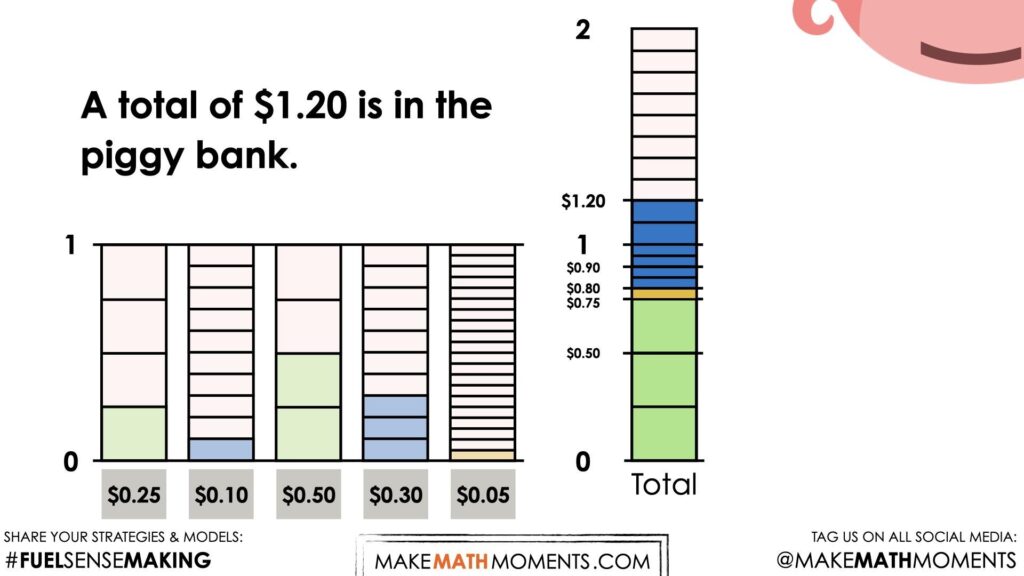
Regardless of how students go about finding the total amount of money from the Piggy Bank, our goal here is to highlight fraction and decimal equivalence as well as introducing them to a mathematical model that has linear and area characteristics that might be helpful for more difficult sums of money (or other fraction and decimal addition situations).
Visual Math Talk Prompt #2
Begin playing the video and be prepared to pause where indicated.
Students will first be prompted to think about:
How much money was in the piggy?
How could you convince your neighbour?
As the facilitator, note that this sum of money coming from the Piggy Bank is the exact amount of money that was in the Piggy Bank for Visual Number Talk Prompt #1. Students (and even educators) may not recognize this immediately unless we are looking for it.
Encourage students to turn and talk to convince their neighbour.
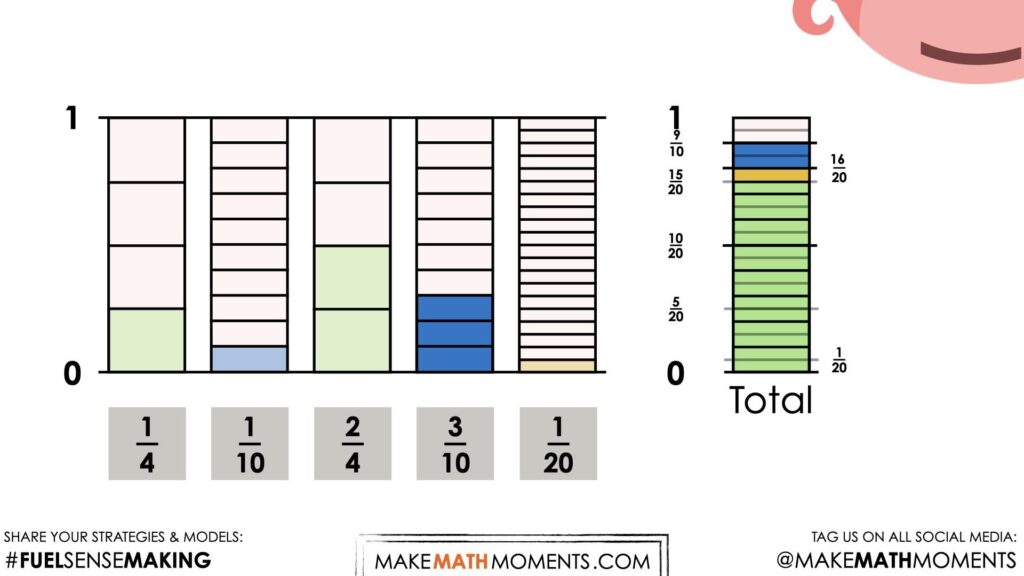
If you modelled student thinking from the first visual number talk prompt, students may leverage that model to recognize that each fractional amount looks exactly same as the decimal quantities we summed previously.
If students do not recognize that these values are equivalent, encourage them to model their thinking leveraging a tape diagram / bar model to help them determine the total sum.
As students engage in this work, be sure to highlight to students how adding fractions is much like adding decimal amounts. If we have a clear visual in our mind of what each fractional amount represents, then they are easy to add.
In the decimal situation, we are already working with a common unit fraction (or a common denominator) of hundredths whereas in this prompt, we are working with different unit fractions (fourths, tenths, twentieths, etc.).
Our goal here is to build our fluency and flexibility with fraction and decimal equivalence so that we can easily switch between these representations instead of reaching for a calculator.
Note that it is helpful to have students “stick with” fractions rather than converting to decimal as our goal here is to help students see that adding fractions can be done without mindlessly following steps and procedures to find a common denominator without thinking about what we are actually doing.
Visual Math Talk Prompt #3
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Visual Math Talk Prompt #4
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Purposeful Practice
While Students Are Practicing…
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Students will have an opportunity to independently complete practice questions related to representing and adding fractions and decimals.
As students are working, you might consider using this opportunity to pose purposeful questions and document student thinking for the purpose of formative assessment.
Pay close attention to the strategies that students are using.
Are students:
- Paper folding?
- Partitioning an area or bar model?
- Finding a common denominator (100)?
- Partitioning a number line?
- Using benchmark fractions?
While students are working independently, you might also consider strategically pulling students individually or in small groups to offer guided instruction in order to move them along their developmental continuum.
Questions: Working With Fractions & Decimals
Allow students the opportunity to engage in purposeful practice without the use of a calculator to promote their fluency and flexibility with these concepts and to model their thinking:
Question #1:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #2:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #3:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #4:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Facilitator Note:
The fourth question was created to help students to begin recognizing that representing fractional quantities as a decimal is not as helpful when the denominator (or unit fraction) is not a factor or multiple of 100.
For example, representing halves and fourths is more convenient than representing thirds and sevenths since 2 and 4 are factors of 100, while 3 and 7 are not.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Download Editable/Printable Handout
Become a member to access purposeful practice to display via your projector/TV, download the PDF to upload to your LMS and/or print for students to have a physical copy
Resources and Downloads
Lesson Tip Sheet

Download the lesson plan in PDF format so you can keep it handy and share with colleagues.
Videos & Images
 Download the videos, images, and related media files to your computer to avoid streaming.
Download the videos, images, and related media files to your computer to avoid streaming.
Keynote Slides
 Download in Apple Keynote format to avoid streaming video and run the lesson smoothly.
Download in Apple Keynote format to avoid streaming video and run the lesson smoothly.
PowerPoint Slides
 Download in Microsoft PowerPoint format to avoid streaming video and run the lesson smoothly.
Download in Microsoft PowerPoint format to avoid streaming video and run the lesson smoothly.
Printable Handout

Download/edit the handout so you can keep it handy and share with colleagues.
Explore The Entire Unit of Study
This Make Math Moments Task was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, and extensions to elicit and emerge mathematical models and strategies.
Click the links at the top of this task to head to the other related lessons created for this unit of study.
Visual Math Talk Prompt #1
Visual Math Talk Prompt #2
Visual Math Talk Prompt #3
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Visual Math Talk Prompt #4
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
1. Complete the…
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
2. Gabby heads to…
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
3. Use a model to…
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
4. Reflect…
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Download Editable/Printable Handout
Become a member to access purposeful practice to display via your projector/TV, download the PDF to upload to your LMS and/or print for students to have a physical copy