PIGGY BANK
ADD, SUBTRACT AND MULTIFLY FRACTIONS AND DECIMALS
Understand the relationship between fractions and decimals, add and subtract fractions and decimals, and multifly fractions and decimals by whole numbers.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview
Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
As coins are dropped into the piggy bank, consider how the meter increases. Based on the increase relative to the whole one dollar, predict the value of each coin and determine the total amount of money deposited in the bank.
Intentionality…
In this task, students explore the relationship between fraction and decimals. In particular, we will explore the equivalence between coins, expressed as fractions of a whole dollar, and their corresponding decimal representation. The purpose of this lesson is to encourage students to think flexibly about these two representations.
When operating with fractions and decimals, at times, it will be more convenient to think of the fraction as a decimal, and vice versa.
All tasks within this unit are intended to be completed without the use of a calculator to support reasoning and thinking.
Some of the big ideas that will likely emerge in this task include:
- Fractions can be represented in a variety of ways;
- Fractions (and their decimal representation) represent values relative to a whole (for example, one whole dollar);
- Quantities represented as a decimal are fractions limited to base ten denominators (i.e.: tenths, hundredths, thousandths, etc.);
- Standard representation of coin values are expressed as decimal hundredths.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group. Be sure to write down these noticings and wonderings on the blackboard/whiteboard, chart paper, or some other means to ensure students know that their voice is acknowledged and appreciated.
Some of the noticing and wondering that may come up includes:
- I notice a piggy bank.
- I notice a bar on the side.
- I notice that every time the person drops a coin, the bar goes up.
- I notice he dropped money in the piggy bank seven times.
- I notice the bar goes from 0 – 2.
- I wonder why.
- I wonder if there was already money in the bank.
- I wonder what the black bar means.
- I wonder how much money is in the piggy bank.
At this point, you can answer any wonders that you can cross off the list right away. For this particular lesson, you will want to keep most of the information hidden at this time. By sharing too much information, you may rob students of their thinking. One thing you can confirm is that the piggy bank was empty before the first coin was deposited.
Estimation: Prompt
After we have heard students and demonstrated that we value their voice, we can land on the first question we will challenge them with:
How much money is in the piggy bank?
Make an estimate.
We can now ask students to make an estimate (not a guess) as we want them to be as strategic as they can possibly be. This will force them to use spatial reasoning alone to try and come up with an initial estimate and to share it with their neighbours by trying to articulate why they believe their prediction is reasonable.
Consider asking students to think about a value that would be “too low” and a value that would be “too high” before asking for their best estimate in order to help them come up with a more reasonable estimate.
Let them chat with their neighbours and challenge them to an estimation duel or a math fight.
While Students Are Estimating…
Monitor student thinking by circulating around the room and listening to the mathematical discourse.
Encourage students to use precise mathematical language. You will likely hear students discussing coins using the names of the coins (quarter, dime, nickel), as well as the number of cents. Based on the movement on the meter, pay close attention to the use of fractional language.
For example, “I think the meter increased to one-tenth between 0 and 1”.
After students had an opportunity to share their best guess, tell them that you will share some information with them that might help to refine their estimate.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Show students the following image:
Prompt students with:
Based on the meter readings for all seven coins, determine the value of each coin, and the total amount deposited in the piggy bank.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Paper folding
- A pictorial representation such as a bar model
- A number line
- An area model
- Equivalence
- Common denominator
Have students share their strategies and reasoning for how to represent each coin and the total value of coins in the piggy bank. Ask them to convince you and their peers that their answer is correct by sharing mathematical models.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
Student Approach #1: Paper Folding
I cut strips of paper like the meter. I saw that the first one was one-fourth. I know that one dollar split into four parts is 25 cents. There were two one-fourths, so I coloured in two 25 cents.
There was one whole dollar, and two whole dollars, so I coloured those in also. Then I saw there were two that were cut into ten parts. When you split one dollar into 10, its 10 cents, because 10 x 10 is 100. I coloured in two ten cents. Then I saw the one that was cut into twenty parts. It was hard to fold my paper into twenty parts, but I know that if I break each of the tens in half, that will make twenty, so I coloured in half of a tenth, that’s 5 cents more. Then I added them up, $3.75.
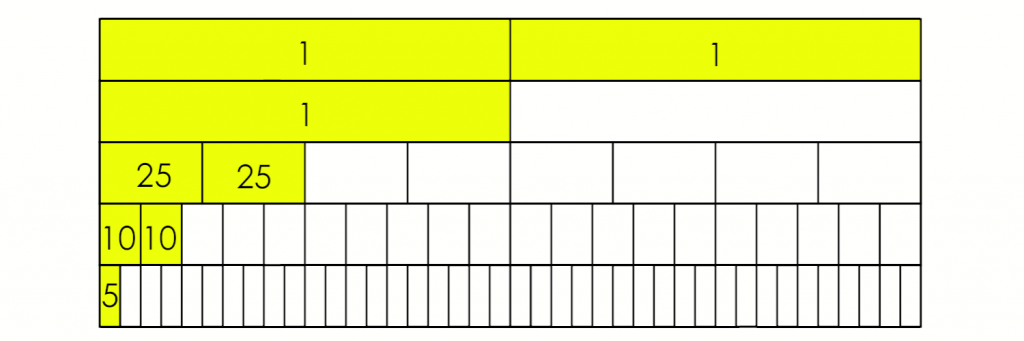
Student Approach #2: Fraction Tower
I used a table in Word. I decided to start with the largest coins, and then work my way down. I knew that they added a toonie, and then a loonie. I also saw that two of the coins were partitioned into fourths.
I know that 4 quarters make one dollar, so I added two 25 cents. I also saw that two meters were cut into 10 pieces. I know that those are dimes, because 10 dimes makes one dollar. The last one, the smaller value was cut into 20 parts. If 10 parts is a dime, then 20 must be a nickel. So I added 5 cents. In total, they put 3 dollars and 75 cents into their piggy bank.
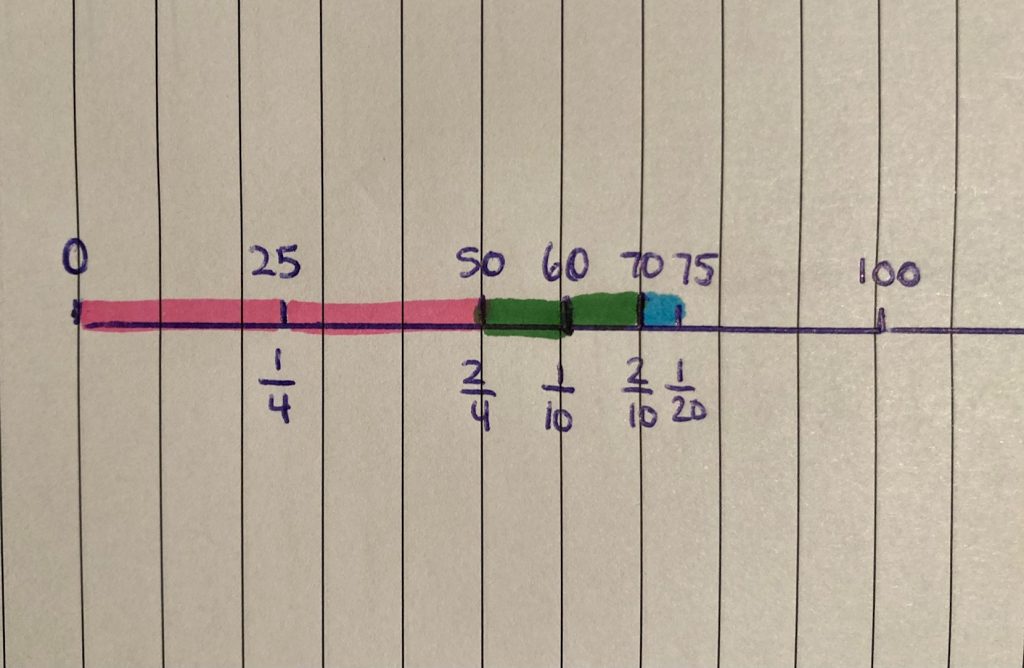
Student Approach #3: Double Number Line Using Benchmark Fractions and Equivalence
I know that one of the coins is $1.00, and another coin is $2.00. I decided to focus on the remaining coins. I drew a number line.
At first I wasn’t sure how to partition it, then I noticed that one of the coins was cut into ten parts, I thought that might be friendly. I started with the larger coins. It went one-fourth of the way between 0 and 1, so I know those are quarters, that would get me to half of a dollar, or 50 cents.
Then I had the two coins that went to one-tenth. Because my number line is cut into ten parts, I just added two more parts (which is the same as adding 20 cents because 100 split into ten parts is 10 cents in each part). I was left with the smallest value coin. It only went one of twenty parts, I know that is half of ten, such it must be a nickel, 5 more cents.
The total value is $3.75.
Next Moves
Reveal
Show this video that empties out the piggy bank to reveal the coins:
Or consider sharing this image of the final frame of the video here:
![Piggy Bank [Day 1] - MMM Slide Deck.001](https://learn.makemathmoments.com/wp-content/uploads/2021/01/Piggy-bank-Day-1-06-Reveal-Coins-image.png)
Consolidation
Through today’s consolidation, the intention is to reveal the relationship between benchmark fractions and the equivalent decimal (expressed as dollar values). Having a firm understanding of this relationship will be helpful when students operate with some fractions and decimals; to think of them as money (or coins) when appropriate.
Collaboratively investigate the coins included in the video and their equivalent representations.
For example, one quarter = \(\frac{1}{4}\) = \(\frac{25}{100}\) = 0.25. Use an appropriate model such as a bar model to represent these values.
Consider prompting students with:
Consider the dimes in the video.
There were two dimes dropped into the piggy bank.
How can we represent this quantity?
Allow students to share and ensure that a connection is made between the different fractional and decimal representations:
\(\frac{1}{10}\) + \(\frac{1}{10}\) = \(\frac{2}{10}\) or \(\frac{20}{100}\) or 0.20 or 20 cents or (2 x 0.10)
Share strategies for determining the total value. For example, did students collect the quarters? The dimes?
Facilitator Note:
This idea of collecting “like coins” might remind you, or students of collecting “like terms”. This might be an opportunity to introduce this idea from algebraic reasoning in an accessible and logical way.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt:
Consider the addition sentence below:
\(\frac{3}{4}\) + \(\frac{2}{10}\) + \(\frac{1}{20}\) + 1
What coins could be used to represent each fraction?
What is the total value?
How can you convince someone?
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!
