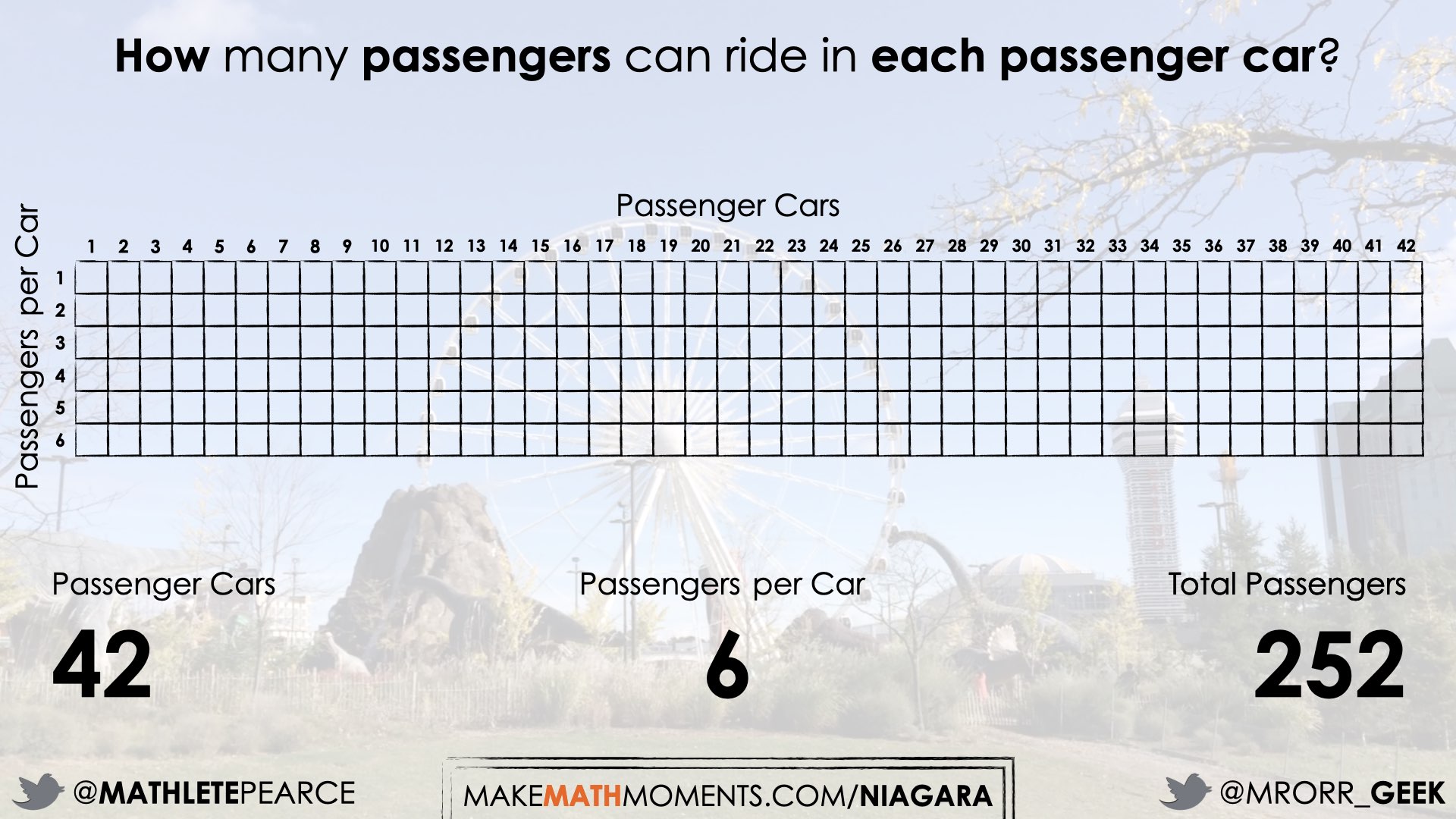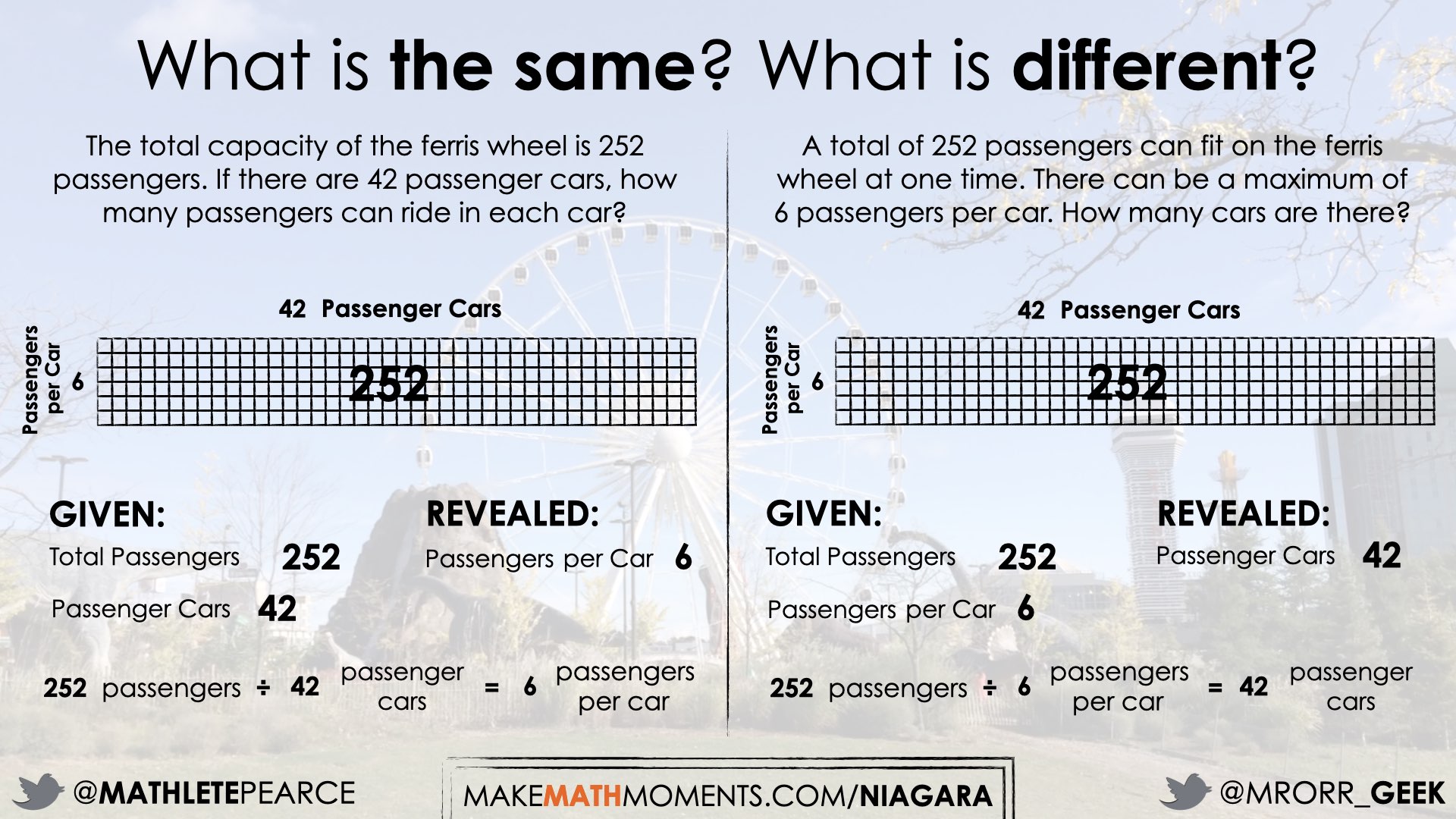NIAGARA FALLS
EXPLORING PARTITIVE & QUOTATIVE DIVISION WITH WHOLE NUMBERS
Investigate the two types of division through the exporation of tourist attractions in Niagara Falls, Ontario.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will explore the number of passengers per car, and the total number of cars on the ferris wheel through partitive and quotative division.
Intentionality…
In this task, students will determine the total number of passenger cars, and the numbers of riders per passenger car on the featured SkyWheel ferris wheel in Niagara Falls, Ontario. This task serves to highlight the difference between the two types of division; partitive and quotative.
Some of the big ideas that will likely emerge in this task include:
- Multiplication and division are related.
- There are two types of division.
- Partitive division reveals a rate.
- Quotative (or measured) division reveals the numbers of parts when the rate is known.
- The dividend from any division sentence can be decomposed into smaller parts to allow for friendlier division by the divisor. This strategy is known as partial quotients. (i.e.: 85 ÷ 5 = 45 ÷ 5 + 40 ÷ 5 = 9 + 8 = 17)
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Replaying the video and/or leaving a screenshot from the video up can be helpful here.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group. Be sure to write down these noticings and wonderings on the blackboard/whiteboard, chart paper, or some other means to ensure students know that their voice is acknowledged and appreciated.
Some of the noticing and wondering that may come up includes:
- I notice a ferris wheel
- I wonder if this is at a fair
- I wonder how tall it is
- I wonder how many people can ride at the same time
- I wonder how many people can ride together
- I wonder how much it costs to ride
At this point, you can answer any wonders that you can cross off the list right away. For example:
- This ferris wheel is in Niagara Falls, Ontario, Canada;
- It costs $12.99 for adults to ride, and $6.99 for children; and,
- It is 53 metres tall.
Estimation: Prompt
After we have heard students and demonstrated that we value their voice, we can land on the first question we will challenge them with:
How many passengers can ride this ferris wheel at one time?
Make an estimate.
We can now ask students to make an estimate (not a guess) as we want them to be as strategic as they can possibly be. This will force them to determine a number of passengers that would be reasonable before determining a more precise answer.
Consider asking students to think about a number of passengers that would be “too low” and a number that would be “too high” before asking for their best estimate in order to help them come up with a more reasonable estimate. Encourage students to share their estimates, however avoid sharing their justification just yet. We do not want to rob other students of their thinking.
Estimation: Partial Reveal & Update
Reveal the total number of passenger cars by showing this short video clip:
Alternatively, you could show this screenshot from the final frame of the video:
Now that students know the total number of passenger cars on the ferris wheel, you can prompt them to update their estimates by stating something like:
Now that you know there are 42 passenger cars, how does this impact your original estimate? Consider reflecting on your original estimate and determine whether you think it is still reasonable. You can also consider updating your estimate, if you’d like.
Give students an opportunity to revise their estimates.
Facilitator Note:
Be sure to reiterate that we are not leveraging the help of a calculator here as we are always trying to give students an opportunity to build their fluency and flexibility with operations by leveraging strategies and mathematical models – in this case, for multiplication.
While Students Are Revising Estimates
Listen and observe as students work to make updates to their original estimates. Are students aware that multiplication or repeated addition will help them come up with a more precise estimate by selecting a reasonable rate for the number of people per passenger car?
What strategies and mathematical models are students leveraging? Are they:
- Skip counting by their estimated rate of people per passenger car?
- Utilizing partial products through a drawn area model?
- Using multiplicative thinking as they make jumps on a double number line?
- Using an algorithm?
Making note of where students are developmentally as they work through this multiplication problem and ensure that you prompt them to explain why they believe their strategy is going to work to come up with a more precise total number of passengers that can ride on the ferris wheel at one time.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Acknowledge students’ estimates and consider doing a mini-consolidation of multiplication strategies and models students used as tools for thinking or tools to represent their thinking.
By doing this, you will not only show students that you value their voice and their thinking, but also have an opportunity to highlight multiplicative strategies and models that may be helpful as we prepare to dive into the actual intentionality of this lesson.
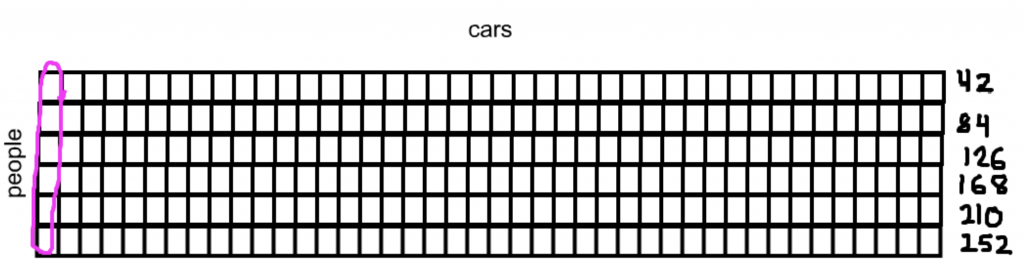
Share that 252 passengers can ride at one time assuming all 42 passenger cars are full.
Celebrate student estimates that were very close to the actual number of riders using a routine of your choice as we head into the sense making portion of this lesson.
Prompt students by stating:
The total capacity of the ferris wheel is 252 passengers. If there are 42 passenger cars, how many passengers can ride in each car?
Use a mathematical model of your choice to defend the maximum number of passengers per car that can ride on the SkyWheel ferris wheel.
Be sure to remind students that they are not to use a calculator to determine the number of passengers per car as using that tool will rob them of this mathematical experience.
Also be sure to ask that students don’t shout out answers – especially since students who were close with their estimate may now have a number close to the number of passengers per car. Rather, we want students to ensure that they have a mathematical model that will be useful for convincing others in the class.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Concrete manipulatives to fairly distribute the people between 42 cars.
- An array through skip counting
- An open-array using partial products
- A flexible algorithm using partial products
Have students share their strategies and reasoning for how to represent the number of passengers per car. Ask them to convince you and their peers that their answer is correct by sharing mathematical models.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
Student Approach #1: Fair Sharing Concretely
I started with 252 tiles. Those are the people on the ferris wheel. Then I made 42 piles. Each pile is one car. When I handed out all of the tiles to the 42 cars, I ran out of tiles when every car had 6 passengers.
Student Approach #2: Array Using Repeated Addition
I created a row of 42. I imagined that in this situation, those are the 42 cars, and every car has one person. That wasn’t enough. So I added another row, now every car has two people. I added 42 + 42, but that was only 84. So I kept adding another person, and adding 42 more. I did this six times, and when I added 42 for the sixth time, there were 252 people on the ferris wheel.
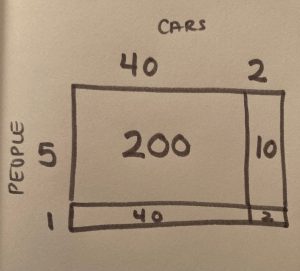
Student Approach #3: Open-Array Using Partial-Products and Revealing Partial-Quotients
I know that the total number of passengers is 242. I figured that there were at least 5 people in each car, and 5 is an easy number for me to multiply with. I know to get a total of 242, I have to multiply the 42 cars by the number of passengers on each car.
I decided to multiply by 40, and then by 2 because that is easier for me. I multiplied 5 people by 40 cars, which is 200, and 5 people by 2 cars, which is 10. I realized if I added one more person to every car, I would have 42 more passengers, and that would give me a total of 252. Therefore, there must be 6 people in each car.
Next Moves
Consolidation
As you are highlighting your sequenced student solutions, now is your opportunity to name the operator.
Prompt:
What operation did you use to solve this problem?
Give students the opportunity to turn and talk, and then share some of their thinking.
At this point, students may or may not have realized that they were using division.
252 ÷ 42.
During the consolidation, highlight the array model by selecting a student solution that leveraged an array or similar such as we see in Student Approach #2. If there are no student solutions where this model was used, select a student strategy that lends itself to the use of an array model and highlight their thinking using an array.
Facilitator Note:
The array model will be an important tool as students navigate the rest of this unit, so making an intentional teacher move to leverage the array here is very important and helpful.
Here’s a short silent solution animation video that can help with planning and delivering your consolidation utilizing the array model:
Here’s a screenshot of the last frame of the animation:
Clearly communicate both orally and in written form the information that was known and unknown in this problem.
Given:
The total number of passengers (252)
The total number of passenger cars (42)
Revealed:
The number of passengers per car
Reinforce that this scenario can be represented as:
252 passengers ÷ 42 cars = 6 passengers per car
Ask students to consider the following scenario:
A total of 252 passengers can fit on the ferris wheel at one time. There can be a maximum of 6 passengers per car. How many cars are there?
Ask students to compare the problem that was solved today to this second scenario by asking:
What is the same and what is different?
Give students time to discuss with their neighbours, model the second scenario and compare before sharing what they notice with the group.
Consider posing purposeful questions that will encourage students to organize what is given and what we are being asked to reveal in each of the scenarios such as:
- What information is being shared in each scenario?
- What information are we hoping to reveal?
- How is the information the same and how is it different?
Watch the following silent solution animation that unpacks the two similar, but different scenarios and how one might go about solving with an array model:
Together, write this scenario as a division sentence.
252 passengers ÷ 6 passengers per car = 42 passenger cars
Use the array to compare the two scenarios. Highlight in the second context what is known and what is unknown.
It is important for students to note that in the second scenario, two pieces of information swap between the information given and information we are being asked to reveal:
Given:
The total number of passengers (252)
The number of passengers per car (6)
Revealed:
The number of cars.
Ensure students have recognized that while these two scenarios require division to reveal the information asked for in each problem, the approach to finding the quotient is quite different. We can say that when dividing, there are two types or structures:
Partitive division takes place when a context requires the partitioning of a quantity into a specified number of parts or groups. The quotient revealed is the measure or quota of each group, known as a rate.
Quotative (or measured) division, on the other hand, takes place when a context requires a quantity to be organized into parts with a specified rate (measure or quota) in each part. The quotient revealed is the number of partitions or parts that can be created.
Facilitator Note:
While it may (or may not) be important for students to name the two types of division, we do want students to be able to notice that there are two types and the approach to operating with one type of division is very different to the approach to operating with the other type.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt:
Consider the following scenarios:
- There are 112 candy apples in total. All of the candy apples are stored in 4 boxes. How many candy apples are in each box?
- There are 112 candy apples. If there are 4 candy apples in each box, how many boxes are there?
For both scenarios above:
- What information is given?
- What information are you trying to reveal?
- Model both scenarios and solve.
Reflect:
How are these scenarios the same? How are they different?
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!