Task Teacher Guide

Be sure to read the teacher guide prior to running the task. When you’re ready to run the task, use the tabs at the top of the page to navigate through the lesson.

[accordion openall=”false”  clicktoclose=”true” state=”closed” autoclose=”false” openfirst=”true” clicktoclose=”true”]
[accordion-item title=”In This Task…”]

Students will reinforce concepts related to ratios and to explore how quantities covary by finding equivalent ratios through scaling in tandem.

[/accordion-item]

[accordion-item title=”Intentionality…”]

The purpose of Day 2 activities is to reinforce concepts from Day 1. Students will engage in a visual number talk that will encourage them to consider different ways to describe relationships between quantities and reinforce the idea of scaling in tandem to reveal equivalent ratios.

Students will also have an opportunity to complete purposeful practice that will serve to develop a deeper understanding of the following big ideas:

• A ratio is a multiplicative comparison between two or more quantities;
• There are two types of ratios; a composed unit ratio and a multiplicative comparison ratio;
• A composed unit is often (not always) a ratio with two distinct units;
• Unknown quantities in a ratio relationship are often most efficiently revealed through multiplicative thinking strategies rather than additive thinking strategies;
• A composed unit ratio can be scaled in tandem;
• Ratios can be constructed by comparing a part to its whole (part-to-whole) or comparing a part to another part of the whole (part-to-part).
• Ratios can be represented using the separator “to” or a colon “:”. Two quantities from a ratio relationship can also be represented as a quotient through the use of the division symbol “÷” or with the fraction bar.
• When you divide two quantities in a composed unit ratio through partitive division, you reveal a rate.
• Equivalent ratios are derived from the same rate;
• An infinite number of equivalent ratios can be revealed to assist in determining an unknown quantity from a ratio relationship; and,
• Ratio problems can be represented and solved using a variety of strategies, tools, and representations.

[/accordion-item]

[accordion-item title=”What You’ll Need…”]

A variety of tools for students to use to think through the problems, including, but not limited to:

• Linking cubes, Omnifix cubes or tiles
• Cuisenaire rods
• Grid paper
• Whiteboards & markers

[/accordion-item]

[/accordion]

Visual Math Talk

[accordion openall=”false” clicktoclose=”true” state=”closed” autoclose=”false” openfirst=”false” clicktoclose=”true”]
[accordion-item title=”String of Related Problems”]

The following visual math talk is a string of related problems that are crafted in a way to foster discussion and the construction of viable arguments. As such, they are open ended and have more than one possible response.

As the facilitator of the following visual math talk prompts, be prepared to notice and name the thinking students are using (i.e.: additive thinking or multiplicative thinking).

While you could simply share the first image with the prompt for students, introducing via the silent solution animations provided may be more helpful. Although each visual math talk prompt video models a possible strategy, we encourage you to represent student thinking by drawing on the board or on the screen rather than simply playing the video and ignoring the thinking of your students.

[/accordion-item]

[accordion-item title=”Visual Math Talk Prompt #1″]

Consider utilizing the following visual math talk prompt and be prepared to pause where indicated:

Prompt:

What do you notice? What do you wonder?

After students share some of what they notice and wonder about the shapes that have ‘popped’ on the screen, continue playing the video until the next prompt appears:

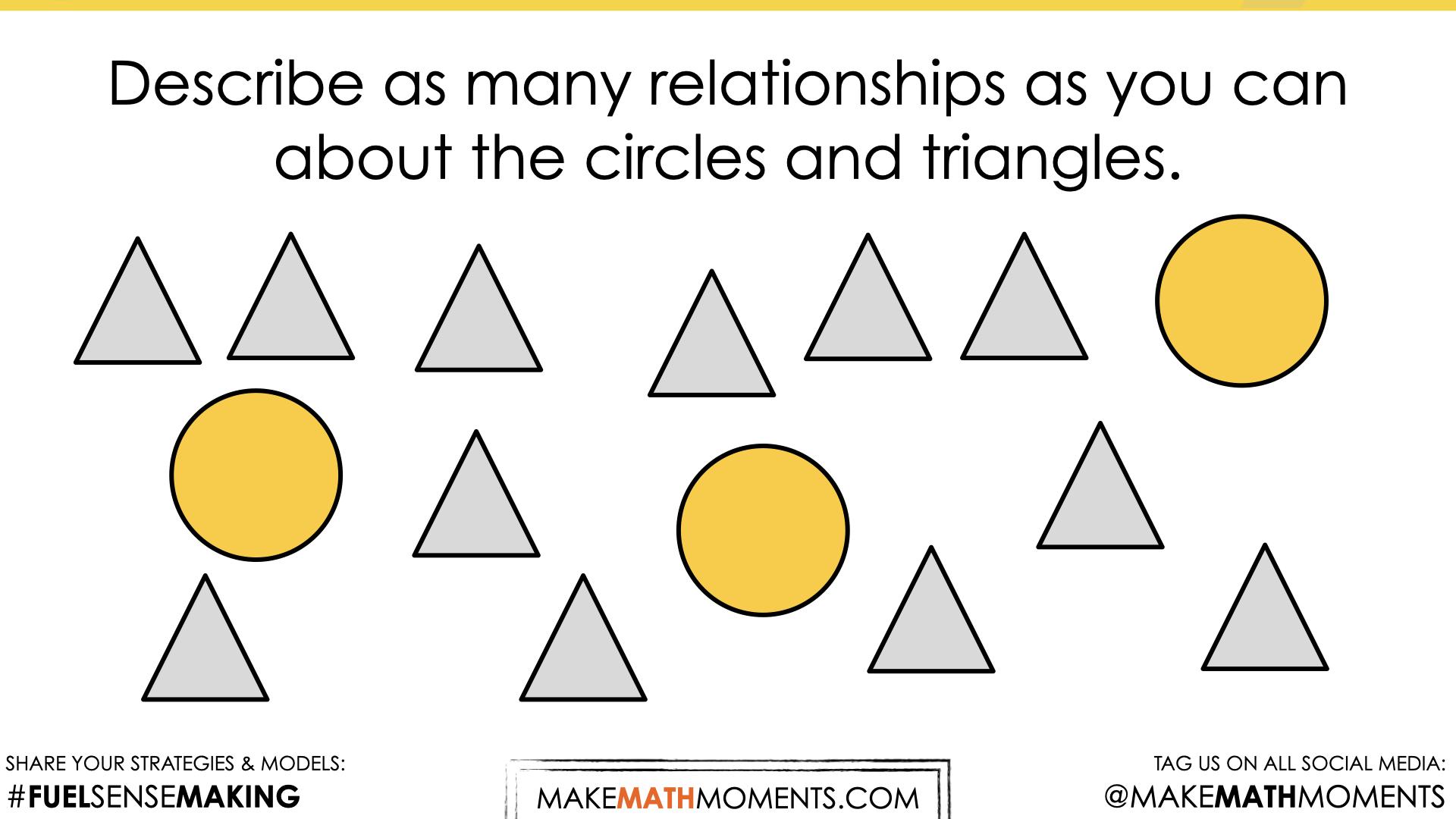
Describe as many relationships as you can between the circles and the squares.

Some possible relationships students might share include:

• There are 10 more squares than circles
• There are 3 times as many squares as there are circles
• For every circle there are 3 triangles
• \(\frac{3}{4}\) the shapes are squares (\(\frac{1}{4}\) of the shapes are circles)
• 75% of the shapes are squares

It is worthwhile to note the observations that students will share, as a way of determining if students are thinking in absolute or relative terms, and whether they are able to consider both part:whole and part:part relationships.

As you are making note of students’ observations, consider modeling the use of ratio language and notation, including:

• The ratio of ____ to ____ is _____ : ______. For example, “the ratio of squares to circles is 3:1 or the ratio of circles to squares is 1:3”.
• For every ______, there are ______.

Some students may make use of rate language such as:

• There is a rate of _____ per _____ 
• For example, “there is a rate of 3 squares per circle” or “there is a rate of 1 third circles per square”.

Of course, these are just some possible observations and many more ideas may be highlighted by your students.

Consider encouraging students to find other equivalent ratios by scaling in tandem (ratio reasoning) or by using the constant of proportionality (rate reasoning) and record their thinking in a ratio table.

[/accordion-item]

[accordion-item title=”Visual Math Talk Prompt #2″]

Consider utilizing the following visual math talk prompt and be prepared to pause when indicated:

The following prompt will appear on the screen:

Describe as many relationships as you can between the circles and the triangles.

Some possible relationships students might share include:

• There are 9 more triangles than circles
• There are 4 times as many triangles as there are circles
• For every circle there are 4 triangles
• \(\frac{4}{5}\) of the shapes are triangles (\(\frac{1}{5}\) of the shapes are circles)
• For every white triangle there are 2 green triangles

Again, consider the language students are using. Is it in absolute terms (i.e.: additive thinking) or in relative terms (i.e.: multiplicative thinking)?

If students are using multiplicative thinking, are they using ratio reasoning (i.e.: comparing squares and triangles as separate quantities) or rate reasoning (i.e.: summarizing the relationship via a single quantity with a compound unit such as 4 squares per circle”)?

After celebrating the different relationships that students may have shared using various types of reasoning, be sure to highlight again the ratio relationship via a ratio table (or double number line) and ask students to share some equivalent ratios that we can reveal from this relationship. You might also consider highlighting the constant of proportionality (i.e.: finding the rate) by using partitive division to divide the number of circles with the corresponding number of squares or visa versa from multiple rows in the ratio relationship.

[/accordion-item]

[accordion-item title=”Visual Math Talk Prompt #3″]

Login/Join to access the full Math Talk, teacher guides, downloadable slide decks and printable handouts for this lesson and all problem based units.

[/accordion-item]

[accordion-item title=”Visual Math Talk Prompt #4″]

Login/Join to access the full Math Talk, teacher guides, downloadable slide decks and printable handouts for this lesson and all problem based units.

[/accordion-item]

[/accordion]

Purposeful Practice

[accordion openall=”false” clicktoclose=”true” state=”closed” autoclose=”false” openfirst=”false” clicktoclose=”true”]
[accordion-item title=”While Students are Practicing”]

Login/Join to access the full Math Talk, teacher guides, downloadable slide decks and printable handouts for this lesson and all problem based units.

[/accordion-item]

[accordion-item title=”Purposeful Practice Problems”]

Login/Join to access the full Math Talk, teacher guides, downloadable slide decks and printable handouts for this lesson and all problem based units.

Download Editable/Printable Handout

Become a member to access purposeful practice to display via your projector/TV, download the PDF to upload to your LMS and/or print for students to have a physical copy

JOIN TO DOWNLOAD

[/accordion-item]
[/accordion]

Resources and Downloads

Explore The Entire Unit of Study

This Make Math Moments Task was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, and extensions to elicit and emerge mathematical models and strategies.

Click the links at the top of this task to head to the other related lessons created for this unit of study.