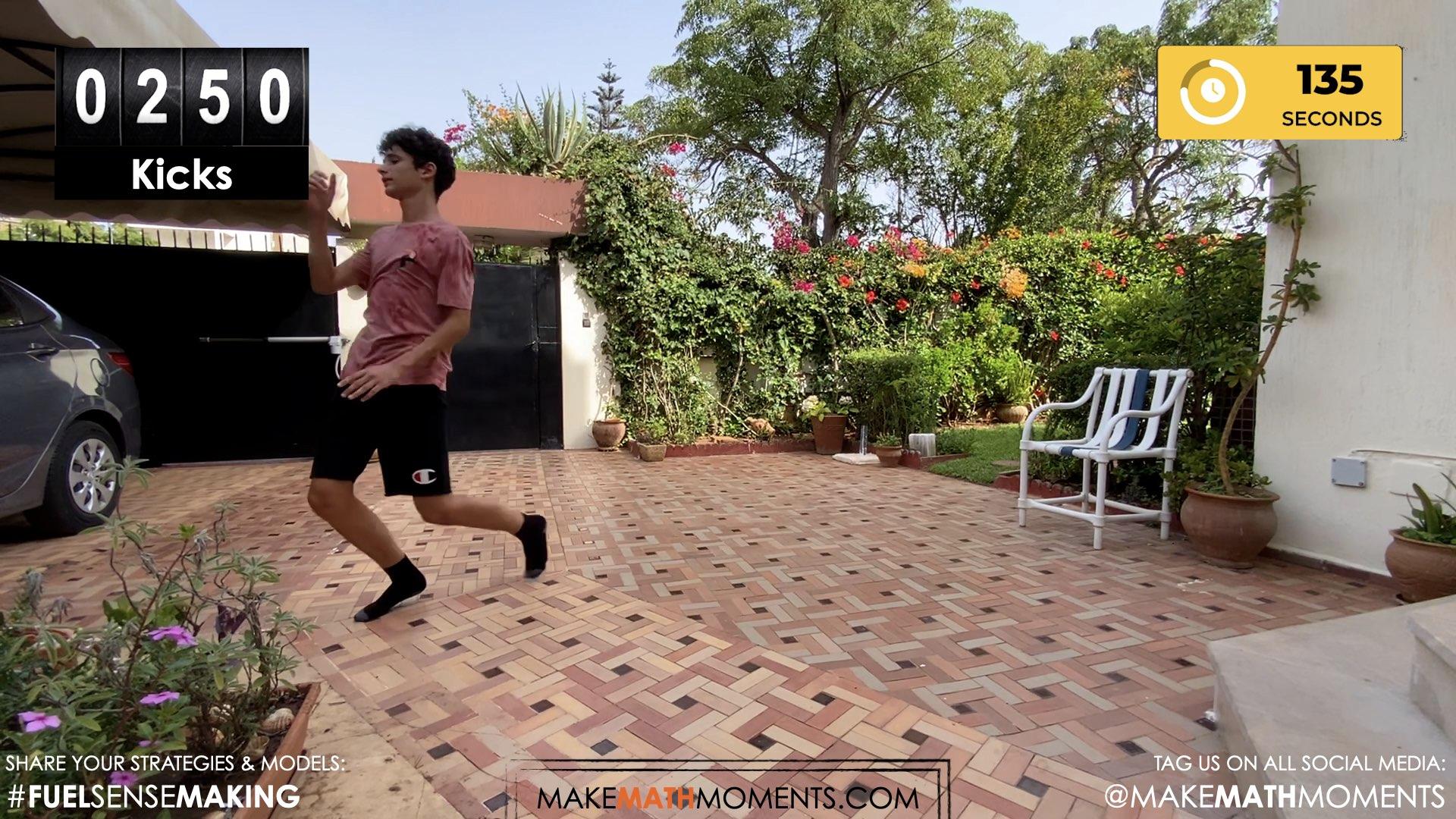KEEP IT UP
RATIOS PROPORTIONS & PERCENTS
Eyplore concepts relating to ratios, proportions and percents.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will determine how many kick ups a boy can do with a soccer ball by leveraging two quantities that covary to determine other equivalent ratios in the ratio relationship.
Intentionality…
In this task, students explore the concept of ratios and proportions through the context of a soccer player who strives to break a record of Kick Ups. This task serves as a context to bring forth a number of strategies and approaches that can be used to solve problems involving composed units.
Some of the big ideas that will likely emerge in this task include:
- A ratio is a multiplicative comparison between two or more quantities;
- There are two types of ratios; composed unit and multiplicative comparison;
- A composed unit is often (not always) a ratio with two distinct units;
- Unknown quantities in a ratio relationship are often most efficiently revealed through multiplicative thinking strategies rather than additive thinking strategies;
- A composed unit can be scaled in tandem;
- When you divide a composed unit through partitive division, you reveal a rate.
- Equivalent ratios are derived from the same rate;
- An infinite number of equivalent ratios can be revealed to assist in determining an unknown quantity from a ratio relationship; and,
- Ratio problems can be represented and solved using a variety of strategies, tools, and representations.
What You’ll Need…
A variety of tools for students to use to think through the problems, including, but not limited to:
- Linking cubes, Omnifix cubes or tiles
- Cuisineaire rods
- Grid paper
- Whiteboards & markers
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students this video:
Then, ask students:
What do you notice?
What do you wonder?
Have students do a Think-Pair-Share routine:
- Students have individual think time to jot down ideas on paper or whiteboard (minimum 1 minute). Students may benefit from watching the video a second time or having a still image from the video to refer to.
- Students share their observations and questions with a partner.
- Students share as a whole group, either their own noticings and wonderings, or a meaningful observation or question they heard from their partner during the share (while giving credit to their partner). All contributions are acknowledged and recorded on an anchor chart on the board.
Possible points that may arise include:
- I notice there’s a person playing with a soccer ball
- I wonder how many times they can kick the ball without dropping it (how many kick ups)?
- I wonder how long they can go without dropping it (how much time)?
- I notice that the person switches from his left to his right foot each time
- It looks like a nice day outside
- I wonder why he’s wearing socks and no shoes
- I wonder how long it took him to learn how to do that
Spending time to acknowledge and address specific thoughts that students shared, whether a notice or a wonder, is crucial to building a culture in your classroom where students know that their voice is being valued and thus encourages them to continue sharing their thoughts and opinions later in this lesson and in future lessons.
Estimation: Prompt
Once student noticings and wonderings have been acknowledged and noted, the class can settle on a first question to explore:
How many kick ups were completed in a row?
Make an estimate.
Students begin by making an estimate before they are provided with all the information they need to answer the question, thus requiring them to consider what would be a reasonable number of kick ups.
Encouraging students to begin by considering estimates that are “too high” and “too low” will provide a range within which more likely estimates can be framed. It can also provide students who may be reluctant to share with a safe entry point. Students can then make a “reasonable estimate”, which they will have a chance to revise.
Students should be given an opportunity to share their estimates at this point, but refrain from sharing their rationale just yet in order to give everyone a chance to develop their own thinking.
Have students turn to a partner and generate questions they could ask that would provide them with information they could use to answer the question. Ask students how they would use the information to answer the question.
Prompt:
What information would you need to answer the question?
How would you use that information?
Estimation: Partial Reveal & Update
Show students the following video sharing how many kick ups were completed in a row over a span of 5.4 seconds:
At this point, students may wish to update their estimates. Provide them with time to do so before revealing the next image. A simple prompt might be:
You’ve seen that the person does 10 kick ups in 5.4 seconds. Does this affect your estimate? Would you say your estimate is still reasonable, or will you revise it?
Provide students with time to revise their estimates.
While Students are Revising Their Estimates
Listen and observe as students revise their estimates. Are students aware that the layered structure of a rectangular prism allows them to think additively or use multiplication?
How are students approaching the problem? What strategies and mathematical models are they leveraging? Are they:
- Counting
- Basing estimates on their own experiences with soccer, juggling, or other similar activity?
- Basing estimates on the amount of time it would take to do more kick ups? (Can they keep going for a full minute? 2 minutes? 10 minutes?)
This is an opportunity to make note of where students are developmentally. Prompt students to explain their thinking and how they plan to use their model/strategy to how many “kick ups” in a row the person in the video can do.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Proceed to reveal the amount of time that the person in this video was able to keep the ball in the air:
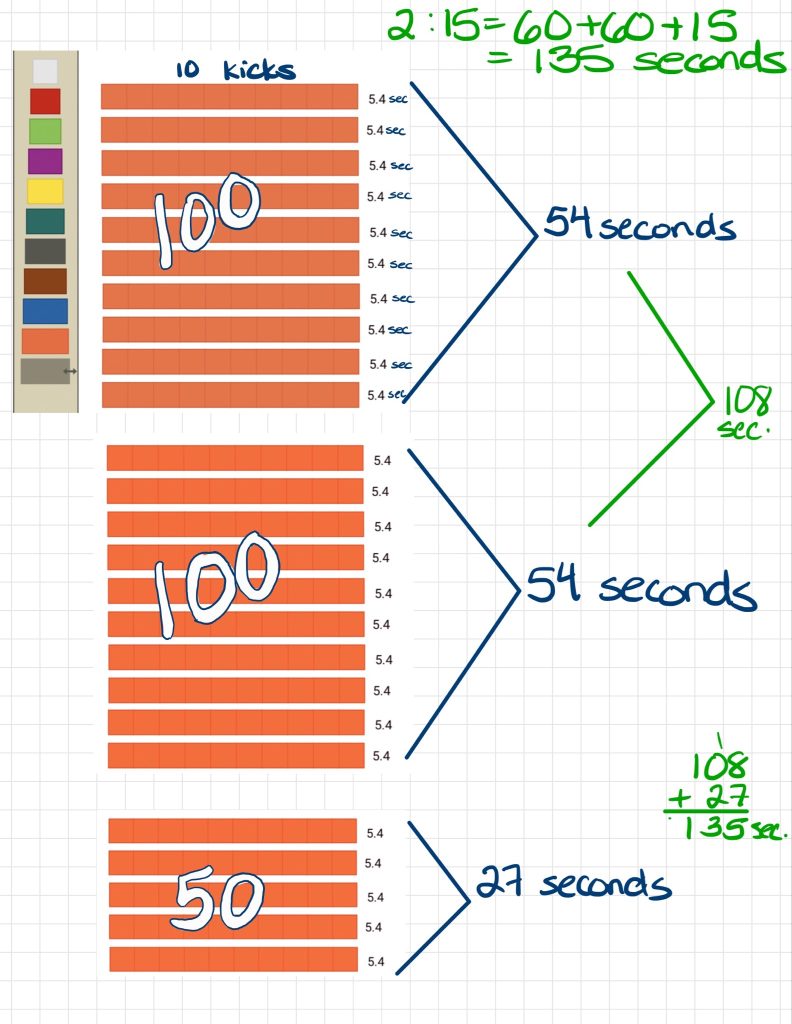
During this round of kick ups, the person in the video was able to keep the ball from hitting the ground for a total of 2 minutes and 15 seconds. If we know that the ball was kicked 10 times in 5.4 seconds, how many kick ups do you think the person did in total?
Use this information to update your estimate and craft a convincing argument using a mathematical model of your choice.
Be sure to explicitly state that calculators are not to be used to determine the number of kick ups. However, do consider making the following tools available to students without explicitly directing students to use them:
- Linking cubes, Omnifix cubes or tiles
- Cuisenaire rods
- Grid paper
- Whiteboards & markers
Remind students to refrain from shouting out answers, and be sure to emphasize the importance of creating a viable argument – a model that can be used to convince others.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include, but are not limited to:
- Concrete modeling using tiles or cubes to model each kick up/set of kick ups
- Scaling up using a visual representation
- Scaling up using repeated addition or multiplication
- Finding the rate (how many seconds per kick up) then multiplying
- Ratio table
- Double number line
Possible misconceptions and/or challenges you may consider noting include:
- Scaling the quantities in the ratio relationship by the same quantity additively, rather than multiplicatively (eg. finding the difference between 135 seconds and 5.4 seconds and applying that difference to the number of kick ups)
- Only considering one scale factor (a common example is repeated doubling)
As you circulate the room, seek to understand the strategies you are observing and work to elicit student thinking in order to provide purposeful prompts that will help them along their journey rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their current strategy and/or approach.
Student Approaches
Student Approach #1: Modeling and Scaling Using Additive Thinking
It’s easier to think about the time in seconds, so first I converted 2:15 to seconds, and that’s 135. Then I saw that there were 10 kicks in 5.4 seconds, so I used an orange rod to show that. 10 rods is 100 kicks, and that would be 54 seconds. Then I added another 10 rods which is another 54 seconds. So 200 kicks is 108 seconds. I saw that I needed a bit more to get to 135 seconds, so I added 5 more orange rods, which means 50 more kicks. 50 kicks is half of 100, so 27 is half of 54. All in all, the ball was kicked 250 times in 135 seconds.
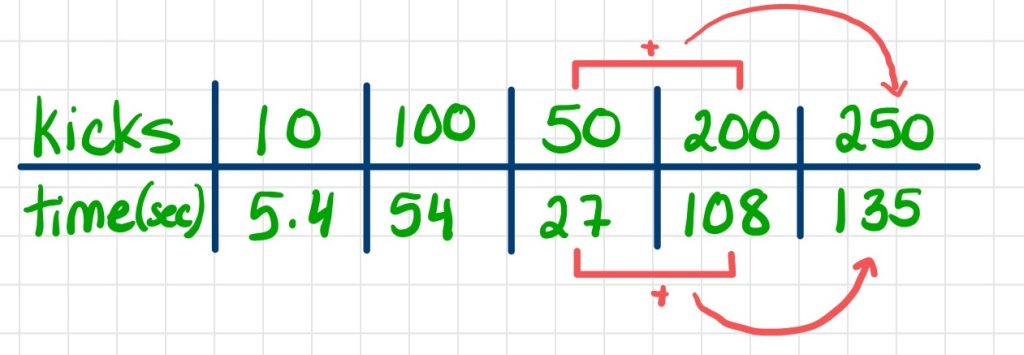
Student Approach #2: Ratio Reasoning in a Ratio Table
I made a ratio table and started with 10 kick ups in 5.4 seconds. Then I multiplied by 10 and got 54 seconds. I halved that because I thought it would be useful and 50 kick ups is 27 seconds. I doubled 100 to get 200 kick ups, which is 108 seconds. Lastly I combined 27 + 108 = 135 seconds, so that was 50 + 200 = 250 kick ups.
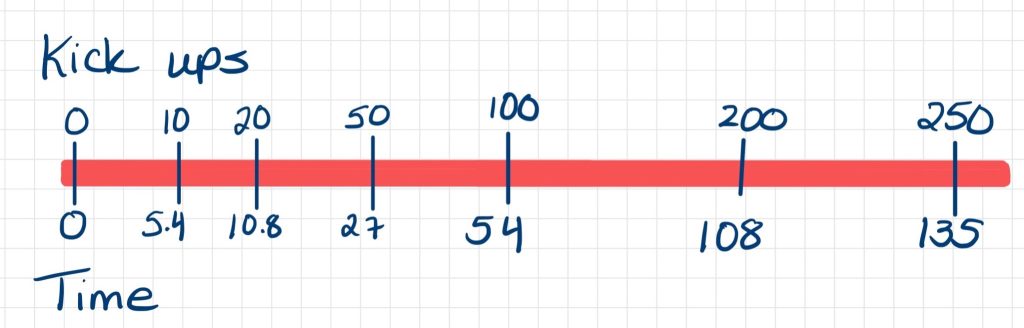
Student Approach #3: Ratio Reasoning on a Double Number Line
I made a double number line with the kicks on top and the time on the bottom. I started with what I knew, which was 10 kicks in 5.4 seconds. Then I doubled it and got 10.8 seconds. I used the time for 10 kick ups to find out how many for 50 kick ups, and then 100. I doubled 100 to get 108 seconds, but that wasn’t quite enough, so I added 27 seconds for 50 kick ups and got 250 kick ups in 135 seconds.
Student Approach #4: Rate Reasoning and Division Algorithm
If there were 10 kick ups in 5.4 seconds, that means thattheydoes 1 kick up in 0.54 seconds. So we just have to figure out how many kick ups can fit into 2 minutes and 15 seconds, or 135 seconds. I used the algorithm to divide 135 by 0.54 and got 250 kick ups. (2 different division algorithms shown)
Next Moves
Consolidation
During the consolidation, leverage student work samples and student approaches that will help you sequence from accessible approaches to approaches that will assist in emerging big ideas from this lesson.
As student approaches are shared, be sure to ask the class if they can discern how each student was thinking about the problem.
A possible prompt might be:
Can you follow the thinking of this student/group?
If not, what do you understand and what isn’t clear to you?
This encourages all students to consider alternative viewpoints and begin to seek connections between representations. It helps set up the mindset of “listening to understand” when students share their work.
Have students share their strategies and reasoning for how to represent the number of kick ups. Ask them to convince you and their peers that their answer is correct by sharing mathematical models.
One of the big ideas that is worth highlighting during the consolidation is that since we can compare the two quantities given in this problem multiplicatively (10 kick ups completed in 5.4 seconds), we are working with a ratio.
Consider prompting students with:
What were the two quantities we were comparing in this problem?
What might we call this comparison?
Since we were given a multiplicative comparison of time in seconds to number of kick ups, we can say that a ratio relationship exists and in this case, we can think of the two quantities as a composed unit ratio. This is because we can “think” of each equivalent ratio in this relationship as a single “unit” that can scale in tandem.
Be sure to highlight the different student approaches and in particular, be sure to notice and name the type of thinking being used: additive, multiplicative or a combination of both.
For example, a student who is repeatedly adding 10 kick ups and 5.4 seconds would be leveraging additive thinking. While our goal is for students to continue progressing to multiplicative thinking, note that this may be the strategy that provides that student access to this task. Therefore, honour their thinking and ask them to think about noticing how many iterations (or “copies”) of 10 kick ups and 5.4 seconds they had added. Can we also represent these copies another way (i.e.: using multiplication)?
Some students may leverage a repeated doubling strategy where they double 10 kick ups and 5.4 seconds to 20 kick ups and 10.8 seconds, then doubling again to 40 kick ups and 21.6 seconds, and so on before adding/subtracting an amount of kick ups and seconds to reveal the number of kick ups after 2 minutes and 15 seconds. A possible prompt for a student leveraging this approach might be to ask them if they could scale by more than double? If so, might there be a scale factor that might make this work easier for them?
Regardless of the type of thinking employed by students to solve this problem, be sure to highlight that all of these quantities that have been revealed through additive and/or multiplicative thinking are some of the infinite number of equivalent ratios from this ratio relationship. Through the use of the strategies and models such as those shared throughout the consolidation, we want to ensure that students understand that any unknown quantity from a ratio relationship can be found through the use of equivalent ratios.
It might be helpful to list the quantities students found to assist you in highlighting some of the equivalent ratios from this ratio relationship that were helpful to help us find the unknown number of kick ups that would correspond to 2 minutes and 15 seconds. For example, some students may have leveraged the following equivalent ratios:
| Time in Seconds | Number of Kick Ups |
| 5.4 | 10 |
| 10.8 | 20 |
| 27 | 50 |
| 54 | 100 |
| 108 | 200 |
Clearly communicate both orally and in written form the information that was known and unknown in this problem.
Given:
10 kick ups completed in 5.4 seconds
x kick ups completed in 135 seconds (2 minutes and 15 seconds)
Revealed:
The total number of kick ups completed (250) in 135 seconds
Consider viewing the following silent solution video animation to help you prepare for this consolidation and potentially support you in facilitating the consolidation:
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
If the boy hadn’t lost the ball, how long would it have taken him to do 300 kick ups? 500? 1000?
Convince your peers.
Consolidation Prompt #2:
A second set of kick ups has the ball going a little higher.
5 kick ups can be completed in 3 seconds.
How many kick ups would you expect in 1 minute?
Convince your peers.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!