GOING IN CIRCLES [DAY 4]
EXPLORING PI: CIRCUMFERENCE & AREA OF CIRCLES
Leverage contextual problems to investigate and emerge Pi to help conceptualize formulas for both the circumference and area of a circle.
Intentionality
Math Talk
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 8 Days
Access each lesson from this unit using the navigation links below
Students will explore the relationship between circumference, diameter and area of a circle by separating into congruent shapes and using their understanding of area related to other polygons (i.e.: rectangles and/or parallelograms).
In this task, students will explore the concept of area of a circle through estimation followed by measurement using non-standard units. This task will allow students to develop a deeper understanding of big ideas, including the following:
- When exploring measurement relationships of any circle, there are three (3) standard measures that can be used to reveal more information about the circle:
- Circumference: the perimeter of a circle.
- Diameter: any straight line segment beginning and ending on the outer edge of a circle and passes through its centre.
- Radius: any straight line segment beginning at the centre of a circle and ending on the outer edge of the circle.
- Knowing one of the standard measures of a circle provides information about all other measures;
- There is a multiplicative relationship between the length of the diameter and the circumference of a circle. In other words, as the diameter of a circle increases, the circumference increases multiplicatively (not additively);
- For all circles, the ratio of the circumference to the diameter is the same (approximately 22:7); and,
- For all circles, the rate of each unit of circumference length per unit of diameter length is the same (approximately \(\frac{22}{7}\) or 3.14) and is known as Pi, π.
- The area of a circle can be determined by decomposing and recomposing the figure into familiar polygons (i.e.: rectangles or parallelograms); and,
- For all circles, changing the diameter or radius will affect the area and circumference in predictable ways.
What You’ll Need…
- Pizza template of medium and large sized pizzas printed for each student;
- Non-standard measuring tools (i.e.: string, paper strips, the cord from earbuds, square tiles, grid paper, etc.);
- Scissors.
Math Talk
Students will be encouraged to explore the double number line model and apply the use of partial products made possible with the distributive property through the following string of related problems.
Leverage a circle context such as the tile circle context from day 2 or a new context. Throughout the string, each dividend represents the circumference of the circle and the divisor represents the multiplicative comparison between the diameter of a circle and the circumference (i.e.: Pi, π).
Encourage or create opportunities to represent student thinking using the double number line by pausing questions such as “would it be ok if I show your thinking using this double number line” if students do not initiate the use of a model. If students want to model their thinking another way however, this should be honoured not discouraged.
30 ÷ 3
60 ÷ 3
35 ÷ 3.5
70 ÷ 3.5
33 ÷ 3.1
Through this string, students are encouraged to see the multiplicative relationship between the circumference and diameter of a circle to make reasonable estimates when given the value of one measure with another unknown.
Facilitator Note:
You’ll notice we are providing opportunities for students to estimate rounding Pi down to 3, as well as giving some opportunities to become more precise by also using 3.5 and 3.1 to build flexibility and accuracy using mental math. For example, when dividing by a divisor of 3.5, we would discuss how Pi is actually closer to 3.14, however let’s assume the multiplicative relationship between the diameter and the circumference is 3.5; what would the diameter be in this case? In other words, we are saying “the circumference of a circle is 35 units and since I know that Pi is 3.14, using a friendly divisor of 3.5 allows for us to get pretty close without reaching for a calculator.”
The goal here is to empower students to reason through scenarios and adjust their final answer up or down depending on the divisor they selected for their mental math calculations.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Today’s problem based lesson will begin with a “Would You Rather” prompt by showing this image:
Give students time to discuss with elbow partners and/or their table groups before sharing out to the whole group.
Note that at this point, students may have different opinions and perspectives as to which option they would rather choose.
For example, some students might say:
- I’d rather have option #2 because it is less packaging and less complicated.
- Option #1 because my family likes different toppings, so we usually go with two smaller pizzas to make sure there is no “mixing” of toppings.
- Option #2 because it looks like more pizza and I love pizza!
- Option #1 because I love garlic crust and it looks like more crust.
- I think both options have the same amount of pizza, so I’m easy either way.
- And many more!
Show students you value their voice by acknowledging their thoughts and perspectives.
Estimation: Prompt
Next, begin sharing a story about what matters to you and/or your family/friends when ordering pizza. Something like this could help:
Tomas had mentioned that his family really enjoys the crust of the pizza and in my household, we are also fans of garlic even though it can sometimes leave our breath less than fresh!
So, I’m wondering if Tomas and his family are ordering pizza and they wanted the most crust…
Which option do you think will give them the most crust?
Give students some time to use their spatial reasoning to come up with an estimate that feels good to them. Encourage them to share their initial thoughts and wonders with their table groups before allowing students to share their thinking with the class as a whole.
Although the crust wraps the circumference of each pizza, you might encourage students to make other comparisons by posing purposeful questions like:
- What measurement matters if we are trying to determine which option has the most crust? (i.e.: the distance around the pizza also known as the circumference)
- Are there any other measurements that would be helpful for us to consider or compare as we come up with our initial estimates?
- I wonder how much larger the diameter of the large pizza is compared to a medium pizza?
Rather than placing too much emphasis on the estimate itself, we want to encourage students to reason through this scenario. Through this discussion, students may begin to develop more conviction as to which they believe will result in the most crust.
Facilitator Note:
Listen to students as they discuss with their table groups. Are any students making a connection to our previous work related to the multiplicative relationship between the diameter and circumference of a circle we now know as Pi, π? This is an excellent formative assessment opportunity to inform you of where students are related to this very important concept. Often times, educators believe that connections from previous lessons are solidified when in actuality, they are not. It is very possible that students require more explicit exploration and consolidation of the relationship between the diameter and the circumference than you may have anticipated.
After students have been given adequate time to turn and talk to share with their peers, encourage students to begin sharing out their own thinking or what they are hearing from others to the math community as a whole.
Update Your Estimate
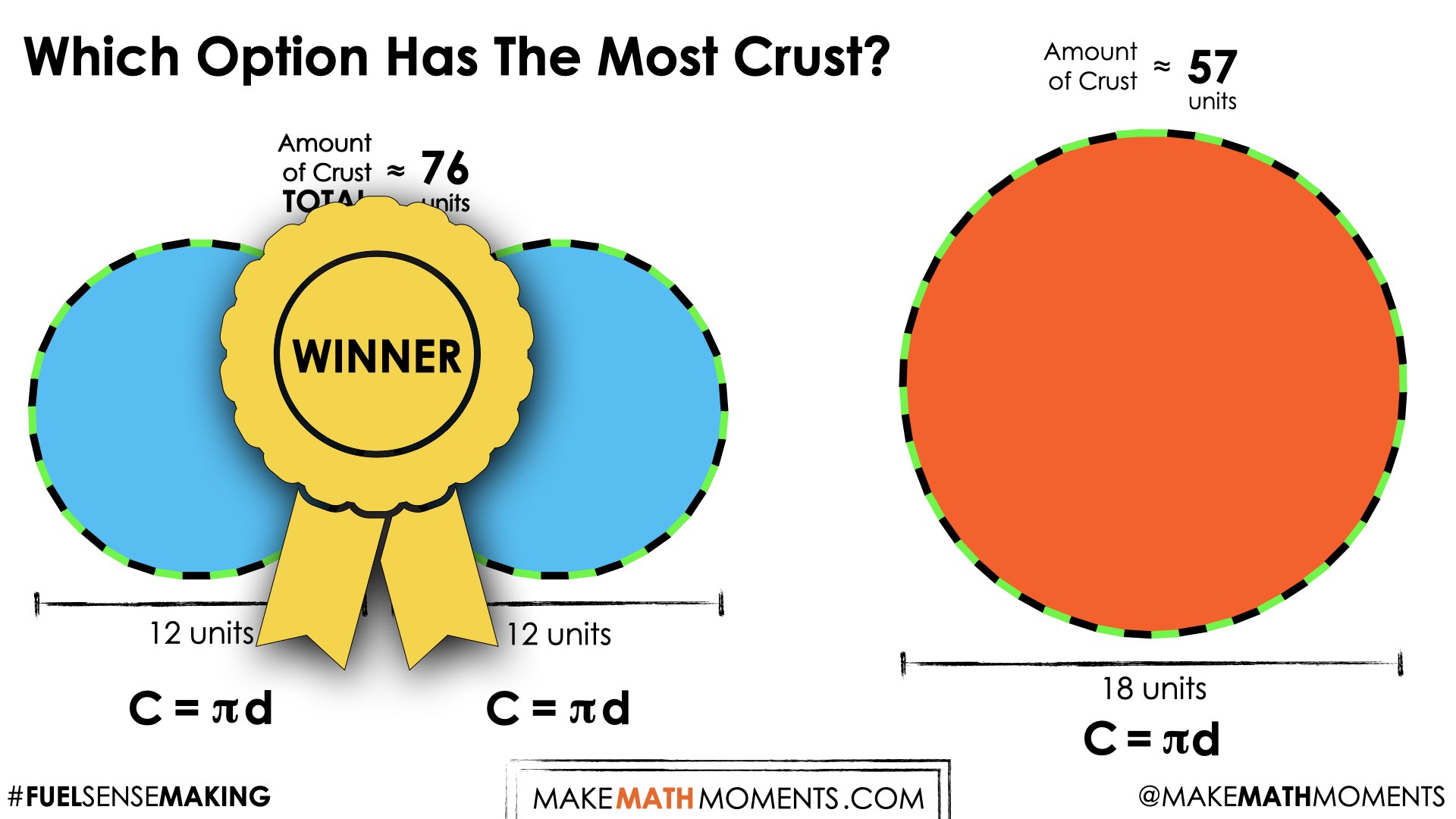
Share the following image revealing the diameter of each medium pizza is 12 units long and the diameter of a large pizza is 18 units long.
Note that we are leveraging non-standard units to make this exploration less about a specific standard unit of measure and more about the relationship between the diameter and the circumference.
Facilitator Note:
Again, this is an excellent opportunity to gain insight as to how students are progressing with their understanding of Pi and circumference of a circle. Use this as an opportunity to document your observations, conversations and student product to help you plan forward as well as to help you when it is time to begin evaluating/reporting.
Give students the necessary time to engage in this exploration noting that if students have not yet developed a deep understanding of the multiplicative relationship between the diameter and circumference of a circle that this activity may take longer than you anticipate. Do not rush students as a lack of understanding here will cause significant challenges later in the lesson as we attempt shifting to finding the area of a circle.
If students are not engaging more deeply with this prompt to come up with a more precise claim, consider asking students not only which has the most crust, but also by how much:
After you’ve updated your estimate, about how much more crust will your selected option give you than the other?
 Allow students to share their thinking including their strategies and mathematical models with the group to update their estimate with a more precise claim.
Allow students to share their thinking including their strategies and mathematical models with the group to update their estimate with a more precise claim.
Reveal
Share the following video revealing the circumference of each pizza and which option has the greatest circumference:
Consider leaving the final frame of the video up on the screen for students to discuss and debrief.
Answer:
Option #1 has the greatest combined circumference of approximately 76 units in length (approximately 38 units of circumference per medium pizza) compared to 57 units of circumference length for the large pizza.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
After celebrating our reasoning and proving from the circumference exploration of each option, extend the context to something like this:
While Tomas and their family enjoys the most crust, we heard that some of you actually throw out your crust! That means that you’re probably not so interested in whether there is more or less crust, but rather which pizza provides the most pizza in total.
So let’s make another estimate.
Turn and talk to your neighbour and come up with an initial estimate for which option you think will give you the most pizza?
Allow students time to discuss and share out their thinking.
Facilitator Notes:
Ensure that students are not searching the internet for a formula or strategy. Explain that you want them to try to make an estimate based only on what they know right now. If some students have already been using a known formula from their prior experiences with area of a circle, encourage them to avoid using the formula itself, but rather to convince us concretely and/or visually. We must ensure that the thinking of other students in the class is not robbed by those who have been either rushed to a formula or algorithm without a conceptual understanding of why that set of procedures actually work. We will allow the formula to emerge and be shared openly when all students have been given the necessary time to investigate and construct understanding.
Consider printing and sharing the first page from the Blackline Master (BLM) PDF handout printable of the pizzas (without the gridlines) so students can make spatial comparisons by placing the medium pizzas overtop of the large pizza, cutting, rearranging, etc.
The pizza templates can be downloaded and printed to give to students to use as a tool for making a more precise estimate here [OPEN | DOWNLOAD]
After students have been given some time to explore and compare using only the pizza cutouts, you might consider sharing one (or more) of the other pages in the template file. By giving some more information such as partial grids, students might be more inclined to try decomposing the circles into more manageable and friendly polygons such as rectangles.
During Moves
While Students Are Productively Struggling…
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Student Approaches
Student Approach #1: Decomposing Medium Pizza Cutouts and Recomposing Over The Large Pizza
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Student Approach #2: Iterating Square Tiles Over Each Pizza Cutout
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Student Approach #3: Decomposing Circles into Friendly Polygons
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Student Approach #4: Using a Known Formula For Area of A Circle
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Next Moves
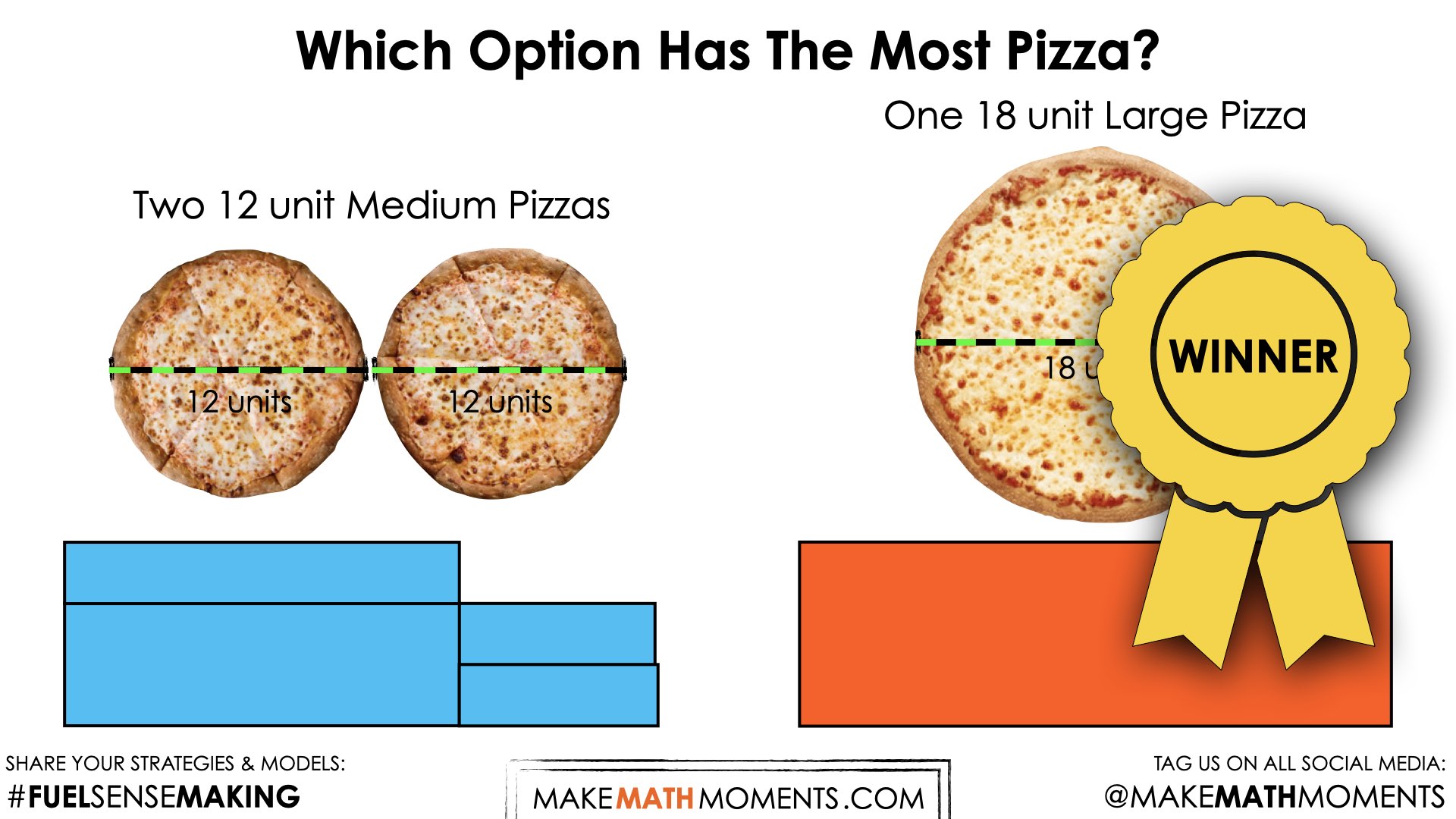
Reveal
Now that students have shared their thinking and have convinced others that the large pizza has a greater area than the two medium pizzas, you can show the following video which will be a nice set up for a more formal consolidation:
Here is a screenshot from the final frame of the reveal video:
Answer:
Option #2 (1 large pizza) has more pizza than Option #1 (2 medium pizzas).
The consolidation will explore the area measures more precisely.
Consolidation
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Reflect and Consolidation Prompts
Students will complete the following consolidation prompts independently.
Consolidation Prompt #1:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Consolidation Prompt #2:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!