CITY CLEANUP
INEQUALITIES
Solve, verify, and graph inequalities.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will solve inequalities involving one operation and represent their solutions on a number line.
Learning goals:
- We will solve inequalities that involve one or two operations and numbers up to 100.
- We will graph our solutions.
Intentionality…
In this task, students will begin exploring inequalities in community service contexts involving whole numbers up to 100. On Day 1, students will explore the idea of greater than and equal to when exploring an inequality that involves multiplication. They will graph the solutions on a number line. Some of the big ideas that may emerge in today’s lesson include:
- In an inequality, the two expressions are not necessarily equal, which can be indicated by the symbols: >, <, ≤ or ≥.
- A number line can show the values that hold for an inequality.
- An open dot on a number line is used when an inequality involves “less than” or “greater than”, and a closed dot is used when it also includes “equal to”.
- Inequalities can be solved as an equation to identify those that hold for the inequality.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following video:

Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on paper.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group.
Some of the noticing and wondering that came up in a class recently included:
- I notice it is a park.
- I notice there is garbage everywhere.
- I notice they are putting the garbage in bags.
- I wonder how much garbage there is.
- I wonder why there is garbage in the park.
- I wonder who is picking up the garbage and why.
At this point, you can answer any notices and wonders you can cross off the list immediately. For example, these are grade 6 students from Westlake Middle School. They have committed to clean up their city through various community service projects. Their first goal is to clean up their local parks. They set a goal to collect at least 100 gallons of garbage.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Since you have already taken some time to set the context for this problem and student curiosity is already sparked, we have them in a perfect spot to help push their thinking further and fuel sense-making.
Share the following silent animation.

You can verbally share the following prompt with students:
Each garbage bag can hold approximately 8 gallons of garbage. If the goal is to collect at least 100 gallons of garbage from the local parks, how many bags should they fill? Represent your solution on a number line.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common misconceptions;
- most common/frequent to least common/frequent representations; or,
- choose another approach to selecting and sequencing student work.
The strategies you might see students use to solve this division scenario include:
- Repeated Addition
- Skip-Counting
- Partial Products
- Partial Quotients
- Keeping the ratio constant
Our goal for this lesson is for students to understand that we can solve an inequality as an equation, and determine all the values that hold true for the inequality. We also want to support students in being able to represent their solutions on a number line.
Most students will likely land on the solution of 12 and \(\frac{1}{2}\) or 13 bags of garbage. If students land on that solution, pose a purposeful question to challenge and extend their thinking.
For example:
What if I told you that 12 and \(\frac{1}{2}\) bags is not the only possible answer? Pay close attention to the question. They want to collect at least 100 gallons of garbage. Could they collect more than 12 and \(\frac{1}{2}\)? How can you show all the possible solutions on a number line?
Student Approaches
Student Approach 1: Skip Counting

I used a table to skip count by 8. For every bag they filled, they added another 8 gallons of garbage. I figured out that they needed at least 12 \(\frac{1}{2}\) bags. The question said they wanted to collect at least 100 gallons. They could collect more. So on the number line, I showed any number of bags more than 12 \(\frac{1}{2}\).
Student Approach 2: Partial Products
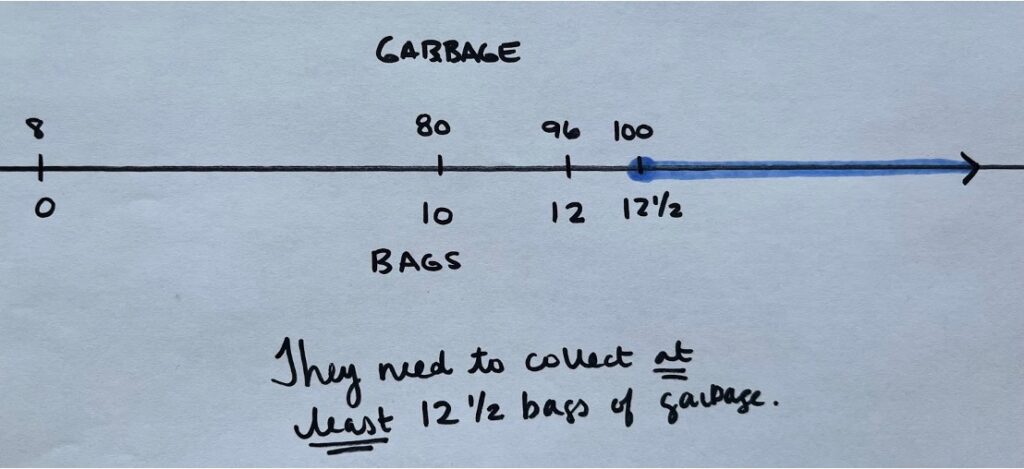
I knew that ten bags of garbage would give them 80 gallons. Another two bags, bringing the total to 12, would be 96 gallons. We need just another half bag to reach the goal. To achieve their goal, they must collect at least 12 and one-half bags of garbage.
Student Approach 3: Simplifying – Keeping the Ratio Constant
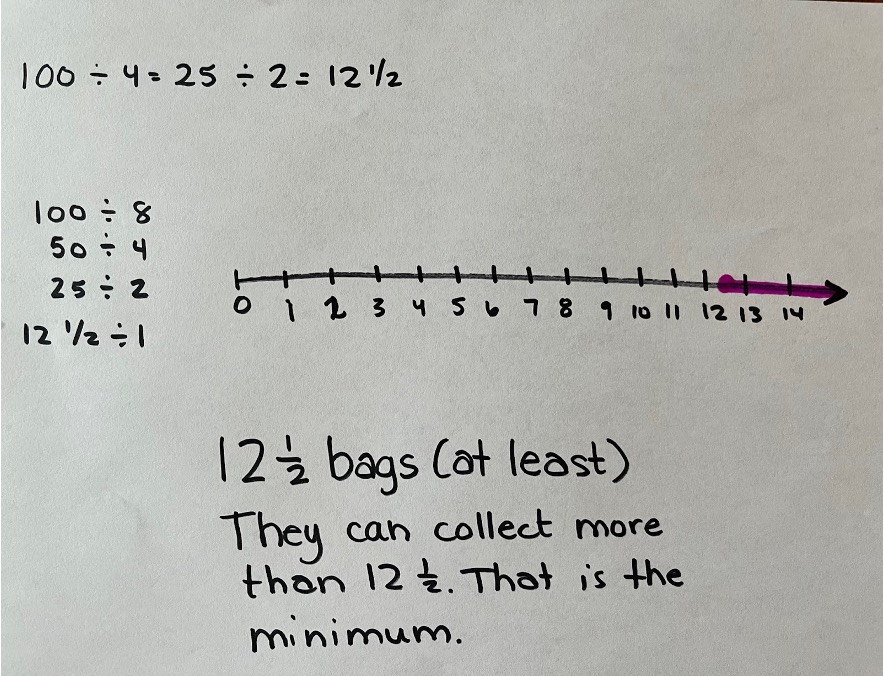
I knew I had to divide the 100 gallons of garbage by the size of the bag, 8 gallons per bag. I found 12 \(\frac{1}{2}\) bags by keeping the ratio constant. I just scaled the division sentence by half each time until I reached 1. They need at least 12 \(\frac{1}{2}\) bags to reach their goal.
Consolidation
This consolidation aims to solidify that inequalities can be solved as equations to reveal which values hold for the inequality.
Support students in understanding how this scenario can be represented symbolically.
Consider asking the following question:
How could we represent this scenario symbolically using one variable and the symbols >, <, ≤ or ≥?
Allow students to discuss with their peers before returning to the whole group.
Leverage student thinking to land on a symbolic representation for this context. For example,
8g ≥ 100
We want to ensure students are familiar with these symbols: >, <, ≤, and ≥.
The total number of garbage bags must be greater than or equal to 12 and \(\frac{1}{2}\) bags.
Share a few student-generated number lines for this inequality. Discuss why this scenario has more than one solution, making it an inequality rather than an equation. The key word in this problem was, at least. Meaning they could collect ANY value greater than or equal to 12 and \(\frac{1}{2}\). A number line is an efficient way to represent all the possible solutions. In this case, we will have an arrow to the right of the number line, indicating that the number of bags exceeding 12 and \(\frac{1}{2}\) is infinite.
Facilitator note:
In this context, the number line will have a solid circle at the value of 12 and \(\frac{1}{2}\) and a solid line extending to the right. The reason for the solid circle is that the solution can include 12 and \(\frac{1}{2}\). The solid line is because any value of bags is possible, including fractional amounts. For example, they could fill 13 and \(\frac{1}{4}\) bags – a possible solution. The data in this context is continuous for both bags and gallons.

Review the learning goals for this unit. Co-construct any additional success criteria that emerged for today’s lesson.
For example:
- We will solve inequalities that involve one or two operations and numbers up to 100.
- I can demonstrate an understanding of >, <, ≤ or ≥.
- I can first solve the inequality as an equation to determine the values that hold for the inequality.
- We will graph our solutions.
- I can show the possible solutions to an inequality on a number line.
- I can use an open dot on a number line when an inequality involves “less than” or “greater than”, and a closed dot is used when it also includes “equal to”.
- I can use a continuous line or points for each value based on whether or not the data is discrete or continuous.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
What is the difference between an equation and an inequality? Explain.
Consolidation Prompt #2:
The grade 6 class is collecting cans for a local food bank. James volunteers to deliver the cans each night on his walk home. The box needs to weigh less than 15 pounds. If each can weighs about 1 ½ pounds, how many cans can James carry in one box?
Solve and graph the solutions on a number line.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students and how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!



