CAN'T GET ENOUGH CEREAL [DAY 3]
VOLUME AND SURFACE AREA OF RECTANGULAR PRISMS
Explore concepts relating to volume and surface area of right prisms.
Intentionality
Math Talk
Visual Math Talk Prompt #1
Visual Math Talk Prompt #2
Visual Math Talk Prompt #3
Visual Math Talk Prompt #4
Purposeful Practice
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 6 Days
Access each lesson from this unit using the navigation links below
Students will reinforce concepts related to the volume and surface area of rectangular prisms and how both volume and surface area relate to multiplication and addition.
Intentionality…
The purpose of Day 3 activities is to reinforce concepts from Days 1 and 2. Students will engage in warm up activities that will encourage them to consider the three dimensional nature of volume in depth, as well as consider how it affects conversions between units within the same measurement system.
Students will also have an opportunity to complete a purposeful practice that will serve to develop a deeper understanding of the following big ideas:
- Volume and surface area are attributes of a three-dimensional space
- The volume of a rectangular prism is related to the edge lengths
- The volume of a rectangular prism can be determined by finding the area of the base and multiplying by the number of layers
- Rectangular prisms can be decomposed into measurable parts
- Area is the amount of surface or space inside a two-dimensional region
- Surface area is additive – area of parts can be combined to find the area of the whole
- Nets of rectangular prisms can be used to think through surface area problems
- The area of a rectangle having fractional side lengths can be found by tiling unit squares of the appropriate unit fraction
What You’ll Need…
A variety of tools for students to use to think through the problems, such as:
- Linking cubes or Omnifix cubes
- Isometric dot paper & colored pencils or markers
- Grid paper
- Whiteboards & markers
Teaching remotely? NCTM’s Isometric Drawing Tool can be used to build and manipulate cube structures
Math Talk
This lesson contains three short, but related Math Talks, which you may wish to conduct on the same day, or spread out over more than one lesson.
Present each of the visual math talk prompts, one at a time.
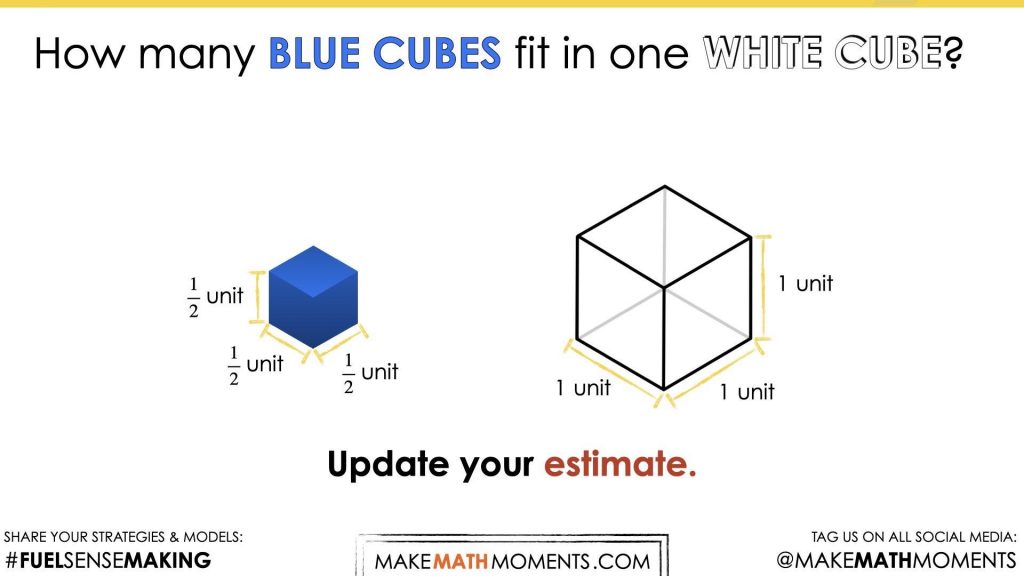
How many small cubes fit in the large cube?
Throughout each prompt, students will be asked to first estimate using their spatial reasoning followed by updating their estimates using a given multiplicative comparison between the dimensions of the small cube compared to the dimensions of the large cube.
The dimensions of the small cube and the large cube for each prompt are listed below:
Small Cube Dimensions: \(\frac{1}{2}\) unit x \(\frac{1}{2}\) unit x \(\frac{1}{2}\) unit
Large Cube Dimensions: 1 unit x 1 unit x 1 unit
Login/Join to access three (3) additional Visual Math Talk Prompts as well as the Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Visual Math Talk Prompt #1
Begin by showing students the following VIsual Math Talk Prompt video and asking them:
What do you notice?
What do you wonder?
Show students the second Visual Math Talk Prompt video
Some possible observations students might share include:
- I notice that there’s a blue cube and a white cube
- I notice that the blue cube is smaller than the white cube
- I wonder how many blue cubes fit into the white cube
Of course, these are just some possible observations and many more ideas may be highlighted by your students.
Continue by asking students to consider the following:
How many blue cubes fit into a white cube?
Make an estimate.
Note that students are being asked to use visual/spatial reasoning first, as they are being asked to consider relative sizes of the cubes before being given dimensions.
Once students have begun to make estimates about the number of blue cubes that will fit into the white cube, you might first reveal the dimensions of the white cube and ask students to estimate the dimensions of the blue cube.
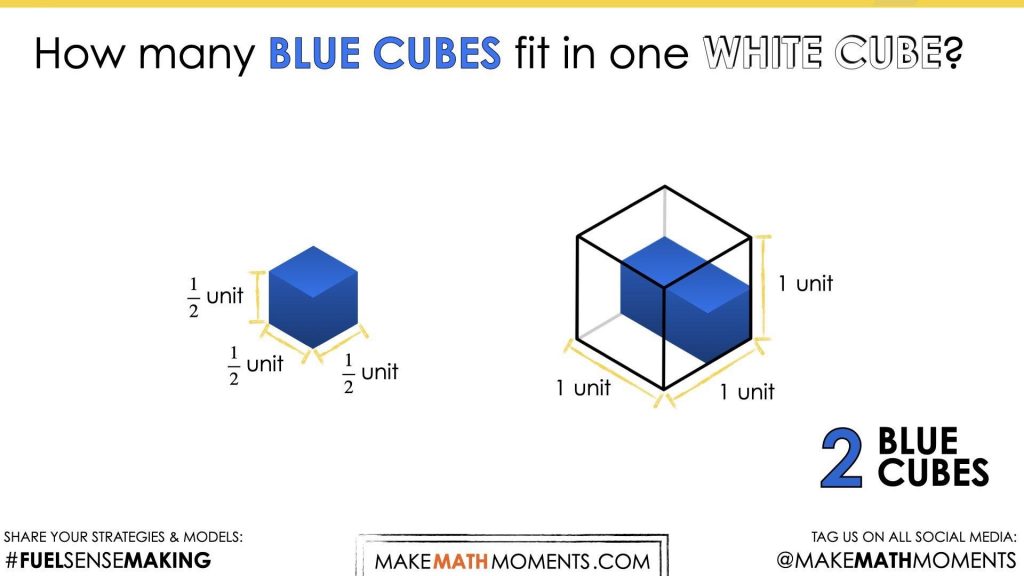
Students may be able to visually reason that each dimension of the white cube fits two of the blue cubes. However, some students may benefit from using wooden cubes or linking cubes to help them think through the problem. Encourage students to share their reasoning and to paraphrase the reasoning of others before revealing the next image:
As students update their estimates, be sure to ask them to reason through how they came up with their refined estimate or why they are sticking with their original estimate.
As you continue to play the visual, students will be able to see the bottom layer filling up first:
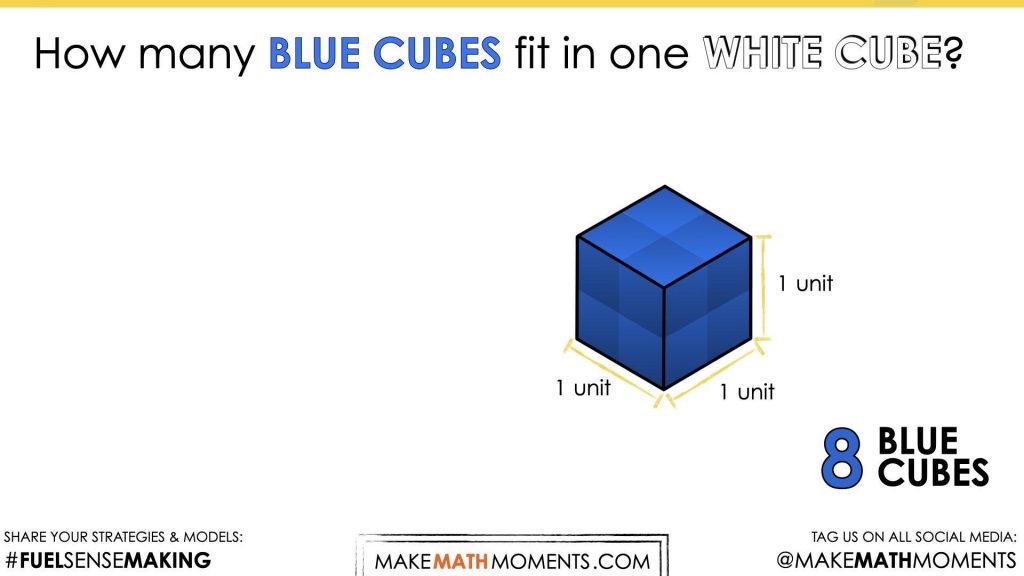
Followed by the top layer to reveal that 8 blue (small) cubes can fit in the white (large) cube.
Consider asking students:
What is the volume of the blue cube?
Students may see that the volume of the blue cube is \(\frac{1}{2}\) x \(\frac{1}{2}\) x \(\frac{1}{2}\) = \(\frac{1}{8}\) while others might initially believe that the volume must be \(\frac{1}{2}\) square-unit.
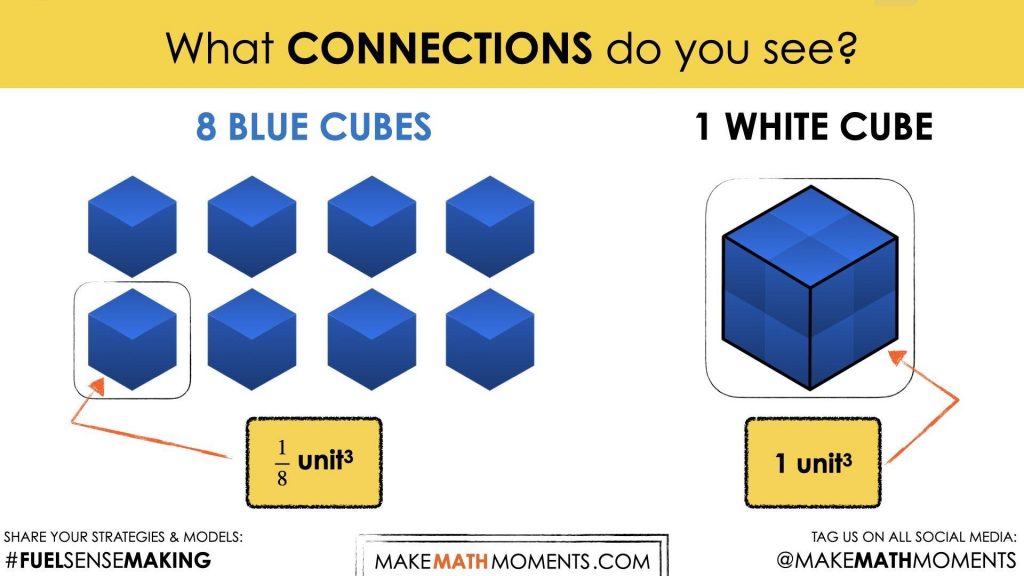
Consider asking students:
What connections do you see?
The goal here is for students to realize that there is a multiplicative relationship between the volume of both cubes; the larger cube is 8 times the volume of the smaller cube and the smaller cube is \(\frac{1}{8}\) the volume of the smaller cube.
Visual Math Talk Prompt #2
Show students the second Visual Math Talk Prompt video:
Ask students to consider the following:
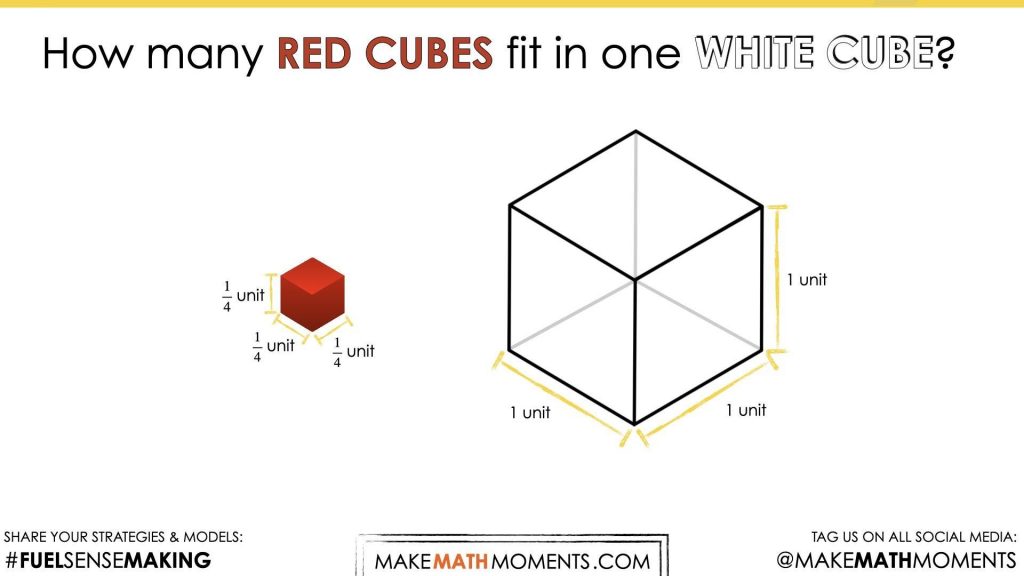
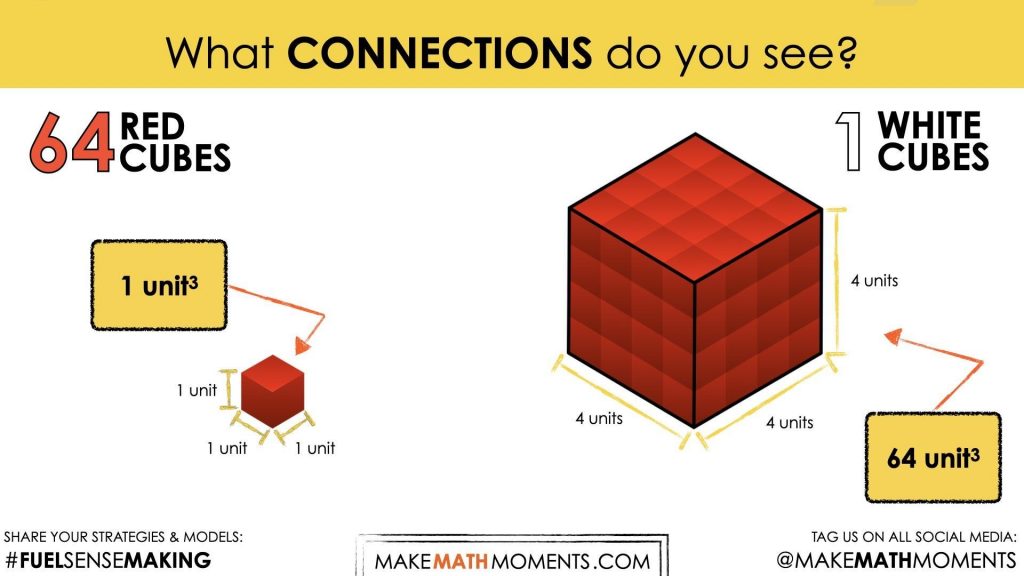
How many red cubes fit into a white cube?
Make an estimate
Again, students may be able to visually reason that each dimension of the white cube fits four of the red cubes. However, some students may benefit from using wooden cubes or linking cubes to help them think through the problem.
You might then reveal that the side lengths of the red cube is 1 fourth of the length of the white cube and allow students to update their estimates.
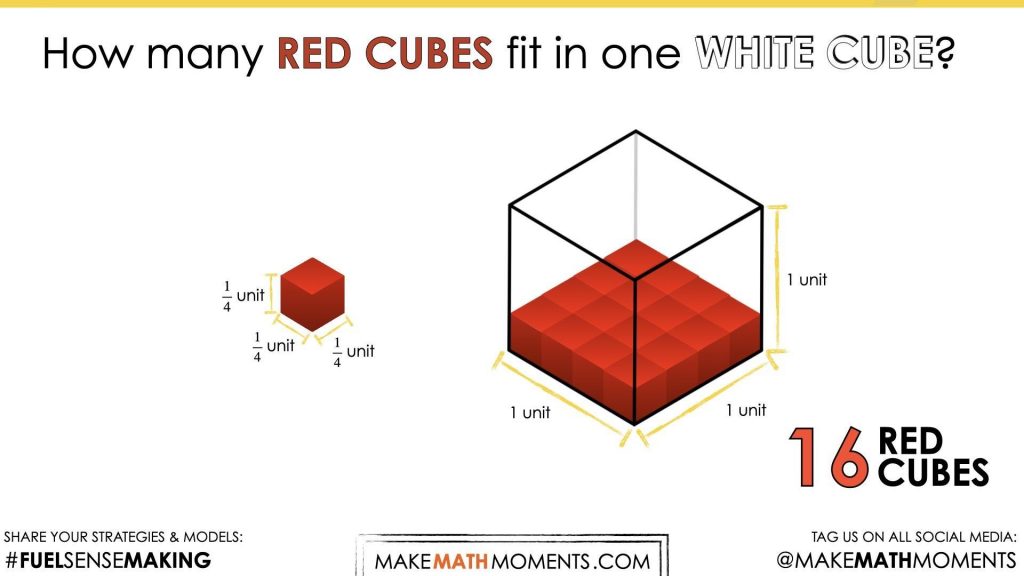
Continue playing the video to reveal how many red cubes it takes to ‘fill’ or ‘cover’ the bottom layer of the white cube and once again ask students to:
Update your estimate.
Throughout the duration of this Visual Math Talk Prompt, be sure to encourage students to share their reasoning and to paraphrase the reasoning of others.
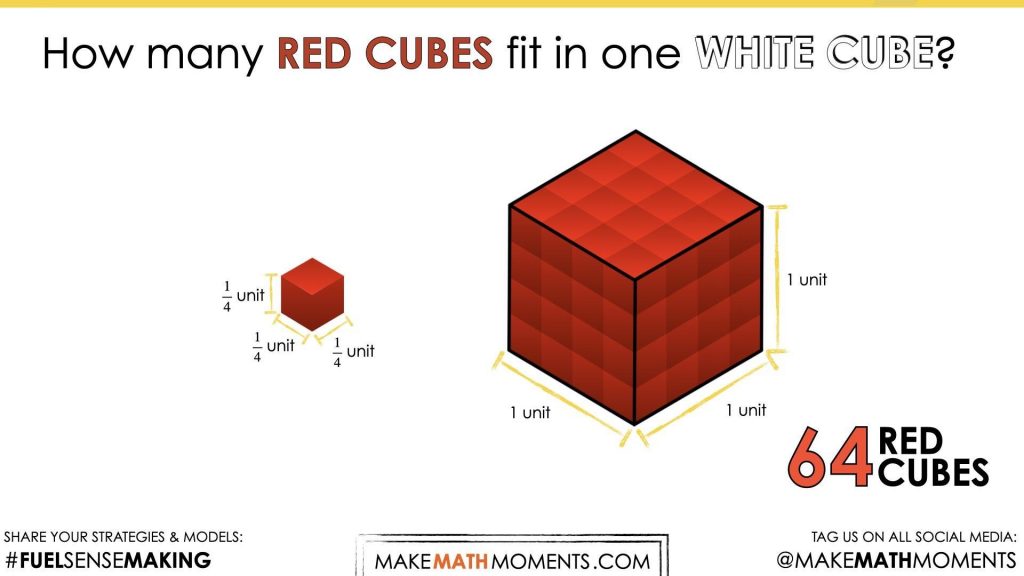
As the silent solution animation continues on, students will see that 64 red cubes fit inside 1 white cube.
Some prompts you might consider include:
What is the volume of the white cube?
What is the volume of the red cube?
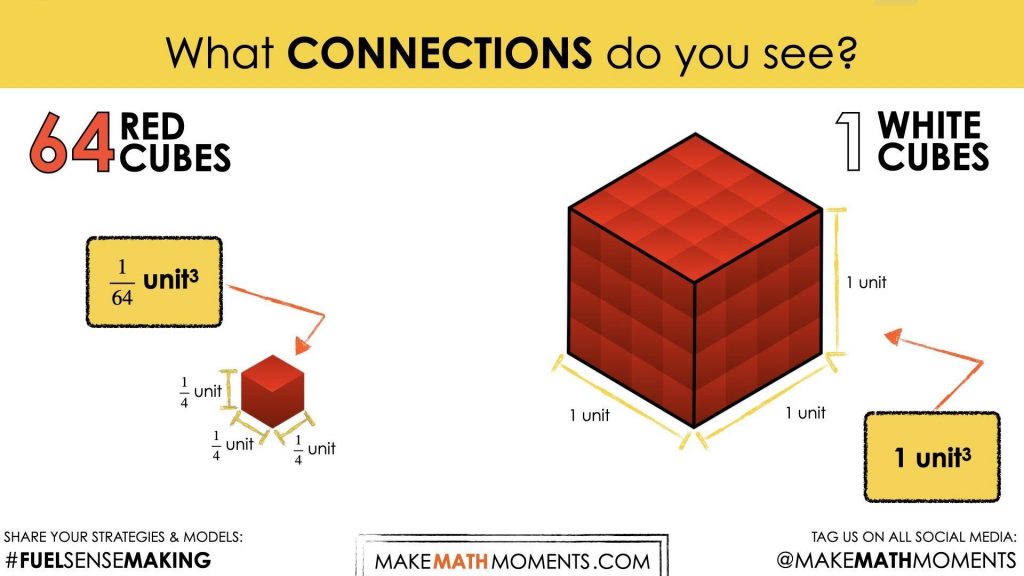
What connections do you see?
Note that some students might say something like:
The volume of the white cube is 64
This is an important facilitator move to notice and name the fact that they are not referencing the unit of measure (1 red cube). Further, we should note that we often default to using the lesser quantity as a unit of measure (in this case, the red cube). You might consider prompting students to identify the volume of the red cube assuming we are using 1 white cube as the unit of measure by asking:
What is the volume of the red cube using 1 white cube as your unit of measure?
In other words:
How many white cubes can fit in a red cube?
Students may come to realize that the volume of the red cube is 1 sixty-fourth of a white cube since 64 red cubes can fit inside a white cube.
Other students might apply their understanding of volume to multiply the dimensions of the red cube of \(\frac{1}{4}\) x \(\frac{1}{4}\) x \(\frac{1}{4}\) = \(\frac{1}{64}\) .
If students do not mention the connection between the product of the dimensions of the red cube (\(\frac{1}{64}\)) and the number of red cubes that fit into the white cube (64) consider bringing it to their attention at this point.
Ensure that you reiterate the reciprocal relationship when we change our perspective utilizing one of the cubes as the unit of measure to the other (i.e.: the 64 and \(\frac{1}{64}\) relationship).
Visual Math Talk Prompt #3
Login/Join to access the full Math Talk, teacher guides, downloadable slide decks and printable handouts for this lesson and all problem based units.
Visual Math Talk Prompt #4
Login/Join to access the full Math Talk, teacher guides, downloadable slide decks and printable handouts for this lesson and all problem based units.
Purposeful Practice
Working With Circles: Circumference
Login/Join to access the Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Questions: Volume & Surface Area of Rectangular Prisms
Question #1:
Login/Join to access the Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #2:
Login/Join to access the Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #3:
Login/Join to access the Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #4:
Login/Join to access the Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #5:
Login/Join to access the Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Resources & Downloads
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!