CAN'T GET ENOUGH CEREAL
VOLUME AND SURFACE AREA OF RECTANGULAR PRISMS
Explore concepts relating to volume and surface area of right prisms.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 6 Days
Access each lesson from this unit using the navigation links below
Students will compare the volume of right rectangular prisms with fractional side lengths as they decide which cereal box has the most cereal.
Intentionality…
In this task, students will compare the volume of rectangular prisms. This task serves to illustrate the relationship between multiplication and volume, as students develop the formula for volume of right rectangular prisms.
Some of the big ideas that will likely emerge in this task include:
- Volume is an attribute of a three-dimensional space.
- Volume can be measured by finding the total number of same-size units of volume required to fill the space without gaps or overlaps.
- The volume of a right rectangular prism is related to the edge lengths.
- The volume of a right rectangular prism can be determined by finding the area of the base and multiplying by the height.
- The volume of a rectangular prism can be determined by multiplying length, width and height.
- The area of a rectangle having fractional side lengths can be found by tiling unit squares of the appropriate unit fraction.
What You’ll Need…
A variety of tools for students to use to think through the problems, such as:
- Linking cubes or Omnifix cubes.
- Isometric dot paper & colored pencils or markers.
- Grid paper.
- Whiteboards & markers.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following image:
Then, ask students:
Which option would you rather?
Share your thinking.
Have students do a Think-Pair-Share routine:
1. Students have individual think time to jot down ideas on paper or whiteboard.
2. Students share their initial ideas with a partner.
3. Students share as a whole group, either their own preference, or a meaningful observation they heard from their partner during the share (while giving credit to their partner). All contributions are acknowledged and recorded on an anchor chart on the board.
Students may have different opinions and perspectives about their preferred option. Possible points that may come up include:
- Option 3 because it looks like it’s less packaging.
- Option 2 because the cereal won’t go stale.
- Option 1 because it looks like it would have the most cereal.
Spending time to acknowledge and address specific thoughts that students shared, whether a notice or a wonder, is crucial to building a culture in your classroom where students know that their voice is being valued and thus encourages them to continue sharing their thoughts and opinions later in this lesson and in future lessons.
Estimation: Prompt
Once students’ initial ideas have been acknowledged and noted, the class can settle on a question to explore:
Which option has the most cereal?
Make an estimate.
Students begin by making an estimate before they are provided with all the information they need to answer the question, thus providing students who may be reluctant to share with a safe entry point.
Be sure not to skip over asking students to make an estimate using only their spatial reasoning skills as this is a very important step in the Curiosity Path. Providing students an opportunity to make an estimate and try to articulate their thinking with their peers provides a very low floor opportunity for them to not only better understand the context, but to also begin nudging them to think about what will be important to make their estimate more precise as we continue through the lesson.
Students should be given an opportunity to share their estimates at this point, but refrain from sharing their rationale just yet in order to give everyone a chance to develop their own thinking.
Have students turn to a partner and generate questions they could ask that would provide them with information they could use to answer the question. Ask students how they would use the information to answer the question.
Prompt:
What information might be helpful to answer this question?
How might you use that information?
Which option has the most cereal?
Update your estimate.
At this point, students may wish to update their estimates. Provide them with time to do so before revealing the next image. A simple prompt might be:
Here are some dimensions. Does this affect your estimate? Would you say your estimate is still reasonable, or will you revise it?
Provide students with time to revise their estimates.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
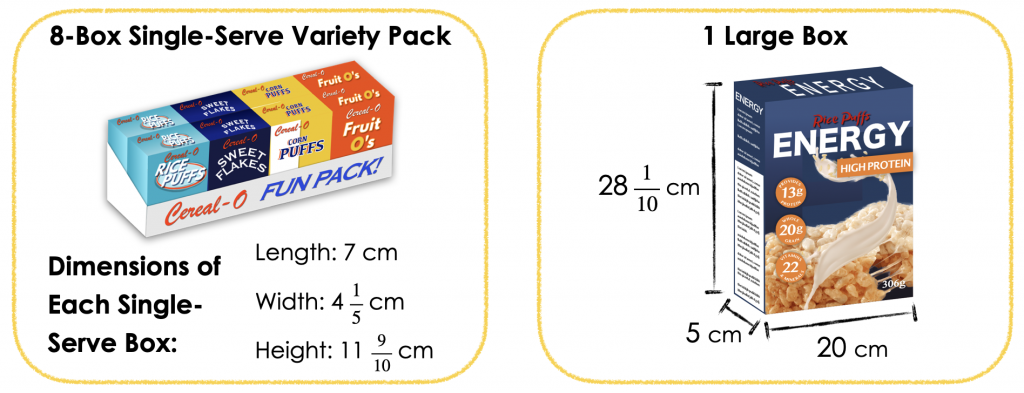
Proceed to reveal the dimensions of the cereal box by showing the following image:
To begin the sense making portion or the lesson, provide students with the following prompt:
The dimensions of each box (along with the number of boxes) are shown in the diagram. Which option would have the most cereal?
Use a mathematical model of your choice to construct a viable argument that clearly shows which option has the most cereal.
Be sure to explicitly state that calculators are not to be used to determine the number of volume of each cereal box. However, do consider making the following tools available to students without explicitly directing students to use them:
- Linking cubes or Omnifix cubes.
- Isometric dot paper & colored pencils or markers.
- Grid paper.
- Whiteboards & markers
Remind students to refrain from shouting out answers, and be sure to emphasize the importance of creating a viable argument – a model that can be used to convince others.
Facilitator’s Note:
There may be students who are familiar with the algorithm who may arrive at a solution rather quickly. This can be an opportunity to reinforce flexibility as you encourage students to solve the problem in a different way.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse.
Listen and observe as students revise their estimates. Are students aware of the connection between the area of the base and the volume of the rectangular prism?
How are students approaching the problem? What strategies and mathematical models are they leveraging? Are they:
- Using additive, scaling or iterative strategies to find the area of the base? (ie: 7 \(\frac{3}{5}\) x 3 = 7 \(\frac{3}{5}\) + 7 \(\frac{3}{5}\) + 7 \(\frac{3}{5}\)).
- Leveraging the distributive property to find the area of the base? (ie: 7 \(\frac{3}{5}\) x 3 = (7 x 3) + (3 x \(\frac{3}{5}\)))
- Using area models to find products?
- Using fraction/decimal equivalencies?
- Using an algorithm?
This is an opportunity to make note of where students are developmentally. Prompt students to explain their thinking and how they plan to use their model/strategy to determine the volume of each cereal box.
Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include, but are not limited to:
- Concrete manipulatives to directly model the rectangular prism
- Mix of multiplicative and additive strategies
- Array or area model for the base with second model for layers
- Use of fraction/decimal equivalencies and an algorithm
Common misconceptions you may consider noting include:
- Confusing volume and surface area
- Using the same dimension twice in calculations
- Errors involving multiplication of fractions
During the consolidation phase, prior to asking students to share their own strategies and reasoning, ask the class if they can discern how the students whose work is being shared were thinking about the problem. A possible prompt might be:
Can you tell how this student/group was thinking about the problem?
This encourages all students to consider alternative viewpoints and begin to seek connections between representations. It helps set up the mindset of “listening to understand” when students share their work.
Have students share their strategies and reasoning for how to represent the volume of each cereal box. Ask them to convince you and their peers that their answer is correct by sharing mathematical models.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
Student Approach #1: Representational Model & Partitioning Strategy
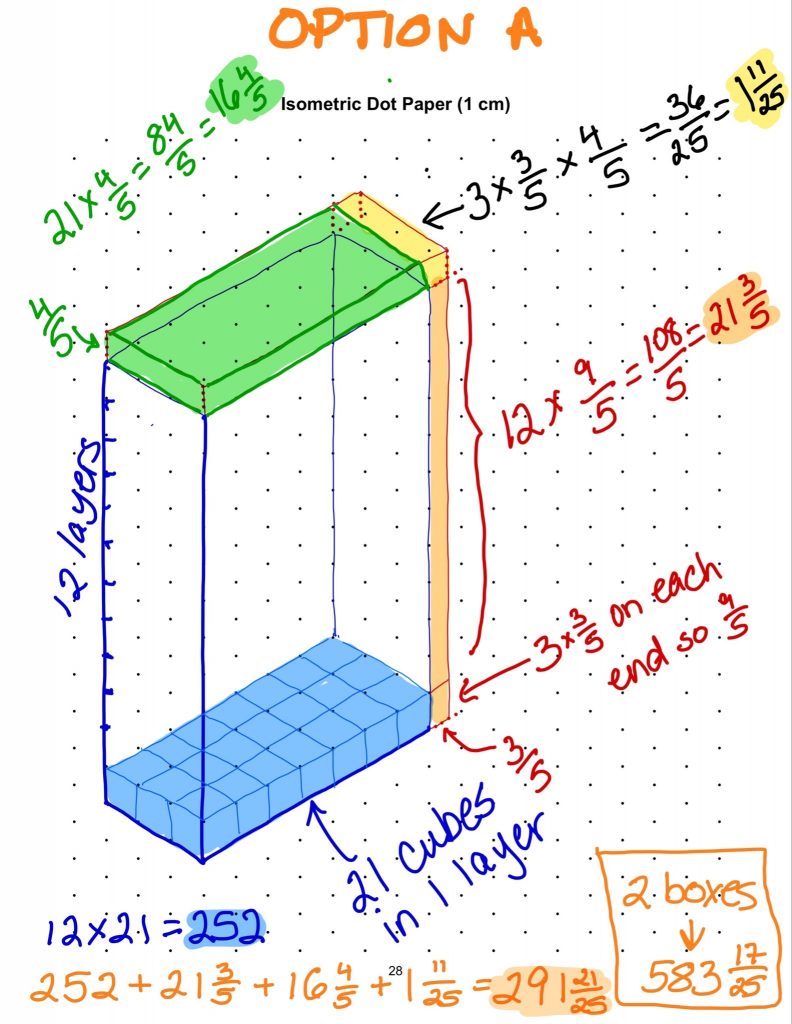
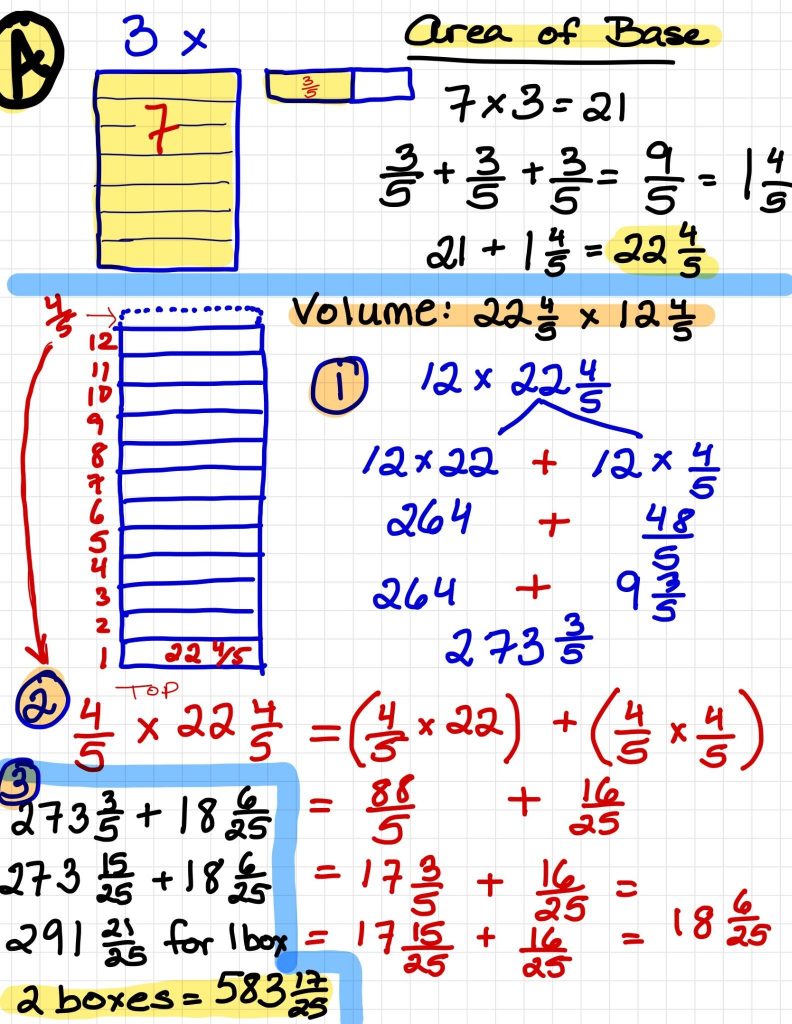
Option A
I drew a picture and then first counted all the whole cubes (blue). There are 21 blue cubes in the bottom layer and there are 12 whole layers, so that’s 252 cubes. Then there’s \(\frac{3}{5}\) of a cube on the end of each row, with 3 rows in each layer, so the bottom layer has 3 x \(\frac{3}{5}\) cubes on the end of it, and that’s . I multiplied by the 12 whole rows and that was 21 \(\frac{3}{5}\) orange cubes. Then I looked at the (green) cubes on top and saw that each of them is 1 x 1 x \(\frac{4}{5}\) and there are 21 of them, so 21 x \(\frac{4}{5}\) = 16 \(\frac{4}{5}\) . The last (yellow) part is 3 cubes long, by \(\frac{3}{5}\) by \(\frac{4}{5}\) which is 1\(\frac{11}{25}\). I added all the parts together and got 291\(\frac{21}{25}\). Since there are two boxes, I doubled it and got 583\(\frac{17}{25}\).
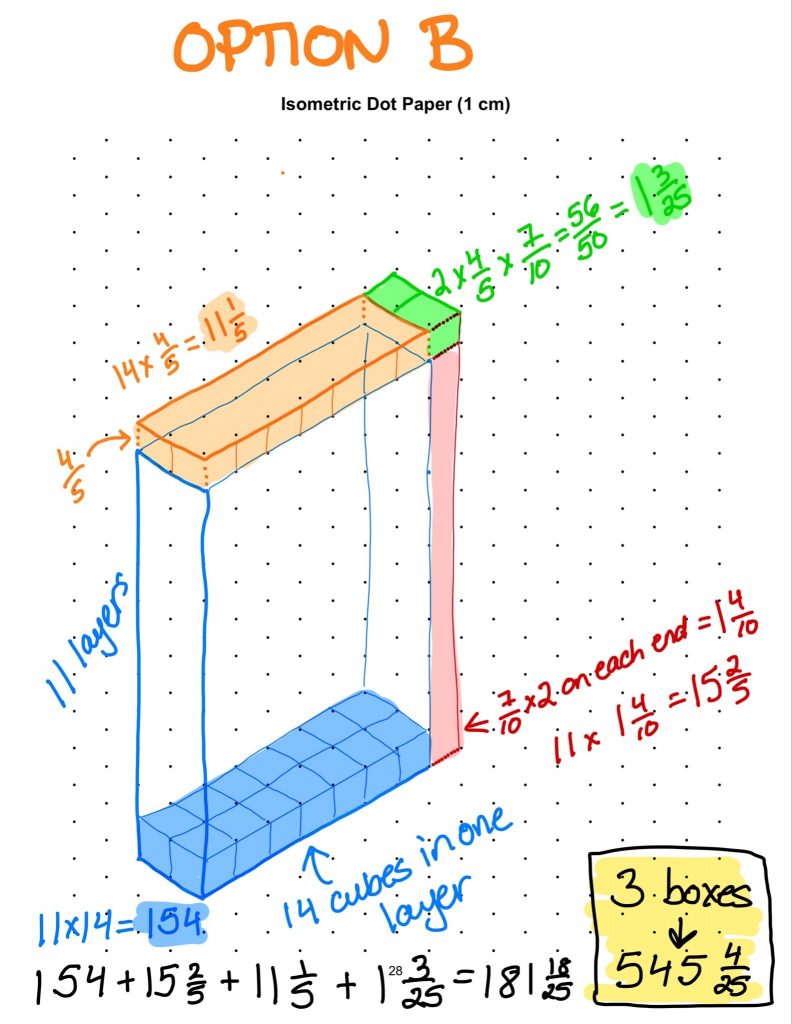
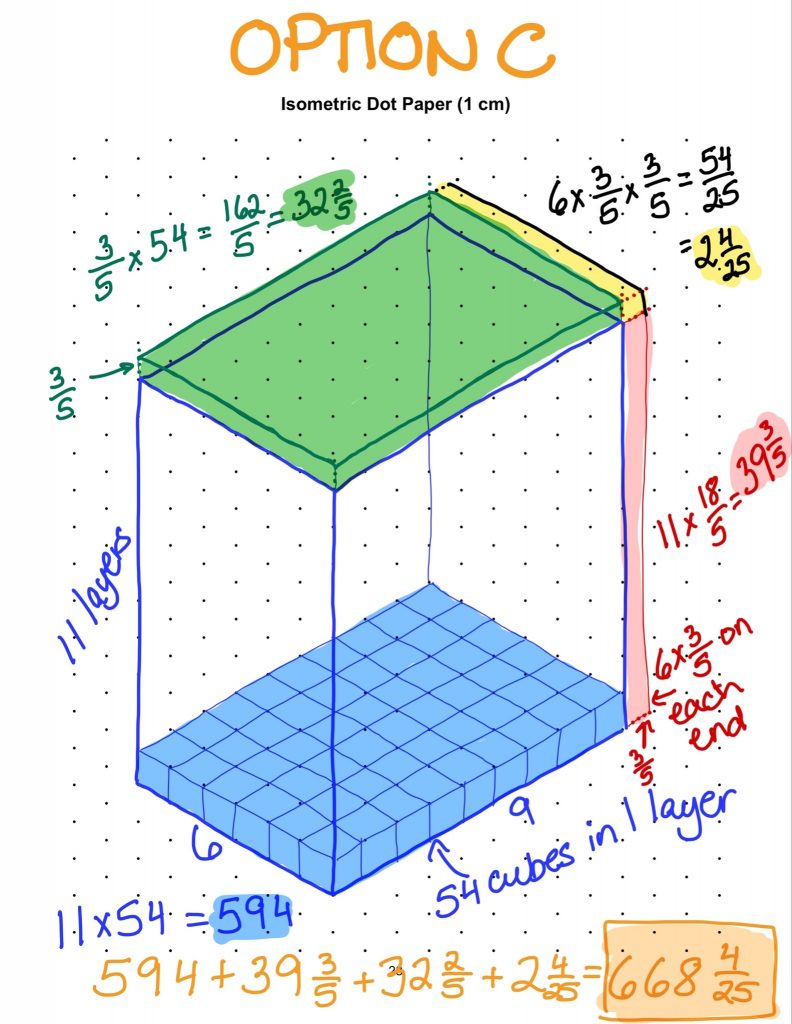
I did the same for Option B and C and found that Option C has the most cereal (668\(\frac{4}{25} units^3\))
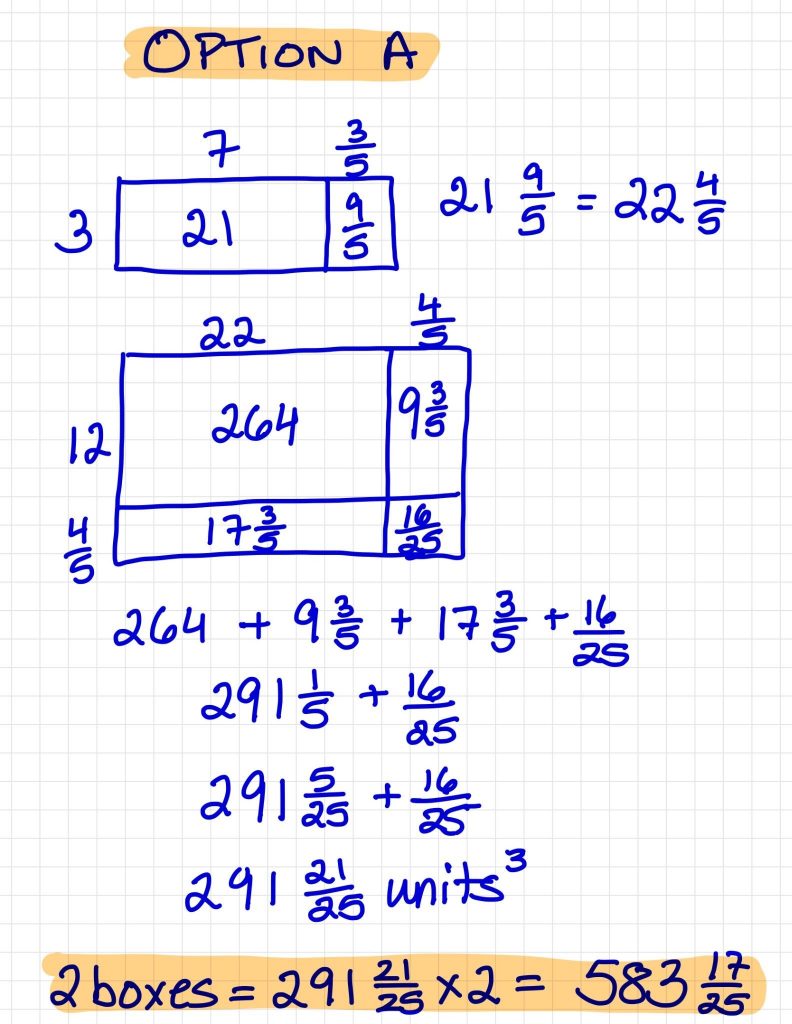
Student Approach #2: Direct Modeling and Area Model
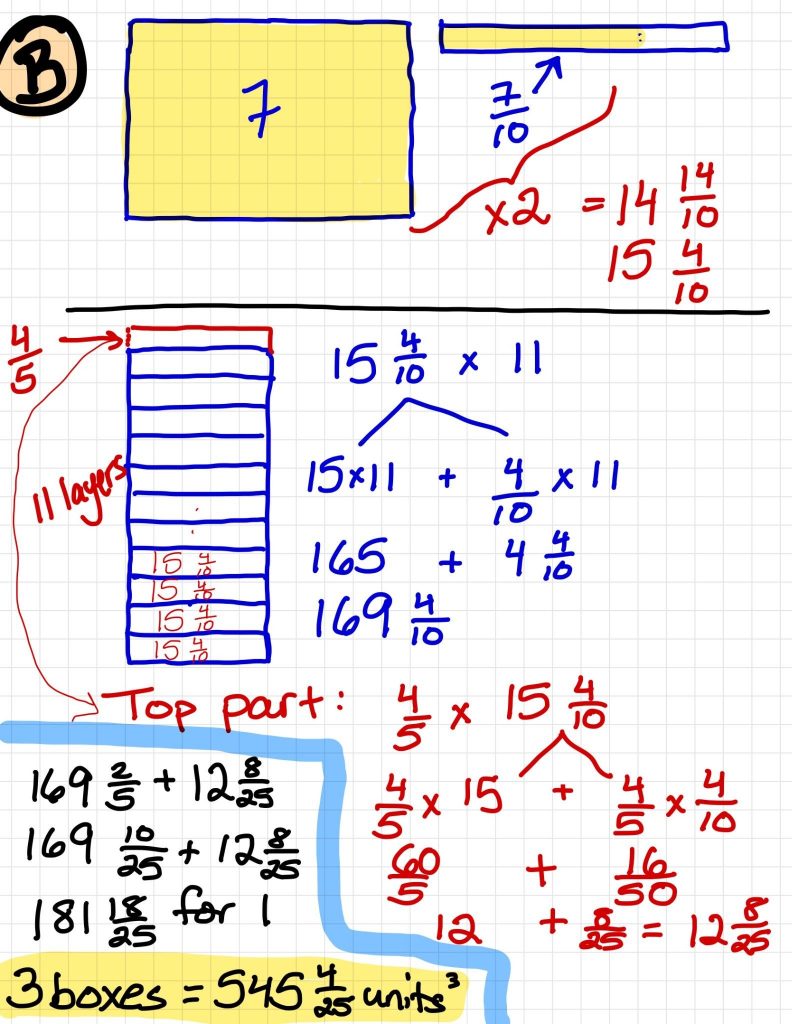
Option A
I know that you first have to find the area of the base, so I used a rectangle to show 7 \(\frac{3}{5}\) x 3 which is 22 \(\frac{4}{5}\). Then you have to multiply that by the height so I used another rectangle and multiplied 22 \(\frac{4}{5}\) by 12 \(\frac{4}{5}\). The answer was 291\(\frac{21}{25}\). Since there are two boxes, I doubled it and got 583\(\frac{17}{25}\). I used the same strategy for Option B and Option C and Option C had the greatest volume.
Student Approach #3: Decomposing Strategies
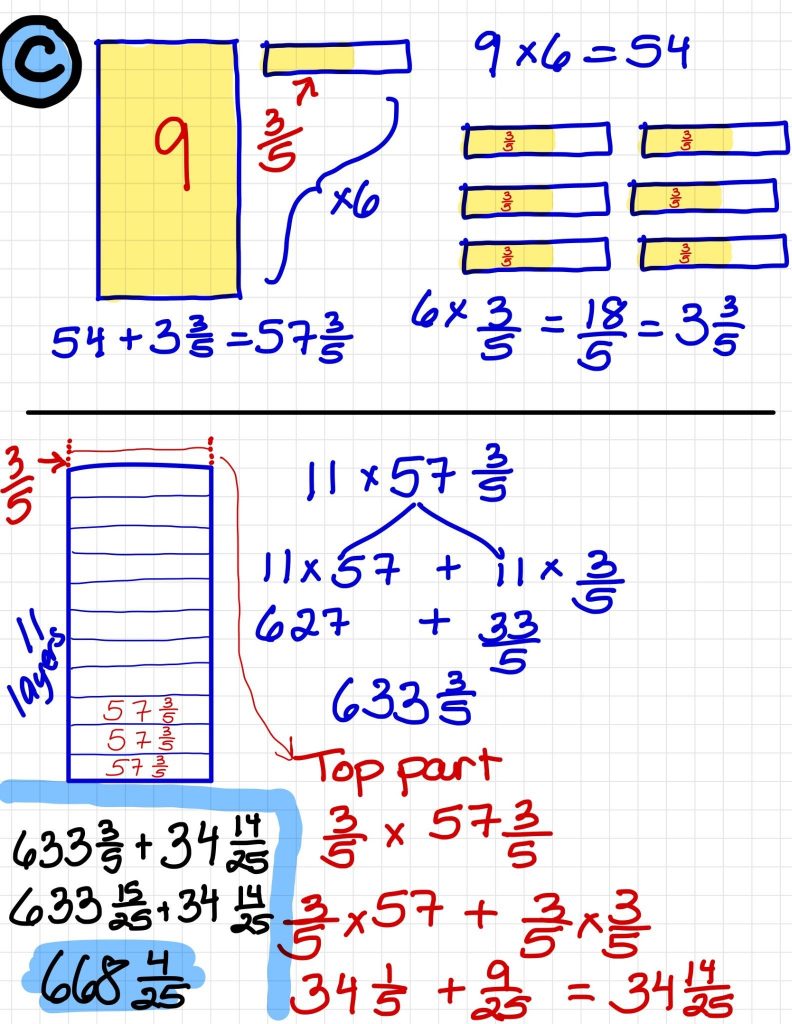
Option A
I know that you first have to find the area of the base, so I did 7 x 3 and 3 x \(\frac{3}{5}\) and put them together. That made 22 \(\frac{4}{5}\) square units for the base. Then I had to multiply that by 12 \(\frac{4}{5}\). First I did 22 \(\frac{4}{5}\) x 12 by breaking apart the 22 and \(\frac{4}{5}\) and got 272 \(\frac{3}{5}\). Then I did \(\frac{4}{5}\) x 22 \(\frac{4}{5}\) by breaking it apart. \(\frac{4}{5}\) x 22 = 16 \(\frac{3}{5}\) and \(\frac{4}{5}\) x \(\frac{4}{5}\) = 17\(\frac{6}{25}\). I put it all together and got 291\(\frac{21}{25}\) for one box, but the deal is 2 boxes so that makes 583\(\frac{17}{25}\).
I did the same for the other 2 boxes and saw that Option C is the one with the most.
Student Approach #4: Fraction/Decimal Equivalencies and Use of an Algorithm
Option A
I know that you \(\frac{3}{5}\) is equivalent to 6/10 and \(\frac{4}{5}\) is equivalent to 8/10. I turned the fractions into decimals and multiplied. The answer was 291.84 for each box, but there are two boxes, so it’s 583.68. I did the same for Option B and C, and saw that Option C has the most volume.
Next Moves
Consolidation
During consolidation, highlight how students went about comparing the options.
As you are discussing student solutions, there is the opportunity to highlight the connection between the volume, the area of the base, and the length of the edges.
Prompt:
What connections do you see between the dimensions (length, width, height) of the cereal box and its volume?
Consider providing students with a word bank that includes the following words:
cubes – volume – layer – dimensions – base – length – width – height – multiply
Conduct a Think-Pair-Share where students first have a moment to consider the question on their own, then turn and talk to a partner, then share as a whole group. Students will likely notice that multiplying the length, width and height of the rectangular prism will yield its volume.
Clearly communicate both orally and in written form the information that was known and unknown in this problem.
Given:
- The dimensions of each of the cereal boxes.
Revealed:
- The volume of each box
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
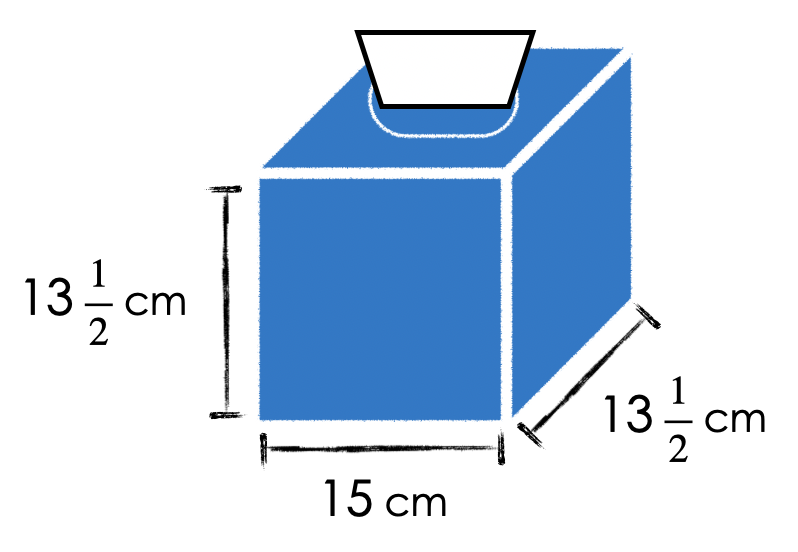
A tissue box has these dimensions:
Length: 15 cm
Width: 13 \(\frac{1}{2}\) cm
Height: 13 \(\frac{1}{2}\) cm
What is the volume of the tissue box?
Consolidation Prompt #2:
Which option offers the most cereal?
Show your thinking.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!