Task Teacher Guide
Be sure to read the teacher guide prior to running the task. When you’re ready to run the task, use the tabs at the top of the page to navigate through the lesson.
In This Purposeful Practice…
Students will extend growing linear patterns. Make near and far predictions and describe the pattern in words.
Intentionality…
The purpose of the Day 4 activities is to reinforce key concepts from Day 3. Students will engage in a math talk using graphical representations of patterns and will have an opportunity to complete independent purposeful practice. The math talk and purposeful practice serve to develop a deeper understanding of the following big ideas.
- Patterns can be extended because they are repetitive by nature.
- Pattern rules are generalizations about a pattern, and they can be described in words.
- One common use of linear patterns is predicting future events.
- A pattern can be extended to make a prediction.
- For far predictions, calculations are required for efficiency.
- In a growing pattern, the values increase.
- In a linear pattern, the values increase at the same rate.
- The rate can be determined by finding the difference between the value of two terms.
- Graphical representations of linear growing patterns appear as straight lines.
- The initial value in a linear pattern is the constant.
- When the initial value is not zero, the relationship between the two variables is not proportional.
Visual Math Talk
String of Related Problems
Present the following graphical representations one at a time using the visual number talk prompt videos below. For each pattern, ask students to describe the pattern rule in words.
Ask students to predict the value of the 8th term and the 13th term. Students are encouraged to justify their thinking. Look for opportunities to build efficiency. For example, once students have determined the rate, and the initial value, rather than counting on or repeated addition, can students leverage this information to perform a calculation?
Visual Number Talk Prompt Video #1
Begin playing the first visual number talk prompt video which will show a graph being created and be prepared to pause when prompted.
The first prompt is:
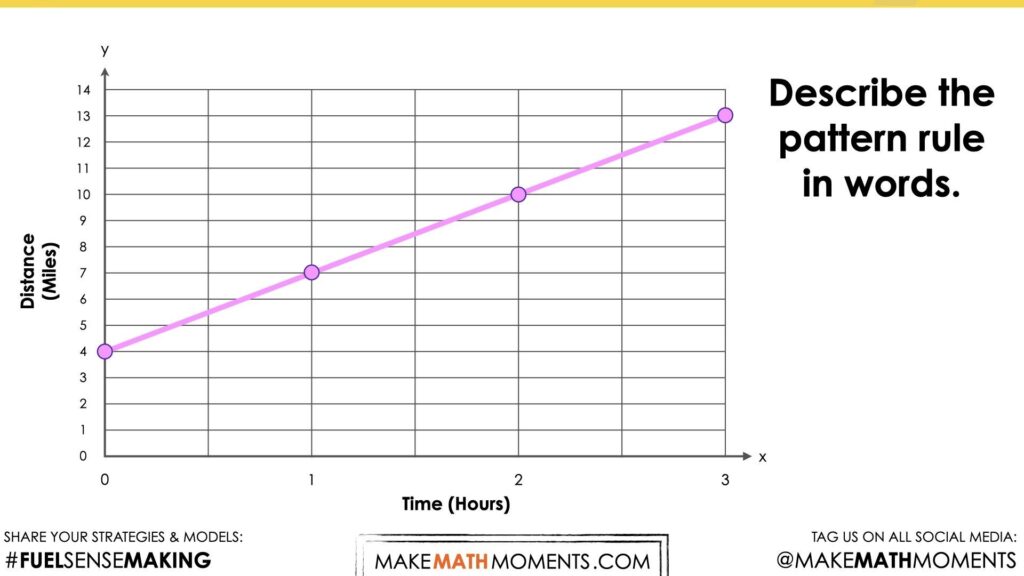
Describe the pattern rule in words.
Be sure to pause the video to give students an opportunity to independently think before turning and talking with a neighbour.
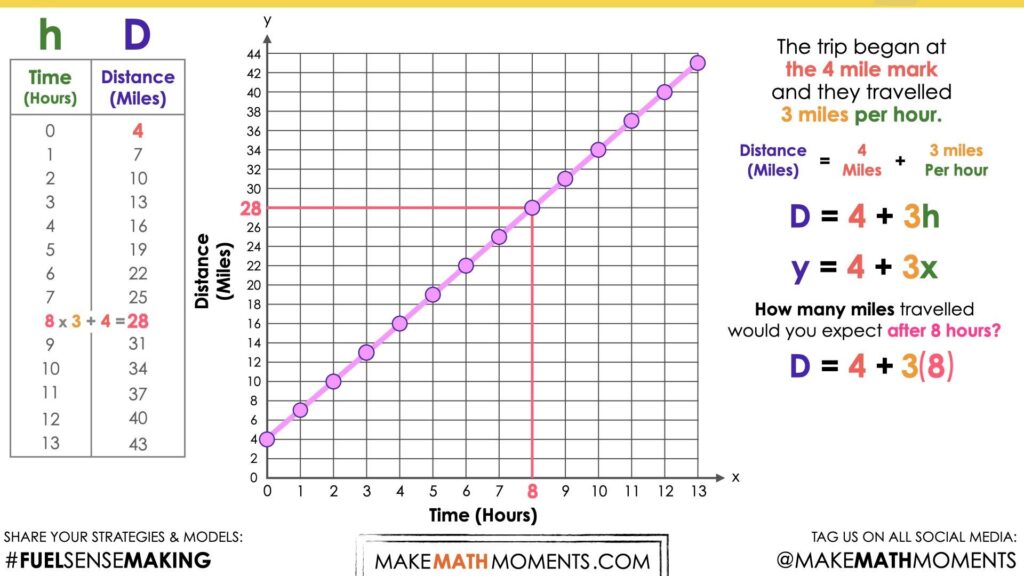
For your reference, the points are (0, 4), (1, 7), (2, 10), (3, 13) which is a linear relationship.
Here are some possibilities for what some students might share with their neighbours and/or out to the whole group:
- The graph is a line.
- It is rising up to the right.
- This graph doesn’t start at 0.
- It is a linear relationship.
- I think we call this an increasing pattern.
- And many other possibilities.
- I wonder if this is another flock of birds migrating?
- The distance is increasing as time goes on.
If students do not elaborate further than this, you might consider prompting students with questions like:
Some of you mentioned that the graph is going “up”. Can you be more descriptive?
Why might the graph start at 4 miles?
How much is it going up by?
Can you be more precise?
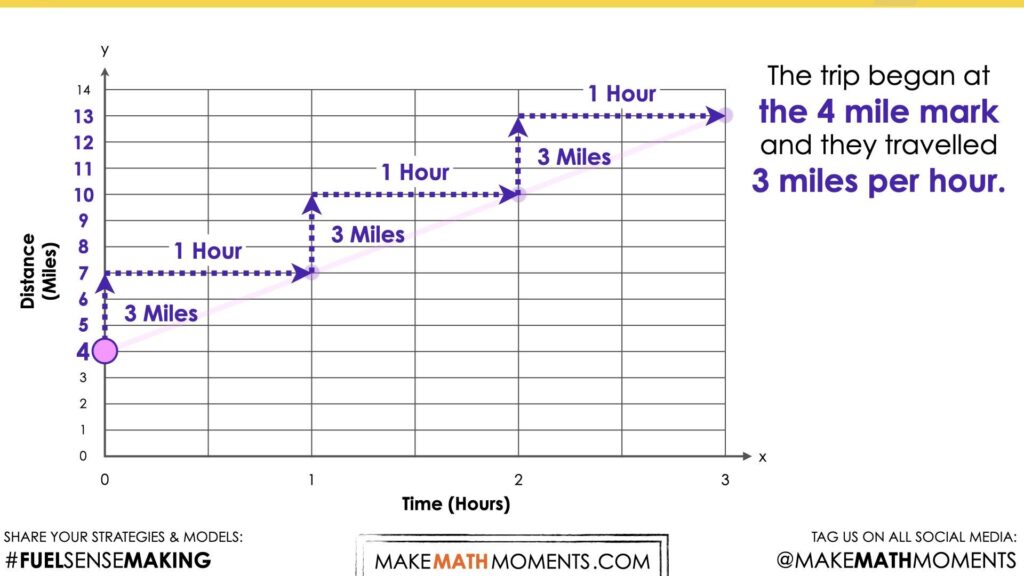
Questions like the above may be able to tease some students to recognize that the distance is increasing by 3 miles for every hour they travel.
Other students might recognize that after 3 miles, they are 13 miles away from wherever they began measuring from.
If you haven’t already, you might want to explain to students that this is another flock of birds and the ornithologist began tracking them when they were 4 miles away from their nesting grounds.
While it may or may not be appropriate to formalize the strategies students are leveraging to help them reveal the rate of change (or slope of the line), it is helpful to note that the strategy students are using here is partitive division of how much the distance increases divided by how much time has passed. When doing this from a graph, many refer to this as determining the rate of change (or slope) as rise over run.
At this point, we can ask students:
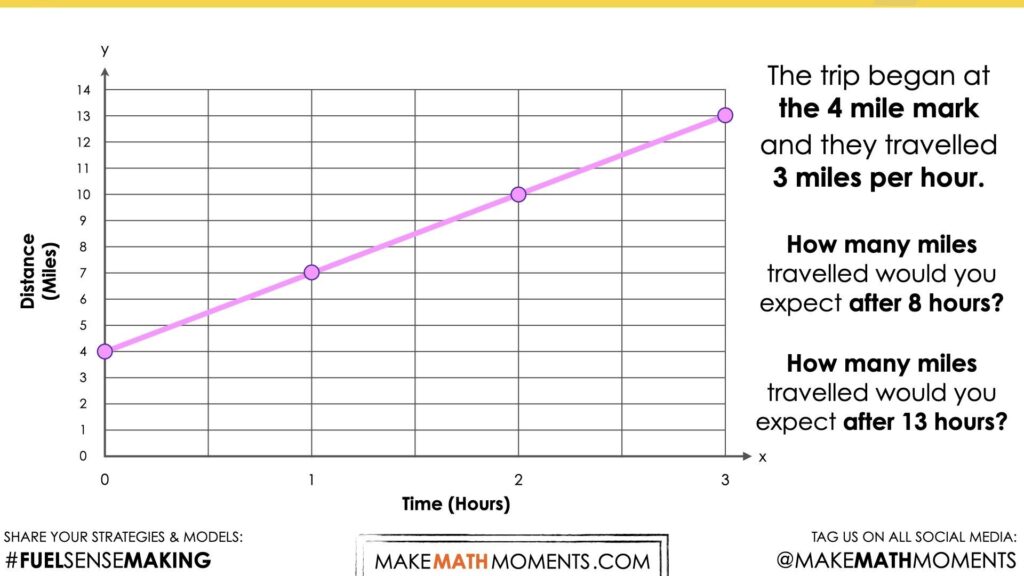
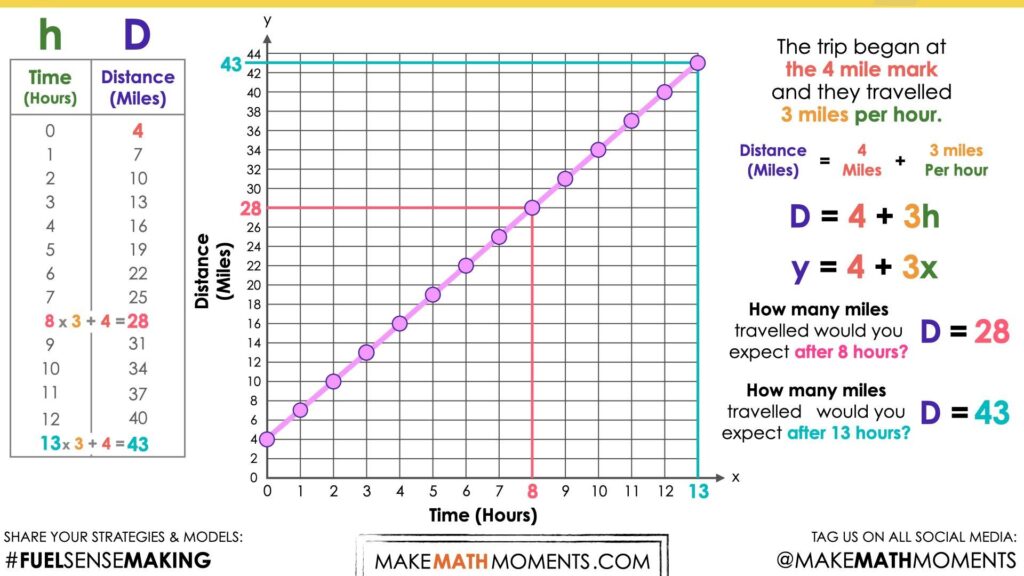
How many miles travelled would you expect after 8 hours?
…. After 13 hours?
Again, being sure to pause so students can think and discuss with a neighbour. Be sure to explain to students that we want their solution to be convincing to others.
Students may begin building a table of values beginning with the first point, (0, 4) known as the initial value and continue recording each point along the linear relationship. Some students may notice that with each passing hour, the distance increases by 3 miles.
While they may not realize it at the time, this increasing pattern of 3 miles for every 1 hour (or ratio) can be leveraged as the rate 3 miles per hour to make determining other values more efficient.
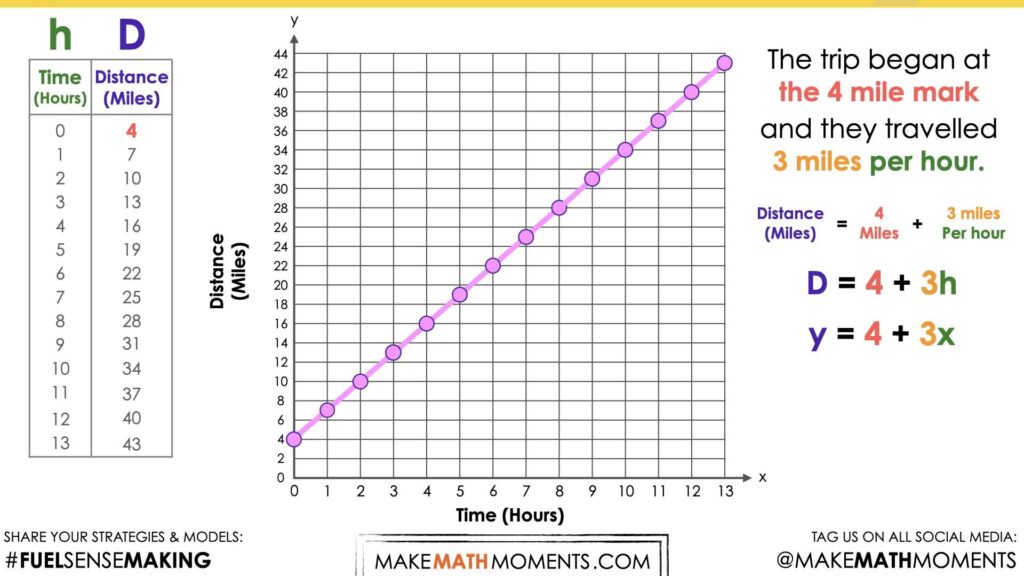
Some students may even recognize that since the graph began at the 4 mile mark and they travelled 3 miles per hour, that we can construct an equation that might look something like this:
Number of Miles = 4 miles + 3 miles per hour
N = 4 + 3h
y = 4 + 3x
By leveraging the equation, we can now substitute 8 hours for the independent variable and simplify to reveal the total distance travelled after 8 hours.
By leveraging the equation, we can do the same for the total distance travelled after 13 hours to confirm the total distance travelled was 43 miles.
While different students may have found the total distance after 8 and 13 hours using different strategies and models, the goal here is to help students extend their thinking to be flexible with multiple representations of linear relationships while ensuring that all students are still able to access the mathematics.
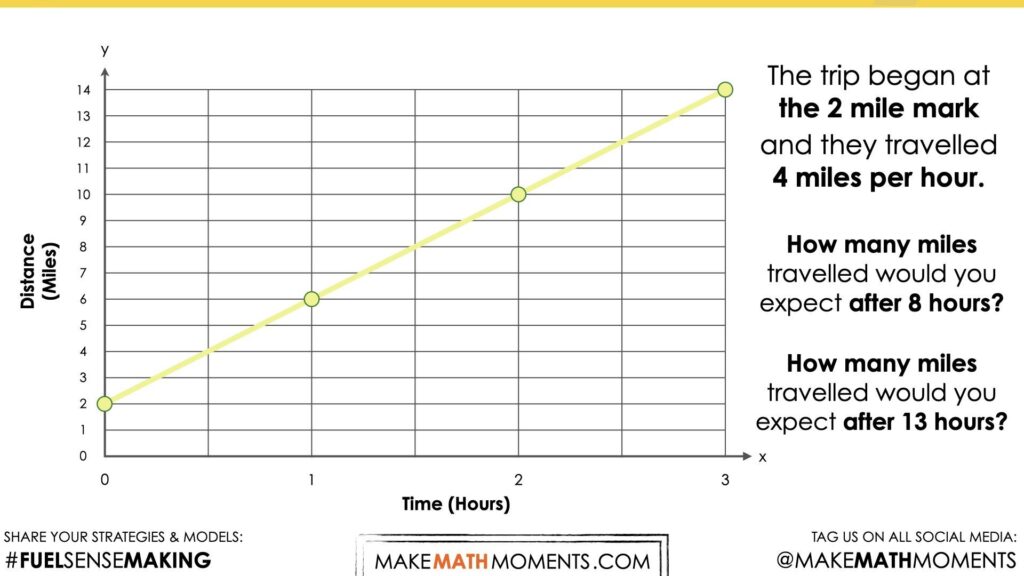
Visual Number Talk Prompt Video #2
Begin playing the second visual number talk prompt video.
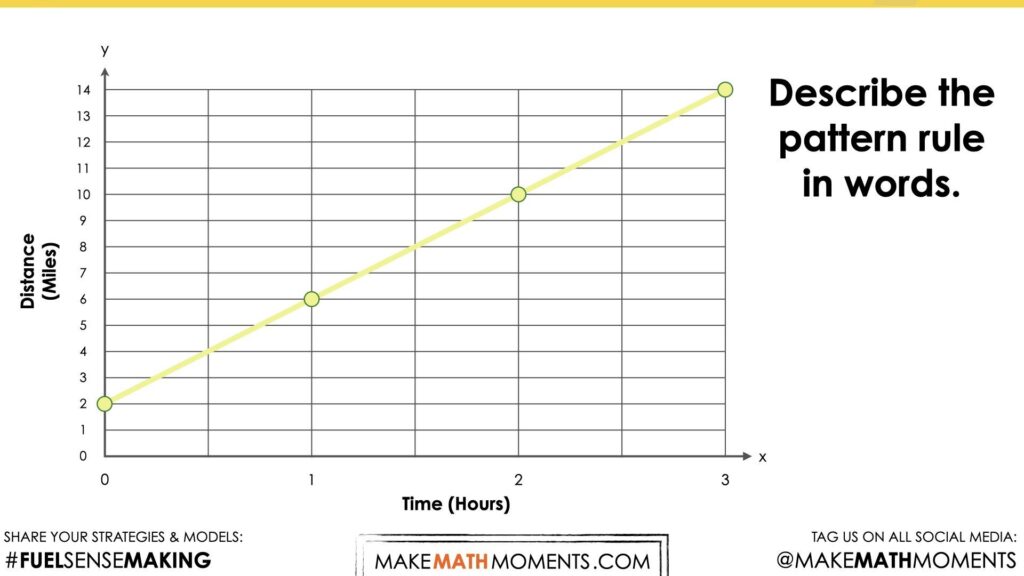
After students watch a graph being created, they will be presented with the following prompt:
Describe the pattern rule in words.
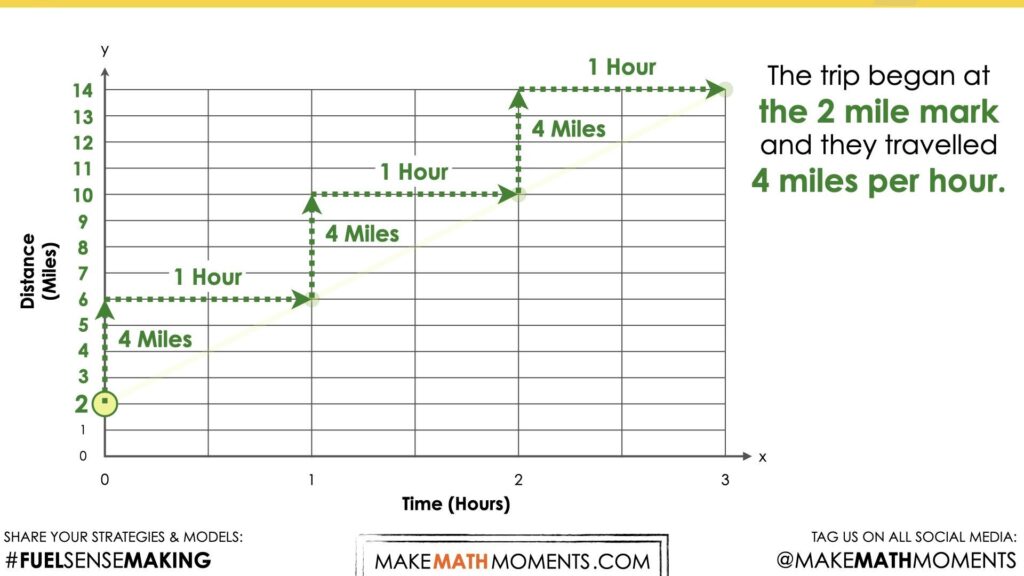
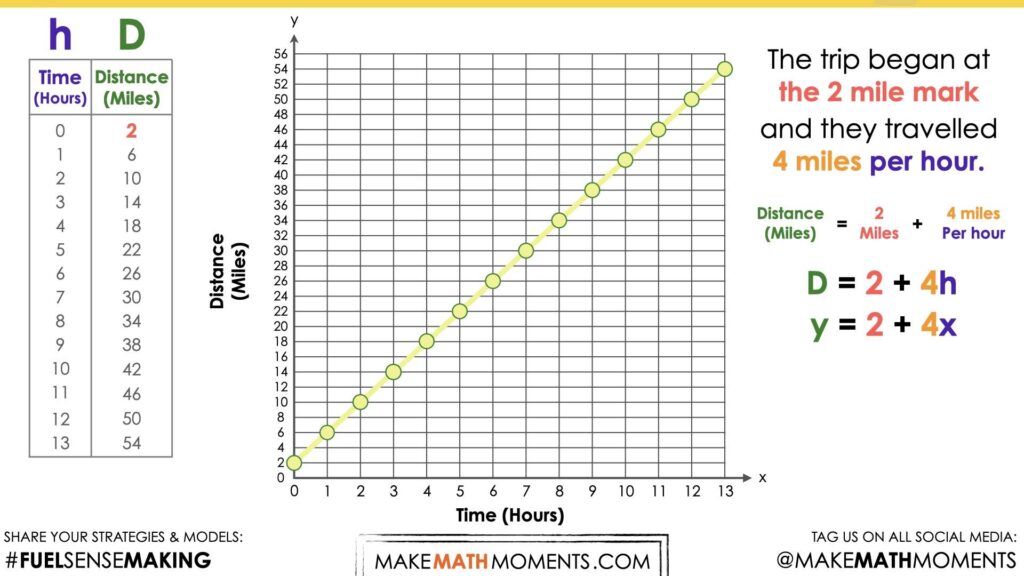
This particular graph has an initial value of 2 miles, (0, 2), and a rate of change (or slope) of 4 miles per hour.
We can now as students to determine:
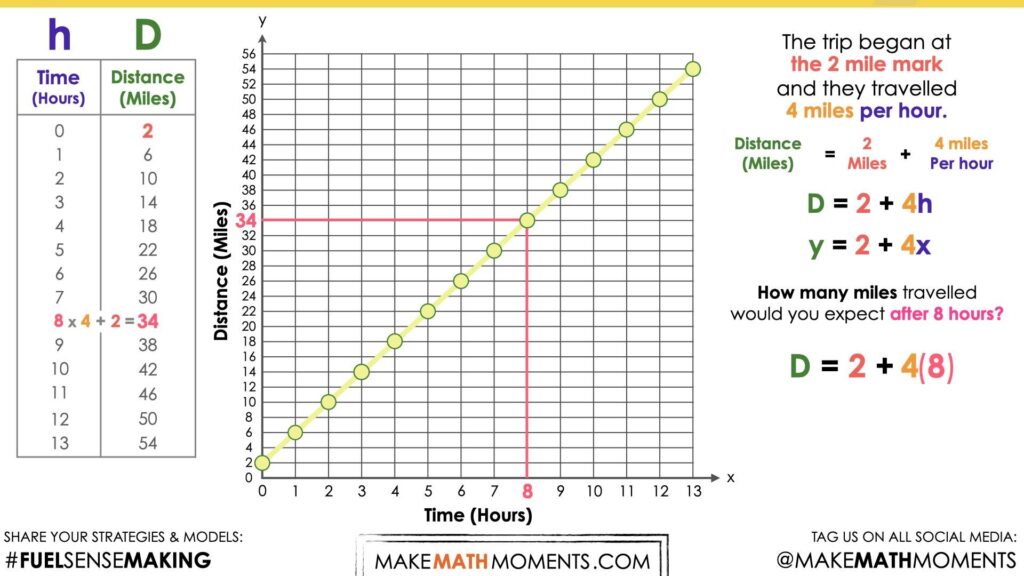
How many miles travelled would you expect after 8 hours?
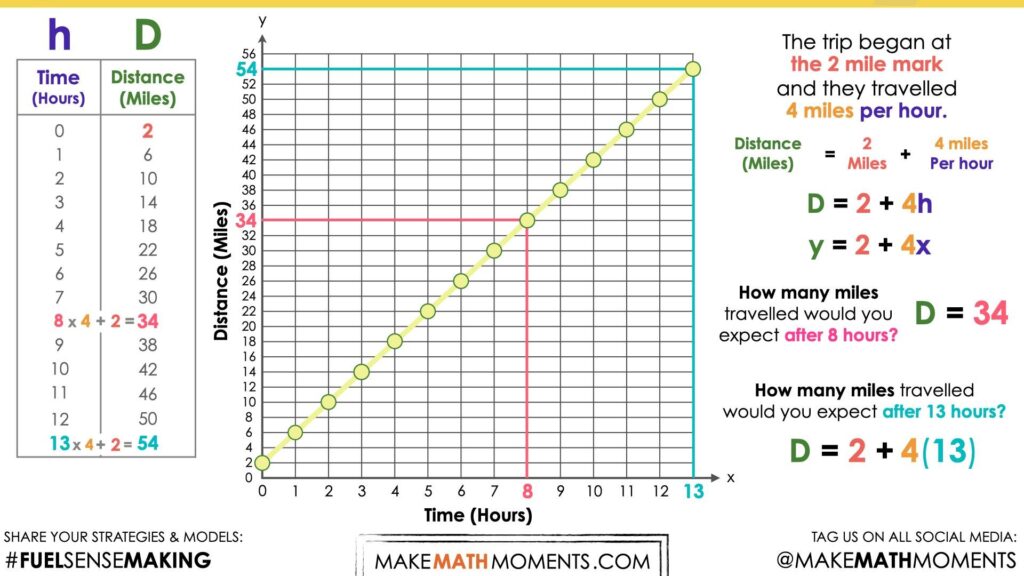
…. After 13 hours?
Leveraging similar strategies as the previous prompt, students can begin to populate a table of values and/or consider crafting an equation using the initial value of 2 miles and the rate of change of 4 miles per hour.
As you can see in the table below, we can quickly determine the total distance travelled after 8 hours and confirm this with our graph and our equation.
The same is true for 13 miles.
Be sure to acknowledge all student approaches and watch for students resorting to additive thinking (i.e.: adding 4 miles each hour in the table) vs. multiplicative thinking (i.e.: determining 8 groups of 4 miles and then adding the initial value of 2) and be sure to reference this during the consolidation.
Visual Number Talk Prompt Video #3
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Visual Number Talk Prompt Video #4
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Purposeful Practice
While Students Are Practicing…
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Questions: Growing Linear Patterns
Question #1:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #2:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #3:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #4:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #5:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Download Editable/Printable Handout
Become a member to access purposeful practice to display via your projector/TV, download the PDF to upload to your LMS and/or print for students to have a physical copy
Resources and Downloads
Lesson Tip Sheet

Download the lesson plan in PDF format so you can keep it handy and share with colleagues.
Videos & Images
 Download the videos, images, and related media files to your computer to avoid streaming.
Download the videos, images, and related media files to your computer to avoid streaming.
Keynote Slides
 Download in Apple Keynote format to avoid streaming video and run the lesson smoothly.
Download in Apple Keynote format to avoid streaming video and run the lesson smoothly.
PowerPoint Slides
 Download in Microsoft PowerPoint format to avoid streaming video and run the lesson smoothly.
Download in Microsoft PowerPoint format to avoid streaming video and run the lesson smoothly.
Printable Handout

Download/Edit the handout so you can keep it handy and share with colleagues.
Explore The Entire Unit of Study
This Make Math Moments Task was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, and extensions to elicit and emerge mathematical models and strategies.
Click the links at the top of this task to head to the other related lessons created for this unit of study.
Visual Math Talk Prompt #1
Visual Math Talk Prompt #2
Visual Math Talk Prompt #3
Visual Math Talk Prompt #4
Question #1
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #2
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #3
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #4
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #5
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Download Editable/Printable Handout
Become a member to access purposeful practice to display via your projector/TV, download the PDF to upload to your LMS and/or print for students to have a physical copy