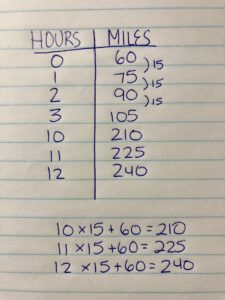BIRD MIGRATION
GROWING LINEAR PATTERNS
Explore growing linear patterns by describing the pattern rule in words, extending the pattern and using the pattern to make a predictions.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview
Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will analyze the migration of a flock of Canadian Geese from Northern Michigan to Southern Michigan in the fall.
Intentionality…
In this task, students will analyze and make predictions about the migration pattern of a flock of Canadian geese. They will predict how long it took for the ornithologist to document 240 miles of flight. Some of the big ideas that may emerge in this unit include:
- Patterns can be extended because they are repetitive by nature.
- Pattern rules are generalizations about a pattern, and they can be described in words.
- One common use of linear patterns is predicting future events.
- A pattern can be extended to make a prediction.
- For far predictions, calculations are required for efficiency.
- In a growing pattern, the values increase.
- In a linear pattern, the values increase at the same rate.
- The rate can be determined by finding the difference between the value of two terms.
- Graphical representations of linear growing patterns appear as straight lines.
- The initial value in a linear pattern is the constant.
- When the initial value is not zero, the relationship between the two variables is not proportional.
Spark Curiosity
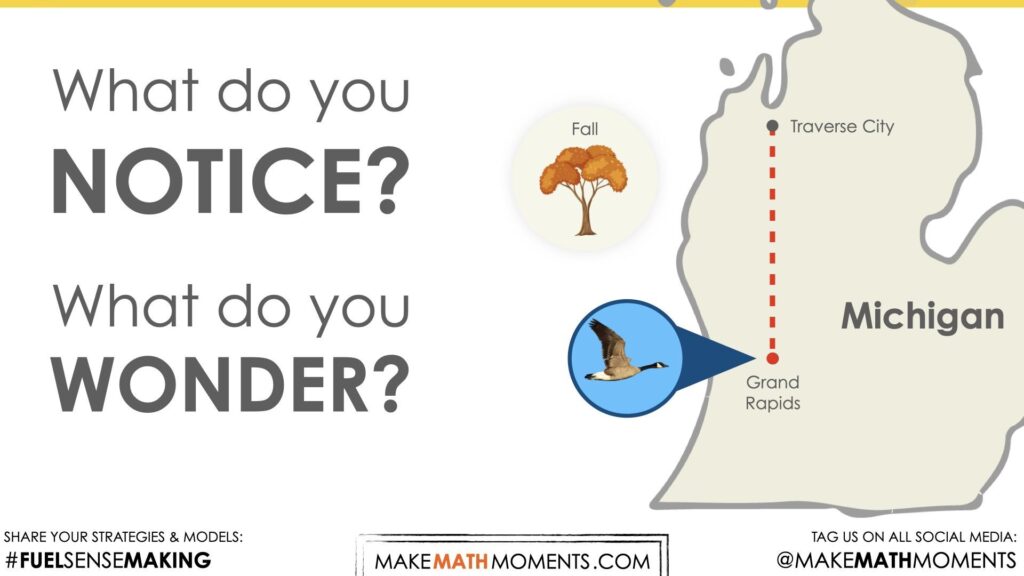
What Do You Notice? What Do You Wonder?
Show students the following video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Replaying the video can be helpful here and consider asking students what they are going to be looking for.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group. Be sure to write down these noticings and wonderings on the blackboard/whiteboard, chart paper, or some other means to ensure students know that their voice is acknowledged and appreciated.
Some of the noticing and wondering that may come up includes:
- I notice it says Michigan.
- I notice an arrow.
- I notice it is moving between two points.
- I wonder if someone is driving.
- I wonder how long it took.
- I wonder how far it is.
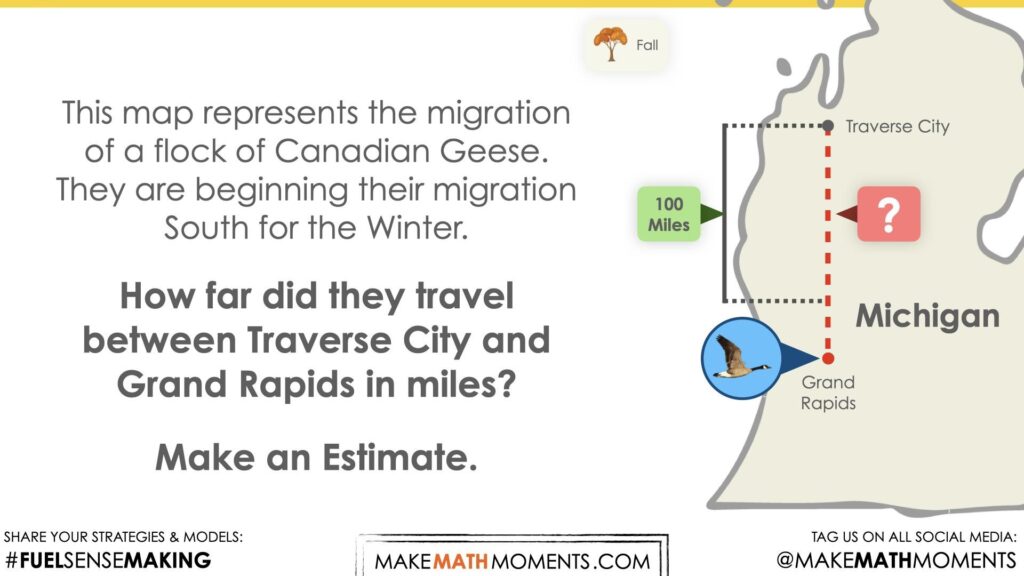
Estimate: Prompt
After we have heard students and demonstrated that we value their voice, we can land on the first question we will challenge them with
This map represents the migration of a flock of Canadian Geese. They are beginning their migration South for the Winter. How far did they travel between Traverse City and Grand Rapids in miles?
Share the following video extending the context a bit further. This time, students will have access to a scale.
We can now ask students to make an estimate (not a guess) as we want them to be as strategic as they can possibly be. This will force them to determine a distance in miles that would be reasonable. Students will likely leverage spatial reasoning. Look for opportunities to use fractional language. For example, the distance between the two points is 1 and \(\frac{1}{2}\) times as big as the scale. The scale is two-thirds the size of the distance travelled.
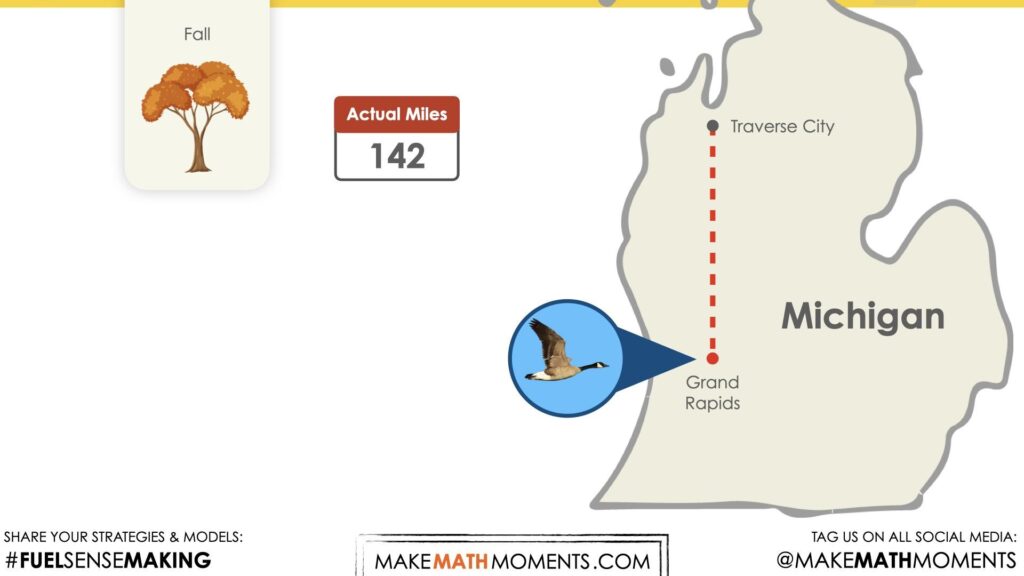
Estimation: Reveal
Share the actual distance between the two points on the map with the following video:
You might consider instead sharing the final frame of the estimate reveal video:
Celebrate student estimates that were very close to the actual distance travelled using a routine of your choice as we head into the sense making portion of this lesson.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Now that student curiosity has been sparked through the use of our Notice and Wonder prompt followed by the opportas 150 miles and 30 milesunity to make an estimate, we will continue to develop the context of this problem and provide a struggle prompt.
Consider sharing the following silent animation struggle prompt video and consider leveraging a variation of the script below to assist:
Canada geese that migrate do so twice a year. In September or October, Canada geese fly south to avoid the cold. They’ll stay there all winter. Geese migrate north in April, May or Early June. Migration flights usually begin at dusk, although you could see migrating geese flying in their distinctive “V” formation at any time of hour.
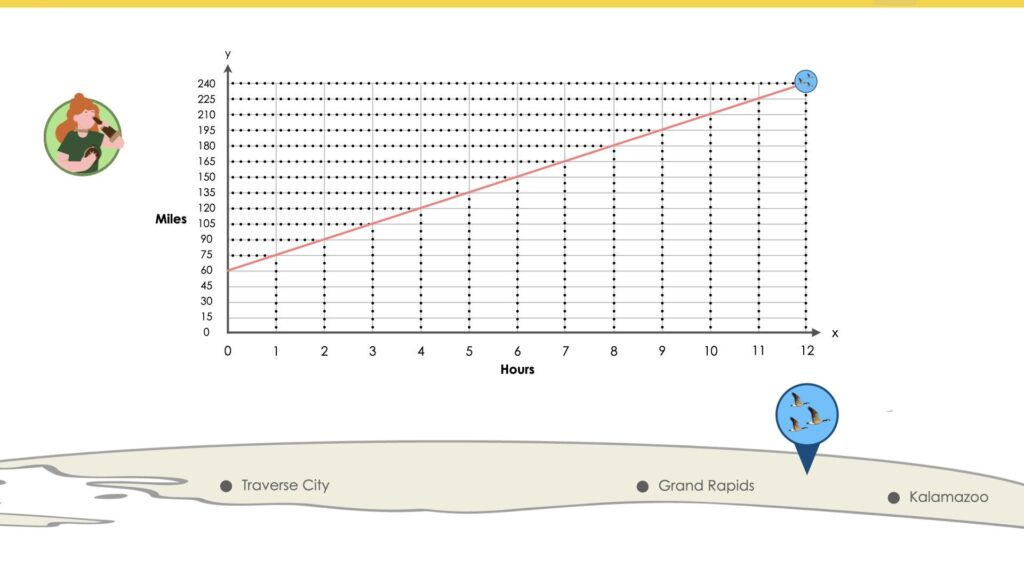
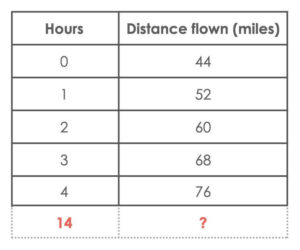
This particular flock of geese was spotted in Traverse City Michigan, where they were spotted by a local ornithologist. An ornithologist is a person who studies or is an expert on birds. When the flock was spotted, it was believed that they had already flown 60 miles across the top of Lake Michigan.
The ornithologist began tracking their flight pattern. She began recording their distance flown in the table below.
Student Prompt:
The ornithologist continued tracking the geese until they had flown a total of 240 miles south. Assuming the pattern continues, predict how many hours she will spend tracking this flock of geese.
Be sure to remind students that they are not to use a calculator to determine the number of hours as using that tool will rob them of this mathematical experience. Students should use a mathematical model in order to communicate their thinking.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Counting on
- Skip counting by 15
- Repeated addition
- Using multiplicative thinking
- Using division
Have students share their strategies and reasoning for how to represent the number of hours. Ask them to convince you and their peers that their answer is correct by sharing mathematical models.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
Student Approach #1: Skip Counting
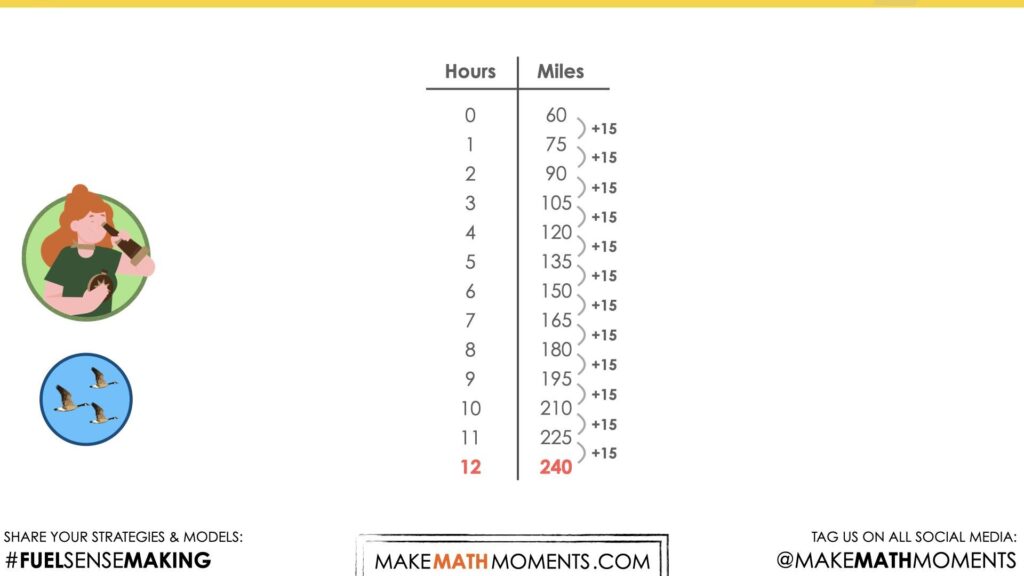
I started with the table that the ornithologist created. Then I realized that they were travelling 15 miles every hour, because 75-60 is 15, and 90 – 75 is also 15. So I just kept counting by 15 until I got to 240 miles. That happened on hour 12.
Student Approach #2: Subtraction & Quotative Division
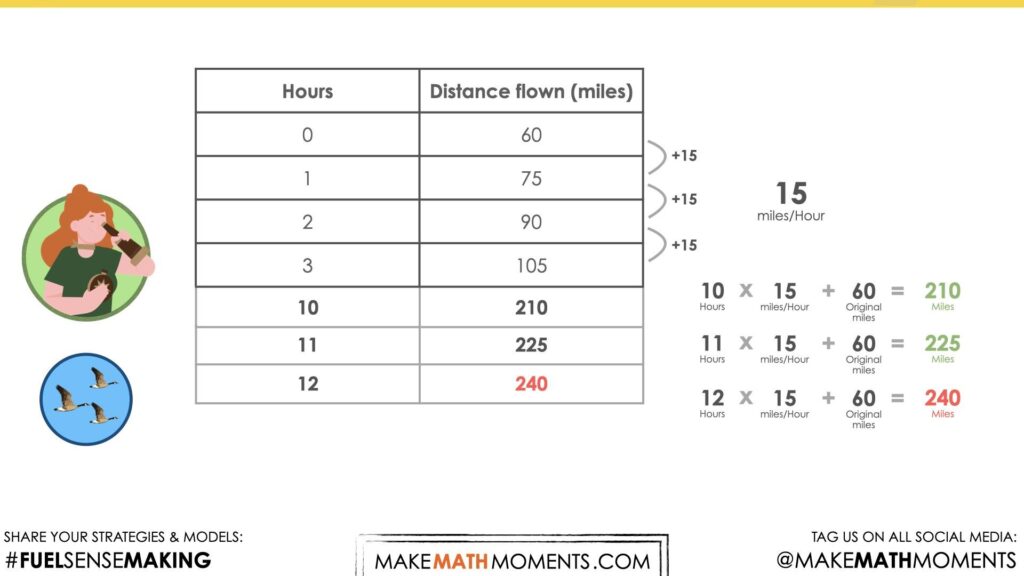
I took the 240 miles, and subtracted the original 60 miles. I had 180 miles left. I divided 180 by 15 miles/hour. I know it’s 15 miles every hour, because the pattern increases by 15. I did 150 divided by 15 is 10, and the remaining 30 miles divided by 15 miles per hour is 2 hours. That’s 12 hours altogether.
Student Approach #3: General Term
I realized that to find the distance, you multiply the hour by 15 miles and add the original 60 miles. I know it’s 15 miles every hour, because the pattern is increasing by 15 miles every time. So I found the distance for 10 hours. 10 times 15 miles, plus 60 is 210 miles. Not enough. So I tried 11 hours, still not enough. Finally, when I tried 12 hours, the number of miles was 240.
Next Moves
Consolidation
Consolidate your intentionally selected student solutions. Look for similarities in students’ approaches along the developmental continuum of counting, to addition and eventually multiplicative thinking.
Consider how students went about extending this pattern or using calculations to predict the hour that would record a total distance of 240 miles.
For example, some students may have used additive thinking to create and extend a table or graph.
Other students might have recognized that the pattern of repeatedly adding 15 miles is the same as a rate of 15 miles per hour (or 15 miles/hour).
Some students may have recognized that they could determine how many miles were travelled after they began tracking the flock by subtracting 60 miles from 240 miles, which left us with 180 miles travelled at a rate (or speed) of 15 miles per hour. We can then divide 180 miles by 15 miles per hour leveraging a strategy such as partial quotients where the 180 miles are decomposed into smaller, more friendly parts for dividing such as 150 miles and 30 miles.
Using trial and error with the equation to extend the table is also a common strategy students might consider applying to this problem:
Consider asking students the following question:
How would you describe this pattern in words?
Students might be able to articulate that they started at 60 miles, and then added 15 miles each time. Others may be able to describe this pattern using multiplicative thinking, seeing the relationship between x and y. Multiply the hour by 15 miles, and add the 60 miles they had already flown. Help students see both pattern rules in the table of values.
Consider asking students the following question:
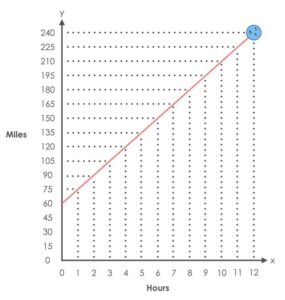
If we were to plot each number in this pattern on a graph 60, 75, 90, 105…), where the x-axis is the number of hours, and the y-axis is the distance of miles travelled, what shape will the graph take?
Give students an opportunity to reflect on this question and turn and talk. Allow students the opportunity to share and defend their thinking.
Students will notice that the points of this graph create a straight line that is increasing. Ask them to articulate why they believe that is. Land on the big idea that this is a growing linear pattern, because it increases by the same rate every time. This pattern however is unique in the fact that it does not start at 0. This pattern has an initial value, or constant of 60.
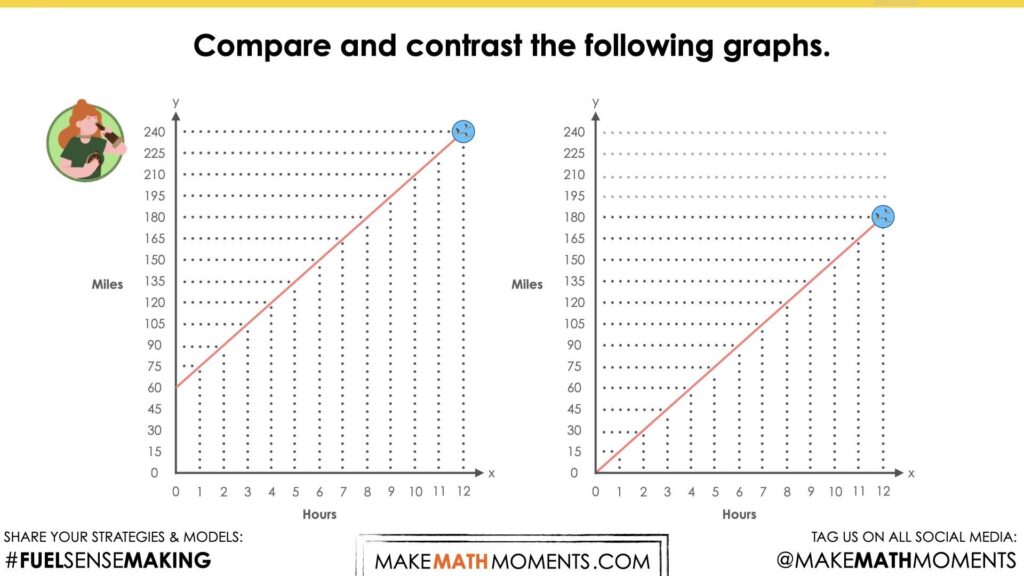
Show two graphs side by side, and ask students to:
Compare and contrast the following graphs.
We want students to articulate that in our context (graph 1), the initial value is 60. In graph 2, the initial value is zero. The initial value is where the line crosses the y-axis.
Facilitator note: In today’s graphical representation, the dots are connected. Both hours and miles are continuous data, they can be measured and there are quantities (including fractional amounts) that exist between each interval on both the x and y axis.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering this consolidation prompt to be completed independently.
Consolidation Prompt #1:
In today’s context, we explored a linear growing pattern with a rate of 15 and an initial value of 60. In your own words, explain those two key terms: rate and initial value.
Consolidation Prompt #2:
f this pattern continues, predict how miles will have been travelled on hour 14. Justify your answer.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!