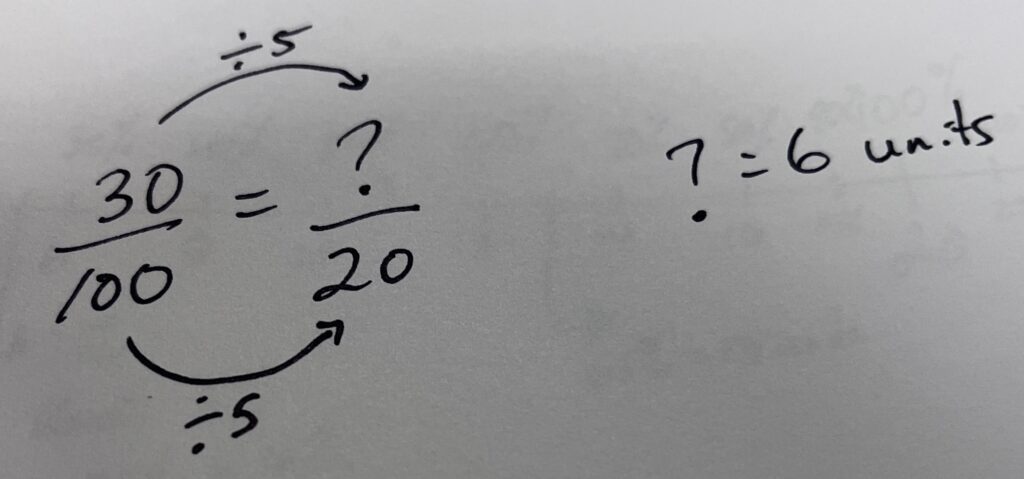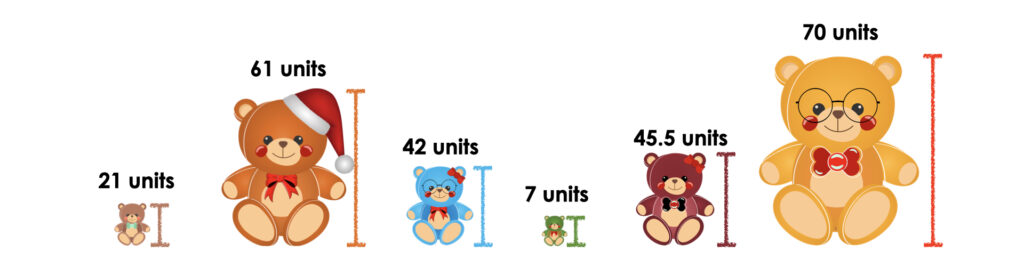BEAR BUILDER
CALCULATING PERCENT
Create and draw bears that vary in size.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will calculate the height of bears given various percentages of a base bear utilizing various strategies that build fluency in solving proportions.
Intentionality…
In this task, students will explore strategies to determine percentage values. They will make use of a double number line and benchmark percentages like 50%, 25%, 10%, 1% and multiplicative relationships to determine heights of various bears. Some of the big ideas that may emerge through this task include:
- Percent is a ratio.
- Percent is a comparison measured out of 100;
- A rate can be helpful to determine percentage values.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group.
Some of the noticing and wondering that came up in a class recently included:
- I notice a variety of bears..
- Some bears are shorter than the main bear and some are taller.
- I wonder how tall these bears are?
- I wonder how these bears relate to math class?
- Are any bears the same height?
Estimation: Prompt
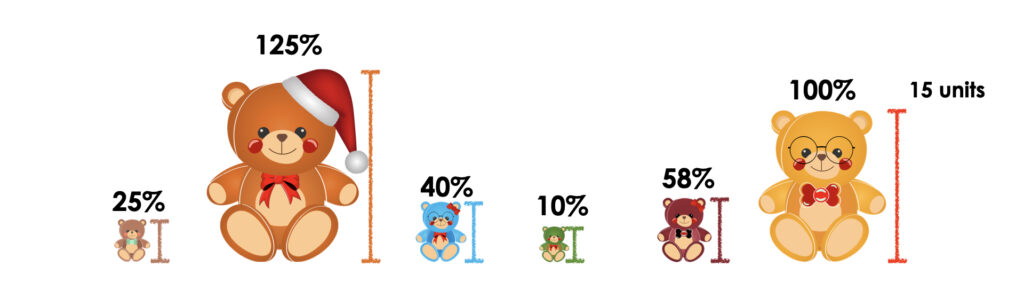
Next, share the following visual prompt briefly and ask the following question:
What are the heights of all the bears shown?
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Since you have already taken some time to set the context for this problem and student curiosity is already sparked, we have them in a perfect spot to help push their thinking further and fuel sense making.
Share the following silent animation.
You can verbally share the following prompt with students:
Determine the height of each bear shown in this image.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Encourage students to use precise mathematical language and listen for the use of both fractional language and percent to describe how the bears relate to the height of the base bear. Some students may compare the heights of bears to less than half, more than half, or equal to half of the height of the base bear. This should be brought out in discussion as it will aid your later discussion around benchmark percentages.
Allow students to share their estimates with neighbours first, then with the class. Write down their estimates on the chalkboard/whiteboard/chart paper so students feel their voices are being heard and so they feel they have a stake in solving this problem.
Lead the class in a discussion about what information is needed if they were to create more accurate estimations.
Ask: “If we were going to create a stronger, more accurate estimate what information would we need?”
Allow students to share their thinking with an elbow-partner or group before sharing with the class.
When students share with the class their thoughts on what information is needed, ask the key follow up question.
Key Follow Up Question: “If we gave you that information, what would you do with it to help narrow your estimate?”
Student Approaches
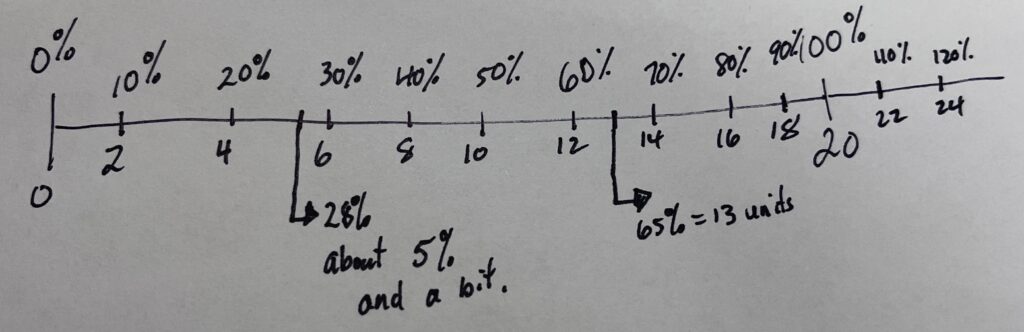
Student Approach #1: Benchmark Comparisons & Counting Up
I used 20 cubes to represent the height of the base bear. Then I split the cubes into two groups. So I knew 10 units was half so 50%. Then I split each of those groups into two groups so 25% was 5. I then knew that 5 x 5 is 25, so each unit is 5%.
Counting every unit block as 5% I counted by fives to realize that
30% = 6 cubes = 6 units
40% = 8 cubes = 8 units
120% = 20 cubes + 4 more cubes = 24 units
65% = 13 cubes
For 28% I know that 25% is 5 units tall. I need 3 more percent.
5% = 1 unit.
so 1% is 1/5th of a unit.
So 3% is 3/5ths of a unit.
So 28% = 5 units plus 3/5ths of a unit or 5.6 units tall.
Student Approach #2: Scaling in Tandem to 100
I divided 100% up into ten 10% chunks and represented that on a double number line.
Scaling every 10% = 2 units I could determine all the heights except the 28% bear.
Since 28% is close to 30% the height of that bear is just over 5 units tall.
Student Approach #3: Using Equivalent Ratios
For the bear that is at a height of 30% of the base bear’s height I know that 30% means 30 out of 100 so I need to determine the equivalent ratio out of 20.
After setting up the proportion I can see a scale factor of 5 between 20 and 100. Using the scale of 5 in reverse means 30 divided by 5 to give me 6.
The height of this bear is 6 units. I used a similar strategy to determine the other bear heights.
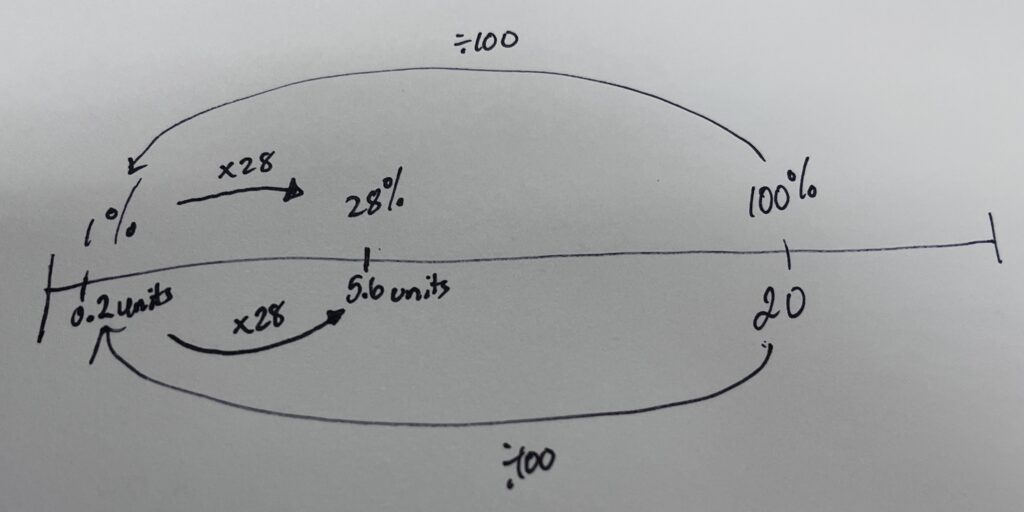
Student Approach #4: Making Use of Unit Rates
I found the number of units per 1% (a unit rate) for the base bear. 20 / 100 = 0.2 units per 1% . For the bear that is 28% of the base bear’s height I multiplied that unit rate of 0.2 units / 1% by 28 to get 5.6 units.
Next Moves
Consolidation
During the consolidation, review the strategies for determining the heights of the various bears.
Some students may have discovered that scaling percentages along a double number line can be helpful in determining many different percentage values.
Consider sharing the following consolidation video.
It is important to highlight that when we can scale both the percentage of bear height and the bear height in units these two ratios are equivalent. For example 6/20 = 30/100. Both 6/20 and 30/100 represent three-tenths of the base bear height, or 30% of the base bear height.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering this consolidation prompt to be completed independently.
Consolidation Prompt #1:
A new base bear is 15 units tall. Determine the heights of the bears that are around it.
Consolidation Prompt #2:
A new base bear is 70 units tall. Determine how tall each bear is as a percentage of the base bear’s height.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!