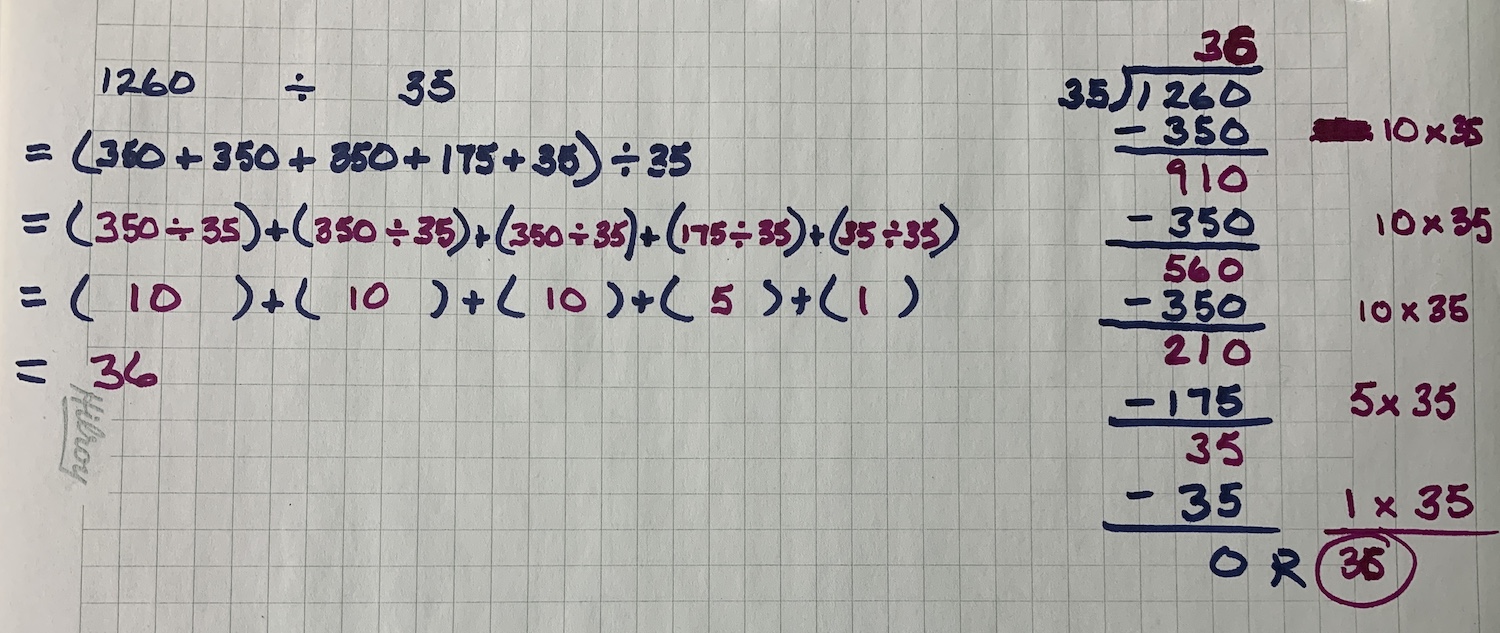WHIRLPOOL AERO CAR
MULTIPLICATION & DIVISION WITH WHOLE NUMBERS & DECIMALS; SOLVING EQUATIONS
Solving problems involving multiplication and division with whole numbers and decimals extended to solving equations.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will determine how many hours it will take to move 1 260 passengers in a single day of operation.
Intentionality…
Students will explore context which includes two quotative division contexts. First, they will determine the total number of trips needed to take 1 260 passengers in a single day.
They will know the total number of passengers and the numbers of passengers per trip (a rate). They will determine the number of trips (or parts). They will use this information to solve a second quotative division probably. How many hours will it take to make that number of trips.
Some of the big ideas that will likely emerge in this task include:
- Multiplication and division are related.
- There are two types of division.
- Quotative (or measured) division reveals the numbers of parts when the rate is known.
- The dividend from any division sentence can be decomposed into smaller parts to allow for friendlier division by the divisor. This strategy is known as partial quotients. (i.e.: 85 ÷ 5 = 45 ÷ 5 + 40 ÷ 5 = 9 + 8 = 17).
- Partial products, made possible by the distributive property, allows one or both of the factors to be decomposed in order to simplify a multiplication sentence.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Replaying the video and/or leaving a screenshot from the video up can be helpful here.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group. Be sure to write down these noticings and wonderings on the blackboard/whiteboard, chart paper, or some other means to ensure students know that their voice is acknowledged and appreciated.
Some of the noticing and wondering that may come up includes:
- I notice a body of water.
- I wonder where it is.
- I notice some large cables.
- I notice something suspended on the cable.
- I notice that it is yellow and red.
- I wonder where they are going.
- I wonder if there are people on the ride.
- I wonder how many people.
- I wonder how long it takes to get across.
- I wonder what is on the other side.
At this point, you can answer any wonders that you can cross off the list right away. For example:
- This Whirlpool Aero Car is in Niagara Falls, Ontario, Canada;
- The cable car is located in Niagara Falls, Ontario that transports passengers over a section of the Niagara River referred to as the Niagara Whirlpool.
- The system was designed by Spanish engineer Leonardo Torres Quevedo and has been upgraded several times since 1916 (in 1961, 1967 and 1984).
- The system uses one car that carries 35 standing passengers over a one-kilometre trip.
- The cost is $16.50/adult and $10.75/student.
Estimation: Prompt
After we have heard students and demonstrated that we value their voice, we can land on the first question we will challenge them with:
How long does it take to travel to the other side and back (one roundtrip)?
Make an estimate.
You might choose to share this short clip giving them a perspective of how fast the Aero Car moves.
Share the following animation and prompt students to update their estimates:
Consider leaving the following screenshot of the final frame of the animation up for students to see.
We can now ask students to make an estimate (not a guess) as we want them to be as strategic as they can possibly be. This will force them to use relative thinking and proportional reasoning based on the information that has been shared.
Consider asking students to think about a length of time that would be “too low” and a length of time that would be “too high” before asking for their best estimate in order to help them come up with a more reasonable estimate. Encourage students to share their estimates, however avoid sharing their justification just yet. We do not want to rob other students of their thinking.
While Students Are Estimating
Listen and observe as students work to make their estimates. Are students using spatial and proportional reasoning?
Are they using fractional and multiplicative language to describe the distance travelled by the car in the video relative to the entire trip? Are they considering the ratio that exists – distance travelled: time, and using appropriate units and mathematical language?
Estimation: Reveal
Consider sharing this video of the Aero Car travelling one-way across the Whirlpool in 300 seconds (600 seconds round-trip):
You might consider sharing this animated video of the Aero Car travelling round-trip:
A screenshot you might consider sharing as well:
Answer: 600 seconds round-trip.
Celebrate student estimates that were very close to the actual number of riders using a routine of your choice as we head into the sense making portion of this lesson.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Share that in a single day of operation, 1 260 passengers rode the Whirlpool Aero Car, with each ride at maximum capacity of 35 passengers.
Prompt students by stating:
How many hours was the Whirlpool in operation today to accommodate 1 260 passengers?
Be sure to remind students that they are not to use a calculator to determine the total length of time.
As a reminder, it took 600 seconds or 10 minutes for 1 round-trip ride on the Whirlpool Aero Car. You may choose to withhold this information to allow students to independently pull this information from their prior work before doing this thinking for them by giving the information to them.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- An array through skip counting
- An open-array using partial products
- Partial products on a numberline
- A flexible algorithm using partial products
Have students share their strategies and reasoning for how to represent the length of time that the Aero Car was in operations. Ask them to convince you and their peers that their answer is correct by sharing mathematical models.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
Student Approach #1: Array with Partial Products Over Addition & Subtraction
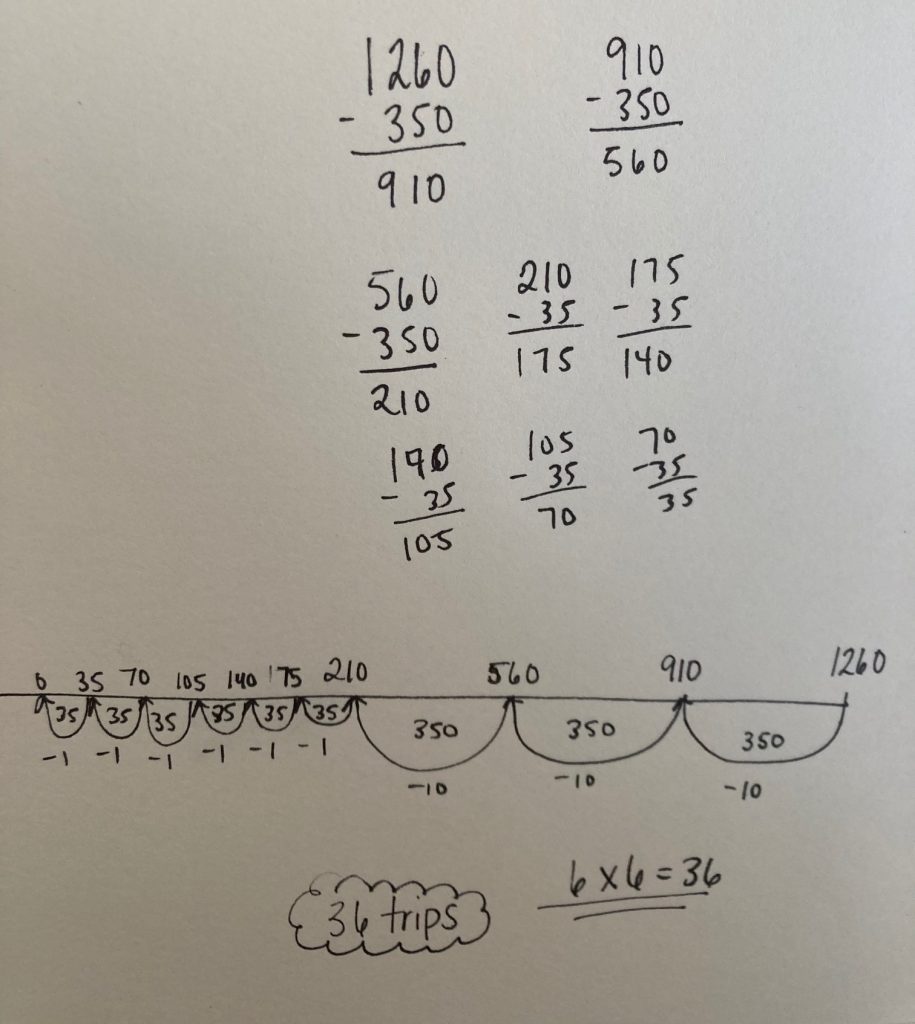
I started with 10 trips of 35 passengers. That’s 350 passengers, I added 350 more, again, and again. I had 40 trips with 1 400 passengers, which was too many. I realized that 1 400 is 140 more than I needed, which is the same as four trips, so I subtracted four trips. They made 36 trips. I know that they can make 6 trips in one hour, so that is 6 hours of operation.
Facilitator Note:
This student used partial products over addition and over subtraction to solve this quotative division context.
(10 + 10 + 10 + (10-4)) x 35
Student Approach #2: Repeated Subtraction on a Number Line
I know that there were 1 260 passengers in a day, and that each ride can have 35 passengers. I started with 10 rides, because I know that 10 times 35 is 350, and I worked backwards. I kept taking away rides until there were no passengers left. I used subtraction and I showed my thinking on the number line.
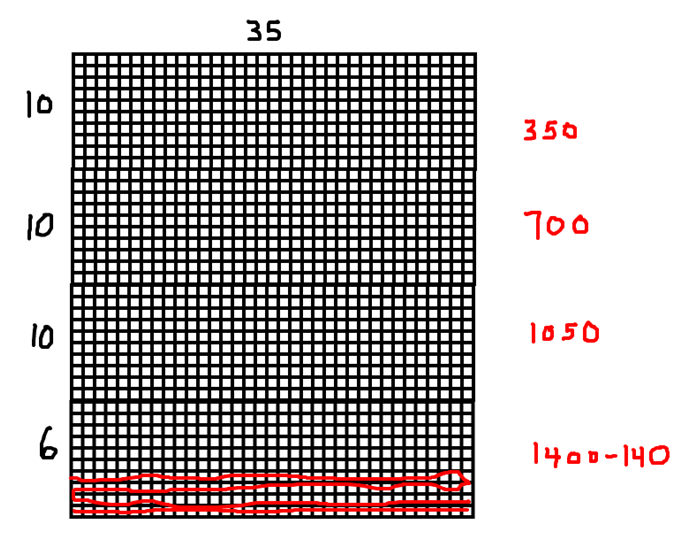
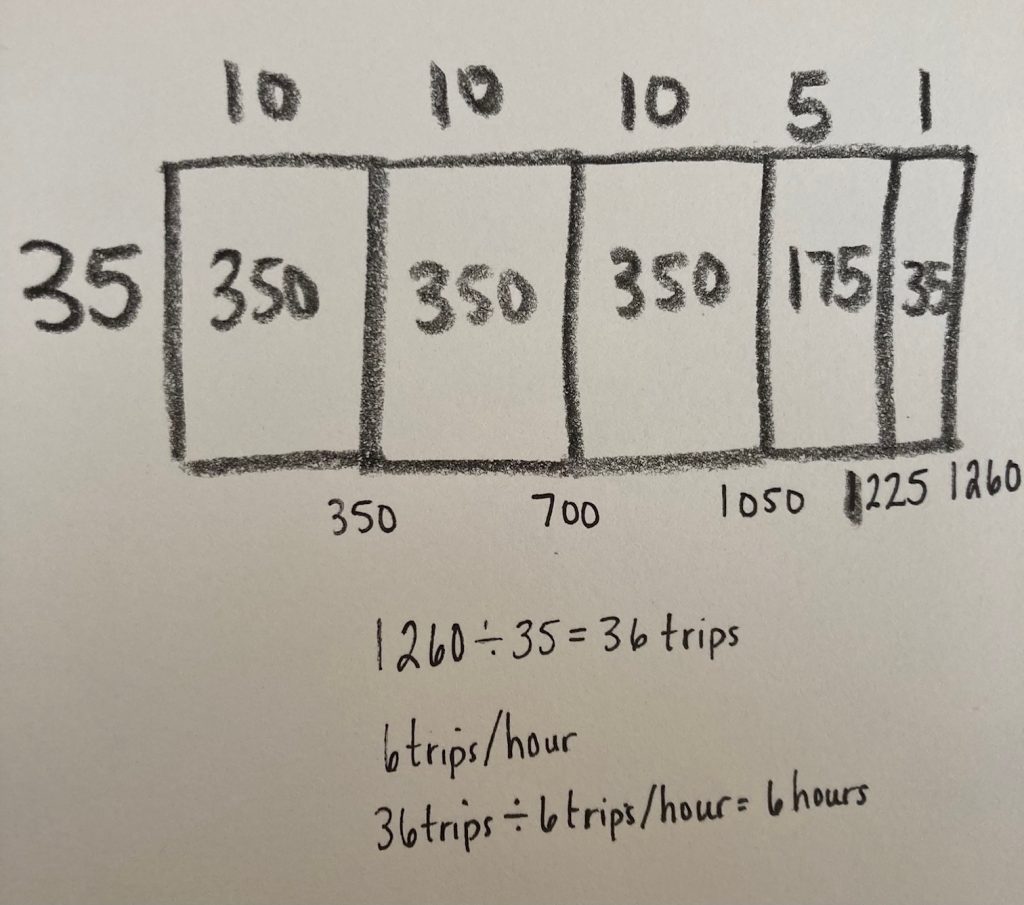
Student Approach #3: Partial Products Over Addition in an Open-Array
I used an open array to keep track. I started with 10 trips, then added on 10 more until I had 30 trips which was 1 050 passengers. I realized another 10 would be too many. I added 5 more trips for a total of 1 225 passengers, one more trip gave me 1 260 passengers, so that’s 36 trips altogether. Because each trip takes 10 minutes, they can make 6 trips in an hour. So 36 trips divided by 6 trips per hour means they would need to have the Aero Car running for 6 hours that day.
Next Moves
Reveal
Once the lesson has been consolidated emerging the big ideas that multiplication and division are related including their helpful strategies of partial products and partial quotients in this quotative division context, you can share the following reveal video:
You might also consider sharing the following reveal image:
Consolidation
Begin by asking students the following prompts:
Prompts:
What operation was used today to solve this problem?
With student input, land on the following division sentences:
1 260 passengers ÷ 35 passengers per trip = 36 trips
36 trips ÷ 6 trips per hour = 6 hours
Highlight which information was known and the information you were seeking in order to reveal that both contexts were “quotative” division contexts.
Quotative Division:
Dividing a dividend into a measured quantity (or known rate). In this type of division, the size of the groups is known (35 people), the number of parts is unknown (the number of trips).
Highlight the relationship between multiplication and division through this context. Likely, many students relied on repeated addition or partial products in order to determine the number of trips. After determining the number of trips required to be 36, determining the number of hours was likely a known-fact for many students.
There may be an opportunity to explore partial products over addition and over subtraction depending on how students went about determining the number of trips. Did they go past 36 and work back? Did they get close and then work up? How did students take jumps, by one group of 35? By ten?
In the following silent solution animation video, you will see an approach that leverages a partial products strategy through distribution over addition both visually with an area model as well as symbolically highlighting the use of brackets:
Partial products were created with this particular approach by adding “parts” of one factor (which, in this context is actually the quotient we are solving for) and adding the partial products until reaching the product of 1260 (which again, is our dividend for this division problem).
Modelling over subtraction could be done in numerous ways including, but not limited to:
35(10 + 10 + 10 + 10 – 4)
Which is equivalent to the following four partial products:
(35 x 10) + (35 x 10) + (35 x 10) + (35 x 10) – (35 x 4)
Note that a student leveraging this strategy might notice that 35 x 10 is iterated 4 times:
4(35 x 10) – (35 x 4)
Simplifying further:
4(350) – (35 x 4)
If students are forced to evaluate leveraging strategies and models without a calculator (as we always suggest), then you might see some students break this down even further:
4(300 + 50) – (70 x 2)
Notice the decomposing of 350 into two parts; 300 and 50 as well as a doubling and halving strategy applied to double 35 and half 4 resulting in an easier calculation of 70 x 2. Then, students may be able to finalize their computation as something like:
(1 200 + 200) – (140)
While some students will jump on adding 200 to 1 200 for a quick and easy sum of 1 400, some students might see the associative property of addition and subtraction as helpful to quickly subtract 140 from 200.
1 200 + (200 – 140)
Resulting in:
1 200 + 60
= 1 260
Connecting Partial Products to Partial Quotients
Anticipating that some students will leverage partial products as a strategy to “add up” by groups of 35 passengers until reaching the dividend of 1 260, be sure to connect the idea that division works in a related way.
While many students may have used the partial products multiplication strategy as a tool for thinking to reveal the unknown number of trips:
35(x) = 1 260
Then, using known facts to continue growing the product until reaching 1 260:
35(10 + 10 + 10 + 5 + 1) = (350 + 350 + 350 + 175 + 35)
35(10 + 10 + 10 + 5 + 1) = 1 260
A similar approach can be used to solve this problem using division:
1 260 ÷ 35 = x
Although students who used partial products slowly composed one of the factors until reaching the product of 1 260, students who apply this strategy to division will find themselves decomposing the dividend of 1 260 into smaller parts to make quotative division by 35 easier. Almost automatically, students leveraging this strategy might decompose 1 260 into as many 350 parts since it is likely that the division fact of 350 ÷ 35 = 10 is automatic.
(350 + 350 + 350 + 175 + 35) ÷ 35 = x
(350 ÷ 35) + (350 ÷ 35) + (350 ÷ 35) + (175 ÷ 35) + (35 ÷ 35) = x
(10) + (10) + (10) + (5) + (6) = x
36 = x
While some educators feel overwhelmed thinking of division outside of the long division algorithm that many of us learned ourselves as students, it should be noted that long division is built off of the partial quotients strategy. While the “rules” that we were taught tell us that we are looking for how many times the divisor “goes into” the dividend, working our way from the largest place value digit to the smallest, partial quotients offers a more flexible approach to arrive at the same result.
This flexibility makes emerging the strategy of partial quotients much more accessible for all students unlike the very rigid approach of teaching the “rules” of long division.
Look at the partial quotients strategy (on the left) and a more flexible long division strategy on the right:
In both cases, students are the decision makers on what size chunks or “parts” they would like to decompose the dividend into which will also yield more opportunities for all students to practice and extend their known multiplication and division facts.
Facilitator Note: What About Long Division?
Please do not pre-teach the long division algorithm and work “backwards” to partial quotients. If your local curriculum explicitly requires the teaching of the common long division algorithm, then please ensure that students have fluency and flexibility with both types of division and strategies such as partial products before extending the structure to long division.
As an aside, the Common Core State Standards mention using the standard algorithm or long division beginning in grade 6:
Fluently divide multi-digit numbers using the standard algorithm.
Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
While we do not advocate teaching division with an end goal being a “standard algorithm”, if your standards require an algorithm be used, ensure that you are not rushing there and that many connections are made along the journey.
If students have already been pre-taught long-division, then it is more challenging for strategies like partial quotients to emerge more naturally. You will likely need to assist in making these connections.
Facilitator Note: What About Factoring The Divisor?
While unlikely students will go this route based on the context and the added complexity given the quantities we are dividing, it is worth noting that decomposing the dividend is not the only way students could go about dividing. As the facilitator, it is important that we understand that we cannot simply decompose the divisor like we did to the dividend in the previous example.
If we ignore the context, we can leverage partitive division (instead of quotative division as this context calls for) to partition the dividend of 1260 passengers into 35 trips which reveals 36 passengers per part. While the resulting number of 36 is correct, the unit should be 36 trips (not passengers per part). Continuing with this approach, the partitioning of the dividend can be found more easily by factoring the divisor of 35 into 5 and 7. Then, 1260 can be partitioned by 5 and then by 7 (or visa versa) instead of decomposing the dividend as we shared above.
As mentioned, it is helpful for facilitators to understand that when we use partial products, decomposing the dividend lends itself to quotative division, while factoring the divisor lends itself to partitive division.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt:
Consider the following statement:
Quotative division problems can be solved through multiplication.
Prove that this statement is true.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!