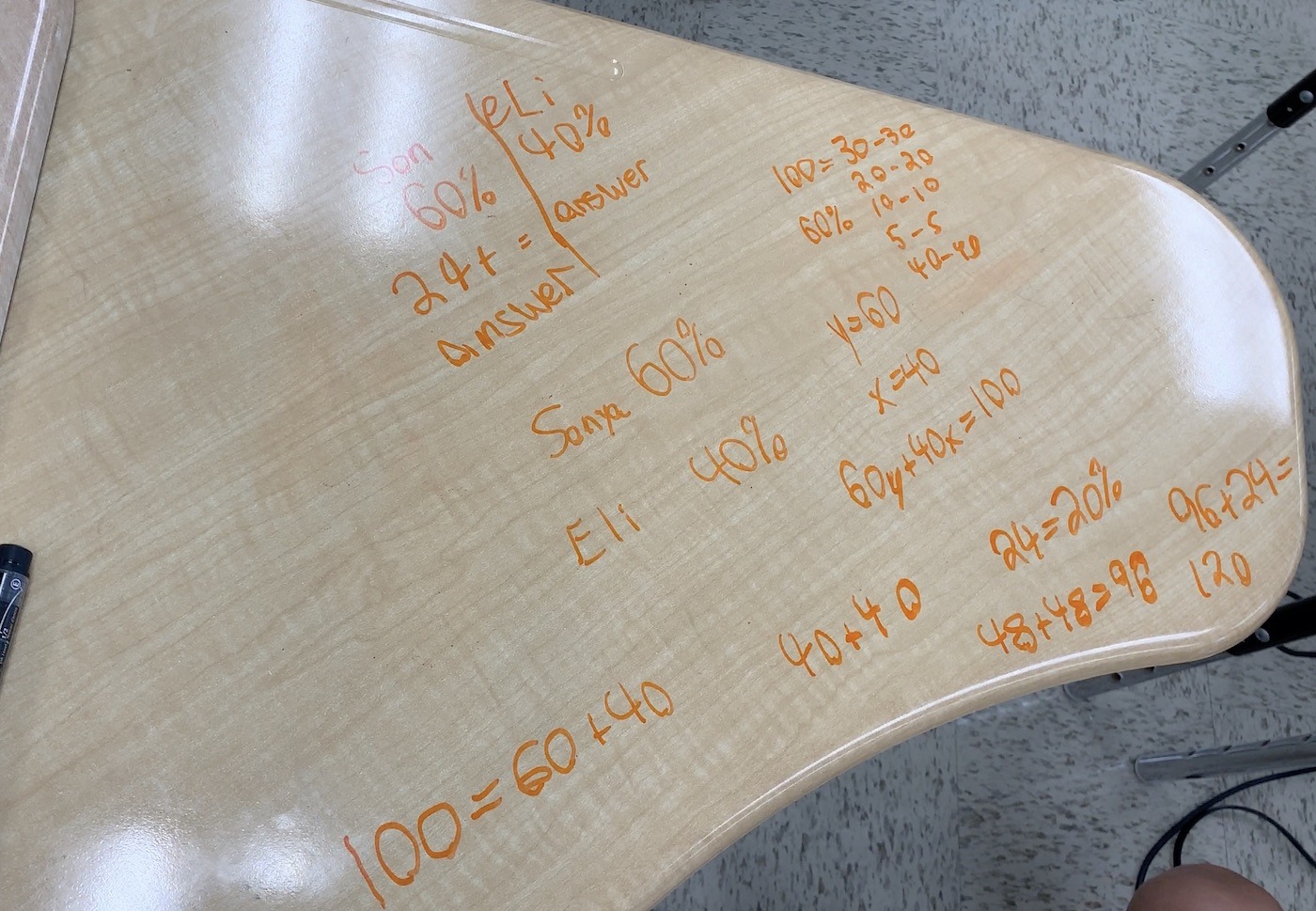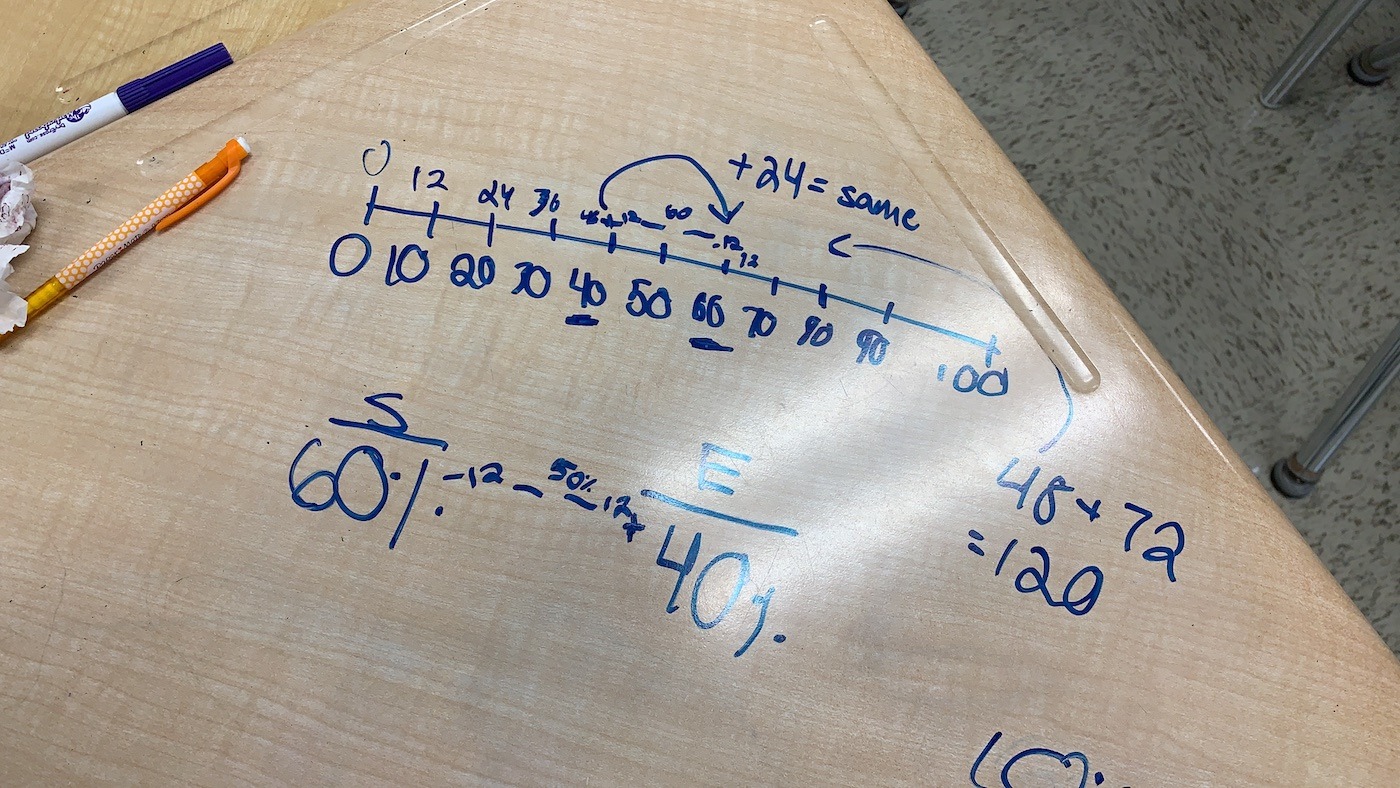VOTING BOOTH
PROPORTIONAL RELATIONSHIPS, PROBABILITY AND PERCENT
Use percentages to explore proportional relationships and extend to solving equations.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Investigate problems involving proportional reasoning including percentages with the possibility of extending to creating and solving equations.
Intentionality…
In this task, students will investigate a problem involving a student council vote between two candidates where they will be required to reason proportionally using percentages. This task will allow students to develop a deeper understanding of big ideas related to percentages including the following:
- A part of a whole represented as a percentage is a part-whole ratio whose whole is 100;
- A percentage is one of infinitely many equivalent part-whole ratios in a ratio relationship;
- Quotative division can be used with percentages to scale in tandem and reveal an infinite number of equivalent ratios in a ratio relationship; and,
- Partitive division can be used to divide a percentage by 100 percent to reveal a rate for the proportional relationship.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the video below showing someone writing “Sonya” on a piece of paper and placing it into a cylindrical container.
Ask students to engage in a notice and wonder protocol. ANYTHING and EVERYTHING that comes to mind is fair game.
Write down all of the noticing and wondering from your students. For example:
- Black marker
- Who is Sonya?
- Sonya is only name in bucket.
- I saw a ring on his finger.
- Why all uppercase letters except for the ‘o’?
- Why only 1 piece of paper?
- Why? What does this have to do with math?
- Is this a probability game?
- Is this a vote?
- Why so many papers if you only needed 1?
- Is there other stuff in the bucket?
- And many others…
Take time to acknowledge the noticing and wondering your students have engaged in and try to answer any that you can address right away.
Then show video 2 where you will see a second name, Eli, written on a paper prior to seeing those two names repeatedly written and placed in the container:
Prompt:
At this point, it will become clear to everyone that this is a vote and the question we will land on is:
How many people voted?
Give students an opportunity to make an estimate by first thinking independently and then having them share their estimate with a neighbour.
Ask students to estimate a number of square tiles that they think is too low and a number of square tiles that they think is too high before making their “best estimate”.
After sharing out estimates and recording them on a number line, ask students what information they could use to make their original estimates more precise. You might even consider sharing a few additional images like this zoomed in version of the image to see the pile of ballots that represents the total number of votes that will be cast in this student council election.
Another optional image you might consider sharing to give students a better spatial perspective:
Sorting The Votes
Students can now see the votes being sorted, but not counted. The pile of Sonya votes (left) next to Eli votes (right) will make it apparent that Sonya has won the vote, but by how much?
Let’s give students another opportunity to update their estimates.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
After they brainstorm and share out, show the video below: Follow up with:Update your estimate. How might we convince someone that the quantity you come up with is reasonable without the use of a calculator?
 Students have now been given enough information to now make calculations using mental math to improve their estimates based on spatial reasoning and/or prior knowledge.
Students have now been given enough information to now make calculations using mental math to improve their estimates based on spatial reasoning and/or prior knowledge. During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Connecting cubes in order build two equivalent expressions.
- Area models.
- Double number lines.
- Symbolic representations.
- As well as others.
Have students share their strategies and reasoning for determining how many total votes including how many votes Sonya received as well as how many votes Eli received. Ask them to convince you and their peers that their answer is correct by sharing mathematical models.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
Student Approach #1: Area Model and Scaling In Tandem
I wrote out rectangles to represent the different vote totals for Sonya and Eli. Since Sonya received 60% of the total votes and Eli received 40%, I drew a rectangle to represent Eli’s total votes on the right of my desk.
Then, I drew two rectangles on the left side representing Sonya’s 60% of the total vote; one rectangle to represent 40% of the total vote and another rectangle to represent the 24 extra votes Sonya received. Since Sonya received 60% of the total vote, I know that the 24 extra votes must be equal to 20%, which basically solved the problem for me.
That means I can double it to get Eli’s 40% (or 48 votes).
Then, I just have to add another 20% to Eli’s 40% to get Sonya’s 60% (or 72 votes).
Add Sonya and Eli’s votes to get 120 total.
Model & Strategy
This student used an area model as a tool for thinking and to represent her thinking. Her strategy was both multiplicative (doubling 20% to find the number of votes equivalent to 40% of the total) as well as additive (adding an additional 24 to find Sonya’s vote total). When we double 20% to 40% and 24 votes to 48 votes, this scaling in tandem is commonly referenced as ratio reasoning by many including the Common Core Standards authors.
Student Approach #2: Symbolic Guess and Check
I tried to create an equation, but I couldn’t figure it out.
So then, I started to play with the numbers until I realized that the 24 vote difference between Sonya’s vote total and Eli’s vote total must also represent 20% of the total. This is because the difference between Sonya’s 60% of the total votes and Eli’s 40% of the total votes is 20%.
From here, I doubled 24 to get 48 votes which represents 40% of the total votes.
I doubled 48 votes to get 96 votes, which represents 80% of the total votes.
Adding 24 votes brings me to 120 total votes, representing 100% of the total votes cast.
Model & Strategy
This student used symbolic representations as a tool first to attempt constructing an algebraic equation, before shifting to a guess and check strategy. Thinking was both multiplicative (doubling) by scaling in tandem and additive to add 24 votes (or 20% of the total votes) to 98 votes (or 80% of the total votes) to arrive at the total.
Student Approach #3: Double Number Line to Scale In Tandem
I wasn’t sure what to do at first, but when my teacher asked me to try representing the quantities in the problem, I started with a number line. After some thinking, I realized that 24 votes represented 20% of the total votes. From here, I knew 0 votes represented 0% of the total votes. Then, I just added 24 votes and 20% until I got to 120 votes and 100%. It made sense because there are five 20%’s in 100%, so I could have just multiplied 24 votes by 5.
Model & Strategy
This student used reasoning and a double number line as a tool for thinking. This student used additive thinking to repeatedly add 20% and 24 votes to arrive at 100% and 120 votes before realizing that a multiplicative approach would have been clever.
Student Approach #4:
Since Sonya had 60% of the total votes and also had 24 more votes than Eli, that meant that Eli must have had 40% of the total votes.
Since the difference of 60% and 40% is 20%, then 24 votes must be equal to 20% of the total votes. If I half 24 votes and 20%, I get 12 votes and 10%. So if you took 12 votes from Sonya’s total and added them to Eli’s total, they would both have 50% of the votes.
Knowing this, I made a double number line and realized that if I label 24 votes as equivalent to 20%, then 12 votes must be equivalent to 10%. From there, I multiplied 12 votes by 4 to get 48 votes and 10% by 4 to get 40% for Eli’s votes and I did the same for Sonya, except by 6 to get 72 votes and 60%.
When I added the votes together, I got a total of 120 votes.
Model & Strategy
This student used reasoning and a double number line as a tool for thinking. Once this student realized that halving 24 votes and 20% of the total would reveal another equivalent ratio in this relationship of 12 votes and 10%, he used this knowledge to scale in tandem on the double number line.
Student Approach #5:
I know that 60% of the total is equivalent to 40% of the total plus an additional 24 votes, but I’m not sure what to do from here.
Model & Strategy
This student used a symbolic representation by constructing an algebraic equation, however was uncertain of how to solve the equation for the unknown variable, t. This student could probably use questioning to encourage the use of a more concrete or visual model.
For example, with connecting cubes, this student might be able to represent their thinking this way:
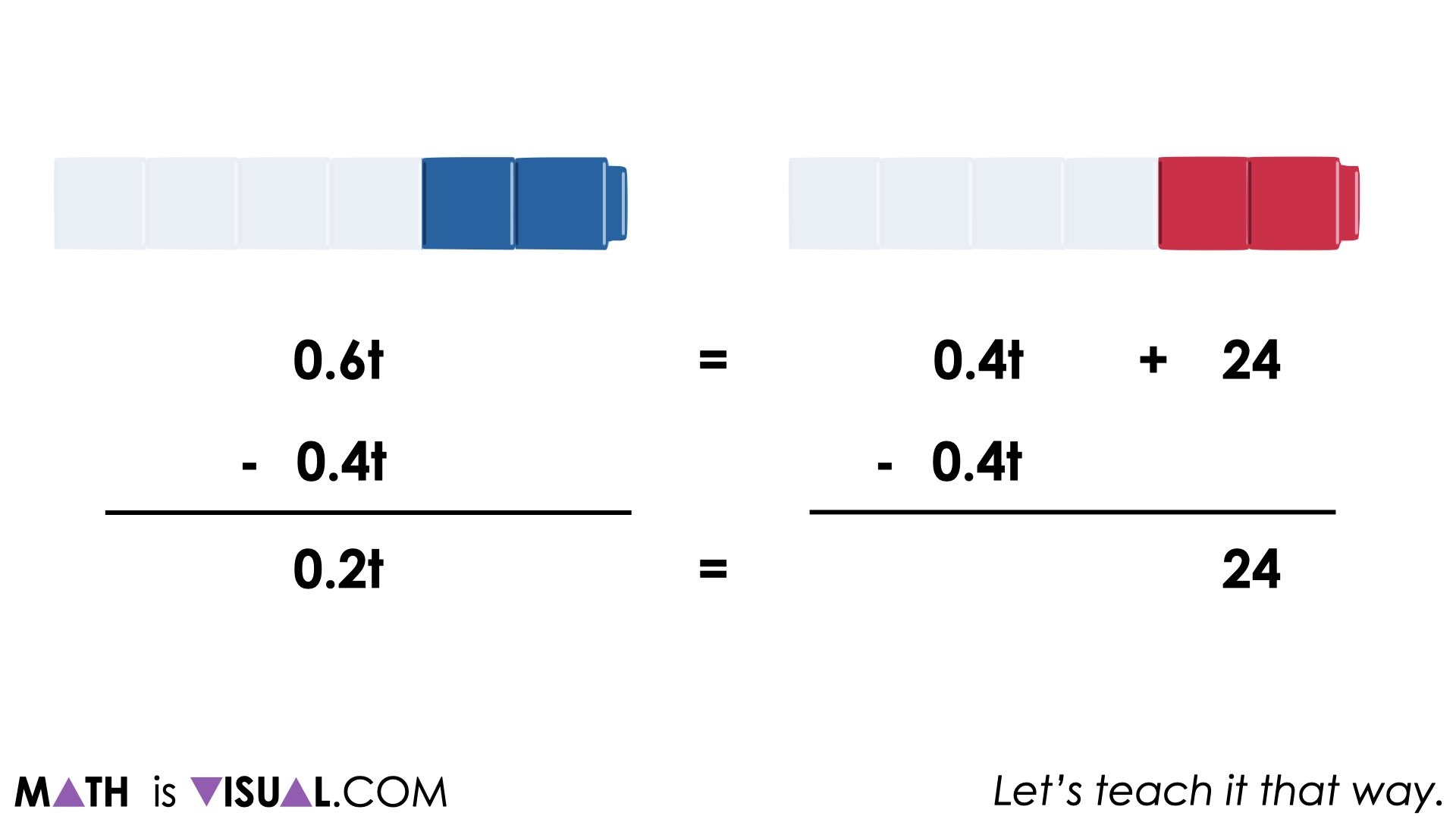
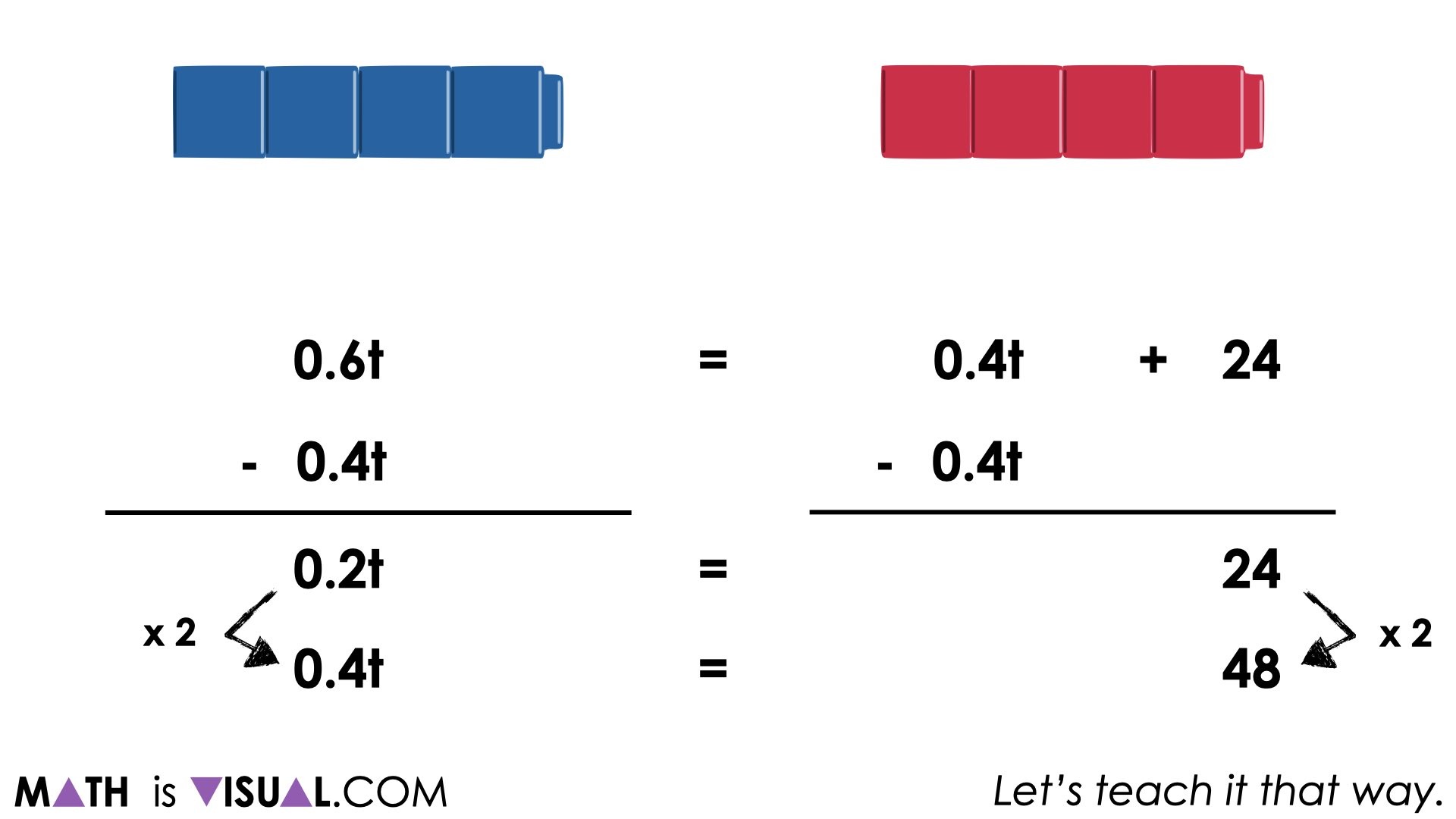
By subtracting 40% of the total votes from both sides of the equation, we still maintain equivalence:
From here, we can approach determining the total in a number of different ways. While “dividing the coefficient” tends to be a procedure we rush to teach students, I might encourage students using the same scaling in tandem approach that the other students used with their area models and double number lines.
For example, a student might choose to scale in tandem by doubling:
Then doubling again and finally adding an additional 20% and 24 votes:
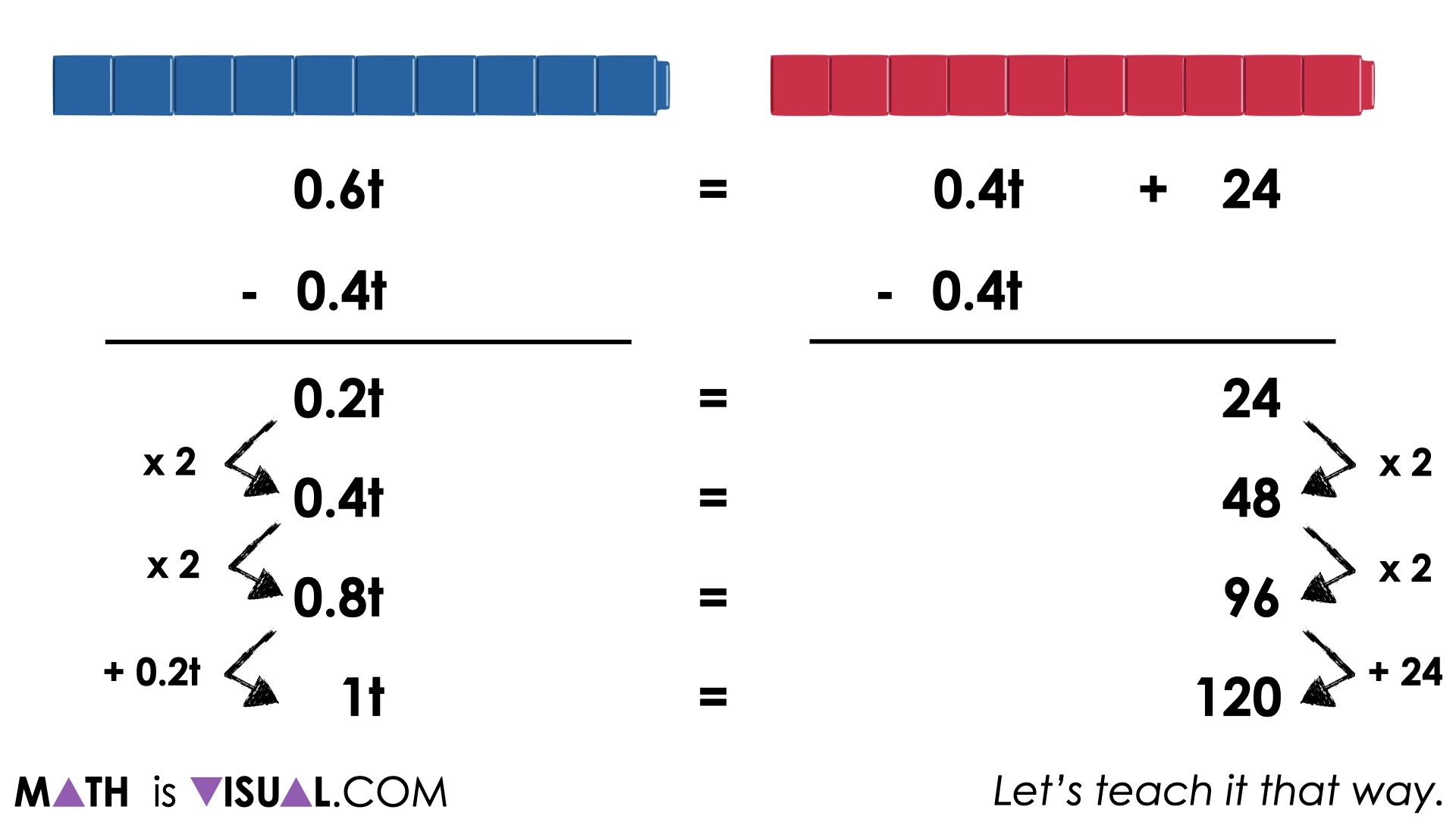
Other students may choose to simply scale by multiplying both sides by 5; from 20% of the total votes and 24 votes to 100% and 120 votes.
If a student chooses to divide by the coefficient, encourage them to convince you why this works. What is happening conceptually for this operation to work?
Next Moves
Consolidation
The purpose of the consolidation is to make connections between strategies and reveal and/or solidify big ideas.
Consolidate learning using student generated solution strategies based on what you selected and how you sequenced while monitoring during the Sense Making portion of the lesson.
In particular, use student work and purposeful questioning to highlight that the 60% of total votes that represents Sonya’s total votes and 40% of total votes that represents Eli’s total votes represents a 60:40 or 6:4 or 3:2 ratio relationship which can be helpful to solve using ratio reasoning.
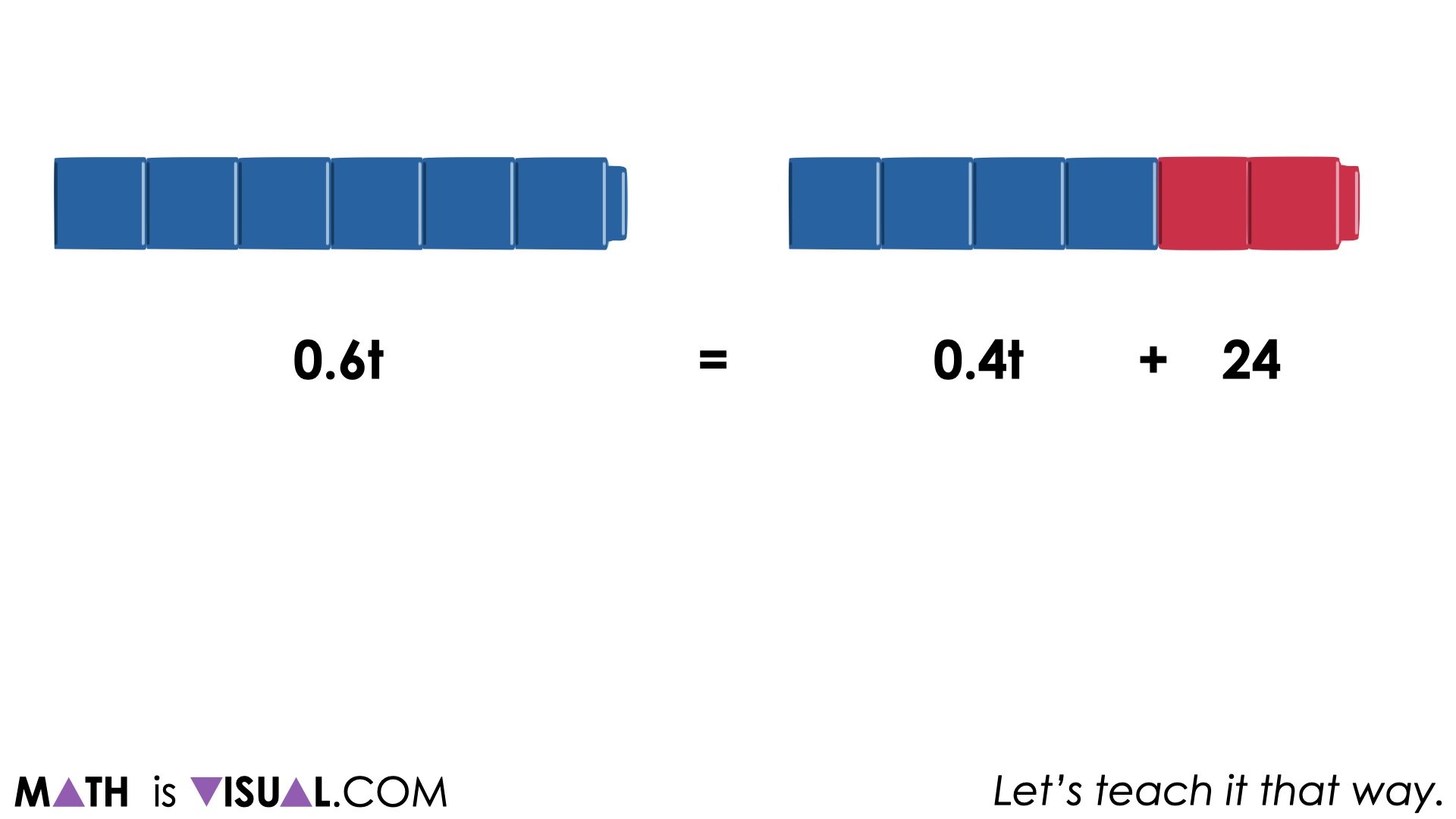
Furthermore, when we consider that 60% of the total votes, t, can be represented as:
(6/10)t or 0.6t
We can also think of 40% of the total votes, t, as:
(4/10)t or 0.4t
Since we know that Sonya had 24 more votes than Eli, we can use this information to create one of many possible equations:
0.6t = 0.4t + 24
Refer to the Student Approaches to view concrete examples using connecting cubes that make representing and solving this equation intuitive and accessible for all learners.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering this consolidation prompt to be completed independently.
Consolidation Prompt:
Your friend is counting votes for another position on student council and she claimed that of the 68 total votes, the successful candidate received 75% of the votes while the unsuccessful candidate received 32 less votes.
Determine without a calculator whether this scenario is possible and write a convincing argument explaining how you know.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!