SQUARES TO TRIANGLES
PYTHAGOREAN THEOREM
Dive into our problem based unit where we explore the Pythagorean relationship through area of squares & triangles.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
In this task, students will observe a small square inscribed in a larger square. Students will use their prior knowledge of areas of squares, rectangles, and triangles to determine the area of the inscribed square.
The purpose of this task is for students to apply their understanding and knowledge of determining areas of composite figures and congruence in a context that will allow them to bump into the Pythagorean relationship. Students will build fluency in determining areas of squares and triangles while recalling or realizing that congruent shapes occupy the same area before and after translations and rotations. Students will reflect and use the inverse relationship between the area of a square and the side length of the square.
Some ideas that may emerge through this task include:
- Area of composite figures;
- The Pythagorean relationship; and,
- Congruence.
- Translations / rotations.
- Squaring numbers and their square roots.
- The sum of the area of the squares constructed using the short legs of a right triangle is equivalent to the area of the square constructed using the longest leg.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Replaying the video and/or leaving a screenshot from the video up can be helpful here.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group. Be sure to write down these noticings and wonderings on the blackboard/whiteboard, chart paper, or some other means to ensure students know that their voice is acknowledged and appreciated.
Some of the noticing and wondering that may come up includes:
- There are two squares.
- Some line segments are equal and some are not.
- I see triangles and squares.
- I see a diamond.
- I wonder if those triangles are the same?
- I wonder if how much area is the big square?
- I wonder how much area is the smaller square?
Estimation: Prompt
After we have heard students and demonstrated that we value their voice, we can land on the first question we will challenge them with:
Show students the image below.
How many of the small squares will fit in the large square?
We can now ask students to make an estimate (not a guess) as we want them to be as strategic as they can possibly be. This will force them to estimate dimensions and use their knowledge of area.
Encourage students to share their estimates, however avoid sharing their justification just yet. We do not want to rob other students of their thinking.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Prompt students by asking:
If you were to have more information to help narrow your prediction/make your prediction more accurate what extra information would you want?
Engage your class in Think-Pair-Share where they Think independently on what they would like to have to update their prediction, Pair and share their thinking with a partner, finally share their thinking with the class.
Show the More Information images one at time pausing and prompting your students to share their strategies.
Image #1
Image #2
With this information and confirming that the largest square is in fact a square, ask students to update their prediction while showing their mathematical thinking.
You might also consider sharing this Mathigon Polypad virtual manipulative template so that students can interact with the figure as they update their original prediction.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Concrete materials.
- Using knowledge of areas of basic shapes.
Have students share their strategies and reasoning for how to determine the area of the inner square. Ask them to convince you and their peers that their answer is correct by sharing mathematical models.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
Student Approach #1: Linking cubes and area of a square
I made an outline of the square with cubes. I determined that the side lengths of the inner square were 20 by 20. Since the area of a square is length x width, the area of the inner square must be 20×20 = 400 square units.
Student Approach #2: Area of Triangles & Area of Squares
I subtracted the area of 4 congruent triangles from the area of the large outside square.
Student Approach #3: Interactive Polypad to Find & Subtract Area
I used the Mathigon Polypad template to find the area of a 16 by 12 rectangle knowing that it covers two corners of the large square.
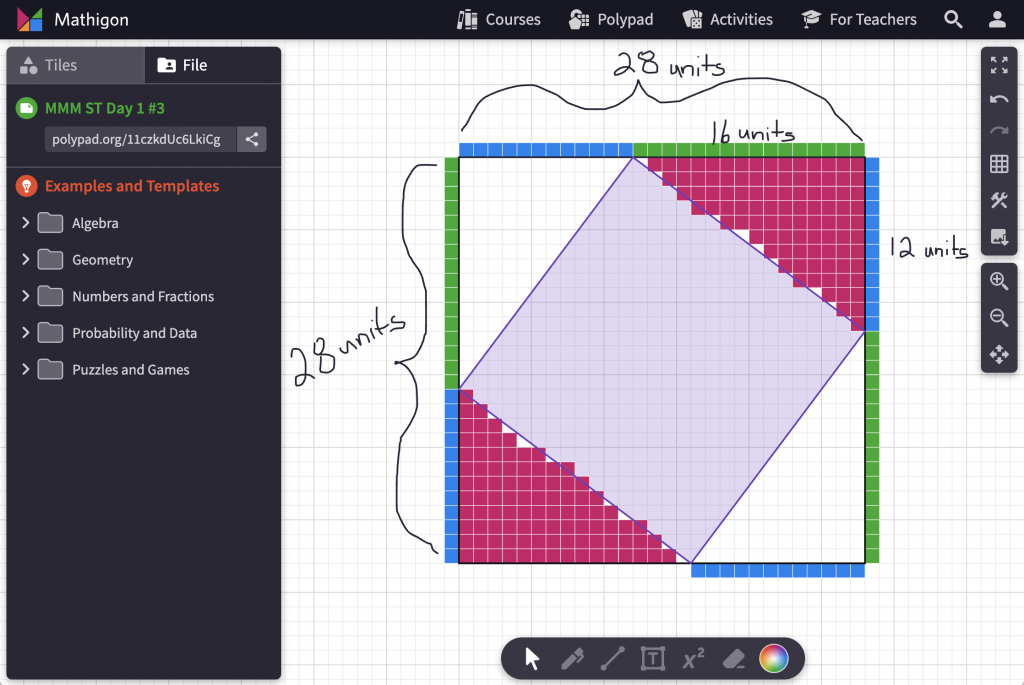
If I double the area of the 16 by 12 rectangle and subtract that from the area of the 28 by 28 square, I’ll be left with the area of the interior square.
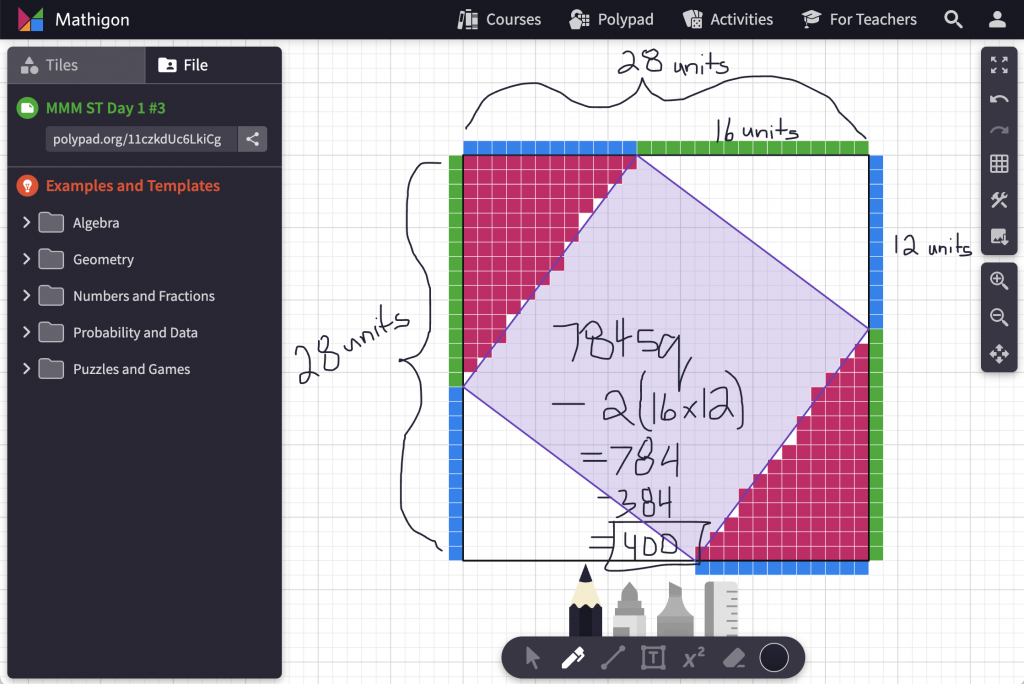
Area of Large Square = 28 units x 28 units = 784 units squared
Area of Two Small Rectangles = 2(16 units x 12 units)
= 2(192 units squared)
= 384 units squared
Subtracting 784 units squared and 384 units squared and I have 400 units squared for the area of the smaller interior square.
Next Moves
Consolidation
Prior to consolidating this task, you might consider giving students the opportunity to more explicitly rearrange the area of the large square into two smaller squares and two rectangles by leveraging this Mathigon Polypad template.
To extend this thinking further, you could have students actually “fill” the interior square with units.
Leverage a few student models to consolidate this task. Consider sequencing them from most accessible to least accessible.
The intent of this lesson is to provide students with an opportunity to bump into the Pythagorean relationship.
Share a new strategy with students that shows them that the area of the inner square is equal to the areas of the squares off the two legs of one of the right triangles.
Here is a short silent solution animation to help visualize this solution.
Generalizing the Pythagorean Relationship
Here is another short silent solution animation to show the Pythagorean Theorem in general.
After you have had an opportunity to make connections between some of the student solutions and the animation, ask your students to complete two more problems that are similar in nature.
Students may want to stick to their method of determining the area of the inner square but encourage them to use the new method of finding the areas off the legs of the right triangle.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
Consolidation Prompt #2:
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!


![Squares To Triangles [Day 1] - 02 - Spark Image](https://learn.makemathmoments.com/wp-content/uploads/2021/06/Squares-To-Triangles-Day-1-02-Spark-Image.jpeg)
![Squares To Triangles [Day 1] - 03 - ESTIMATION IMAGE.001](https://learn.makemathmoments.com/wp-content/uploads/2021/06/Squares-To-Triangles-Day-1-03-ESTIMATION-IMAGE.001.jpeg)
![Squares To Triangles [Day 1] - STRUGGLE Images.001](https://learn.makemathmoments.com/wp-content/uploads/2021/06/Squares-To-Triangles-Day-1-STRUGGLE-Images.001.jpeg)
![Squares To Triangles [Day 1] - STRUGGLE Images 2.002](https://learn.makemathmoments.com/wp-content/uploads/2021/06/Squares-To-Triangles-Day-1-STRUGGLE-Images-2.002.jpeg)
![Squares To Triangles [Day 1] - Student Solution 1-1](https://learn.makemathmoments.com/wp-content/uploads/2021/06/Squares-To-Triangles-Day-1-Student-Solution-1-1-300x225.jpg)
![Squares To Triangles [Day 1] - Student Solution 2-1](https://learn.makemathmoments.com/wp-content/uploads/2021/06/Squares-To-Triangles-Day-1-Student-Solution-2-1-225x300.jpg)
![Squares To Triangles [Day 1] - Student Solution 2-2](https://learn.makemathmoments.com/wp-content/uploads/2021/06/Squares-To-Triangles-Day-1-Student-Solution-2-2--300x273.png)
![Squares To Triangles [Day 1] - Visual Proof Still](https://learn.makemathmoments.com/wp-content/uploads/2021/06/Squares-To-Triangles-Day-1-Visual-Proof-Still.png)
![Squares To Triangles [Day 1] - Consolidation Image Polypad Template](https://learn.makemathmoments.com/wp-content/uploads/2021/11/Squares-To-Triangles-Day-1-Consolidation-Image-Polypad-Template-1024x746.png)
![Squares To Triangles [Day 1] - Consolidation Prompt 1](https://learn.makemathmoments.com/wp-content/uploads/2021/06/Squares-To-Triangles-Day-1-Consolidation-Prompt-1.png)
![Squares To Triangles [Day 1] - Consolidation Prompt 2](https://learn.makemathmoments.com/wp-content/uploads/2021/06/Squares-To-Triangles-Day-1-Consolidation-Prompt-2.png)

