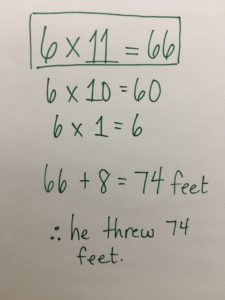SHOT PUT
EQUIVALENCE AND ALGEBRAIC SUBSTITUTION
Student will explore solving equations using the idea of equivalence and substitution.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Extend
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 6 Days
Access each lesson from this unit using the navigation links below
Students will explore solving equations using the idea of equivalence and substitution.
Intentionality…
In this task, students will have an opportunity to reason through an investigation sparked by an athlete throwing shot put. The tasks involve the evaluation of an equation through substitution and the solving of 2-step linear equations. Students will have the opportunity to apply models to reason; in particular, making use of the double number line.
They will also explore big ideas including the following:
- Problems that require multiple calculations can be represented in a single equation.
- Each side of an equation can be thought of as a single unit, where both sides are equivalent.
- Changing the quantity on one side of an equation forces an equivalent change in the other.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the video below showing an athlete throwing a shot put.
Ask students to engage in a notice and wonder protocol. ANYTHING and EVERYTHING that comes to mind is fair game.
Write down all of the student noticing and wondering. For example:
- I notice a stadium.
- I wonder how much the shot put weighs?
- A shot put was thrown.
- That was far.
- How many people are in the audience?
- I wonder how far he threw it?
- And many others…
Take time to acknowledge the noticing and wondering your students have engaged in and try to answer any that you can address right away.
Fuel Sense-making
Walk Through Video
Consider watching the following walk through video that will take you from the start of this task through the consolidation:
Prompt: Setting The Context & Estimating
Then, pose the following question:
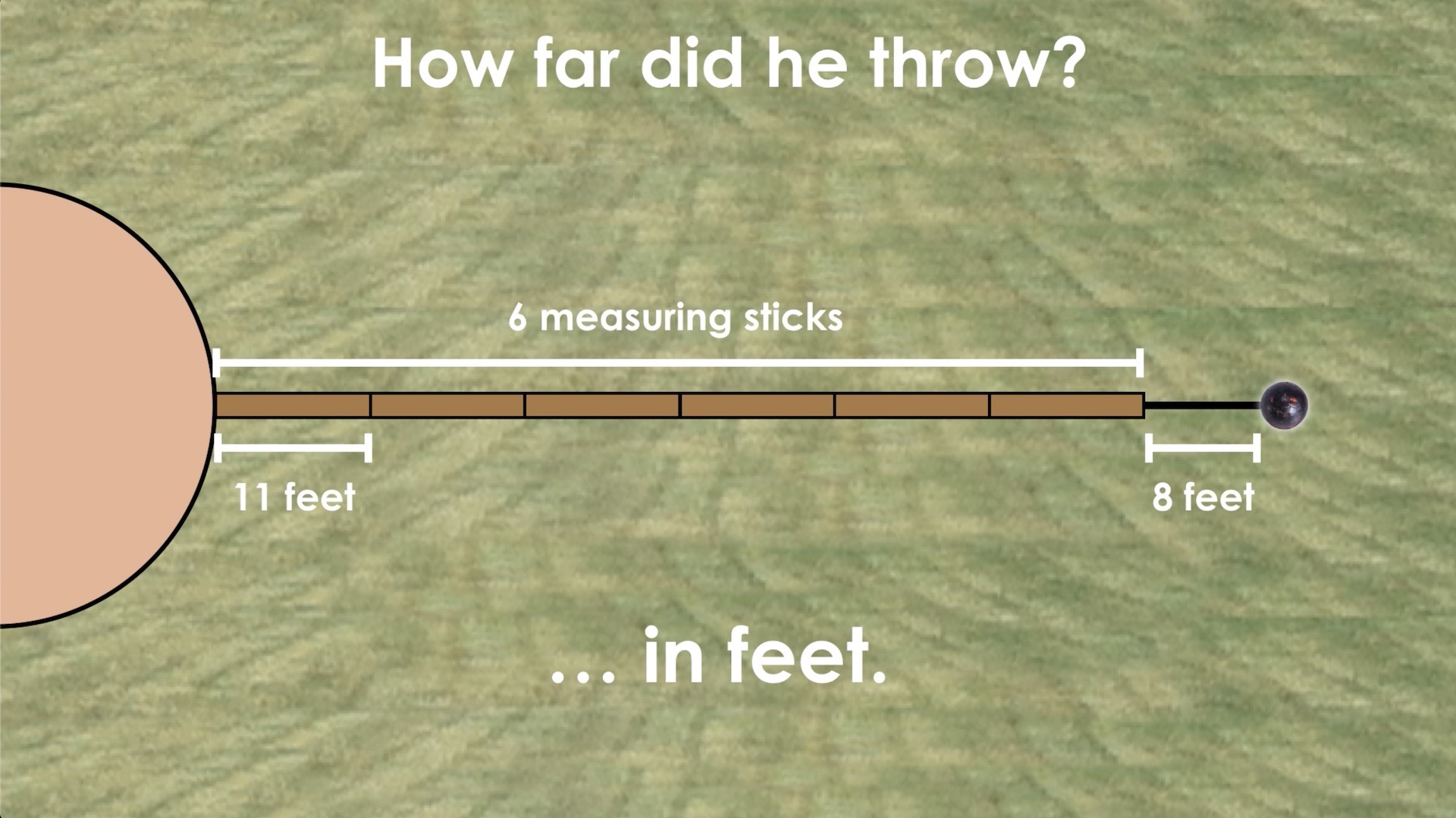
How far did he throw the shot put?
Show students this top-view animation of the shot put stadium and pause when the yellow timer bar appears (or show the image):
Ask students to turn to their peers and make an estimate. Consider asking them to identify a length that is too farand too short to be reasonable prior to making their estimates.
Have students share out their estimates and record them on a number line.
Next, you can continue playing the animation until pausing at the next yellow bar that will appear on the screen (or share the following image) and ask students to improve their estimate using only the brown measuring sticks they see in the visual:
Ask students to use their spatial reasoning to make their estimate and share with their partners.
Crafting A Productive Struggle: Information
When ready, you can resume the animated video or show the following image:
Now, students are ready to be set free to determine the total length of the throw. However, we recommend that you consider mentioning the following as they begin:
How might we convince someone that the total distance you came up with is correct without the use of a calculator?
During Moves
Watch A Lesson In Action
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Bar models.
- Number lines.
- Symbolic representation (i.e.: 6 x 11 + 8 = 11 + 11 + 11 + 11 + 11 + 11 + 8 = 66 + 8 = 74 feet).
- And possibly others.
Have students share their strategies and reasoning for determining the the total number of feet to measure the distance.
Ask them to convince you and their peers that their answer is correct by sharing mathematical models.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Facilitator Notes
Keep in mind that prior to students being given the length of each brown measuring stick, students are forced to use algebraic thinking where they know:
6 iterations of the brown measuring stick plus 8 additional feet is equivalent to the length of the shot put throw.
Symbolically, this can be written as:
6b + 8 = l
where b represents the length of each measuring stick (or rate) and and l represents the total length of the shot put throw.
Student Approaches
Student Approach #1: Number Line & Counting
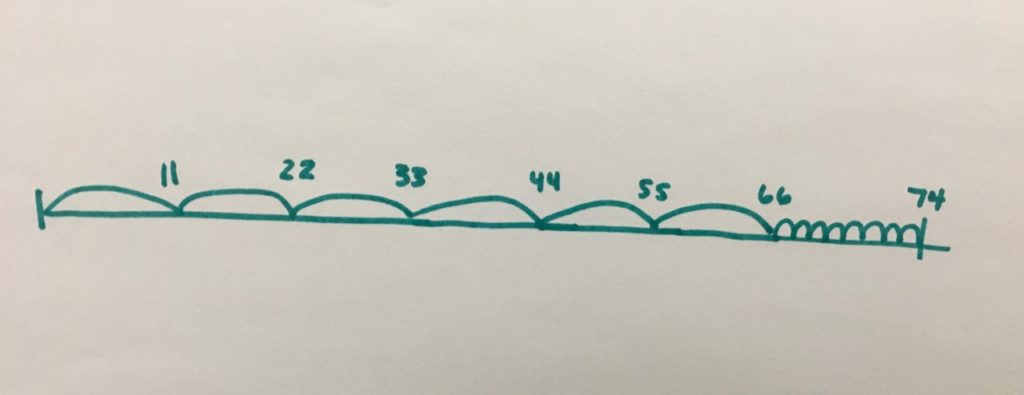
I drew a number line. I know that each measuring stick is 11 feet, so I started counting by 11 six times. To count by 11, I added 10, plus one more. So 11 + 10 = 21, 21+ 1 = 22, and so on. After I counted 11 six times, I just added 8 more feet by counting on, 67, 68, 69…..
Approach
This student used a number line to access this task through counting.
Student Approach #2: Partial Products
I multiplied 6 by 11, because there are 6 measuring sticks that are 11 feet long. To multiply 6 x 11, I did 6 x 10 + 6 x 1. Once I had 66 feet for the 6 measuring sticks, I added 8 more feet. I know that 66 + 4 is 70, so 4 more is 74.
Approach
This student accesses this task through multiplication and addition in a multi-step solution. They used partial products resulting from the distributive property of multiplication over addition to multiply 6 x 11. For the addition, the student decomposed the addend in order to make a friendly number.
Student Approach #3: Symbolic Equation
I wrote the situation as an equation. 6 groups of 11 + 8 = 74. I know that the answer is 74 because 6 x 11 is 66, plus another 8 feet is 74 feet total.
Approach
This student understands that the shot put situation, (although requiring more than one operation) can be presented as a single equation. They used mental math and automaticity to determine the equivalence in total number of feet.
Next Moves
Reveal
After consolidating learning using student generated solution strategies and by extending their thinking intentionally, we can share what really happened by showing the following to reveal how far the shot put was thrown.
Alternatively or in addition to the video, you can show the still image below.
Answer: 74 feet.
Revisit the student answers.
Consolidation
During the consolidation, use student generated solution approaches and strategies to facilitate a discussion intended to connect student approaches which may involve separate calculations into a single equation.
For example, in Student Approach #2, the student first multiplied 6 sticks x 11 feet per stick using partial products to reveal a total of 66 feet. Then, the student added the additional 8 feet in a separate step and/or equation:
6 x 11 = 6 x 10 + 6 x 1 = 60 + 6 = 66
66 + 8 = 74
Help students see how this approach can be represented in a single equation.
6 x 11 + 8 = 74
or
6(11) + 8 = 74
This is an important step in nudging students towards constructing an understanding of equations involving unknown values.
For example, in this particular problem, we were working with this equation:
6x + 8 = l
where x represents the length of each measuring stick and l represents the length of the shot put throw.
Since we are then given x = 11 feet, students can substitute 11 feet for x:
6(11 feet) + 8 feet = l
66 feet + 8 feet = l
74 feet = l
You might find the following animation and visual helpful as you prepare for this consolidation or even potentially use during the consolidation:
Extend
Walk Through Video
Extension Prompt & Intentionality
Show the following animation video:
Be sure to pause the video when you see the yellow timer bar appear at the bottom of the screen to give students an opportunity to estimate.

Give students an opportunity to first estimate using their spatial reasoning skills before they share their estimates and then resume the animation video or share the following image:
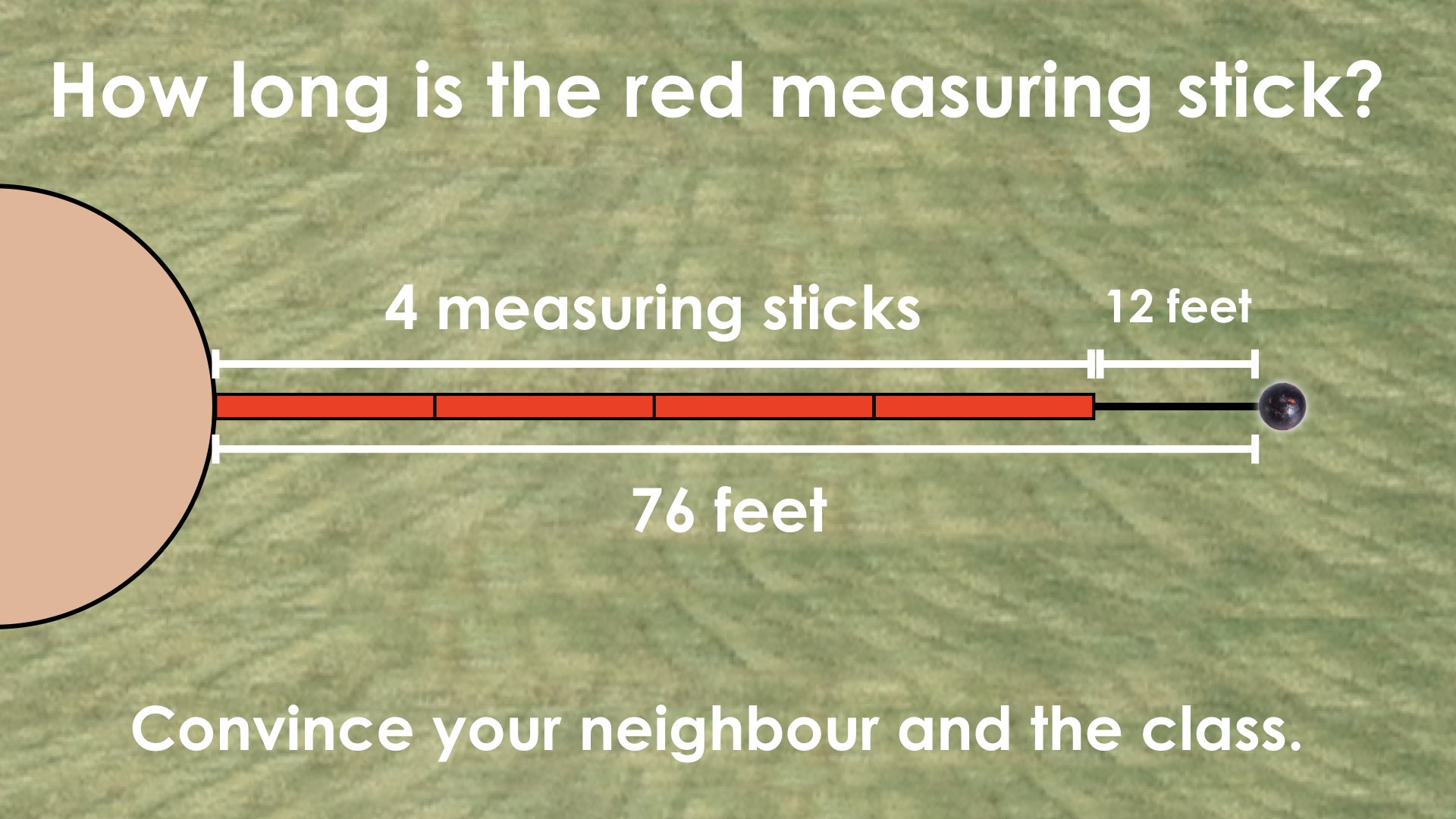
Consider verbally reiterating the EXTEND: PROMPT context:
On the second throw, the shot put landed at the 76 foot marker. The officials used 4 measuring sticks and had to pace out 12 extra feet to measure the total distance.
How long were the measuring sticks?
Allow students time to reason through this task and ensure that they are being prompted to convince their math community of their approach and strategy.
Intentionality:
This task can be used to investigate a situation creating the need for a two-step linear equation.
As students work, encourage them to consider using a number line to represent their thinking.
Student Approach #1:
I drew a number line to represent the situation. I know that there were 4 red measuring sticks (those are the jumps) and then 12 more feet, and that was equal to 76 feet altogether. I started by backing up 12 feet, so I did 76 -10 is 66, and minus 2 more is 64. Then I knew I had to divide the 64 feet into 4 parts because there are 4 sticks. I decided to first divide into 2 sticks, that’s 32 feet. And then I divided that stick in half to make 4 parts, so each stick is 16 feet.
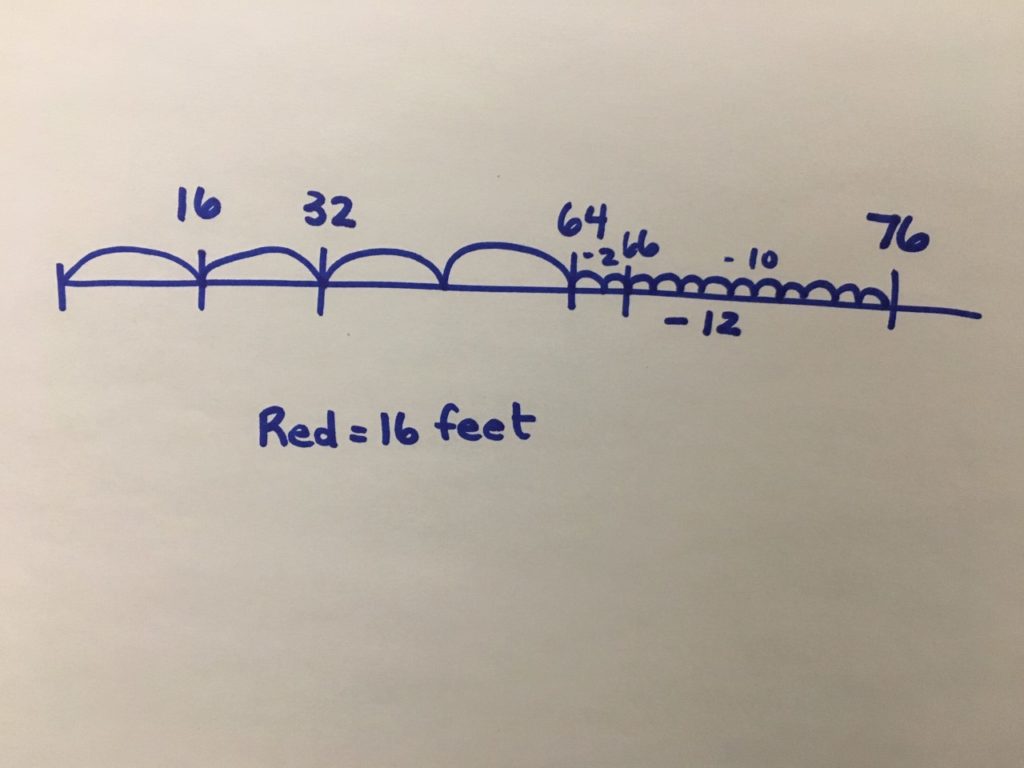
Approach:
This student used the number line to model the situation. The student decided to remove the 12 feet, and then divide the 64 remaining feet in half, and then half again to create 4 equal parts. The division that was used is partitive. They had 64 feet and a known number of sticks, the length of each stick was unknown.
Student Approach #2:
I know that the throw was 76 feet in total. I also know that the official had to add 12 feet after the 4 measuring sticks, so I started by subtracting the 12 feet. Now I know that the 4 red measuring sticks measured a total of 64 feet. I have to divide 64 by 4. So I drew 64 circles and I know I have to share them amongst the 4 sticks. I started by giving every stick 1 foot. Then I saw that I could give every stick ten more feet. But there weren’t enough feet left to give another 10, but I could give each stick another 5. So 1 foot + 10 feet + 5 feet equals 16 feet for each measuring stick.
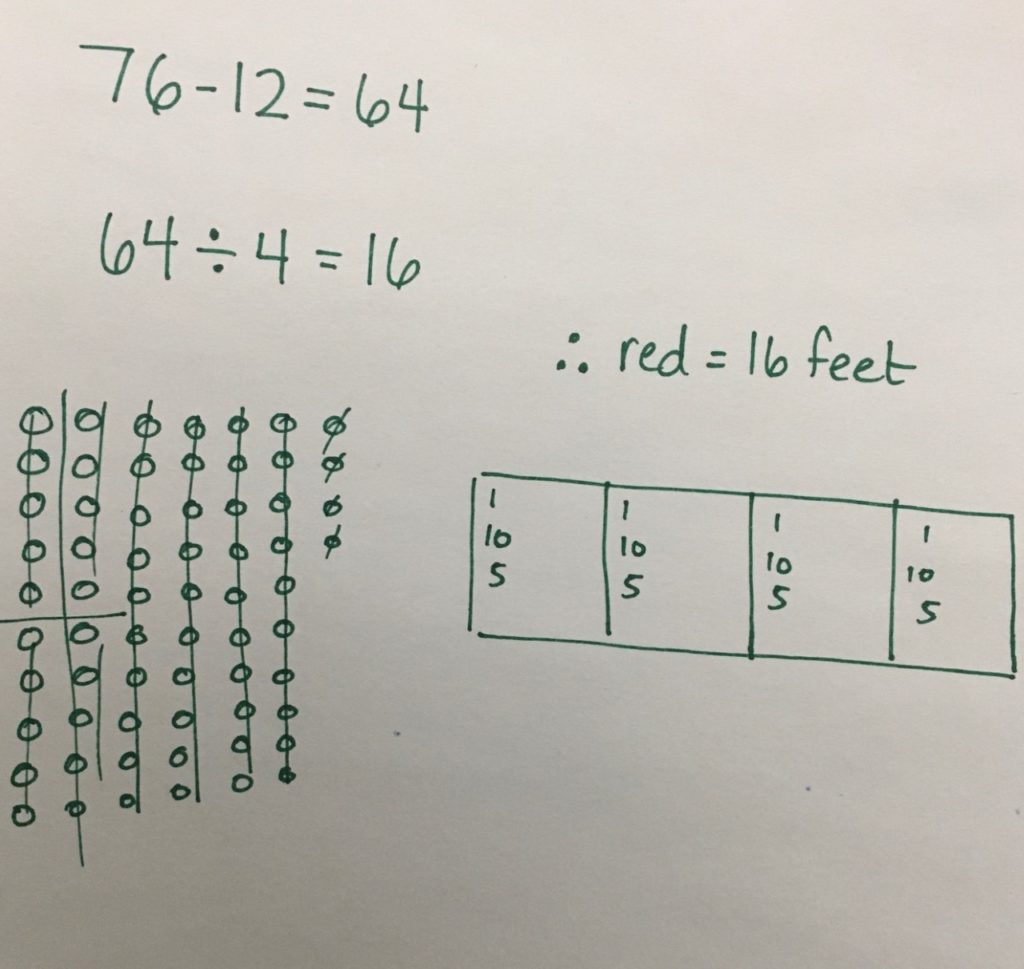
Approach:
This student solved the problem symbolically and used a pictorial set model to perform the partitive division step by distributing the 64 feet amongst the 4 parts (or measuring sticks).
Student Approach #3:
I know that this situation can be represented by an equation with one unknown variable. The unknown quantity is the length of the red stick. Once I had the equation written, I tried to isolate r (the length of the red stick). I started by subtracting 12 feet from both sides. Then I had 4r = 64. I know that if 4r = 64, then 2r = 32, because that’s half. And when I half again, I find out the length of one red stick, 16 feet.
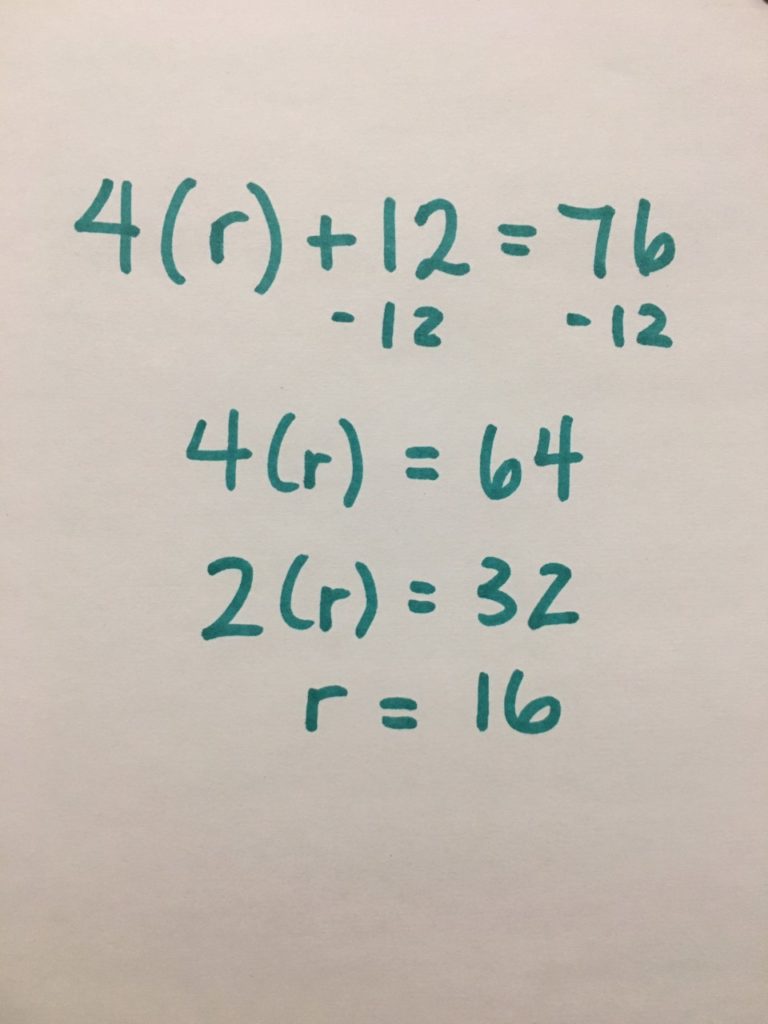
Approach:
This student used a symbolic representation of the situation by writing an equation. Their strategy was to isolate r (the length of red). The algebraic thinking used here is a symbolic representation of the strategy shared on the number line in student approach #1.
NEXT MOVES
Consolidate:
Consolidate learning using student generated solution strategies based on what you selected and how you sequenced while monitoring during the Sense Making portion of the lesson.
The purpose of the consolidation is to make connections between strategies and reveal and/or solidify big ideas.
In particular, engage students in a discussion about the double number line and how it can be used to show equivalence and reveal unknown quantities in a single variable equation.
For example, in Throw #2, the equation 4r + 12 = 76 reveals to us two equivalent units; 4r + 12 which is also equivalent to 76 feet.
Students may have used this relationship on the number line to isolate the 4r (or 4 red sticks) by subtracting 12 feet from 76 feet.
This reveals a new equality statement: that the length of 4 red sticks is equivalent to 64 feet, or algebraically as 4r = 64.
If one or more students solve Throw #2 using an algebraic equation only, ensure that you reveal how this symbolic approach can be modelled on the double number line. Utilizing student generated solution strategies to engage in this discussion is optimal.
Reveal:
After consolidating learning using student generated solution approaches and strategies based on what you selected and how you sequenced, share the following:
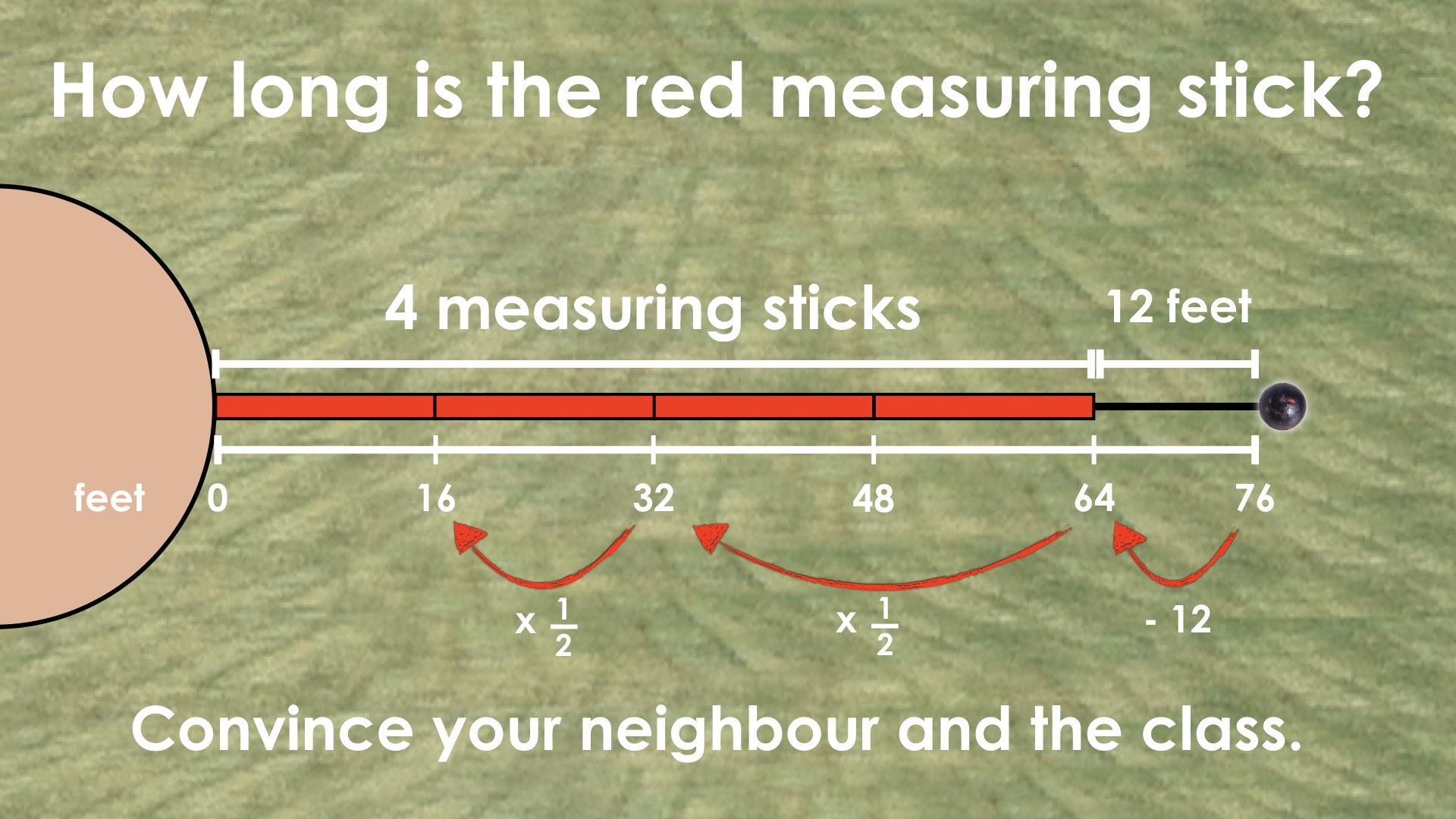
ANSWER: The length of the red measuring stick is 16 feet.
You may also consider explicitly connecting the visual representation on the number line to the symbolic representation:
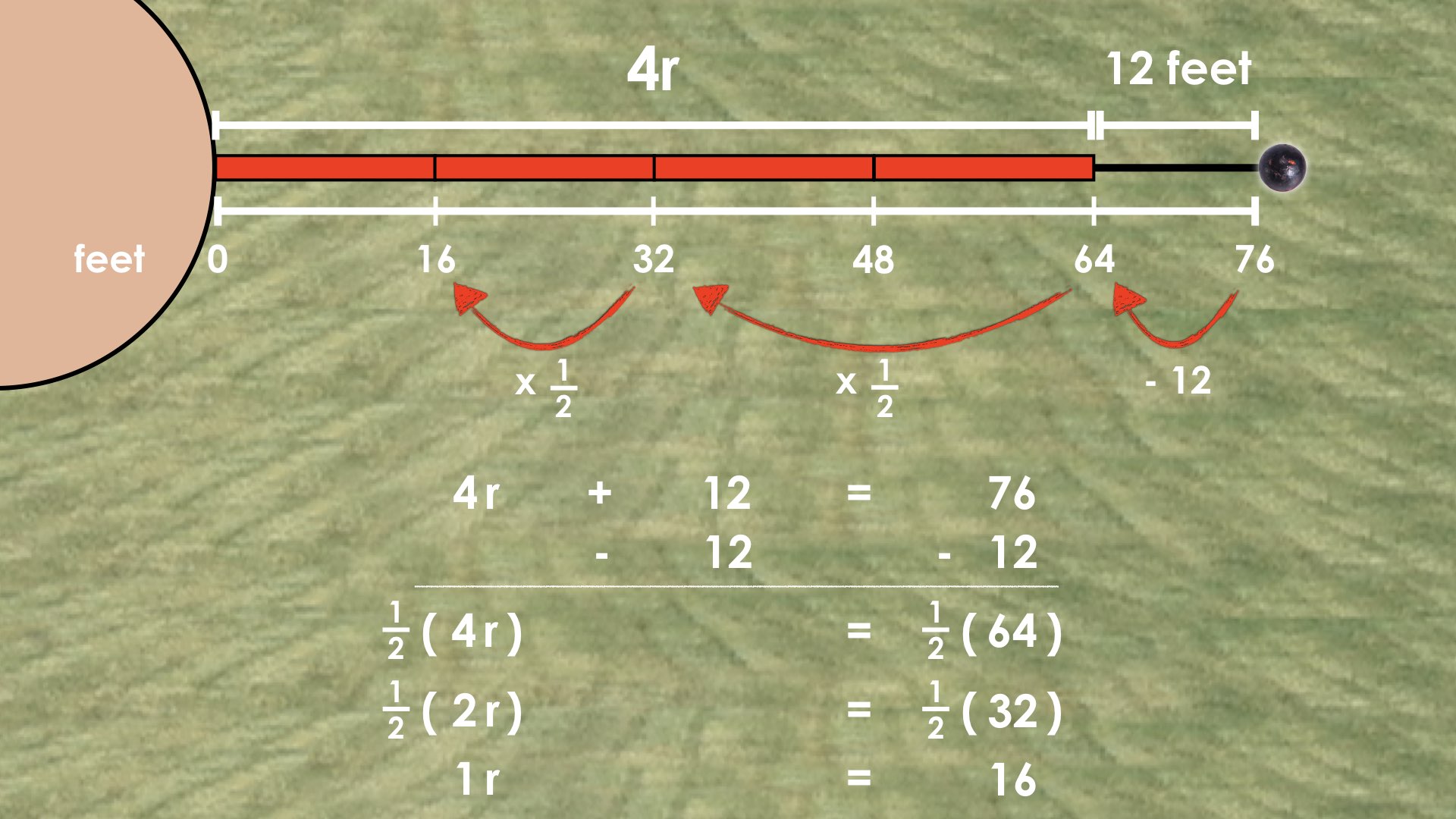
Reflect:
Provide students an opportunity to reflect on their learning by offering this consolidation prompt to be completed independently.
Consolidation Prompt:
There were two additional throws that were measured with different measuring sticks.
On the first throw, the officials used 11 purple measuring sticks and paced out an additional 4 feet to measure a total throw length of 70 feet.
On the second throw, the officials used 7 blue measuring sticks, but they went 8 feet past the shot put landing spot.
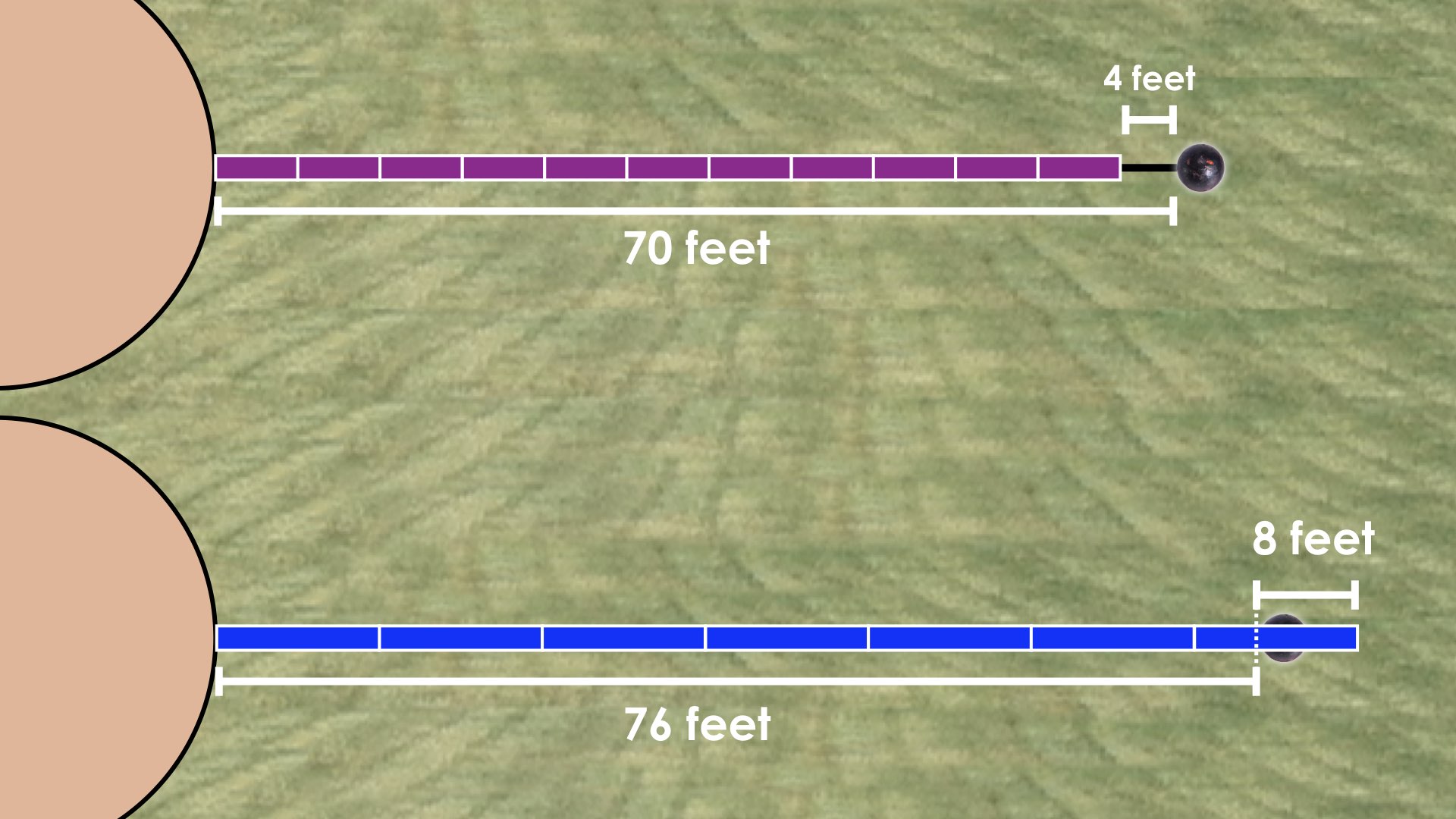
Determine the length of the purple and blue measuring sticks using the approach you’re most comfortable with.
If you used a concrete and/or visual approach, attempt to represent your thinking symbolically by creating an equation and solving for the length of each measuring stick.
If you used a symbolic approach (i.e.: creating an equation), attempt to represent your thinking concretely or visually to demonstrate your understanding of why the steps you took to solve the equation worked.
Facilitator Note:
The reason for providing students with the direction to solve in two ways is to encourage them to use a method they are most comfortable with, while also pushing them to consider trying a different approach and/or strategy like utilizing the double number line.
If students are successful solving for the length of the measuring stick for Throw #3, but unsuccessful solving for the length of the measuring stick for Throw #4, this might be due to the fact that using 7 blue measuring sticks will extend beyond 76 feet and we must adjust by removing 8 feet to compensate.
Answers: Purple = 6 feet; Blue = 12 feet.
Symbolic Representation (Equation) for Throw #3: 11p + 4 = 70
Symbolic Representation (Equation) for Throw #4: 7b – 8 = 76
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt:
There were two additional throws that were measured with different measuring sticks.
On the first throw, the officials used 11 purple measuring sticks and paced out an additional 4 feet to measure a total throw length of 70 feet.
On the second throw, the officials used 7 blue measuring sticks, but they went 8 feet past the shot put landing spot.
Determine the length of the purple and blue measuring sticks using the approach you’re most comfortable with.
If you used a concrete and/or visual approach, attempt to represent your thinking symbolically by creating an equation and solving for the length of each measuring stick.
If you used a symbolic approach (i.e.: creating an equation), attempt to represent your thinking concretely or visually to demonstrate your understanding of why the steps you took to solve the equation worked.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Facilitator Note:
The reason for providing students with the direction to solve in two ways is to encourage them to use a method they are most comfortable with, while also pushing them to consider trying a different approach and/or strategy like utilizing the double number line.
If students are successful solving for the length of the measuring stick for Throw #3, but unsuccessful solving for the length of the measuring stick for Throw #4, this might be due to the fact that using 7 blue measuring sticks will extend beyond 76 feet and we must adjust by removing 8 feet to compensate.
Answers: Purple = 6 feet; Blue = 12 feet.
Symbolic Representation (Equation) for Throw #3: 11p + 4 = 70
Symbolic Representation (Equation) for Throw #4: 7b – 8 = 76
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!