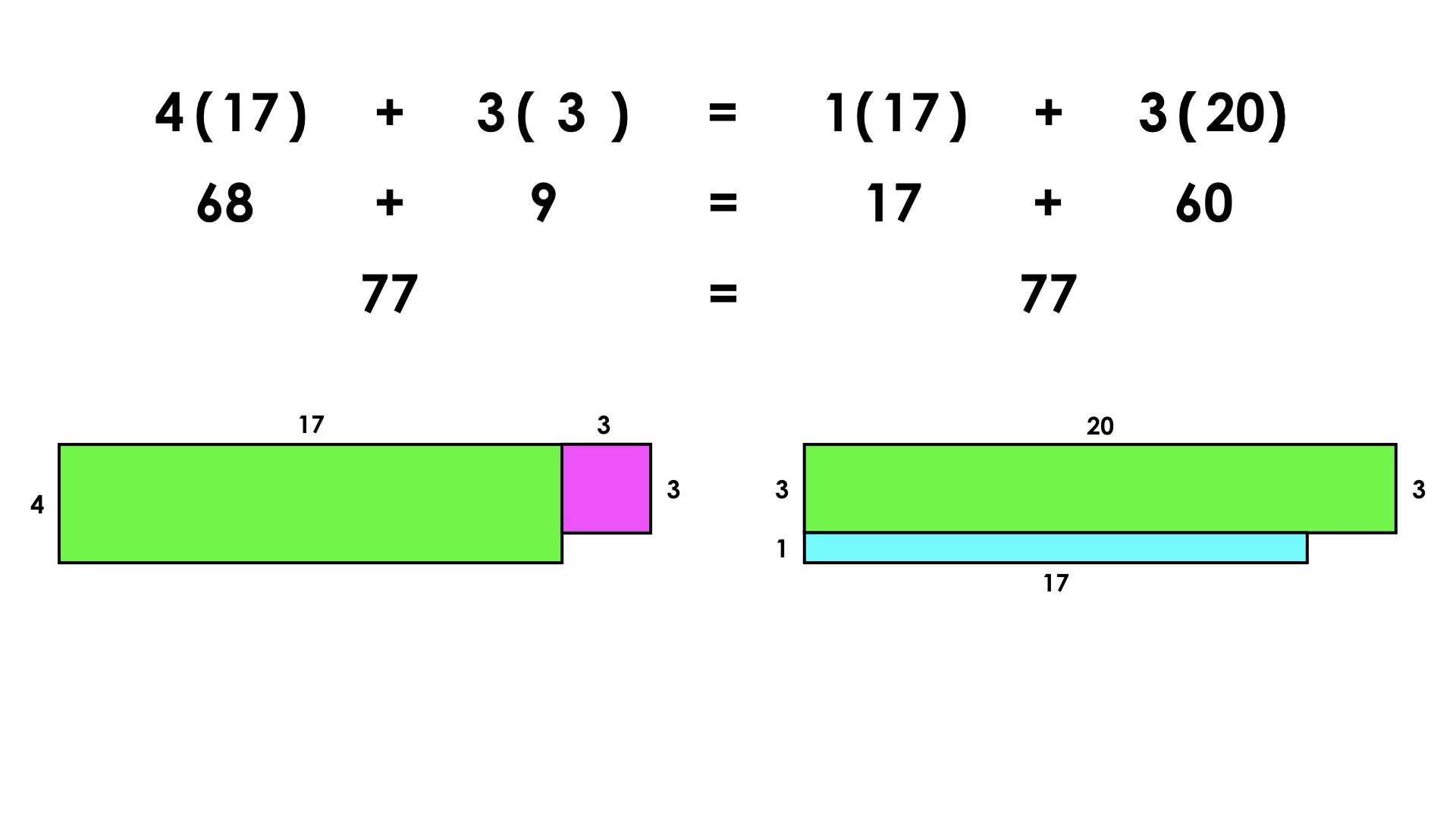SHOT PUT [DAY 5]
EQUIVALENCE AND ALGEBRAIC SUBSTITUTION
Student will explore solving equations using the idea of equivalence and substitution.
Intentionality
Math Talk
Spark Curiosity
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 6 Days
Access each lesson from this unit using the navigation links below
Students will explore solving equations using the idea of equivalence and substitution.
Intentionality…
Today, students will have an opportunity to reason through an investigation extending the shot put context. Again, the tasks involve measuring different shot put throws with two different length measuring sticks. However, in this scenario, the total length of each throw and length of each measuring stick is known, but the number of measuring sticks is unknown allows students to solve a two-variable system of linear equations using mathematical models such as the number line and/or double number line.
This scenario builds off of our day 2 understanding of quotative division meaning the length of each stick (i.e.: rate or quota) is known and the number of sticks (i.e.: parts) is unknown. Recall from yesterday that we were trying to determine the length of each measuring stick, whereas today we will be trying to find the number of sticks instead. Again, although we are not necessarily using quotative division, the big ideas are still prevalent.
They will also explore big ideas including the following:
- There are two types of division; partitive and quotative.
- Each side of an equation can be thought of as a single unit, where both sides are equivalent.
- Quantities can be reassociated to create new units that can be substituted for equivalent quantities.
- A multiple of one quantity can be equivalent to a multiple of another quantity which can be used to substitute.
- The algebraic strategy of substitution can assist in solving for unknown quantities in an equation.
Math Talk
In this string of related problems, we will be providing students with 3 visuals of arrays and area models that will promote the idea of reassociating units to create more friendly factors.
As you work through this math talk, ask students the different ways they might go about determining the total quantity in the arrays or area model.
Image #1:
Image #2:
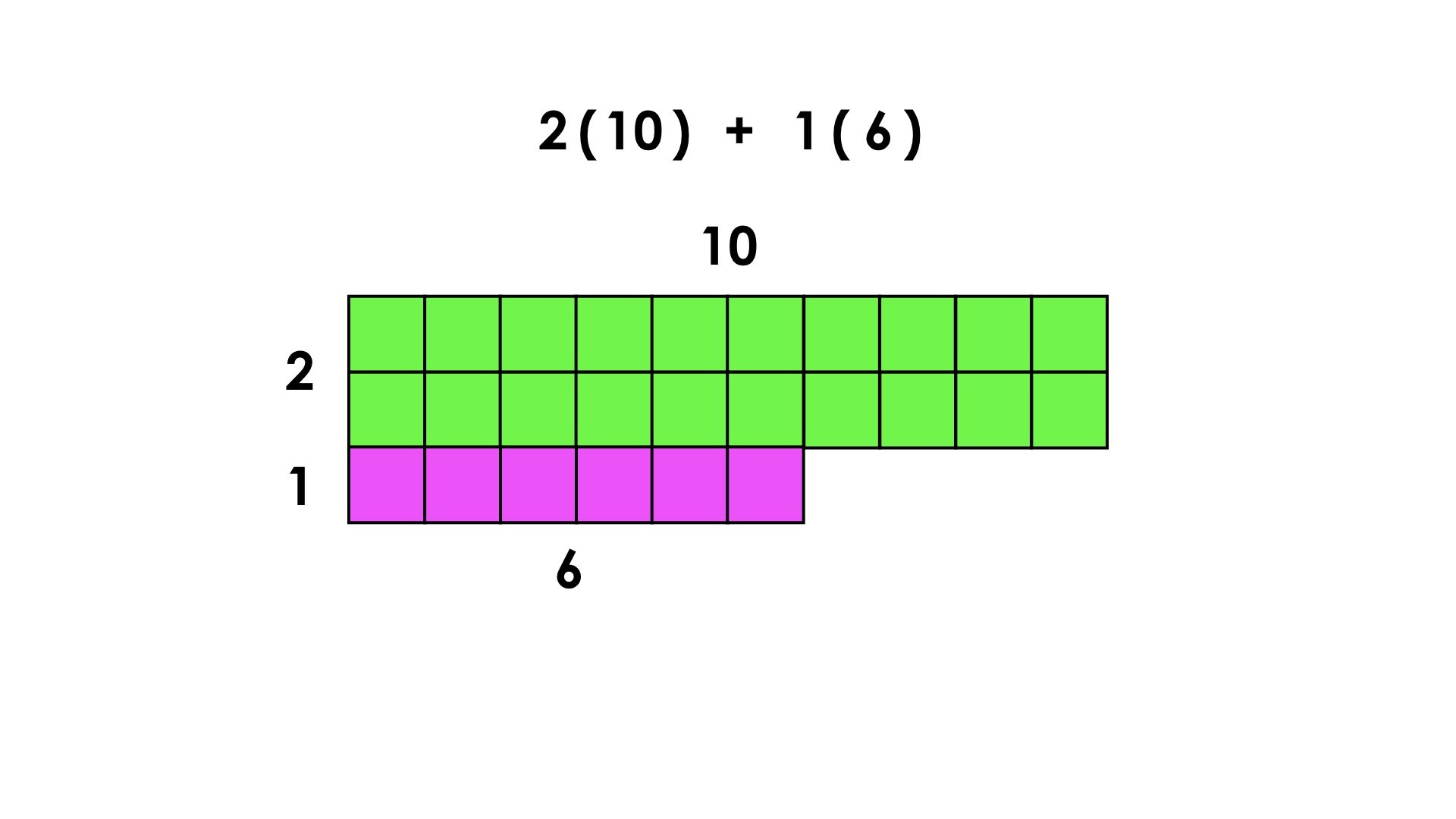
Image #3:
Image #4:
Consider modelling student thinking on an area model in order to elicit the big idea of the associative property of multiplication.
Walk Through Video
If you’d like to see how you might model a portion of this math talk, consider viewing this walk-through video.
Facilitator Notes
This idea is important in this unit as we utilize the idea of the associative property to help us emerge the algebraic strategy of substitution.
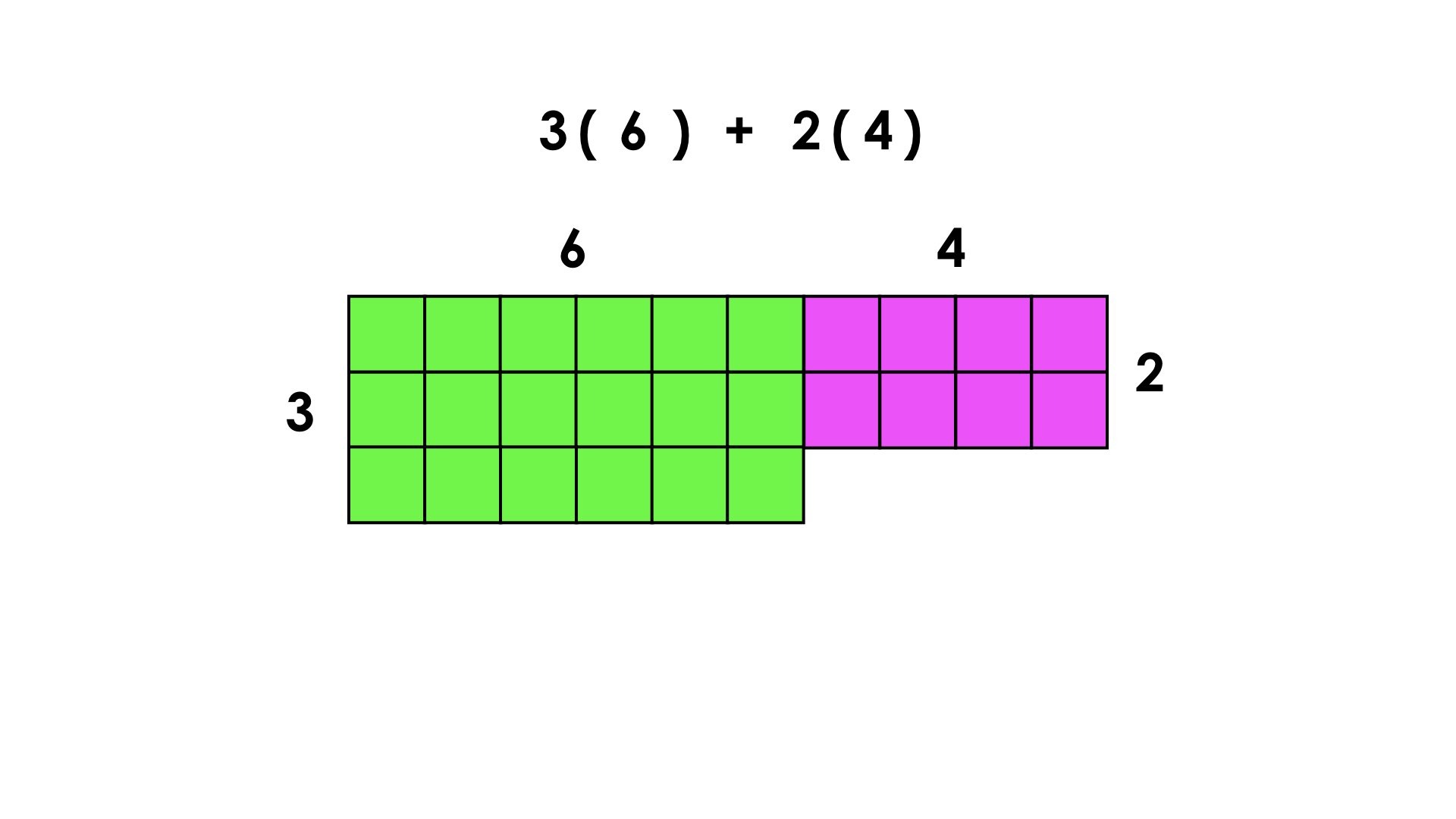
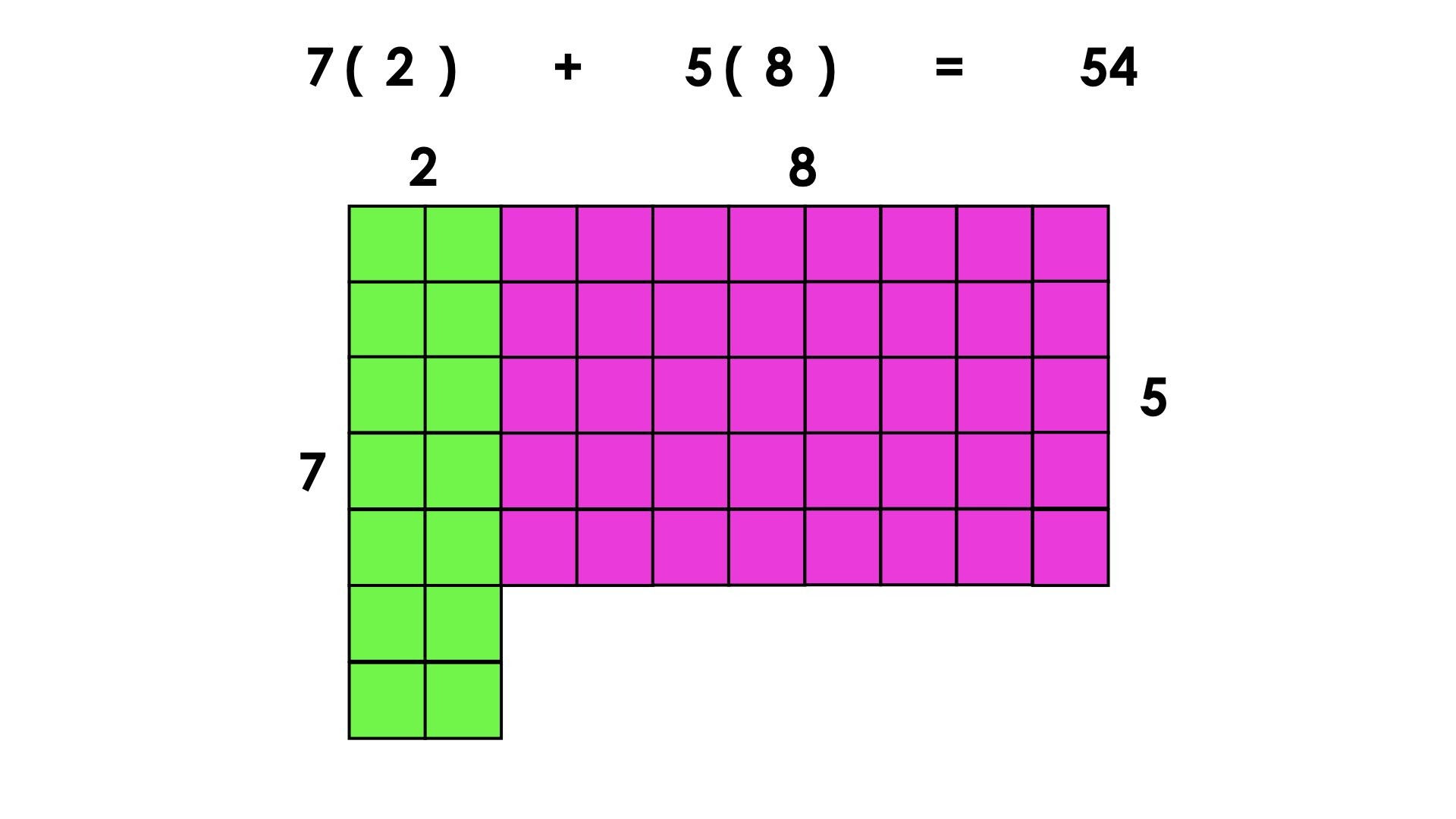
When thinking of the first pair of arrays from the string, we can represent this total quantity as:
3(6) + 2(4)
Which is equivalent to:
(6 + 6 + 6) + (4 + 4)
By commuting and reassociating each quantity of 4 with a quantity of 6, this new unit of 6 + 4 is equivalent to a unit of 10.
6 + (6 + 4) + (6 + 4)
or
6 + 10 + 10
or
6 + 2(10)
The intent of this string is to help uncover the associative property of multiplication as well as the idea of substitution as a means to build number fluency and flexibility while also developing our understanding and skills to support algebraic thinking.
In each of the math talk visuals, the hope is that students will be able to recognize that they can look at the sum of two arrays (or sum of two pairs of factors) in more than one way.
For example in image #2, connecting both arrays together and viewing as a tall and thin array and a shorter and longer array yields the following equation:
Whereas partitioning into a longer, larger array of 10 groups of 5 would create an equal equation that might be easier for us to compute using mental math skills:
Something similar happens with image #3:
The goal is that a student could look at any expression involving the sum of two multiplication terms and give students the flexibility to use the associative property to their advantage.
Sense Making
Crafting The Productive Struggle: Prompt #1
Pose the following question:
After a shot put was thrown, one official measured the distance with precisely 5 teal measuring sticks plus an additional 11 feet, while a second official measured the distance precisely with 6 teal measuring sticks plus 1 additional foot.
a) How long is the teal measuring stick?
b) How long was the shot put throw?
Walk Through Video
If you’d like to see how you might model a portion of this math talk, consider viewing this walk-through video.
Facilitator Notes
Students are strongly encouraged to model this scenario using a double number line. By doing so, students may be able to visually see the unknown length of a measuring stick by using the measurement from one of the officials and comparing against the measurement from the other official.
In particular,
The double number line allows for students to solve for the unknown quantity (length of a teal measuring stick) through investigation while leaving the facilitator with an opportunity to connect the visual representation to the algebraic procedure of solving through simplifying and isolating the variable.
Crafting The Productive Struggle: Prompt #2
Next, pose this question:
After a shot put was thrown, one official measured the distance with precisely 5 beige measuring sticks plus an additional 10 feet, while a second official measured the distance precisely with 6 beige measuring sticks but had to pace back 3 feet.
a) How long is the beige measuring stick?
b) How long was the shot put throw?
If students solve the length of the measuring sticks using a visual and/or pictorial representation, encourage them to represent their thinking symbolically, and vice versa.
During Moves
While Students Are Productively Struggling…
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Student Approaches
Prompt #1 Sample Student Approaches
Student Approach #1: Number Line Using Reasoning
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Student Approach #2: Pictorial Equation Using Elimination
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Student Approach #3: Symbolic Equation Using Elimination
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Prompt #2 Sample Student Approaches
Student Approach #1: Number Line Using Reasoning
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Student Approach #2: Pictorial Equation Using Elimination
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Student Approach #3: Symbolic Equation Using Elimination
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Next Moves
Reveal
After consolidating learning using student generated solution strategies and by extending their thinking intentionally, we can share what really happened by showing the following video/image revealing the length of the teal measuring stick and length of the throw.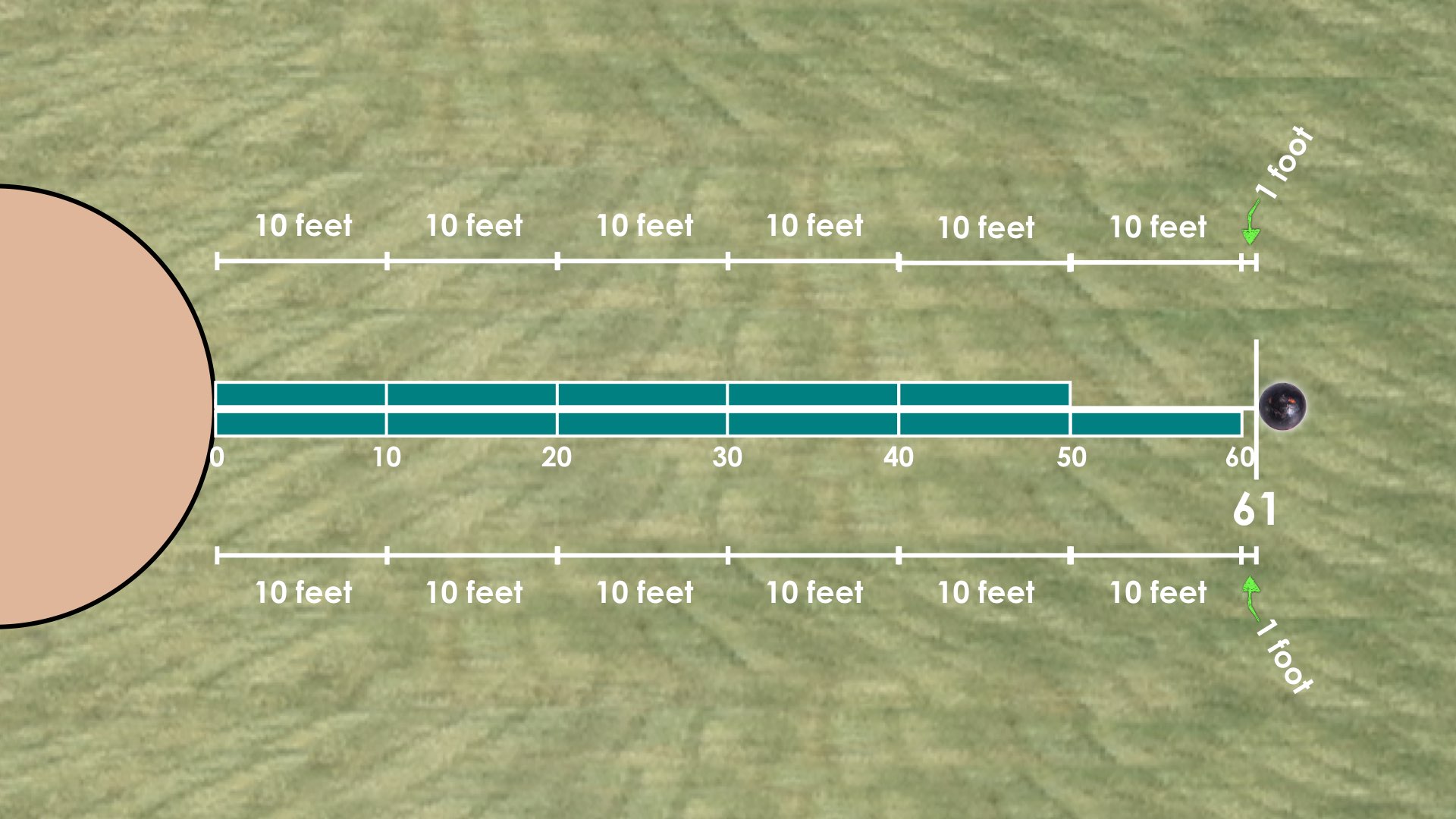 Answers: Teal Measuring Stick = 10 feet; Length of Throw = 61 feet.
Revisit the student answers.
Answers: Teal Measuring Stick = 10 feet; Length of Throw = 61 feet.
Revisit the student answers. Consolidation
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering this consolidation prompt to be completed independently.
Consolidation Prompt #1:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Consolidation Prompt #2:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Facilitator Notes
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Resources & Downloads
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!