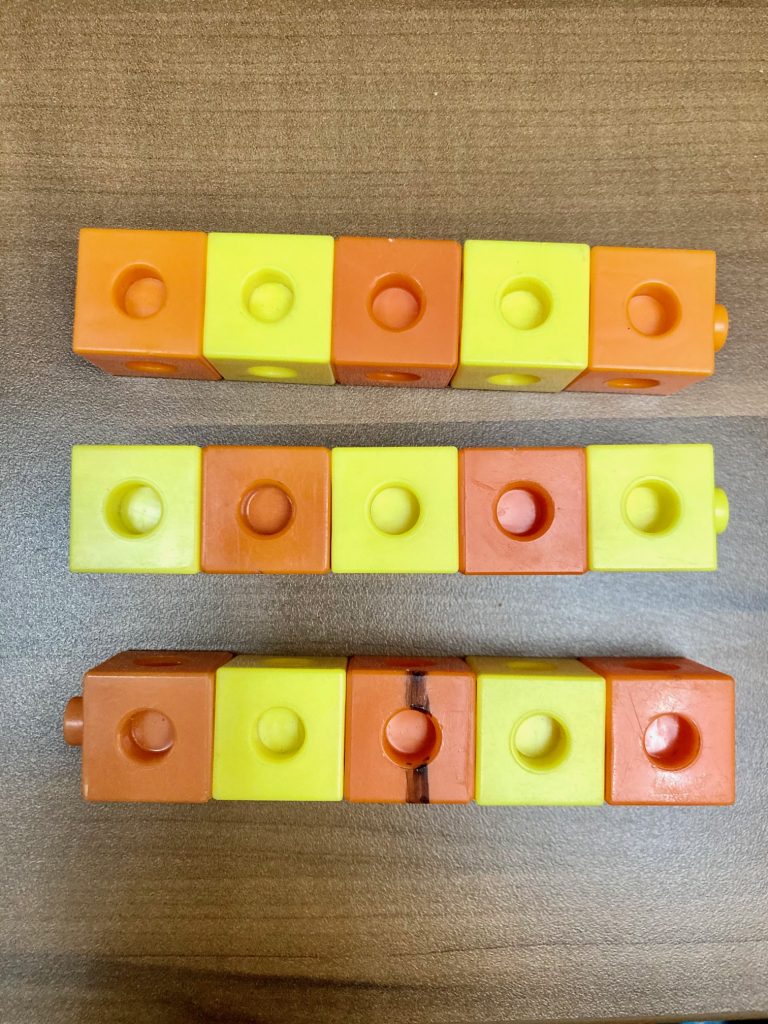PIZZA PARTY
DIVIDING FRACTIONS THROUGH QUOTATIVE DIVISION
Explore quotative division of fractions conceptually using the bar model, double number line and ratio table.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will determine the number of servings of pizza in two and a half pizzas if each serving is one-fifth pizza per person.
In this task, students will observe servings of pizza being dished out onto a plate. Each person will receive one-fifth of a pizza. This quantity of pizza is considered one serving. If the party host has two and one-half pizzas left, how many servings can they make? In this context, students are dividing two and one-half pizzas by one-fifth pizza/person, this is a context that elicits quotative division.
The purpose is to reveal the number of iterations or parts of the rate (one-fifth pizza/person) in the other quantity of the same unit (two and one-half pizzas). Some of the big ideas that may emerge through this task include:
- There are two types of division;
- In quotative division, both the dividend and the divisor have the same unit (pizza and pizza).
- The divisor is a rate.
- The quotient can represent the number of parts or iterations of the rate.
- Quotative division can be accessed through skip counting, repeated addition, repeated subtraction or multiplication.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Replaying the video and/or leaving a screenshot from the video up can be helpful here.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group. Be sure to write down these noticings and wonderings on the blackboard/whiteboard, chart paper, or some other means to ensure students know that their voice is acknowledged and appreciated.
Some of the noticing and wondering that may come up includes:
- There is a pizza.
- It looks like a homemade pizza.
- I wonder what brand of frozen pizza that is?
- It is burnt on some of the edges.
- I wonder how many people are going to be eating?
- The person only cut one part of the whole pizza.
- I wonder what fraction of the whole pizza that is?
- I think they are going to cut it into 6 equal strips.
- I wonder how long it took to cook?
At this point, you can answer any wonders that you can cross off the list right away and of course, you can create your own answers for some of these wonders. For example:
- You could explain that this is a specific brand of frozen pizza that you and your own family enjoy.
- You could share that while your family has ___ people in it, this pizza was being served at a birthday party.
- You could share that it took about 24 minutes to cook.
- And so on…
Estimation: Prompt
After we have heard students and demonstrated that we value their voice, we can land on the first question we will challenge them with:
What fraction of the pizza was sliced?
We can now ask students to make an estimate (not a guess) as we want them to be as strategic as they can possibly be. This will force them to determine a fraction of the pizza that would be reasonable before determining a more precise answer. Consider asking students to think about an estimate that would be “too low” and an estimate that would be “too high” before asking for their best estimate in order to help them come up with a more reasonable estimate.
It can be helpful to encourage students to draw a model of their thinking by creating a rectangle and partitioning the pizza to show the fraction of pizza that was sliced.
Encourage students to share their estimates, however avoid sharing their justification just yet. We do not want to rob other students of their thinking.
Facilitator Note:
You might consider intentionally omitting the word “fraction” from the prompt if you’d like to keep the initial conversation more open. By doing so, you might hear students describing the amount of pizza using fractional language, decimal language or standard units of measure. All descriptions of the amount are welcome. This could be a great opportunity to discuss equivalence.
Estimation: Reveal
Show students the following image:
Students can now see that the first slice that was cut in the spark video represented approximately 1 fifth of the pizza.
Fuel Sense-making
Crafting A Productive Struggle:
Show students this short silent animation clip to reveal how many pizzas are left to be sliced and served.
Prompt students by stating:
If the host intends to serve each guest at the party one-fifth of a pizza, how many servings can be made with the remaining two and one-half pizzas?
During Moves
While Students Are Productively Struggling….
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Concrete materials.
- Paper folding.
- Using an area model.
- Using a bar model.
- Using equivalence.
- Using a symbolic representation.
Have students share their strategies and reasoning for how to determine servings of one-fifth pizza per person in two and one-half pizzas. Ask them to convince you and their peers that their answer is correct by sharing mathematical models.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
Student Approach #1: Linking cubes and Skip Counting
I made three pizzas out of linking cubes. I made each pizza out of 5 cubes because they are sliced into 5 pieces. In two pizzas, there are 10 servings. In the last pizza there is not a whole busy, only have. I can see two whole slices, and there is not enough to make another slice. They can slice 12 servings of pizza.
Student Approach #2: Paper Folding & Skip Counting
I cut three strips of paper. I folded each strip into five parts. I know that every part is one serving. I started to count the parts, I was able to count 12 and one-half parts in two and one half pizzas.
Student Approach #3: Symbolic using Decomposition
I know that there are 5 servings in each pizza. So I decomposed the two and one half into one pizza, one pizza and one-half pizza. Each whole pizza is 5 servings. If one whole pizza is 5 servings, then a half pizza is half of 5, so it is 2 and one-half servings.
Next Moves
Consolidation
Leverage a few student models to consolidate this task. Consider sequencing them from most accessible to least accessible.
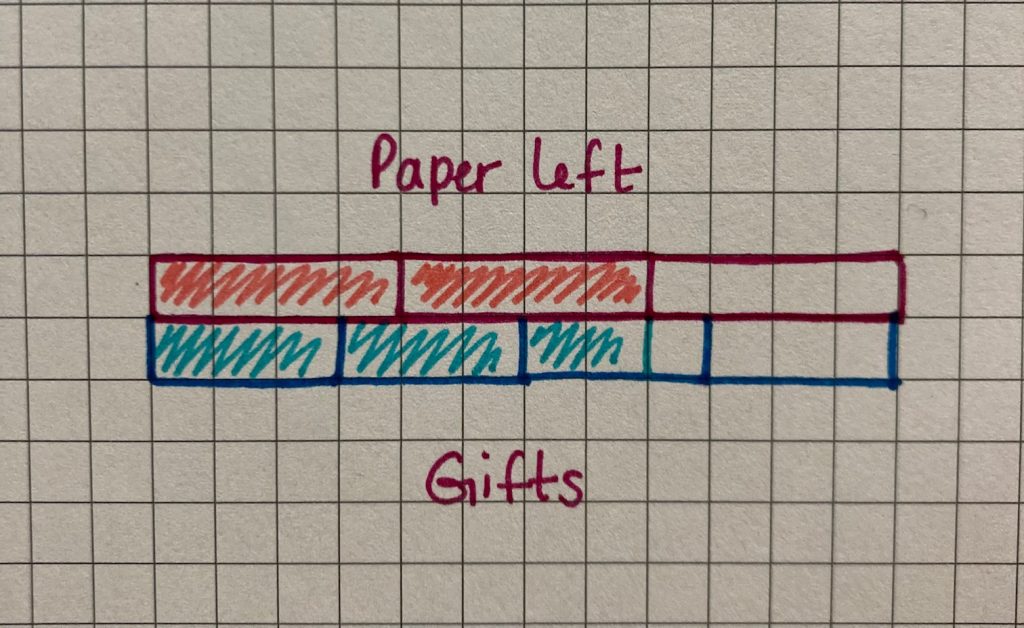
Ultimately, we have designed this prompt to allow students to bump into dividing fractions through quotative division leveraging the area model and skip counting.
Here is a short silent solution animation to help visualize this quotative division problem:
After you have had an opportunity to make connections between some of the student solutions and the equivalence, land on the following question:
What operation was used to determine the number of servings in two and one-half pizzas?
How could we represent this context as an equation?
Although students tackled this task through reasoning and visual representations, now is your opportunity to explain the context using mathematical language.
2 \(\frac{1}{2}\) pizzas ÷ \(\frac{1}{5}\) pizza/serving = 12 \(\frac{1}{2}\) servings
Here is another short silent solution animation to unpack this quotative division equation:
You might consider explicitly naming this division context as quotative division. When you are diving through quotative division, the dividend and the divisor have the same unit (pizza and pizza). Often, you are dividing by a rate (pizza/serving) to reveal the number of copies or iterations of that rate.
If your students are unfamiliar with the two types of division, consider reviewing the unit “Niagara Falls”.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt:
One-third of a small bottle of lemonade is used to fill each glass. If there are three and one-half small bottles of lemonade left, how many glasses can be filled?
Model this context to assist you in determining the number of glasses.
Represent the context as an equation.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!