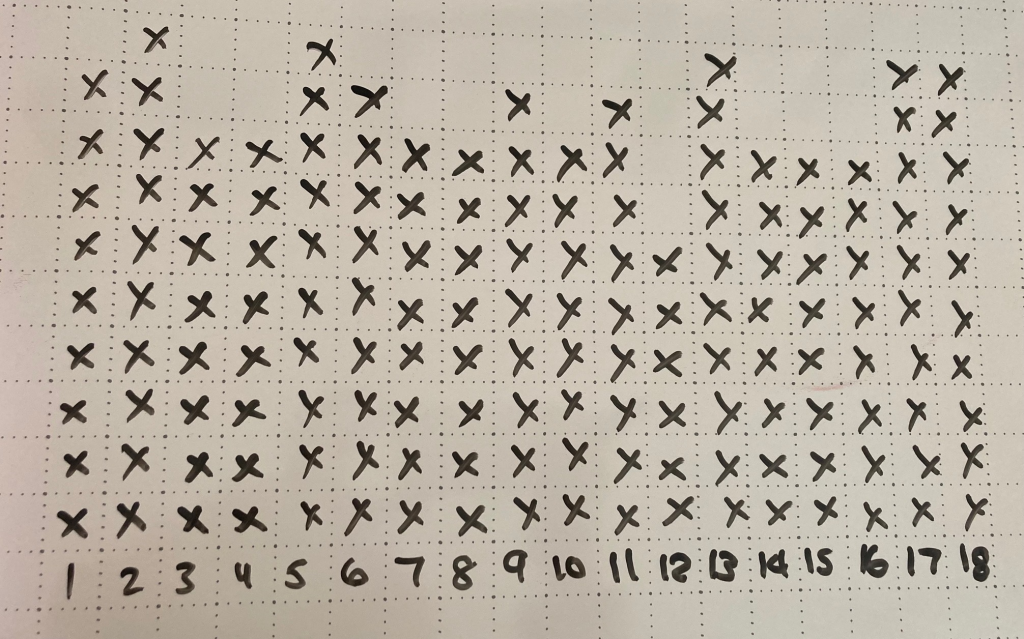OLYMPICS
DATA AND MEASURES OF CENTRAL TENDENCY
Dive into this 5-Day Problem Based Math Unit focused on data literacy including graphical representations and measures of central tendency.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview
Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
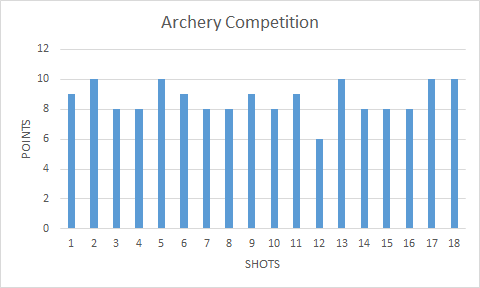
Students will create a graphical representation of an archer’s points for each shot during two phases of an event. Students will select a single value to summarize their typical score by determining an appropriate measure of central tendency.
Intentionality…
In this task, students will explore discrete data. An archer’s points are discrete because they are countable and can only take on a specific value. Based on the characteristics of this data, students will be asked to select an appropriate graph and represent. They will also use a measure of central tendency to summarize the archer’s average score in each phase in order to predict this cumulative score after twelve phases. Some of the big ideas that may emerge in today’s task include:
- There are different types of data;
- Data is often characterized as continuous or discrete;
- Discrete data is often countable and can only take on certain values;
- A measure of central tendency for a data set summarizes all of its values with a single number.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students this video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group.
Some of the noticing and wondering that came up in a class recently included:
- I notice a target.
- I notice arrows landing on the target.
- I notice points on the side.
- I notice the first arrow was 9 points.
- I wonder if this is the same person shooting the arrows or different people.
- I wonder how you win.
- I wonder how many points they will get.
- And many more.
At this point, you can answer any notices and wonders that you can cross off the list right away.
Next, verbally share the following information and share the visual prompt at the same time:
Scoring in archery is simple: just add up the number of points based on where your arrows hit the target.
The highest score for a single arrow is 10 for hitting the inner gold ring and one point for hitting the outer white ring. Arrows missing the target altogether do not score at all.
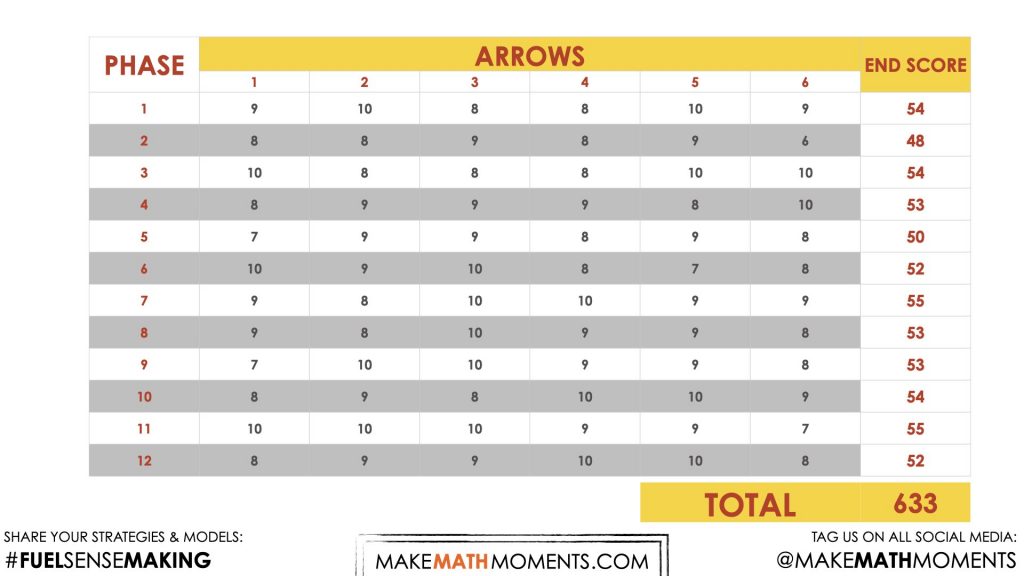
In Olympic competition athletes must shoot 72 arrows over 12 phases, with the overall cumulative score deciding their ranking
Share the following Spark Prompt with students:
If each archer must shoot 72 arrows altogether over 12 phases, how many arrows are shot per phase?
Spark Prompt Reveal
Share the following silent reveal video that quickly reveals all 72 shots over 12 phases:
Students will see that there are 6 arrows shot per phase.
Estimation: Prompt
Next, we can share the following estimation prompt with students:
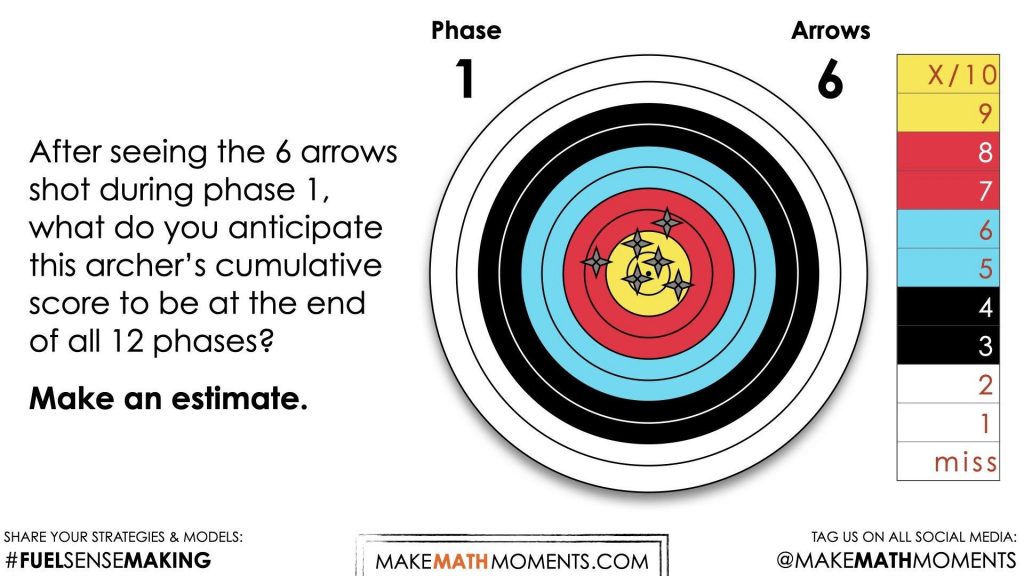
After seeing the 6 arrows shot during phase 1, what do you anticipate this archer’s cumulative score to be at the end of all 12 phases?
Make an estimate.
We can now ask students to make an estimate (not a guess) as we want them to be as strategic as they can possibly be. This will force them to use reasoning to try and come up with a reasonable estimate for 72 arrows. Students may even begin using a measure of central tendency for phase one to determine a reasonable cumulative score.
Consider asking students to think about a number that would be “too low” and a number that would be “too high” before asking for their best estimate in order to help them come up with a more reasonable estimate.
Let them chat with their neighbours and challenge them to an estimation duel or a math fight.
While Students Are Estimating…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Encourage students to use precise mathematical language and listen for the use of measures of central tendency. If students do not consider how many points the archer usually scores in one shot, you may nudge them in this direction through questioning. About how many points does the archer typically score in a single shot? What is his most consistent point value?
Allow students to share their estimates with neighbours first, then with the class. Write down their estimates on the chalkboard/whiteboard/chart paper so students feel their voices are being heard and so they feel they have a stake in solving this problem. At this point, highlight the idea of using a single value to summarize the archers points earned per shot and how this information might be helpful.
Tell students that you will not be sharing the exact score just yet.
Fuel Sense-making
Crafting A Productive Struggle:
Since you have already taken some time to set the context for this problem and student curiosity is already sparked, we have them in a perfect spot to help push their thinking further and fuel sense making.
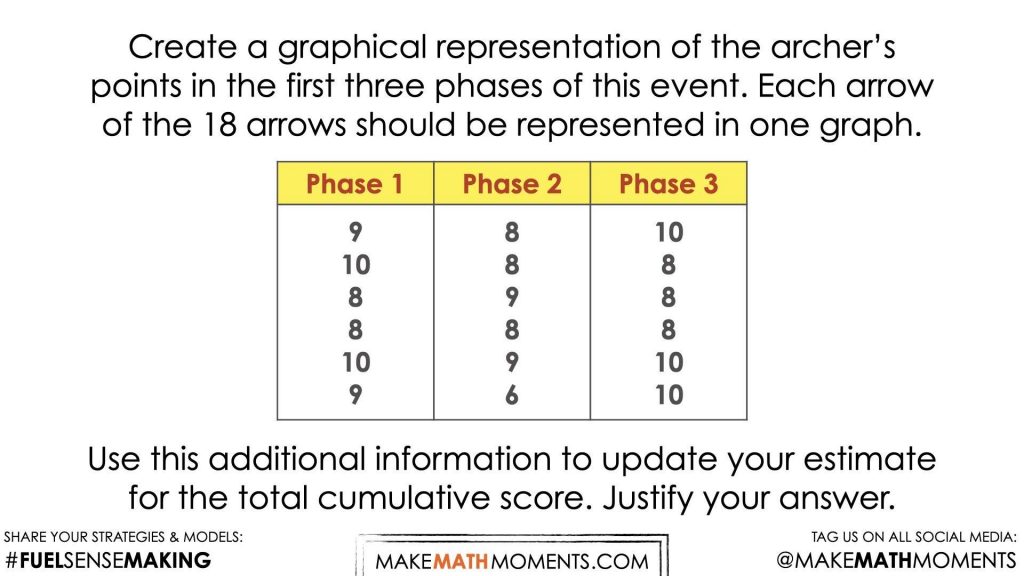
Share the archer’s points for the first three phases of this event via this animation:
You can verbally share the following information with students also:
Create a graphical representation of the archer’s points in the first three phases of this event. Each arrow of the 18 arrows should be represented in one graph.
Use this additional information to update your estimate for the total cumulative score. Justify your answer.
During Moves
While Students Are Productively Struggling….
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common misconceptions;
- most common/frequent to least common/frequent representations; or,
- choose another approach to selecting and sequencing student work.
The graphical representations you might see students include:
- Line Plot
- Bar graph
- Pictograph
If you see students using another graphical representation such as a line graph, a histogram, or a circle graph, this would be a great opportunity to sit and conference. Engage students in a conversation about the purpose of the graph and the characteristics of this data set.
Have students share their reasoning for how to represent the data and to defend their updated estimate.
Discuss their thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a representation and justification that does not connect to their understanding.
Student Approaches
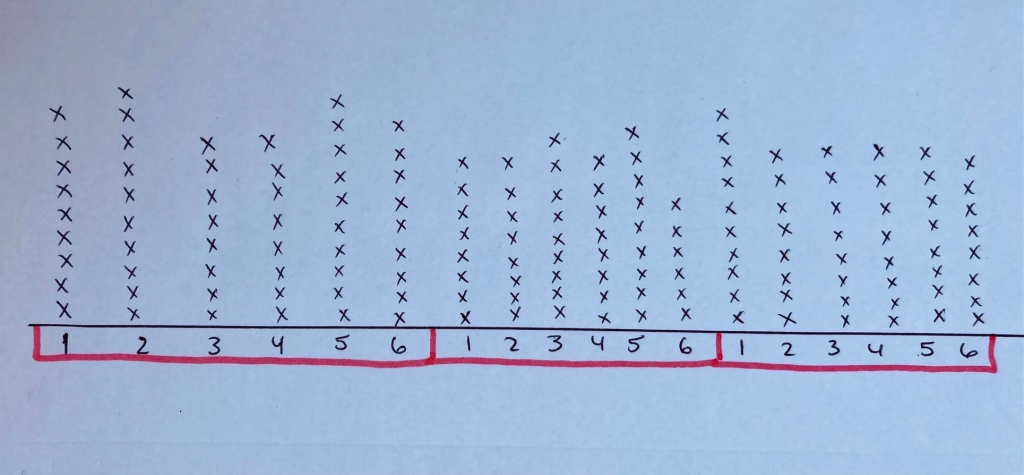
Student Approach #1: Line plot and mode
I decided to create a line plot to represent the score for each arrow. Then I noticed that the number of points that appeared the most was 8. So I guessed that he was going to score eight points a lot in the future phases. Let’s say that every arrow was 8 points, 72 multiplied by 8 is 576 points. That is my new estimate.
Student Approach #2: Line plot and mean
I used a line plot to represent the points for each arrow. Each x represents one point. I decided to rearrange the points so that all of the rows were as even as I could get them. I noticed that most of my rows had nine points. 72 multiplied by 9 is 648. I updated my estimate to 640 because not all rows have nine points.
Student Approach #3: Digital bar graph and mean
I used excel to make a bar graph. Then I took all the individual points in each phase and added them up. I added the scores for the three phases (54 + 48 + 54), and then divided the total by three to find out how many points per phase. It was on average 52 points per phase. I multiplied 52 by 12, and that gave me an estimated total score of 624 points.
Next Moves
Consolidation
During the consolidation, review the various graphical representations of the data. Discuss how a line plot or bar graph suits the data type.
Student prompt:
Why would a broken-line graph not suit this data type?
Students should begin to articulate that both variables (the shots taken and the number of points scored) are both discrete. Meaning, they can be counted, and the values can only be specific numbers. A broken-line graph would suggest the possibility of having an infinite number of values (fractional amounts) between each point. Brainstorm some other examples of discrete data.
Review the students’ strategies for updating their estimate. Select a few students to share their thoughts. You might consider selecting various measures of central tendency, for example mode and mean.
Establish a clear definition of each measure for all students, and ask them to consider which single value best represents this data set and why.
Student prompt:
How did determining a single value to represent the points scored on average help you estimate the cumulative points after twelve phases?
Give students an opportunity to turn and talk. Discuss as a whole group.
The following is a silent solution animation unpacking some of the anticipated student approaches you might see.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
Determine a single value to summarize the points scored with one arrow by the following archer in phase.
Justify your answer.
Consolidation Prompt #2:
The data set shared today was an example of discrete data.
- In your own words, define discrete data.
- Share another example of discrete data.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!