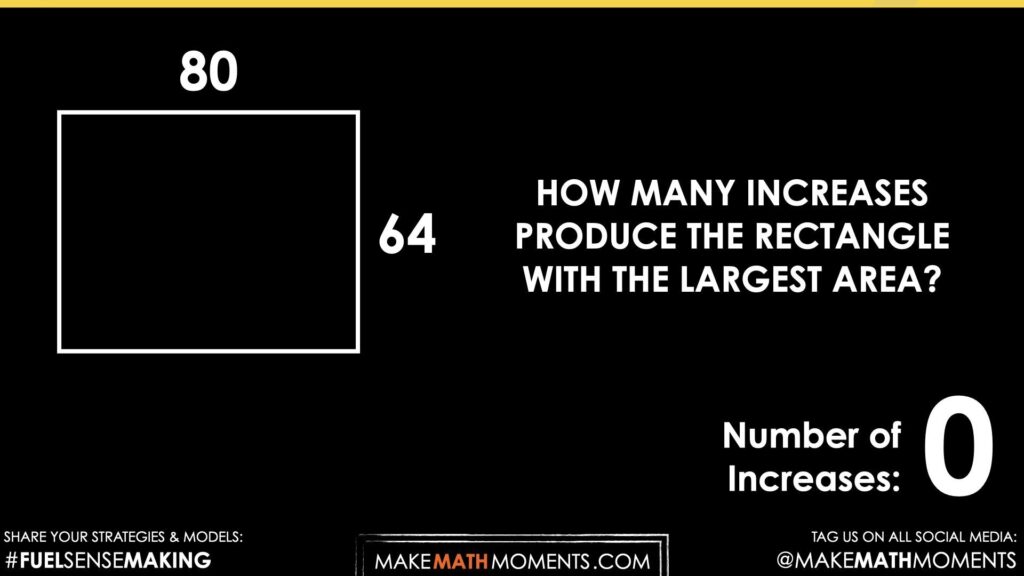MAGIC RECTANGLE
OPTIMIZATION: AREA OF A RECTANGLE
Investigate and determine the maximum area of a rectangle with constraints on the dimensions through a contextual problem-based task.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview
Length of Unit: 2 Days
Access each lesson from this unit using the navigation links below
Students will explore how the area of a rectangle changes as its dimensions change with constraints.
Intentionality…
The initial intention was to create a problem that would unpack some of the important details of quadratic equations including creating equations and manipulating between factored, standard, and vertex form as well as developing a need for the use of completing the square concretely with algebra tiles. However, this task can be accessible by students in grade 5 when working with two-digit multiplication and area, while also having the opportunity to extend all the way to optimization problems in calculus. Some of the big ideas that may emerge in this unit include:
- When side lengths of a rectangle change linearly, the area can be modelled with a quadratic model;
- Multiplying two linear models together creates a quadratic model.
- The maximum value of a quadratic model occurs at the vertex of the parabola.
- A quadratic function can have multiple algebraic forms;
- Algebraic forms of a quadratic function can be manipulated using algebra;
- Area models can be helpful when manipulating algebraic forms of quadratic functions.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students this video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group.
Some of the noticing and wondering that came up in a class recently included:
- A rectangle.
- A square at the start.
- Is the perimeter the same the whole time?
- When is the rectangle covering the most area?
- Why are we doing this?
- And many others…
Estimation: Prompt
Next, share the following image (gif) prompt and ask your students to call out when they think the rectangle has the greatest area.
Which rectangle shows the largest area?
While Students Are Estimating…
Allow students to share their estimates with neighbours first, then with the class. As a class discuss what changes are being made and how that is affecting the area?
Ask students “What information would you like to know to narrow your estimate?”
Students will likely want to know the dimensions of the rectangle and how those dimensions are changing.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Since you have already taken some time to set the context for this problem and student curiosity is already sparked, we have them in a perfect spot to help push their thinking further and fuel sense making.
Share the following animation with your students. The video shows the original dimensions of the rectangle and how the dimensions change in the first five increases.
You can verbally share the following prompt with students:
How many increases will produce the rectangle with the largest area?
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common misconceptions;
- most common/frequent to least common/frequent representations; or,
- choose another approach to selecting and sequencing student work.
The strategies you might see students use include:
- additively creating a table of values or ratio table showing how the dimensions are changing;
- building linear models for each of the dimensions;
- building quadratic models for the area;
Have students share their reasoning for determining the maximum area.
Discuss their thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a representation and justification that does not connect to their understanding.
Student Approaches
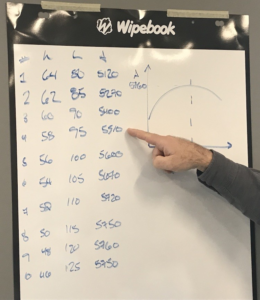
Student Approach #1: Additively Creating a Table of Values / Ratio Table
To find the maximum area I constructed a table of values to show how the width, length, and area change after each increase/decrease. You can see in my table that the maximum area occurs on the 9th image (the 8th increase).
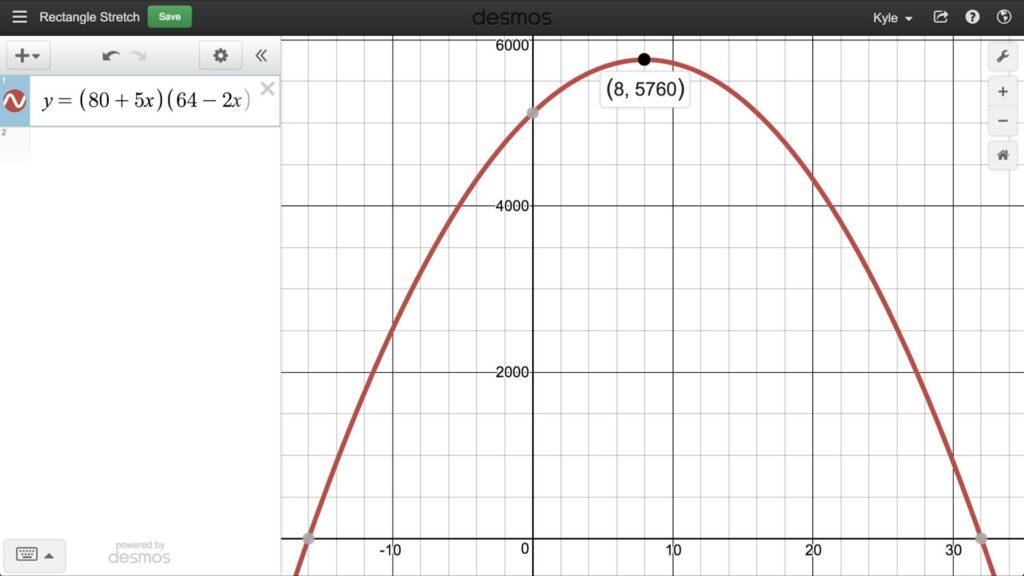
Student Approach #2: Building a Quadratic Model & Graphing With Technology
I built a quadratic equation in factored form and then graphed it to find the maximum area and the number of increases/decreases that create the maximum area.
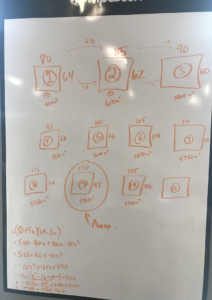
Student Approach #3: Building a Quadratic Model & Completing The Square
After creating diagrams of the rectangle and finding the areas, we built a quadratic model in factored form. We then converted the factored form to standard form and then finally to the vertex form so we could complete the square.
Next Moves
Reveal
Show students the following reveal video that reveals the maximum area of the rectangle.
You can consider sharing the screenshot of the final frame of the video as well.
Consolidation
The big idea in today’s consolidation is to examine how the relationship of the area of the rectangle as the dimensions change with constraints.
In today’s context, students likely realized that as the dimensions change with a linear pattern the area changes in a quadratic pattern.
Conclusions that we can make from this observation:
- Changing a rectangle’s dimensions linearly will result in a quadratic change in area.
- Multiplying two linear models together creates a quadratic model.
- The maximum value of a quadratic model occurs at the vertex of the parabola.
- A quadratic function can have multiple algebraic forms;
- Algebraic forms of a quadratic function can be manipulated using algebra;
Based on these findings, how can we manipulate between the different algebraic forms of a quadratic relationship?
How can we convert from factored form to standard form?
Consider using this context as a means link these forms together using an area model for multiplication.
Consider sharing the following consolidation video to highlight how to use an area model and the distributive property to manipulate the factored form of a quadratic relation to its standard form (A rectangle was chosen very specifically in this problem to elicit the use of an area model when multiplying dimensions to find the area).
How can we convert from standard form to vertex form?
Consider sharing the following consolidation video to highlight how you can use algebra tiles (a manipulative area model) to convert from standard form to vertex form. Note: this first example in this video is to show how you can use algebra tiles to complete the square with a simpler quadratic relation.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering this consolidation prompt to be completed independently.
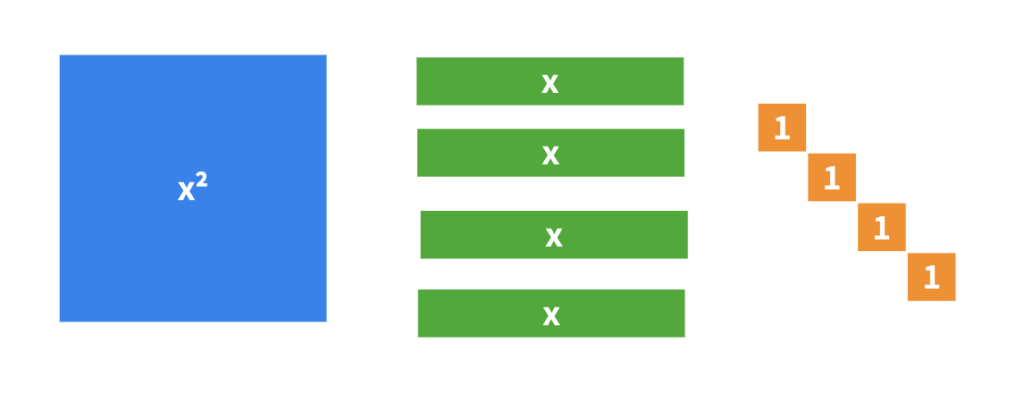
Consolidation Prompt #1:
Create a square using these tiles. Write the factored form, the standard form, the vertex form of the quadratic relation.
Note: the images used here were created using Mathigon’s Polypad https://mathigon.org/polypad
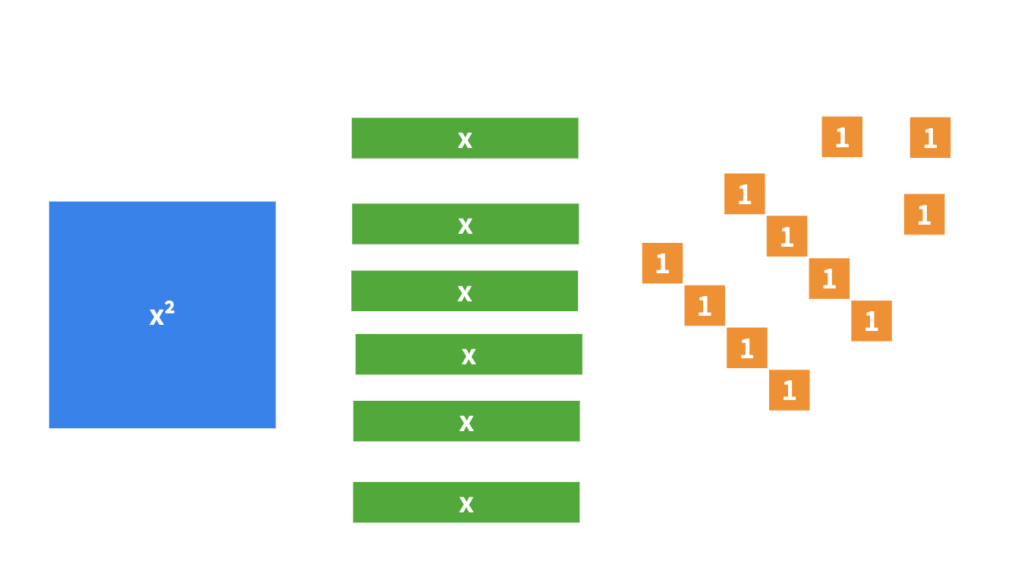
Consolidation Prompt #2:
Write the factored form, the standard form, the vertex form of the quadratic relation. Determine the coordinates of the vertex.
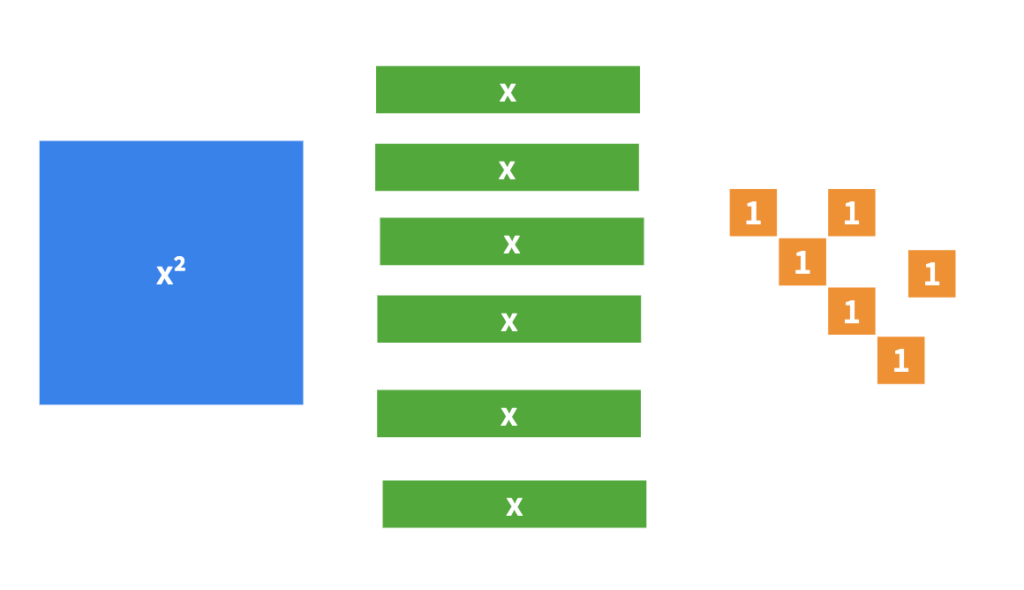
Consolidation Prompt #3:
Write the factored form, the standard form, the vertex form of the quadratic relation. Determine the coordinates of the vertex.
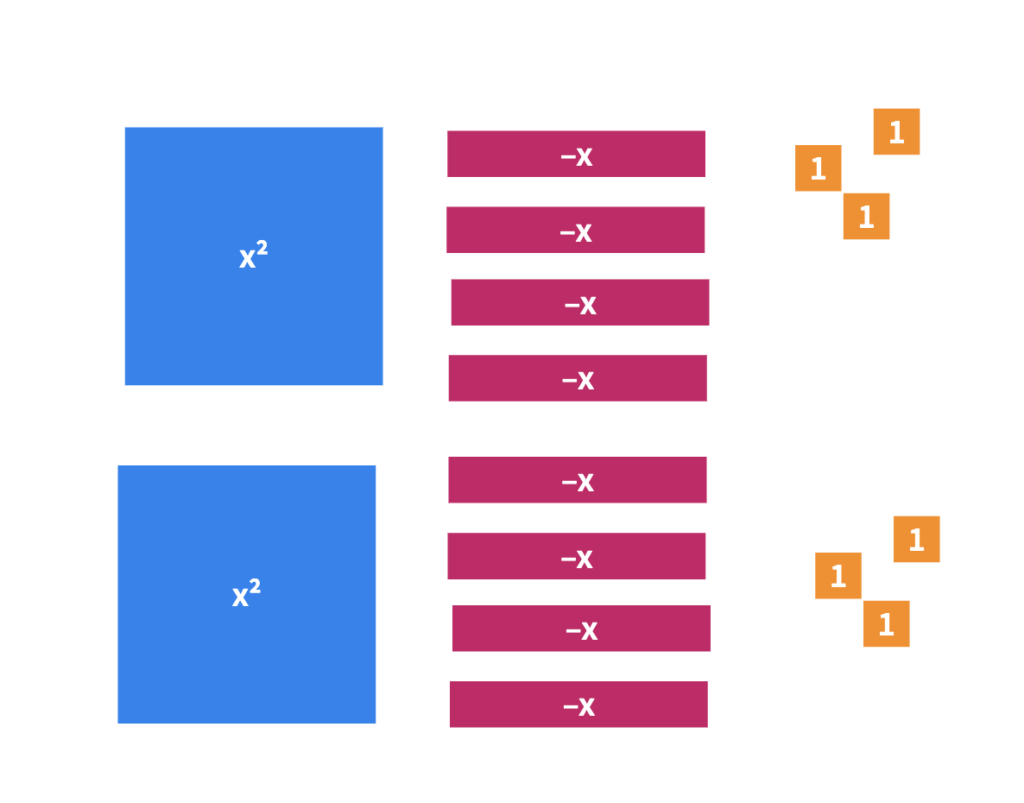
Consolidation Prompt #4:
Write the factored form, the standard form, the vertex form of the quadratic relation. Determine the coordinates of the vertex.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!
