Magic Rectangle [Day 2] - Completing The Square: Worksheet

Task Teacher Guide

Be sure to read the teacher guide prior to running the task. When you’re ready to run the task, use the tabs at the top of the page to navigate through the lesson.

In This Purposeful Practice…

Intentionality…

The purpose of the Day 2 activities is to reinforce key concepts from Day 1. Students will engage in a math talk and will have an opportunity to complete independent purposeful practice. The math talk and purposeful practice serve to develop a deeper understanding of the following big ideas.

A quadratic function can have multiple algebraic forms;
Algebraic forms of a quadratic function can be manipulated using algebra;
Area models can be helpful when manipulating algebraic forms of quadratic functions.

Visual Math Talk

Overview of This Visual Math Talk

Present the following series of Math Talk Prompts to students involving quadratic relations in standard form. Students will be asked to manipulate algebra tiles to form squares and then write the vertex form a quadratic relation. Some questions students will encounter and you should consider asking include:

What defines a square?
How can you ensure the dimensions of the rectangle are the same?
What do you need to complete the square?

You may want to consider printing out all prompts so that groups of students can progress through each prompt at their own pace. Place an answer sheet somewhere in the room so they can check their answers along the way. If you choose this set up then you’ll want to circulate around the room and monitor groups of students and be prepared to select and sequence student solutions so that you can point out “nice moves” to the whole group.

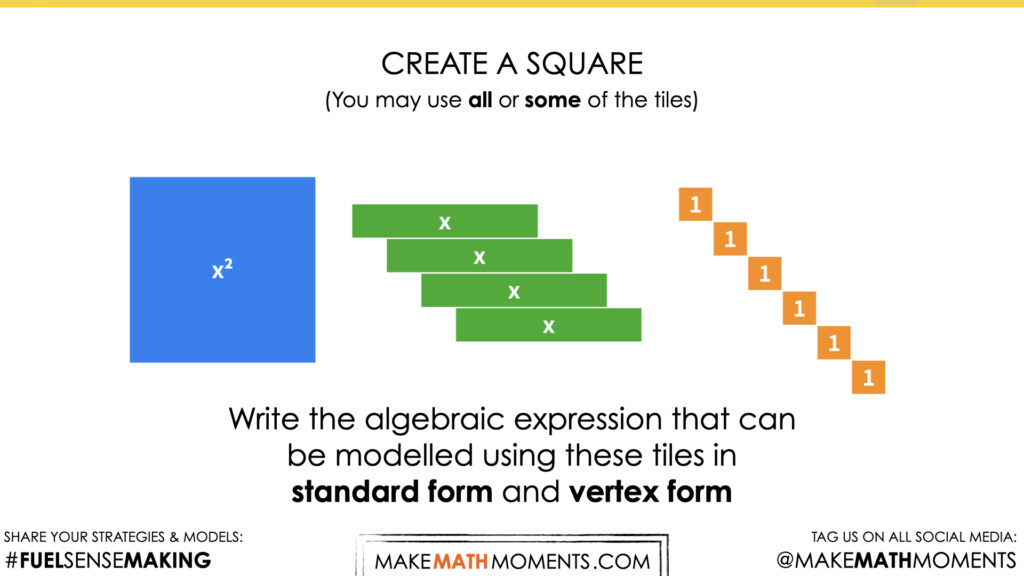
Visual Math Talk Prompt #1

Show students the following math talk prompt. You’ll notice that a series of four (4) buildings appear and students are asked:

Create a square. Write the algebraic expression that can be modelled using these tiles in standard form and vertex form.

$Completing The Square$ Students may first make rectangles instead of squares. Prompt these students with: What defines a square? How can we make the side lengths the same length? Students will become comfortable with the idea of splitting the x-terms into two groups and placing each group along side the x squared tile. This partitioning will help students link the completing the square algorithm with this visual model. Try to limit any mention of an algorithm at this point. Let students develop their own visual shortcuts and algebraic expression shortcuts. If students struggle to write the vertex form encourage them to first list the dimensions of the square. For example, they could notice that the square has x + 2 as its length and its width. “How could we write an expression for its area?”

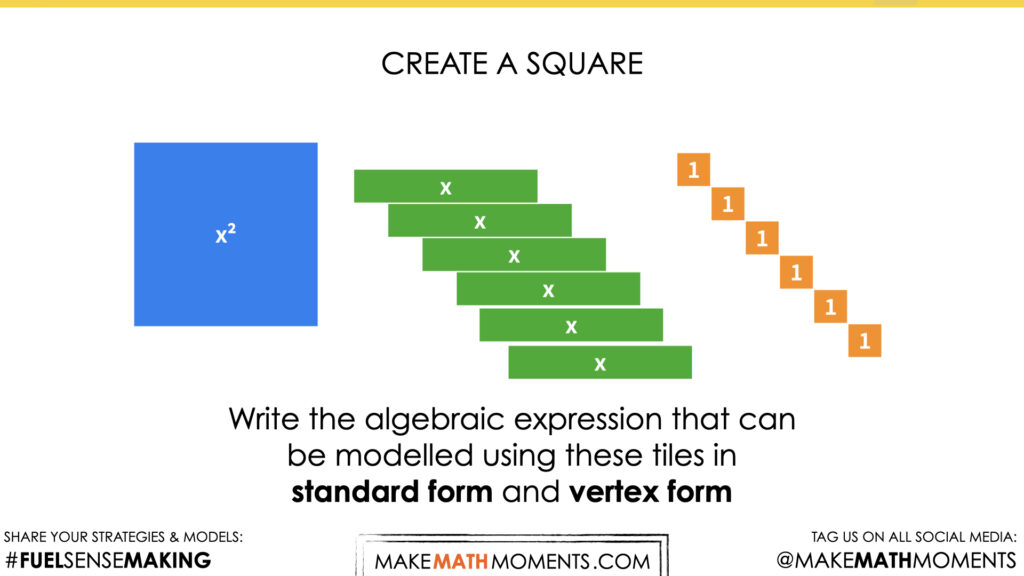
Visual Math Talk Prompt #2

Show students the following visual math talk prompt and be prepared to pause the video where indicated: Then ask students:

Create a square. Write the algebraic expression that can be modelled using these tiles in standard form and vertex form.

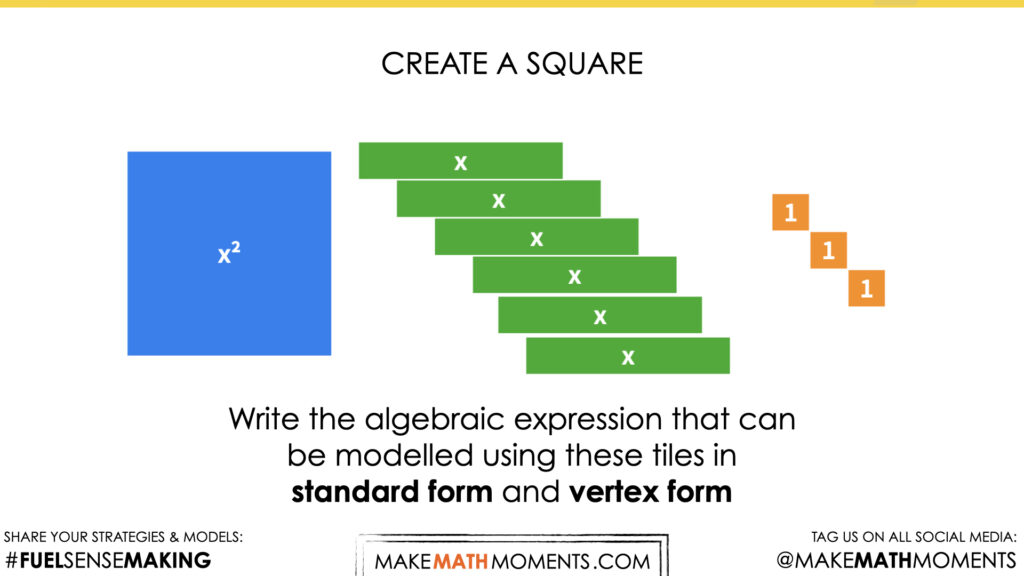
Visual Math Talk Prompt #3

Show students the following visual math talk prompt and be prepared to pause the video where indicated: Then ask students:

Create a square. Write the algebraic expression that can be modelled using these tiles in standard form and vertex form.

$Completing The Square$ Use the helpful tips and suggestions from Prompt #1 to help students with this prompt. This prompt is designed to help students practice the techniques and ideas formed in prompt #1. However, this prompt is slightly different as it will require students to use the zero principle to help complete the square. Help students understand that we will need to bring in extra tiles to create the square but will need to bring in an equal number of opposite tiles so that this new expression is equivalent to the original expression.

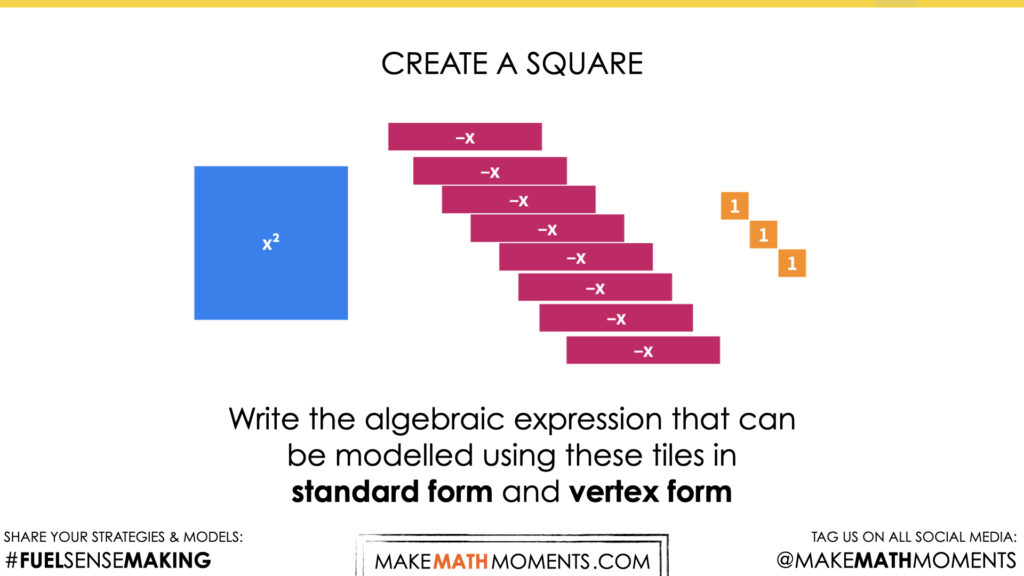
Visual Math Talk Prompt #4

Visual Math Talk Prompt #5

Visual Math Talk Prompt #6

Visual Math Talk Prompt #7

Visual Math Talk Prompt #8

Purposeful Practice

While Students Are Practicing…

Questions: Multiplication

Login/Join to access the Purposeful Practice as well as the Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units. We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.

Download Editable/Printable Handout

Become a member to access purposeful practice to display via your projector/TV, download the PDF to upload to your LMS and/or print for students to have a physical copy

JOIN TO DOWNLOAD

Resources and Downloads

Lesson Tip Sheet

Download the lesson plan in PDF format so you can keep it handy and share with colleagues. JOIN TO DOWNLOAD

Videos & Images

Hot Chocolate Task Screenshot Images.002

Download the videos, images, and related media files to your computer to avoid streaming. JOIN TO DOWNLOAD

Keynote Slides

Hot Chocolate Task Screenshot Images.003

Download in Apple Keynote format to avoid streaming video and run the lesson smoothly. JOIN TO DOWNLOAD

PowerPoint Slides

Hot Chocolate Task Screenshot Images.004

Download in Microsoft PowerPoint format to avoid streaming video and run the lesson smoothly. JOIN TO DOWNLOAD

Printable Handout

Download/Edit the handout so you can keep it handy and share with colleagues. JOIN TO DOWNLOAD

Explore The Entire Unit of Study

This Make Math Moments Task was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, and extensions to elicit and emerge mathematical models and strategies. Click the links at the top of this task to head to the other related lessons created for this unit of study.