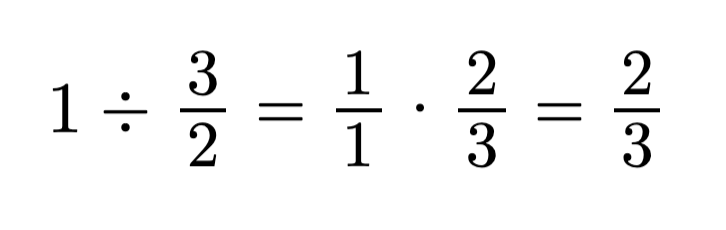LISTENING SPEED
RATE AND PROPORTIONAL REASONING
Use rate reasoning while students strengthen their understanding of fractions, decimals and percent.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview
Current Length of Unit: 1 Day*
*This lesson is the first of an expected 5-day unit. The remaining four (4) days will be released as soon as they are available.
Students will determine the listening time of an audiobook read a 1.5x the speed of the original listening time.
Intentionality…
As is true for any task, the intentionality or learning objective can vary depending on what mathematical thinking you are hoping to elicit. The purpose of this task is to engage students in problem solving with rates of change while strengthening their understanding of the connection among fractions, decimals and percent and multiplying and dividing fractions.
Spark Curiosity
What Do You Notice? What Do You Wonder?
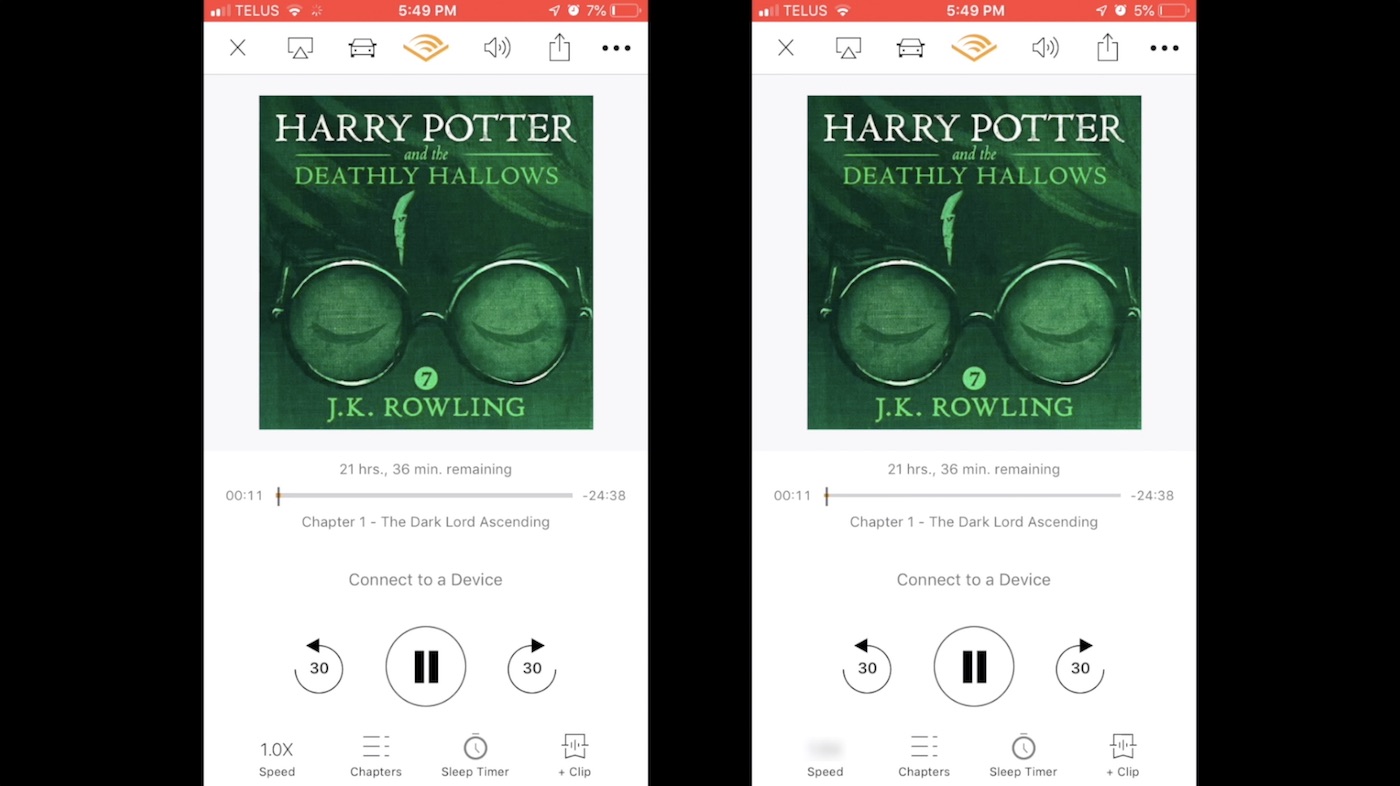
Show students the video below of two instances of an audiobook being read at different speeds, side-by-side.
Ask students to engage in a notice and wonder protocol. ANYTHING and EVERYTHING that comes to mind is fair game.
For example, students might notice and wonder the following:
- I notice that the book will take 21 hours and 36 minutes to listen to.
- I wonder what this has to do with math class.
- I noticed that there’s pictures of the same book.
- I wonder why we’re seeing two of the same book.
- I notice that one side the book is read faster than the other.
- And many others…
Document what students notice and wonder with you on chart paper, whiteboards, or other visual displays in your classroom.
Prompt & Estimate
Then, ask students:
What speed do you think the audiobook was being played during the second half of the video?
Make an estimate and share with a neighbour.
You’ll notice in the Spark tab that there is also a screenshot there for students to reference.
As we typically do when following the Curiosity Path and asking students to first estimate before solving a problem, we want to encourage students to consider quantities that are unreasonably high or unreasonably low.
For example, some students might say that a speed of 1.05x the original reading speed is too low because it would be too hard to notice a difference. Other students might say that a speed of 20x would be way too high because you wouldn’t even be able to understand what they were saying.
Facilitator Note:
Encourage students to get more risky with their range of unreasonable values to try and narrow down the reasonable range they might use to land on an estimate. If students say “1.05x”, ask students to explain what that value means as a percentage. Students who are flexible with fractions, decimals, and percentages will be able to say something like “5% faster” using additive thinking or “105% as fast as” using multiplicative thinking.
Others might be able to say “an additional 20th the speed” recognizing that 5% = 1/20 and using additive thinking. A multiplicative thinker using a fraction to describe the same increase in speed might say “21 twentieths (or 21/20) the speed of the original”.
Trying to draw on these discussions and even considering modelling using number lines or bar models is a worthwhile way to spend some of this estimation time to leverage and grow number fluency and flexibility.
If you’re looking for more on additive and multiplicative thinking as well as building number sense in your students, consider The Concept Holding Your Students Back course.
Fuel Sense-making
Estimation Reveal
Once students have shared their estimates and you’ve recorded them on a numberline on the chalk board, whiteboard, or chart paper, you can share the estimation reveal video to help lead us to our Sense Making Prompt for the day.Students should now be aware that the first “play” of the audiobook was at normal speed (1x) and the other was at a faster speed, (1.5x).
Craft a Productive Struggle
The prompt we will land on to Fuel Sense Making for this lesson is:How long will it take to listen to the audiobook at 1.5x the speed of the original?It should be noted that our prompt is being stated using multiplicative thinking, whereas some students may misinterpret additively. Have students estimate the length of time it would take to listen to the book at 1.5x speed using friendly numbers. Have students share their estimates with a class elbow partner and then to the whole class. Provide images highlighting the original length of the book at normal speed (1x) and the unknown listening time at the new faster speed (1.5x).
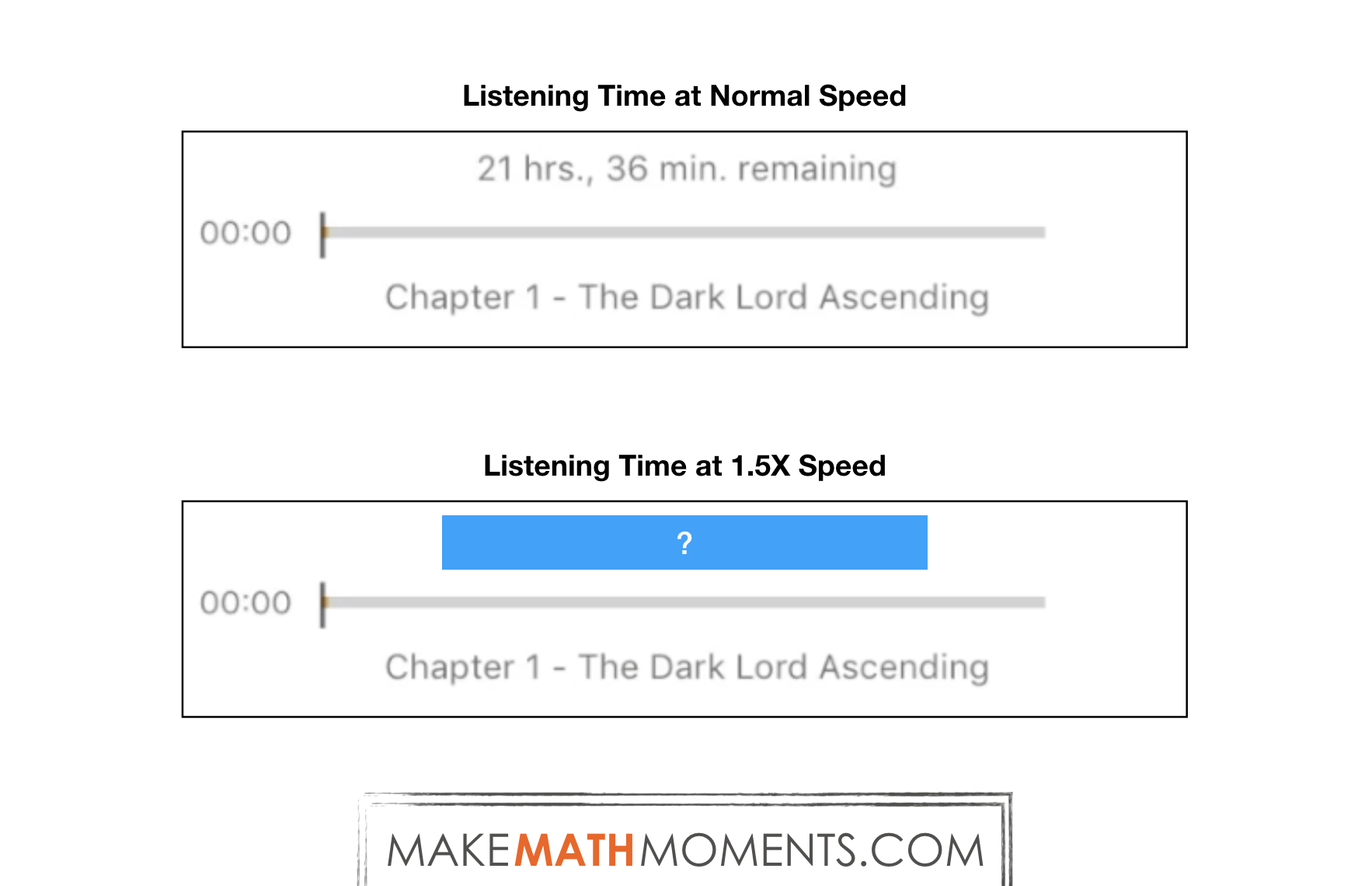Give students an opportunity to turn and talk with a partner and discuss what strategies they may need to solve this. Ask students to use this information to update their estimates. During Moves
While Students Are Productively Struggling….
Monitor student thinking by circulating around the room and listening to the mathematical discourse.
Select and sequence some of the student strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
Some of the mathematical models you might see students use as tools for thinking and to represent their thinking include:
- Concrete manipulatives (i.e.: relational rods, connecting cubes)
- Bar models
- Tables
- Symbolic notation
Have students share their strategies and reasoning for determining how long the audiobook will take to be read at 1.5x the original speed. Ask them to convince you and their peers that their answers are correct by sharing mathematical models.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
Student Approach #1: Rate Reasoning and Partitive Division
I know that the full time is 21 hours and 36 minutes.
36/60 is equal to 0.6 so the original listening time in hours is 21.6 hours.
I know that if I listened to the book at 2x the speed then I should divide the original length by 2 to get 10.8 hours or 10 hours 48 minutes.
I know that if I listened to the book at 3x the speed then I should divide the original length by 3 to get 7.2 hours or 7 hours 12 minutes.
It should take twice as long as if I read at 3 x the speed, so 14 hours 24 minutes makes sense.
Or if we listen at 1.5x the speed we should divide the original length by 1.5 to get a final answer of 14.4 hours or 14 hours and 24 minutes.
Student Approach #2: Partitive Division Symblolically
I know that the listening speed is 1.5 times as fast as the normal listening speed so the original listening time is 1.5 times longer than the faster time.
1.5(t) = 21.6 hours
The time then would have to equal 21.6 / 1.5 = 14.4 or 14 hours 24 minutes.
I divided partitively since dividing is the opposite of multiplying.
Student Approach #3:
I know that if I listened to the book at 2x the speed then I’m listening time is ½ or 50% of the original time.
So 50% of 21.6 = 11.4 hours or 11 hours 24 minutes.
I know that if I listened to the book at 3x the speed then I’m listening time is 1/3 or 33.3% of the original time.
So 33.3% of 21.6 = 7.2 hours or 7 hours 12 minutes.
If we listen at 1.5x the speed then I am listening at 1 and 1/2 speed then I should first write that mixed number as the improper fraction 3/2 and then multiply by the reciprocal:
̇
So now I need to figure out 2/3 or 66.7% of 21.6 = 14.4 hours.
You can make additional connections among speed, fractions, percent, and time with this table:
Next Moves
Reveal
After consolidating learning using student generated solution strategies and by extending their thinking intentionally, we can share what really happened with this video.
Answer: 14 hours, 24 minutes.
Revisit the student responses. If student approach #3 didn’t emerge amongst your students, lead a discussion to connect listening speed, fraction of listening time, listening time as a percentage, and final listening time.
Return to the questions you recorded from the Notice and Wonder protocol, and answer any questions that have not been answered.
Consolidation
As you plan your consolidation using student thinking from around the room, keep in mind that this task really promotes rate reasoning rather than ratio reasoning due to the changing speeds (or rate of listening). While earlier in a learners journey along the Roadmap to Proportional Relationships we want to encourage and promote a significant amount of ratio reasoning through scaling in tandem, this task is a great way to essentially force students to think using the constant of proportionality (i.e.: listening at “regular speed” has a constnat of proportionality of 1, at “double speed” it is 1/2, etc.).
Assuming you have been exploring tasks involving ratios that can be scaled in tandem using ratio reasoning, be sure to ask students why they don’t think a double number line or a ratio table would be helpful with this task?
Making a connections across the different student solutions will not be extremely challenging since the thinking will likely look fairly similar.
Reflect and Consolidation Prompts
Extend #1:
Find the listening time for listening speeds of 1.25x and 1.8x.
Extend #2:
Have students look up their favourite books on Audible.com or iTunes, or other audiobook applications and determine how fast they would need to listen to their selected book to keep the time to 9 hours total.
What You Could Do If…
Students have difficulty converting time from hours and minutes into hours, you could…
- … encourage students to stay within the hours and minutes and work from there. When they have to divide 21 hours and 36 minutes by 3 you can explore with them dividing the hours and minutes separately. Having some students work with this strategy and some students work with the strategy outlined in Sample Response 1 will allow you to show the connections and differences between the strategies.
Assessment for Learning
Watch for students who…
- …are jumping right to response #2 and ask them to represent this understanding in the table to ensure they have developed the connection between their strategy and fractions, decimals and percent.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!
