LAUNDRY DAY
ADDITION STRATEGY: PLACE VALUE TO ALGORITHM
Explore efficient strategies to add values within 50
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will be presented with an addition context and explore the place value as a strategy to solve the problem.
Intentionality…
In this task, students will engage in an addition context and lead towards using place value.
Some of the big ideas that may emerge through this task include:
- Understanding hierarchical inclusion allows for flexible composing and decomposing of numbers
- Numbers can be decomposed by separating a whole into two or more parts
- Addition names the whole in terms of the parts
- Different addition situations will elicit different strategies
- Number relationships provide the foundation for strategies to help students remember basic facts
- Models can be used to connect concrete to abstract
Before starting this unit, students should be familiar with:
- Understanding of place value
- Single Digit Addition Strategies ( e.g., 8 + 7 = 15, 6 + 3 = 9, etc)
- Adding groups of ten (e.g., 30 + 20 = 50, etc)
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following video:
Then, ask students:
What do you notice?
What do you wonder?

Give students about 30-60 seconds to do a rapid write on a piece of paper or silent individual think time.
Then, ask students to pair share with their neighbors for another 60 seconds.
Finally, allow students to individually share with the entire group. Be sure to write down these noticings and wonderings on the blackboard/whiteboard, chart paper, or some other way that is visible to all. This helps students to see the thinking of their classmates and ensures each student that their voice is acknowledged and appreciated. Adding student names or initials next to their notice/wonder is one way to acknowledge their participation and can motivate others to join in.
Some of the noticing and wondering may include:
- I notice a washing machine.
- I notice baskets.
- I notice clothes hanging.
- I wonder what is in the piles on the counter.
- I wonder how many jugs are on the shelf.
Estimation: Prompt
After we have heard from students and demonstrated that we value their voice, we can ask the estimation question.

Socks always seem to go missing. How many socks are in the basket?
Follow up that question with:
How could you convince someone that your estimation is correct?
We can now ask students to make an estimate (not a guess) as we want them to be as strategic as they can possibly be. This will force them to use spatial reasoning such as the amount of socks in a small group to help justify how many there are overall. Before collecting student estimates, students can share their estimates with neighbouring students along with the reasonings.
Consider asking students to think about a number that would be “too low” and a number that would be “too high” before asking for their best estimate in order to help them come up with a more reasonable estimate.
While Students are Estimating:
Monitor student thinking by circulating around the room and listening to the mathematical discourse. You may identify some students whose thinking would be valuable to share when the group’s estimates are collected.
Encourage students to make estimations rather than 1:1 counting each sock. The video may be paused for longer before it goes blank but we want students to make estimations based on their mathematical understanding and spatial sense.
Similar to collecting their noticings and wonderings, collect students’ range of estimates and/or best estimates along with initials or names. Having some students share justifications is an opportunity for rich, mathematical discourse.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Since you have already taken some time to set the context for this problem and student curiosity is already sparked, we have them in a perfect spot to help push their thinking further and fuel sense making.
Share the following video with the prompt.
Every Saturday is Laundry Day. The basket of 14 socks was not emptied last week and now there are more socks. After 23 socks are put into the basket, how many socks are there now?

During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Educators are looking for students that are making their thinking visible so it can be displayed during consolidation. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common misconceptions;
- most common/frequent to least common/frequent representations; or,
- choose another approach to selecting and sequencing student work.
The strategies you might see students use include:
- Direct Modeling and counting all
- Counting on
- Decomposing one addend
- Place Value
Assessment:
This checklist can be used to track formative assessment as students work. The information collected can be used to form whole group, small groups or one-to-one support models.
Early Strategy | Direct modelling and counting all | Students will count the initial value, count the amount added, and then count all of the amounts. Example: Count 1: 6 blocks Count 2: 4 blocks Count 3: 6 blocks and the 4 blocks to know 10 blocks in all |
Count On | Students are holding one number in their head and continuing to count forward and track their count | |
Single Digit Addition Strategies | Students would benefit from extensive practice with single-digit addition strategies such as 6 + 3 or 7 + 8. Educators want to watch for students who are still using a counting on strategy when solving | |
Add groups of ten | As students break up numbers using place value, they are adding tens (or more) to each other. Example: 10 + 30 or 20 + 40 | |
Place Value/ Algorithm | At first, students may break apart the numbers into place values. This requires a bigger mental load as students need to account for “regrouping/exchanging/trading” to a bigger place value. E.g., 46 + 17. A student who is using place value to add will have to trade 10 singles to make another 10. | |
Student Approaches
Student Approach #1: Counting All with a Tool
I counted out 23 blocks for the 23 socks.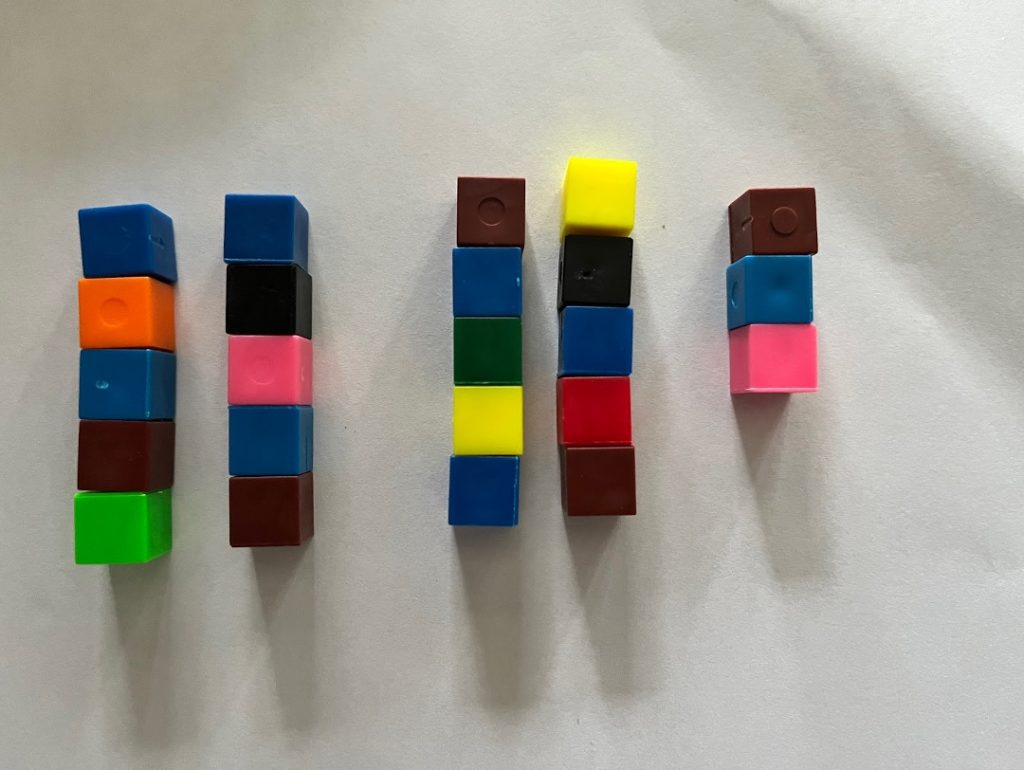
Then I counted 14 more blocks. I counted all of the blocks and there were 37. So there are 37 socks.
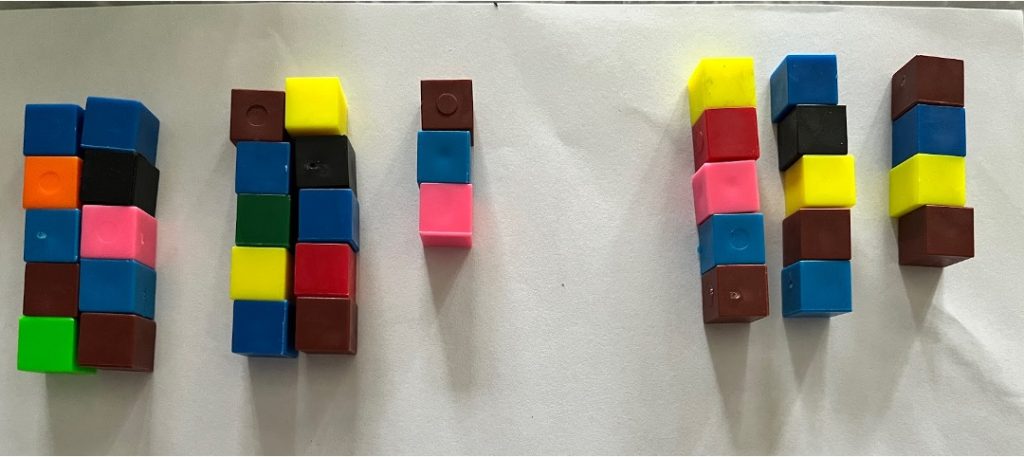
Student Approach #2: Counting All with a Tallies
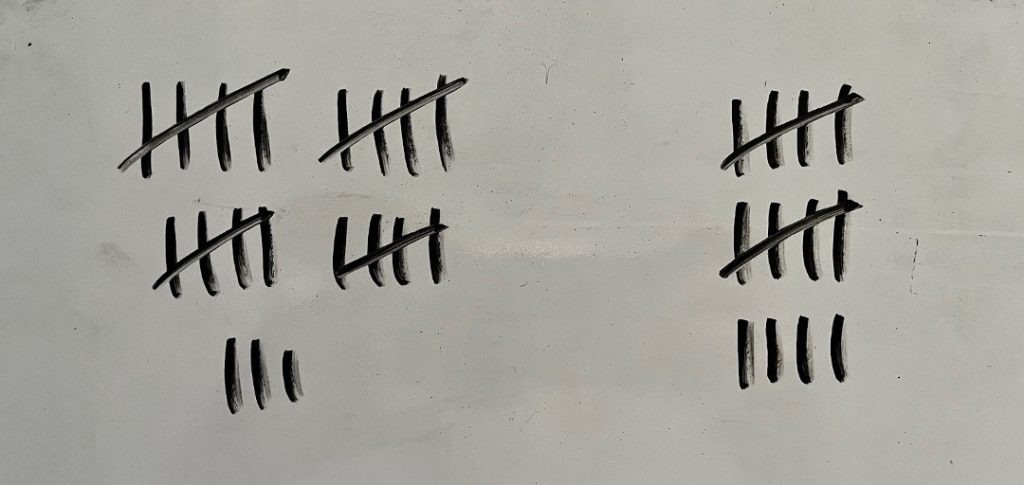
I drew 23 tallies circles for the 23 socks. I made 14 more tallies and then counted all of the tallies. There were 37.
Student Approach #3: Decomposing One Addend
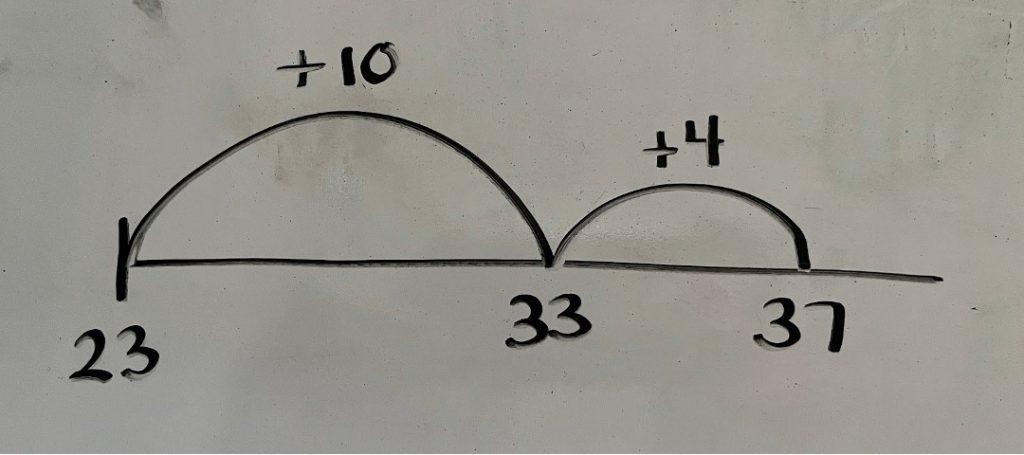
I added 10 to the 23. That made 33. I had to add 4 more to get 37.
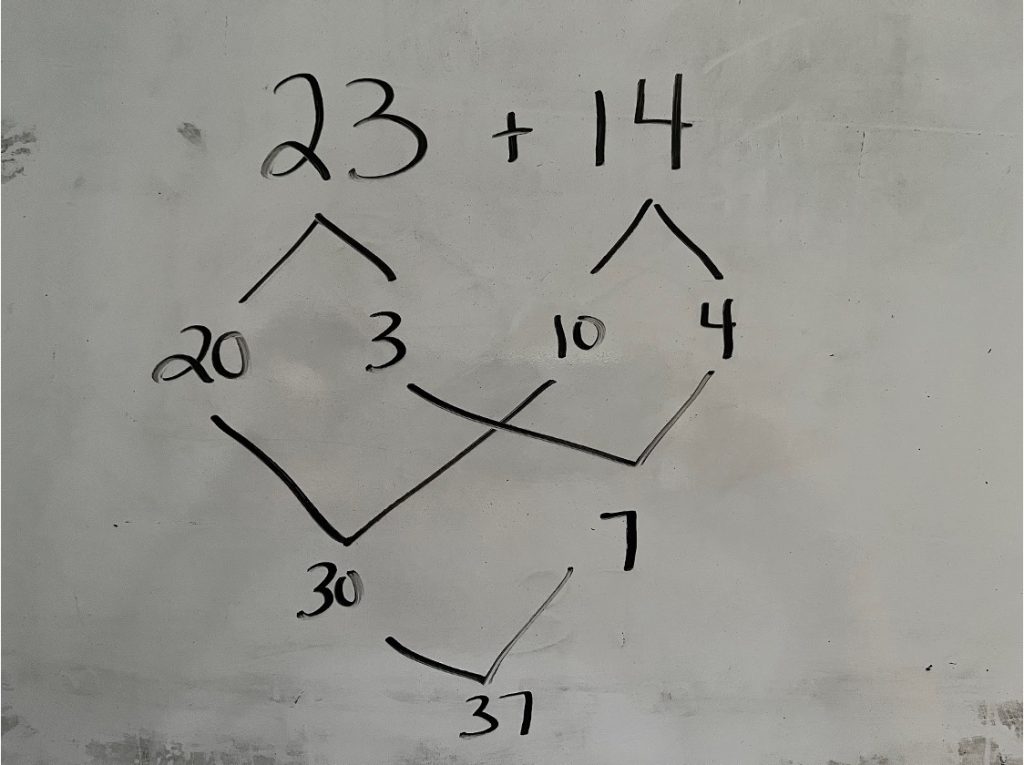
Student Approach #4: Place Value
I split 23 into 20 and 3. Then I split 14 into 10 and 4. I added the 10 and 20 to get 30. Then I added 3 and 4 to get 7. So when I put those together, I got 37.
I added the 2 and 1 to get 3 then added 3 and 4 to get 7. I put those together to make 37.
Facilitator Note: This student may be correct in their answer but encourage students to think of the numbers in terms of their place value. Rather than saying the 2 in 23 is “two”, instead encourage them to think of it as “twenty”.
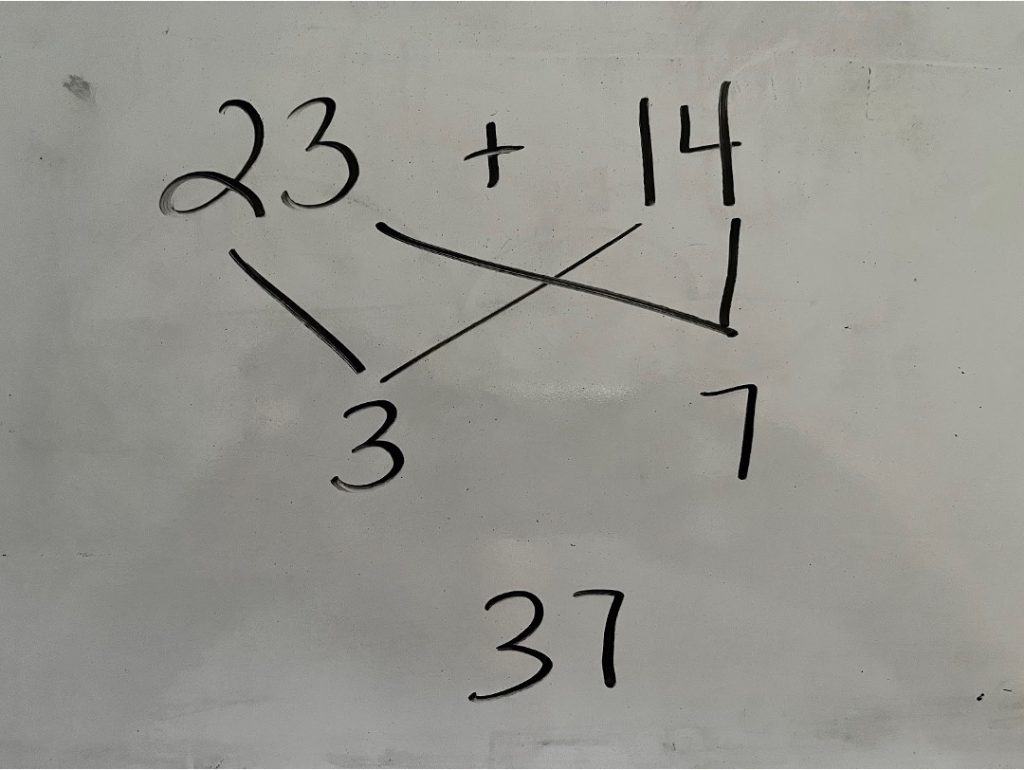
Next Moves
Reveal
Show students the following reveal video:

Facilitator Note:
The open number line (or empty number line) is an incredible tool for students to use to demonstrate their thinking. It allows flexibility from the traditional number line because students do not have to count the “ticks’ or “spaces”, instead they may jot their thinking anywhere on the line.
Notice that the arrows are going to the right or up the number line, demonstrating an increase or addition.

Facilitator Note:
This strategy uses the understanding of place value to decompose the numbers and then add each place value. By decomposing the 23 into 20 and 3 and then the 14 into 10 and 4, students are adding each place value separately. This strategy does not require a big mental load for students to solve because there is no regrouping/trading necessary. As mentioned above, unlearning needs to occur if students are mastering non-regrouping problems before learning regrouping problems. By using problem-based learning, students will develop an understanding of the process. This unit is going to get to this quickly.
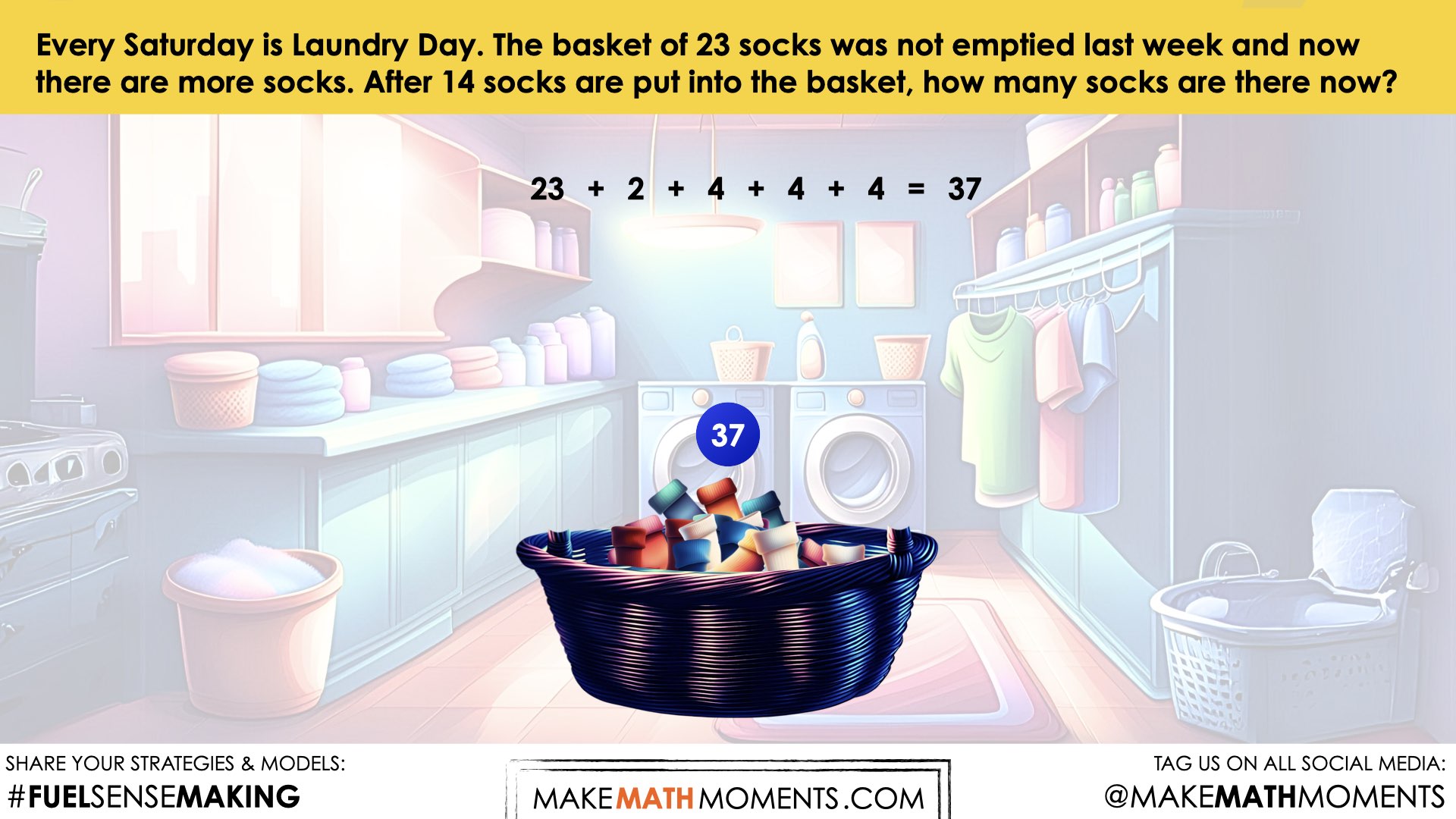
Consolidation
Consolidate learning by facilitating a student discussion.
This unit addresses splitting both numbers to add as it is usually the earliest strategy that naturally arises when students have explored place value. Place value refers to the understanding that the position of the digit represents its value. For example, the 3 in 34 is “thirty” and has a different mathematical meaning from the 3 in 23 which is “three”. Adding the tens and ones separately requires more of a mental load as the students need to hold more pieces in their memory. For this reason, as numbers become more complex and as more efficient mental strategies are explored, this strategy has less of an emphasis. This strategy will lead to the standard algorithm which is just an abstract recording of the place value strategy of “adding the tens and ones separately”.
As students learn about the idea of place value, regrouping typically makes sense. This understanding is essential as students move to more complex numbers and operations. To support this thinking, students should work with physical models that are proportional (Van de Walle, et al., 2014). It is suggested to begin with groupable models where students can regroup/trade singles to make tens. This can be done with individual snap cubes or even popsicle sticks bundled with rubber bands. Ensure that pregrouped models like Base Ten blocks are not used too quickly before students have a solid foundation of constructing tens and eventually hundreds.
This unit explored a question that did not require regrouping/trading but the later days will quickly move into the questions that require regrouping/trading. Questions that require regrouping/trading need to be explored along with questions that do not need regrouping/trading. Ideally, place value can be reviewed or further explored with Day 2 activities.
During the discussion, encourage students to start by showing their work without an explanation. Classmates will use this time to understand the visual and make their own assumptions about the work in front of them. It is also an option to ask students “What do you think this group did to solve this question?”. This will engage students in the work. The group can clarify any misunderstandings.
Reflect and Consolidation Prompts
After the reveal, check back to your estimations. The purpose here is to reflect on student reasoning, not on celebrating who was closest.
Were there some estimates in the right neighborhood?
What helped those students to get close?
Consider the strategies that the students used. Perhaps a review of adding tens off the decade (23 + 10) is necessary. The strategy of breaking up one addend depends on students’ flexibility with decomposing numbers. It also relies on students applying the facts of ten to other decades, in this case adding from 33. Further review through number talks or games that work with the facts of ten may be helpful.
The place value strategy likely occurred naturally through student discussion. As it is being highlighted throughout the unit, it may be helpful to discuss that portion of the reveal if students did not use that strategy. As students explain their thinking during the class discussion, listen for and highlight their explanations and representations that demonstrate place value strategies. Look for and highlight examples of students using their understanding of tens and ones to help them flexibly solve the problem in a way that is efficient and accurate.
Consolidation Prompt #1:
How do single-digit facts such as 3 + 4 help when it comes to adding 23 + 4?
Explain your thinking.
Consolidation Prompt #2:
Another laundry basket has 32 socks. There were 16 more socks put in the basket. How many socks are in the basket?
Show your thinking.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!



