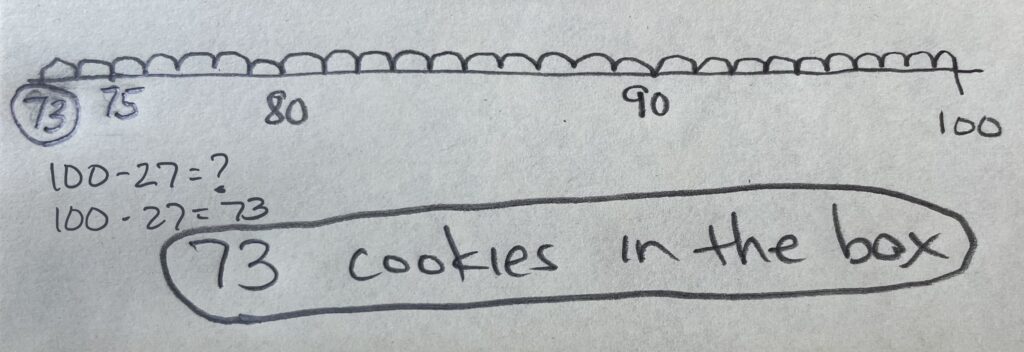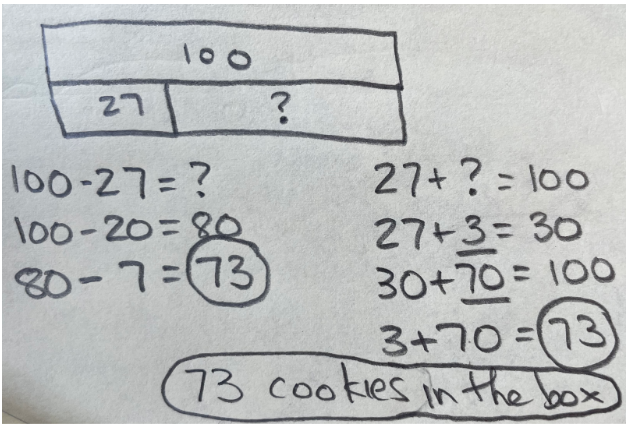HOW MANY COOKIES? HOW MANY CRACKERS?
ADDING AND SUBTRACTING WITHIN 100
Introduction to using place value strategies to add and subtract within 100
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 6 Days
Access each lesson from this unit using the navigation links below
Students will determine how many cookies remain in the box of 100 after a handful are removed.
Intentionality…
In this task, students will determine how many cookies remain in the box of 100 cookies after a handful are removed.
Some of the big ideas that may emerge through this task include:
- The action of removal is represented by subtraction.
- Removal problems can be solved by addition or subtraction.
- Unitizing 10 single cookies into one group of 10 cookies
- Addition and subtraction problems within 100 can be solved using strategies along a developmental continuum of counting all, counting on/back, and using place value strategies.
- When students are using place value strategies to solve addition and subtraction problems within 100, they are using their understanding of tens and ones and decomposition to accurately, flexibly, and efficiently solve problems. See the Student Approaches section in this guide for examples.
Before starting this unit, students should be familiar with:
- Fluency within 10.
- Solving Result Unknown Take From story problems (eg: 27 – 5 = ?)
- Difference Unknown Comparison story problems. (eg: 25 – ? = 7)
- Understanding subtraction as an unknown-addend problem (eg: 25 – 7 = ? has the same solution as 7 + ? = 25)
- Understanding that the two digits of a two-digit number represent amounts of tens and ones. (in 25, the 2 has a value of 20 and the 5 has a value of 5)
- Composing and decomposing two digit numbers. (25 can be decomposed into 20 and 5 or into 15 and 10)
- Subtract multiples of 10 in the range 10 – 90 from multiples of 10 in the range 10 – 90
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students this video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper or silent individual think time.
Replaying the video can be helpful here if appropriate.
Then, ask students to pair share with their neighbours for another 60 seconds.
Finally, allow students to individually share with the entire group. Be sure to record these noticings and wonderings on the blackboard/whiteboard, chart paper, or some other way that is visible to all. This helps students to see the thinking of their classmates and ensures each student that their voice is acknowledged and appreciated. Adding student names or initials next to their notice/wonder is one way to acknowledge their participation and can motivate others to join in.
Some noticings and wonderings that may come up:
- I noticed a box of cookies. They’re called Biscoff I think.
- I noticed the box was unopened at the beginning of the video.
- I noticed the person took a lot of cookies.
- I noticed that there were less cookies in the box after the person took some out because the level of cookies was lower.
- I wonder how many cookies were taken out of the box.
- I wonder how many cookies were left in the box.
- I wonder how many cookies were in the box before it was opened.
- I wonder if we will get to eat some Biscoff cookies.
- And many more.
At this point, you can answer any noticings and wonderings that you can cross off the list right away. Things like “I wonder whether we will get to eat some Biscoff cookies?” can be addressed right away to show students that we are indeed listening to their contributions and that we value student voice.
Estimation: Prompt
Next, share the following visual prompt briefly and ask the following question:
How many cookies are left in the box?
How could you convince someone that the quantity you come up with is correct?
We can now ask students to make an estimate (not a guess) as we want them to be as strategic as they can possibly be. This will force them to use spatial reasoning comparing the amount of cookies in the box at the beginning and end of the video or possibly some estimation based on the cookies in the top layer. Before collecting student estimates, students can share their estimates in small groups along with a justification for the reasonableness of their prediction.
Consider asking students to think about a number that would be “too low” and a number that would be “too high” before asking for their best estimate in order to help them come up with a more reasonable estimate.
While Students Are Estimating…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. You may identify some students whose thinking would be valuable to share when the group’s estimates are collected.
Encourage students to use precise mathematical language (including greater than, less than, more, less, half, higher than, lower than, layer) to articulate their defense of their estimate.
Similar to collecting their noticings and wonderings, collect students’ range of estimates and/or best estimates along with initials or names. Having some students share justifications is an opportunity for rich, mathematical discourse.
At the end of this task, during The Reveal, revisit the estimates to see how accurate students were and to reflect on the justifications they made.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Share the following image and prompt with students:
One handful of 27 cookies was taken out of the box.
How many cookies remain in the box?
Since we’ve already invested time to set the context for this problem and student curiosity is already sparked, we have them in a perfect spot to help push their thinking further and fuel sense making.
Ask the students what information they will need and how they will use it in order to find out how many cookies remain in the box. Here we are asking students to envision a solution path. By considering what information will be needed and how it can be used to solve the problem, students are being asked to make sense of the problem and reason abstractly and quantitatively (Math Practices 1 and 2). By not simply providing this information, we are inducing students to engage more deeply with the problem and think about all of its parts, known and unknown, before they begin crunching the numbers.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. At this time, teachers are looking for clear representations of student thinking to display later during the whole class discourse. In order to have a rich discussion later in the task, it is vital that teachers are intentional when they select a few work samples to share.
As students work to find out how many cookies are left in the Biscoff box, teachers can use some of their time to guide students who are struggling towards tools that might help them move forward towards a solution. However, during the majority of the student working time, it is essential for teachers to thoughtfully select some of the student solution strategies. After making a selection, ask a student from the group if they will be willing to present the group’s thinking during the whole class discourse.
Teachers should then sequence these work samples in a way that structures the discourse. Some possible ways to sequence the work samples include:
- Most accessible to least accessible solution strategies and representations.
- Most common/frequent to least common/frequent strategies and representations.
- From concrete to pictorial to symbolic representations.
- Side by side simultaneous views that can highlight one key difference that is essential to finding a solution.
- Choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Concrete representation of the 100 cookies with cubes or other tool.
- A drawing of 100 single cookies.
- A Base 10 block drawing representing the cookies in groups of ten and some ones { ⎢ , ⌑ }.
- An open number line diagram.
- A bar model diagram showing the whole and parts.
- Addition or subtraction equations that show place value strategies.
Student Approaches
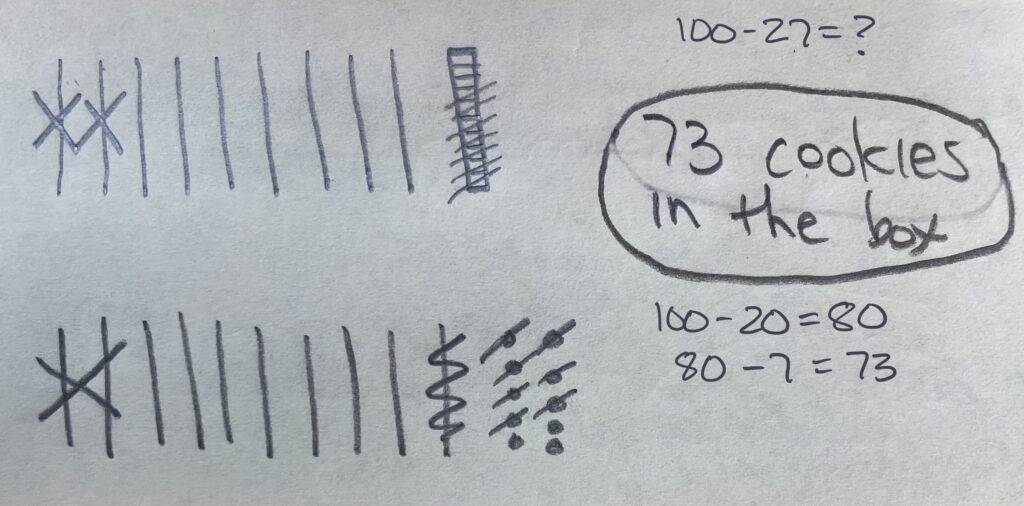
Student Approach #1: Counting All with a Tool
I counted out 100 cubes. Then I removed 27 cubes from the 100. I counted the remaining 73 cubes.
or
I counted out 100 cubes. Starting at the 28th, I counted out how many cubes there were until I got to the 100th cube.
Place Value Strategy Teaching Point: This student is not using a place value strategy. Instead of applying an understanding of tens and ones, this student is only using ones.
It may be helpful to guide this student towards arranging the cubes into 10 groups of ten or into 10 ten sticks. Noting how this makes it easier to count to 100 may help this student to see the value of working with units of ten. Similarly, to remove the 27 cubes the student can be encouraged to think of a shortcut for taking away 20 (2 ten sticks) and then taking away 7 from one of the ten sticks.
Counting the remaining cubes by tens (10, 20, 30, etc) and then adding on the singles may also help support their movement towards unitizing and using place value strategies.
Student Approach #2: An Open Number Line Diagram for Counting Back/Up by Ones
I used the open number line. I started at 100 because there are 100 cookies in the box. Then I counted back 27 by ones because 27 cookies were taken out. You don’t have to show all of the numbers on an open number line, but I showed some to help me keep track.
Place Value Strategy Teaching Point: This student is not using a place value strategy. Instead of using an understanding of tens and ones, this student is only using ones. In a respectful way, it will be helpful to have students discuss the challenges of working by ones. Students will often note that working by ones makes it more likely to miscount or make a mistake. It also takes longer and is harder! While it is part of the developmental path, this strategy is less accurate, less efficient, and less flexible than place value strategies.
Student Approach #3: Base 10 Block Drawing to Represent Place Value Thinking
(Top Example) I showed the 100 cookies by drawing 10 ten sticks. Then I crossed out 2 of the sticks. That was taking 20 cookies out of the box. Then I needed to take away 7 more cookies but all I have are ten sticks. So, I made one ten stick (the last one) thicker and cut it into ten pieces so that you can see all of the singles. I crossed out 7 of those. So, 3 singles are left and 7 ten sticks. That’s 3 and 70 which makes 73 cookies left in the box.
(Bottom Example) I drew 10 sticks of ten for the 100 cookies. I needed to take away 27 cookies. I took away 20 cookies by crossing out 2 sticks of ten. That left 80 cookies in the box. Then I needed to take away 7 more cookies. Since I didn’t have any singles, I crossed out a ten stick and drew ten singles. That’s a fair trade. It’s still 80 cookies in the box, 7 sticks of ten and ten singles. 70 + 10 = 80.
I took away 7 cookies by crossing out 7 of the singles. That left 7 sticks of ten and 3 singles which is 73. So, there are 73 cookies left in the box.
Place Value Strategy Teaching Point: These students applied their understanding of place value to subtract the tens and ones separately. By decomposing the 27 into its place value parts of 20 and 7, these students were able to work with greater efficiency and accuracy than Student Approach #2. The top example student subtracted the 7 by breaking the ten stick into ten parts. The bottom example student made a trade of one group of ten for ten singles. These are both effective strategies for regrouping situations.
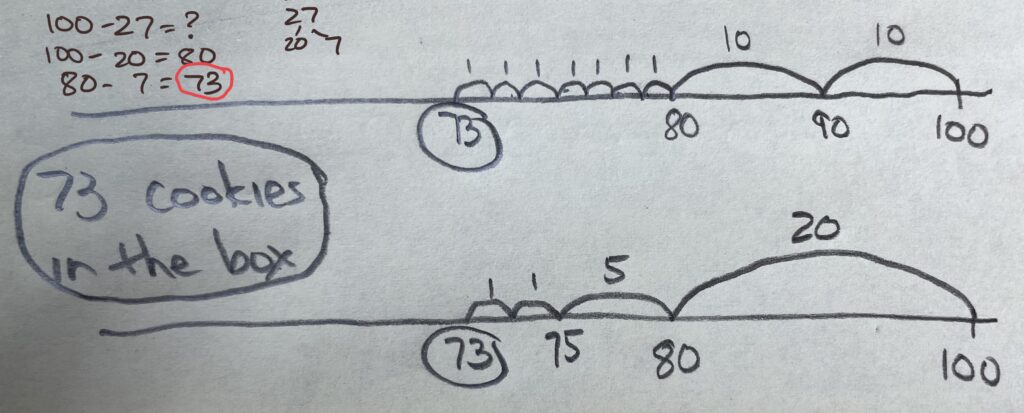
Student Approach #4: An Open Number Line Diagram to Show Place Value Strategies for Taking Away
(Top Example) I used an open number starting at 100 to show the 100 cookies in the box. To take away 27, first I took away 10 to get to 90 and then another 10 to get to 80. Now there are 80 cookies in the box. Then I counted back 7 from 80 like this: 79, 78, 77, 76, 75, 74, 73. so there are 73 cookies left in the box.
(Bottom Example) I used an open number starting at 100 to show the 100 cookies in the box. To take away 27, I broke the 27 into 20 and 7. First I took away 20. That left 80 cookies in the box. I wasn’t sure about 80 – 7, so first I did 80 – 5, that’s 75 and then took away 2 more. That left 73 cookies in the box.
Place Value Strategy Teaching Point: By subtracting the 27 in parts, these students are using a place value strategy. Breaking apart allows them to first solve the easier problem of 100 – 20. Then they are able to solve 80 – 7. Although their solution paths are slightly different, both are using place value thinking to solve the problem accurately, efficiently, and in a way that makes sense for them.
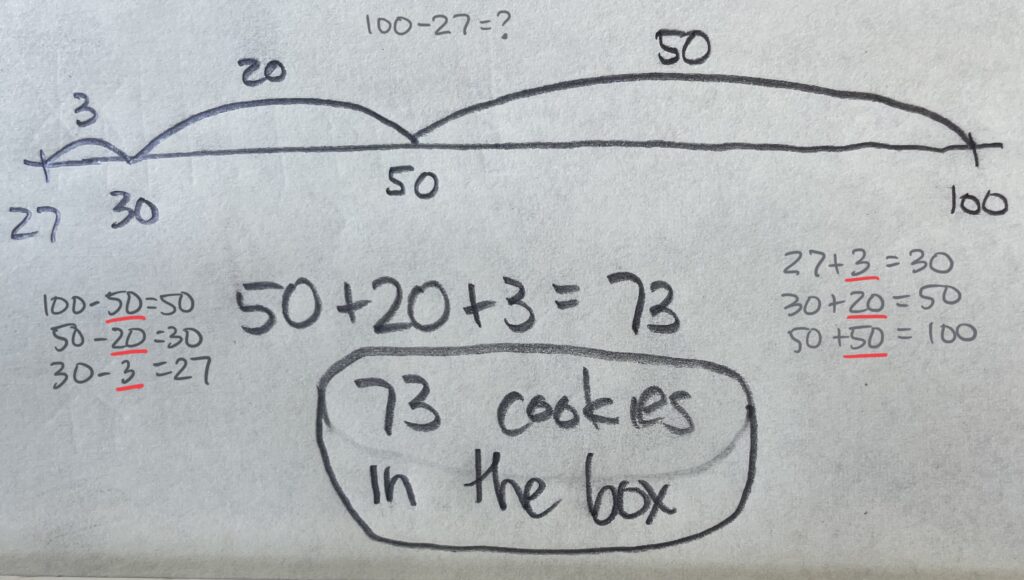
Student Approach #5: An Open Number Line Diagram Using Place Value Strategies to Find the Difference Between the Whole and the Amount Taken Away
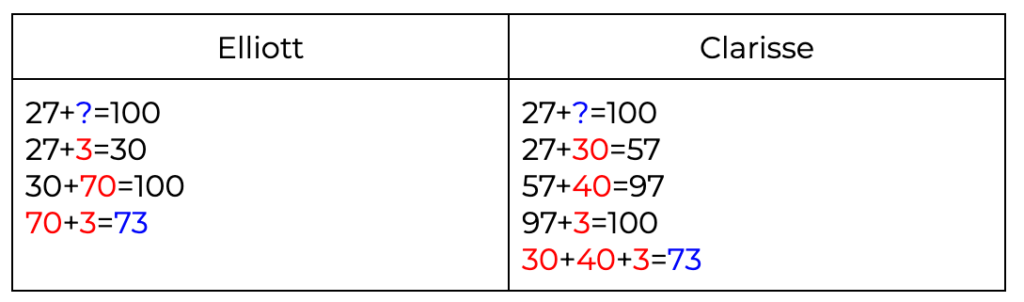
I used an open number line. I knew that there were 100 cookies in the box and 27 were taken out. That’s 100 – 27 = ?. I like adding better than subtracting. I know that I can solve 27 + ? = 100 instead of 100 – 27 = ? because it gets the same answer. So I started at 27 and added up. I added 3 to get to a friendly number, 30. Then I added 20 more to get to 50. And then I added 50 more to get to 100. At the end I just added together all of those parts, 3 + 20 + 50 = 70. That means there are 73 cookies left on the box.
Place Value Strategy Teaching Point: This student is using a place value strategy to find the difference between 27 and 100. The student is also using their understanding of the relationship between addition and subtraction. As the student adds up from 27, they work with ones and multiples of ten separately. The move from adding tens to adding multiples of tens, shows a deeper understanding of the patterns and structures of the Base 10 number system. This is a nice example of Math Practice 7, looking for and making use of structures.
Student Approach #6: A Bar Model Diagram with equations
(Left Side) I drew a bar model because that helps me understand the problem better. I drew 100 in the top bar because that’s all the cookies in the box. Then I made a second bar underneath it and cut it into two parts. One part was the cookies that the person took out of the box. That was 27. The other part is the cookies still in the box. That’s what we don’t know so I made a ?.
So, I know 100 – 27 will equal the number of cookies in the box. I solved that in parts 100 – 20 = 80 and 80 – 7 = 73. So there are 73 cookies left in the box.
(Right Side) I drew a bar model because that helps me understand the problem better. I drew 100 in the top bar because that’s all the cookies in the box. Then I made a second bar underneath it and cut it into two parts, the cookies taken away and the cookies remaining in the box. Together those will equal 100.
From the drawing I can see that 27 + ? = 100. I added up in parts. First I did 27 + 3 + 30. Then I did 30 + 70 = 100. To find out how many cookies are in the box, I added the 3 and the 70 to get 73 cookies in the box. I know 27 + 73 = 100.
Place Value Strategy Teaching Point: These students use a bar model diagram to clarify their understanding of the relationship between the cookies in the box, the cookies taken out of the box, and the cookies remaining in the box. Then they apply their understanding of place value, although in different ways.
Once the relationships are clear, the student on the left subtracts by place. This strategy simplifies the work as 100 – 27 could require regrouping while 100 – 20 and 80 – 7 are simple enough for this student that they can be solved mentally.
The student on the right uses their understanding of the relationship between addition and subtraction to solve this take away situation as a missing addend problem.The student then adds by ones and then by multiples of ten.
Next Moves
Consolidation
Consolidate learning by facilitating a student discussion.
Students present their work one by one or group by group according to the sequence that the teacher determined during the Sense Making portion of the lesson. During student presentations, the teacher can promote discussion by facilitating commenting and question asking between classmates. The twin goals of discussion are to get students to engage one another and to generalize that place value strategies are an effective strategy for adding and subtracting within 100.
To promote student engagement and facilitate discussion, teachers can:
- Create a psychologically safe space to promote intellectual risk taking, new ideas, and broader participation during discussions,
- Provide guided practice in advance regarding how to present work, appropriate voice volume, how to listen, how to agree/disagree respectfully, and other behaviors and practices to promote discussion.
- Make student work easily visible by using a document camera or other tool so that the image is large enough or all students to clearly see.
- When an important point is made by a student, prompt other students to repeat/rephrase it. This encourages listening to one another and allows for an important point to be stated 2-3 times so that more people can hear it.
- Instead of answering questions asked by students, redirecting the question back to the class. This promotes student to student dialogue.
- While it is important to keep the consolidation purpose in mind, also being open to other important thoughts and ideas that arise. Honoring these rich insights builds excitement and students’ vision of themselves as mathematicians making discoveries.
To promote greater understanding of place value strategies, teachers can familiarize themselves with the following Place Value Strategies. As students explain their thinking during the class discussion, listen for and highlight their explanations and representations that demonstrate place value strategies.
Look for and highlight examples of students using their understanding of tens and ones to help them flexibly solve the problem in a way that is efficient and accurate. This will resemble the work samples in Student Approaches 3, 4, 5, or 6. In these approaches, students are decomposing the amount being taken away into tens and ones. Students can show this understanding using Base 10 block drawings, open number lines, or just equations.
It is not necessary for students in your class to use each and every one of these approaches. Rather, utilize the examples that your students come up with as the examples of place value thinking that can be discussed by the whole group. By guiding the discussion in this direction with classroom based examples, teachers will help their class to construct their own understandings of adding and subtracting using place value strategies
- Adding or Subtracting One Number in Parts
- Students who use this strategy for 100 – 27 will break the 27 into two parts by place, 20 and 7. Then they will subtract each part separately. Typically, students will first subtract the tens place number (100 – 20 = 80). Then they will subtract the ones place number (80 – 7 = 73). It is acceptable to subtract the ones first (100 – 7 = 93 and 93 – 20 = 73).
- Adding Up
- Some students may be aware of the inverse relationship of addition and subtraction. These students know that if 10 – 3 = ?, then 3 = ? = 10. These students may find it easier to add up than subtract back. To solve 100 – 27 = ?, then rewrite it as 27 + ? = 100. They will then use their understanding of place value to add on tens and ones separately. Here are two ways students might add up.
- Making an Easier Problem
- Some students like to take a problem such as 100 – 27 = ? and make an easier problem such as 100 – 30 = ? that they can solve mentally. After solving 100 – 30 = 70, these students then adjust their answer to 73 by adding back the 3 extra that they took away. These students know that it is easier to work with multiples of tens and then separately adjust back by ones to get the answer to the original problem.
- Ask questions such as,
- How did this student take away 27 from 100?
- Why did this student first take away 20 and then take away 7. Why not just take it all away at once? Why not just take away 27 ones?
- How did the student make the problem easier by showing 100 as 10 sticks of ten?
- Why did the student add 3 to 27 first?
- How did this student use their understanding of place to solve the problem?
Have students present their strategies and reasoning for how to represent the number of cookies remaining in the box. Ask them to convince you and their classmates that their answer is correct by sharing their mathematical model. It can be very effective to project the student work with a document camera or project a photo of the student work from your computer so that everyone can easily see what the presenting student is referring to. When the other students can easily see the work sample, they remain more engaged and understand more deeply.
Discuss student strategies and elicit the questions and comments of other students during your consolidation. The goal is to help them to build off of their current prior knowledge and understanding. We want students to be socially constructing their understanding in a way that makes sense for them.
Here you are listening to this discourse with an ear for what is important for your students’ emerging understanding and application of place value strategies for addition and subtraction problems.
Reflect and Consolidation Prompts
After the reveal, check back to your estimations. The purpose here is to reflect on student reasoning, not on celebrating who was closest.
Were there some estimates in the right neighborhood? What helped those students to get close? How did they think about it?
Without a lot of information, mathematicians have to make assumptions all of the time. What assumptions made some estimates way too low or way too high?
Now that we have figured out how many cookies were left in the box, what new questions does this raise in your mind? You may choose to explore one or more of these student generated questions on another day or as homework.
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
How do place value strategies help solve addition or subtraction problems with two digit and three digit numbers?
Consolidation Prompt #2:
Consider the equation below. Write a context that could be represented by this equation. Show your thinking and solve.
100 – ? = 84
Consolidation Prompt #3:
How is it possible to get the right answer by adding and by subtracting? I thought subtracting is the opposite of putting together!
Consolidation Prompt #4:
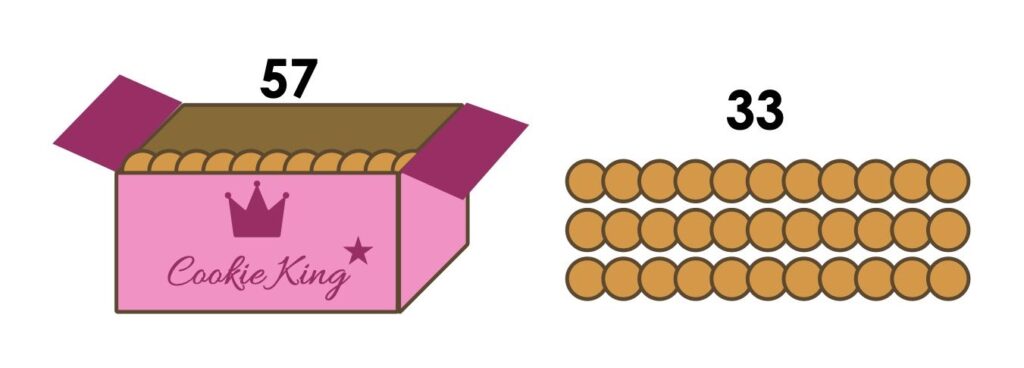
I bought a new, unopened box of cookies. I took 33 cookies out of the box. There are 57 cookies left in the box. How many cookies were in the box when I bought it?
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!