GREEN SCREEN
AREA UNIT CONVERSIONS AND PROPORTIONAL REASONING
Expand proportional reasoning skills through ratio and rate reasoning to convert area units of measure.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Current Length of Unit: 1 Day*
*This lesson is the first of an expected 5-day unit. The remaining four (4) days will be released as soon as they are available.
Students will determine how many pieces of Bristol board is required to cover a wall requiring the conversion of metric units of area.
Intentionality…
As is true for any task, the intentionality or learning objective can vary depending on what mathematical thinking you are hoping to elicit. The intention for this task when we created it was to give students an opportunity to investigate and solidify their understanding of converting between metric units of area; specifically square centimetres and square metres. However, like many rich tasks, modifying the information you provide to students and/or reframing the question you ask can allow for shifting the intentionality to a different learning goal.
This task can also be a great way to help students stretch from counting and/or additive thinking to multiplicative thinking and even build flexibility with fractional amounts. This task can also help students:
- work concretely (by cutting out scale paper versions of the wall and pieces of Bristol board), visually, and/or symbolically to apply their understanding of area as how many units of Bristol board it takes to cover the wall (counting, addition, multiplication);
- thinking fractionally by referencing the wall as the whole and determining how many pieces of Bristol board “go into” the wall (quotative division);
- apply an understanding of the unit fraction by referencing the area of the wall as the “whole” and each piece of Bristol board as a partition of the whole (partitive division);
- apply an understanding of measurement with area by determining how many pieces of Bristol board will be required to cover the wall utilizing the known measures of the length and width of the wall and the Bristol board using proportional reasoning.
As you can see from the list above, this task can be used quite flexibly from primary grades through to intermediate grades to press your students for understanding.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students this video: Ask students to engage in a notice and wonder protocol. ANYTHING and EVERYTHING that comes to mind is fair game. Here’s some of the “everything and anything” students noticed and wondered on chart paper:- I notice a work out bench.
- I notice a TV on a table.
- I notice a tripod and studio lighting.
- I notice some green Bristol board on the floor.
- I wonder if this is a workout room?
- I wonder if someone is doing a photoshoot?
- I wonder if they are making a green screen?
- And many others…
How many pieces of Bristol board will it take to cover the wall? Make an estimate.Challenge students to estimate how many pieces of Bristol board it will take. Have them share out their estimate with neighbours and ensure they attempt convincing them as to why they believe their estimate is reasonable. You might want to give students a closer look by showing the second video in the Spark tab: At this point, you must make a choice as to what information you want to share with your students. If your intention is to have your students access this task through counting, addition, or multiplication you could simply pause the “reveal” video after 1 column of Bristol board is affixed to the wall and allow students apply their spatial reasoning skills to make a prediction for the rest. You could also consider telling the students the dimensions for the length and width of the wall in “Bristol board pieces” to see if they can either create (concretely) or draw (pictorially) the array of Bristol board pieces. If your intention is to help students develop an understanding of dividing whole numbers by fractional amounts, you could reference the wall as the “whole” and tell students that 1 piece of Bristol board is 1 twenty-second or 1/22 of the wall. Students can often use their intuition to determine that they will require 22 pieces of Bristol board, which demonstrates the reciprocal relationship between dividing by 1 twenty-second and multiplying by 22. While both of the intentions above are helpful for students in earlier grades, we created this task with the intent to bring in the concept of converting metric square units. There is a lot of fun to be had here utilizing number sense and proportional reasoning.
Spark Walk-Through Videos
Watch a short video walk-through of the Sparking Curiosity portion of this task: Watch the second part of the Spark walk-through video below:Fuel Sense-making
Crafting A Productive Struggle: Prompt
The prompt in the Sense Making tab is:How many sheets of Bristol board will it take to cover the wall?Based on the intentionality we had for this lesson, we suggest that you give this information to push students to make conversions of metric units of area:
 However, you might consider sharing different linear metric or imperial measures if you believe that to be a better fit for your students:
However, you might consider sharing different linear metric or imperial measures if you believe that to be a better fit for your students:
- Version #2 Information: Metric Metres and Centimetres
- Version #3 Information: Metric Centimetres
- Version #4 Information: Imperial Inches
- Version #5 Information: Imperial Feet and Inches
Walk-Through Video
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Drawings / sketches.
- Double number line.
- Ratio table.
- Symbolic notation.
Have students share their strategies and reasoning for determining the number of pieces of Bristol board it will take to cover the wall. Ask them to convince you and their peers that their answers are correct by sharing mathematical models. Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
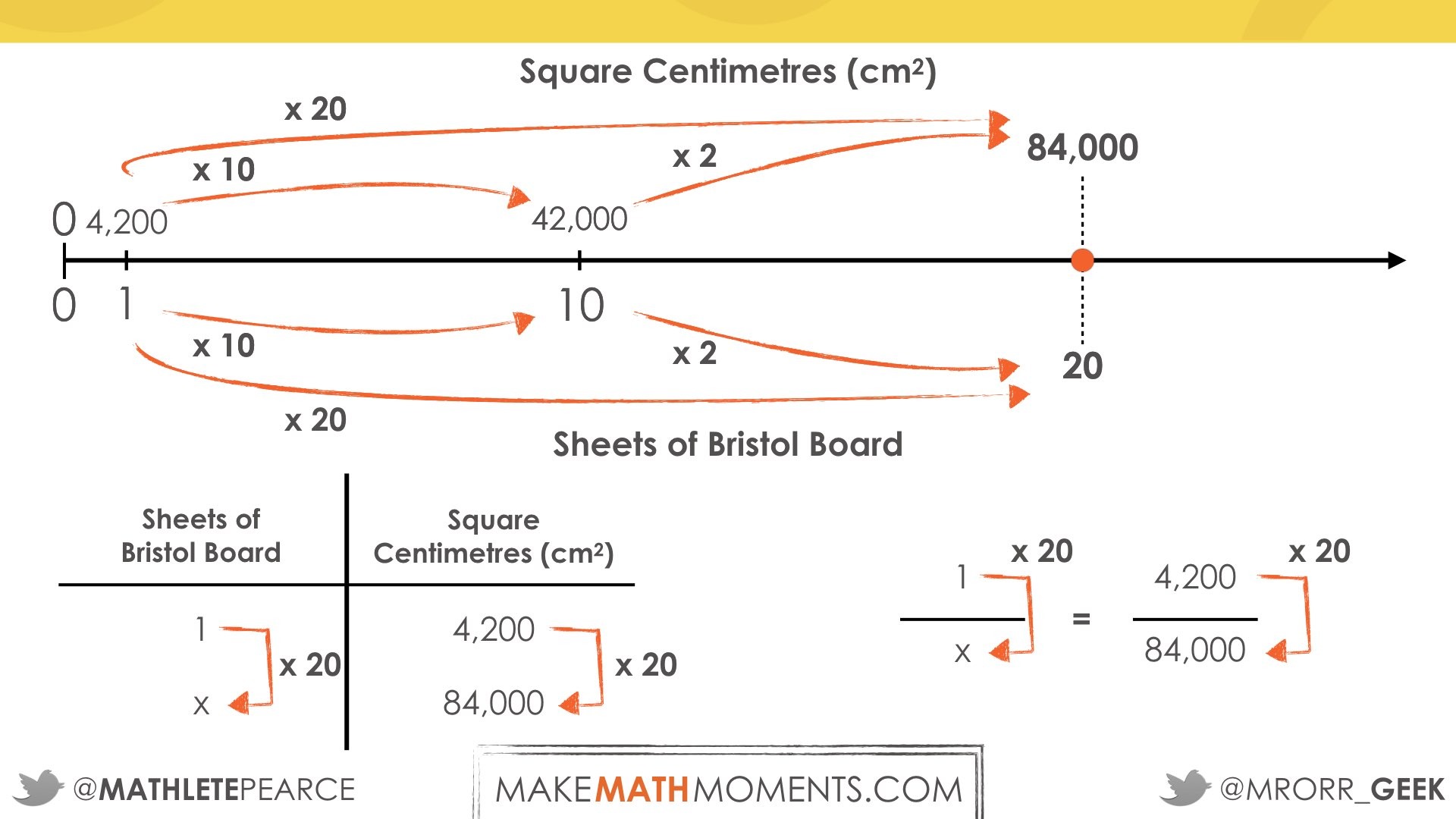
Student Approach #1: Scaling in Tandem With a Double Number Line
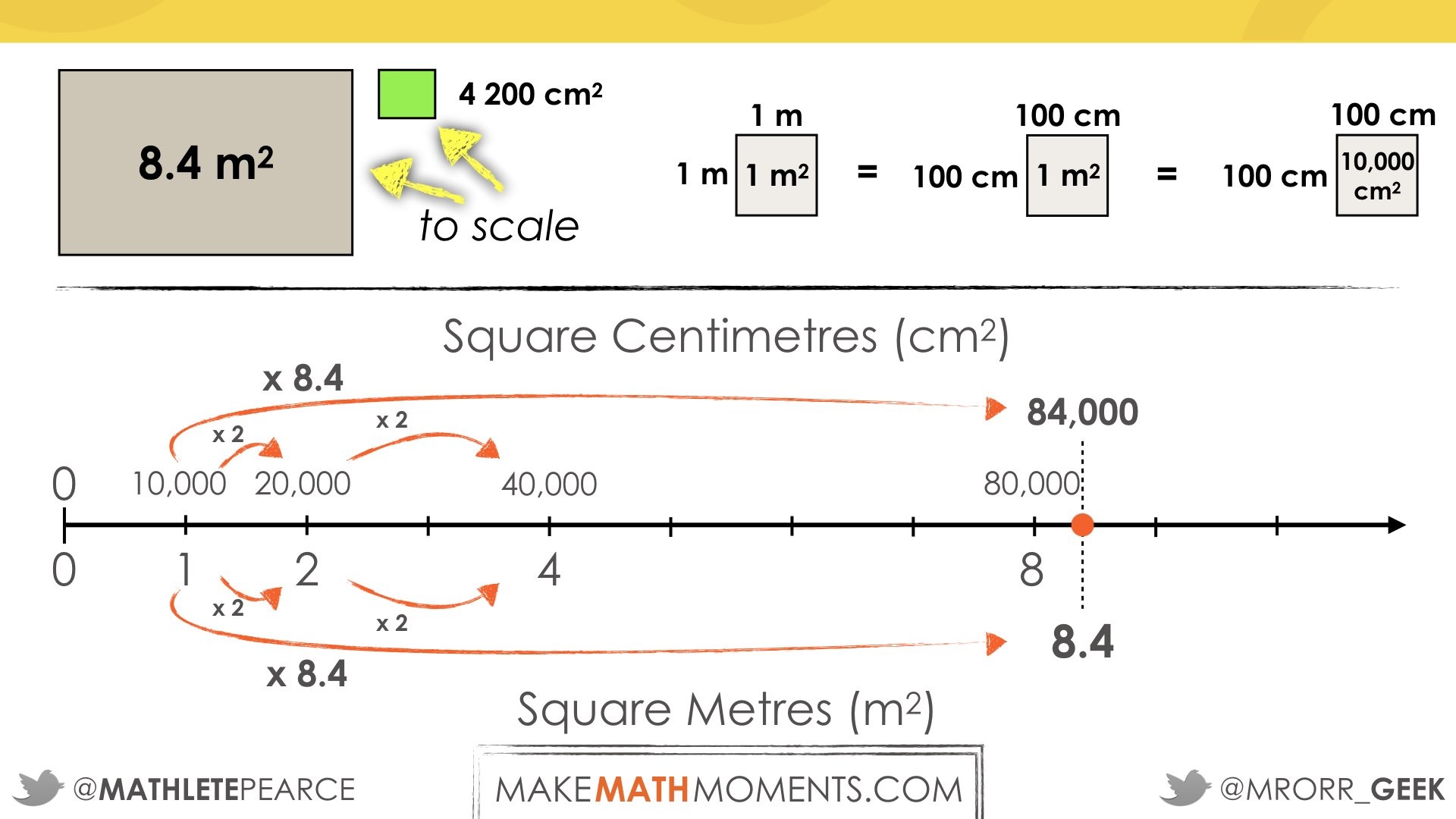
Student uses prior knowledge and understanding of the area of a square and equivalence of metric linear units to determine equivalence of metric area units using an area model (top), double number line (bottom), or similar:
Then, the student goes on to utilize a double number line to scale the number of sheets of Bristol board and square centimetres in tandem:
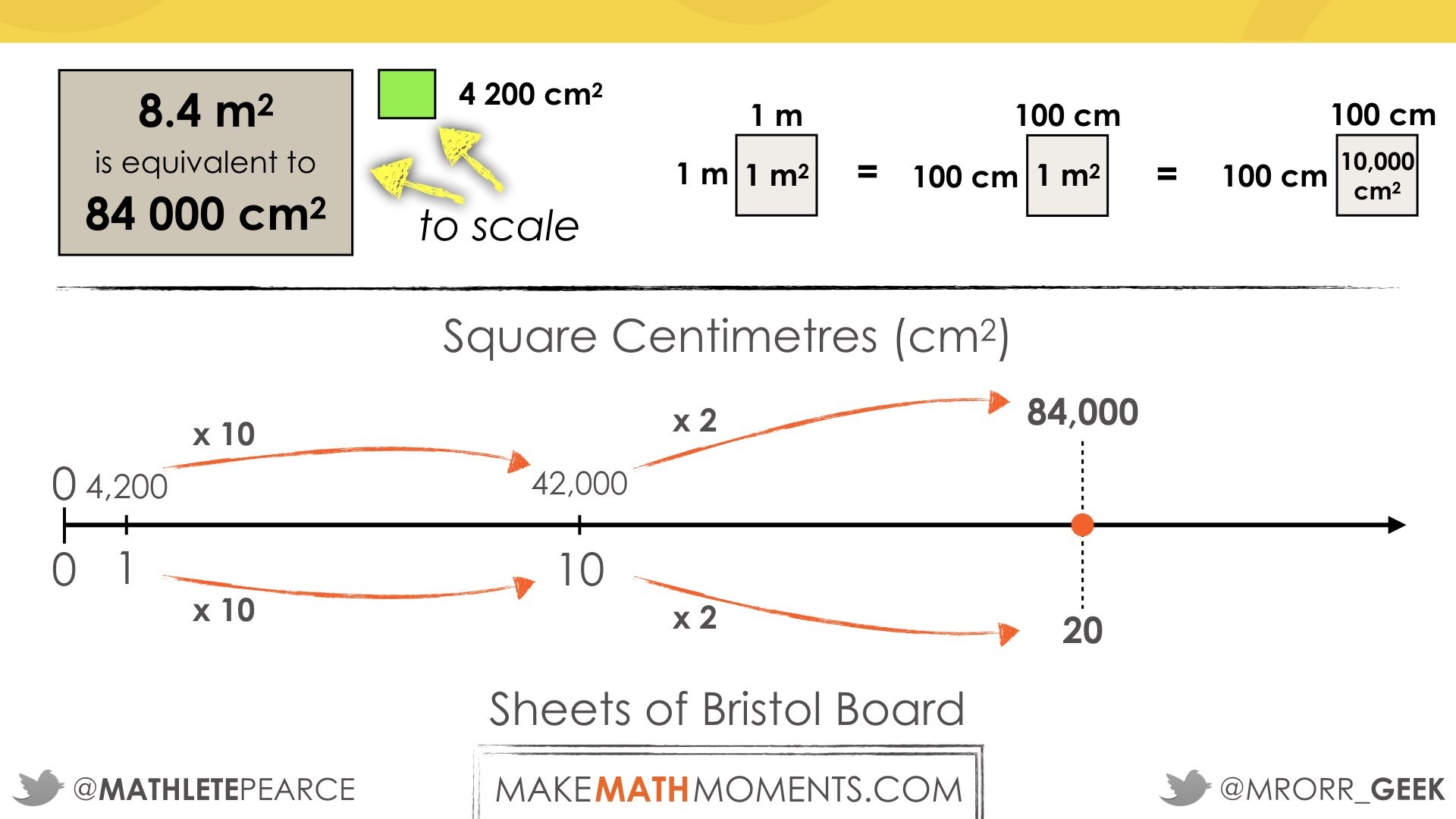
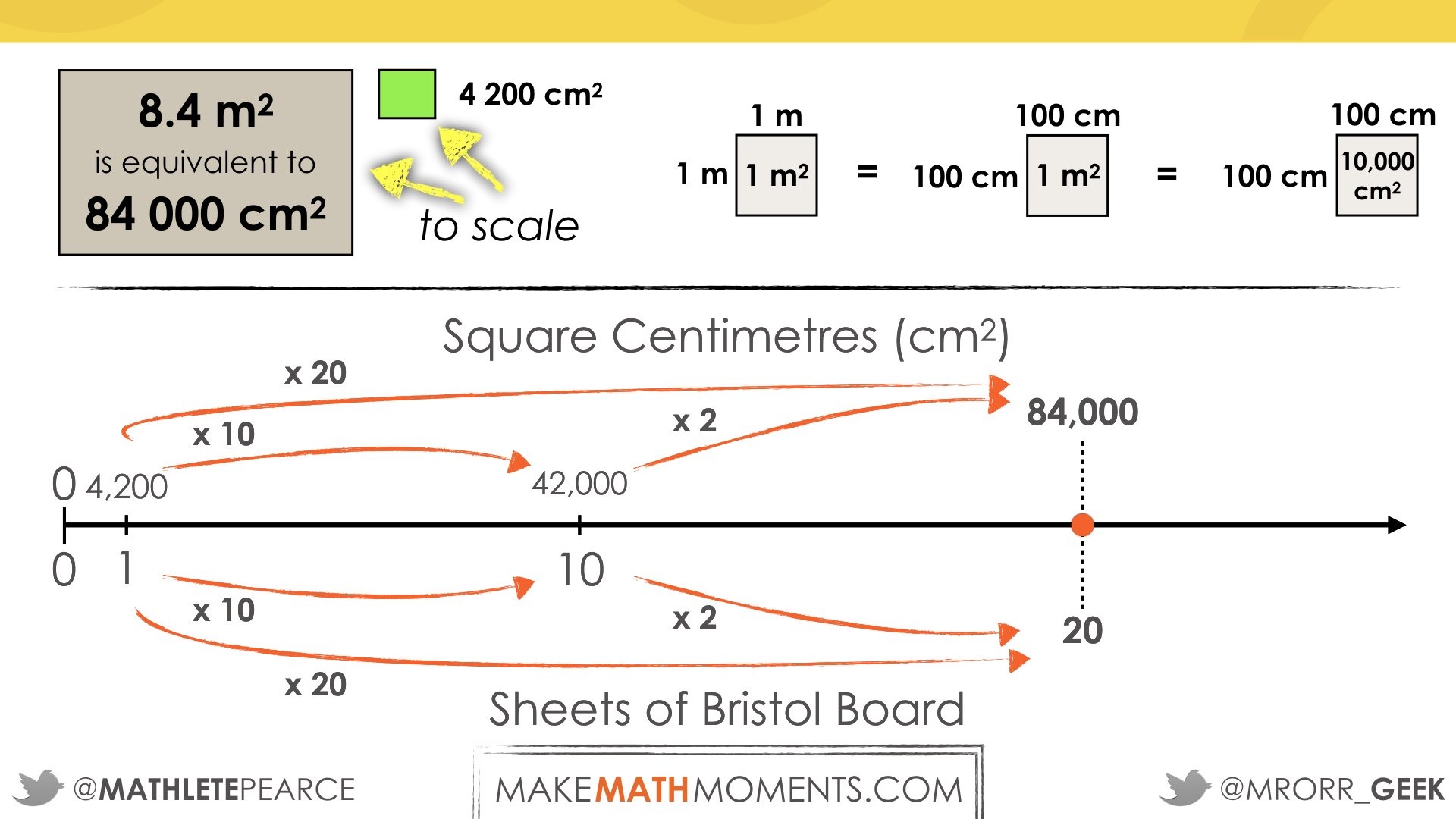
Students may use various strategies that utilize additive thinking (repeatedly adding a single sheet and 4 200 square centimetres, repeatedly adding two sheets and 8 400 square centimetres, etc.) or multiplicative thinking (doubling from 1 sheet and 4 200 square centimetres to 2 sheets and 8 400 square centimetres to 4 sheets and 16 800 square centimetres, etc.), or they may determine the scale factor utilizing quotative division:
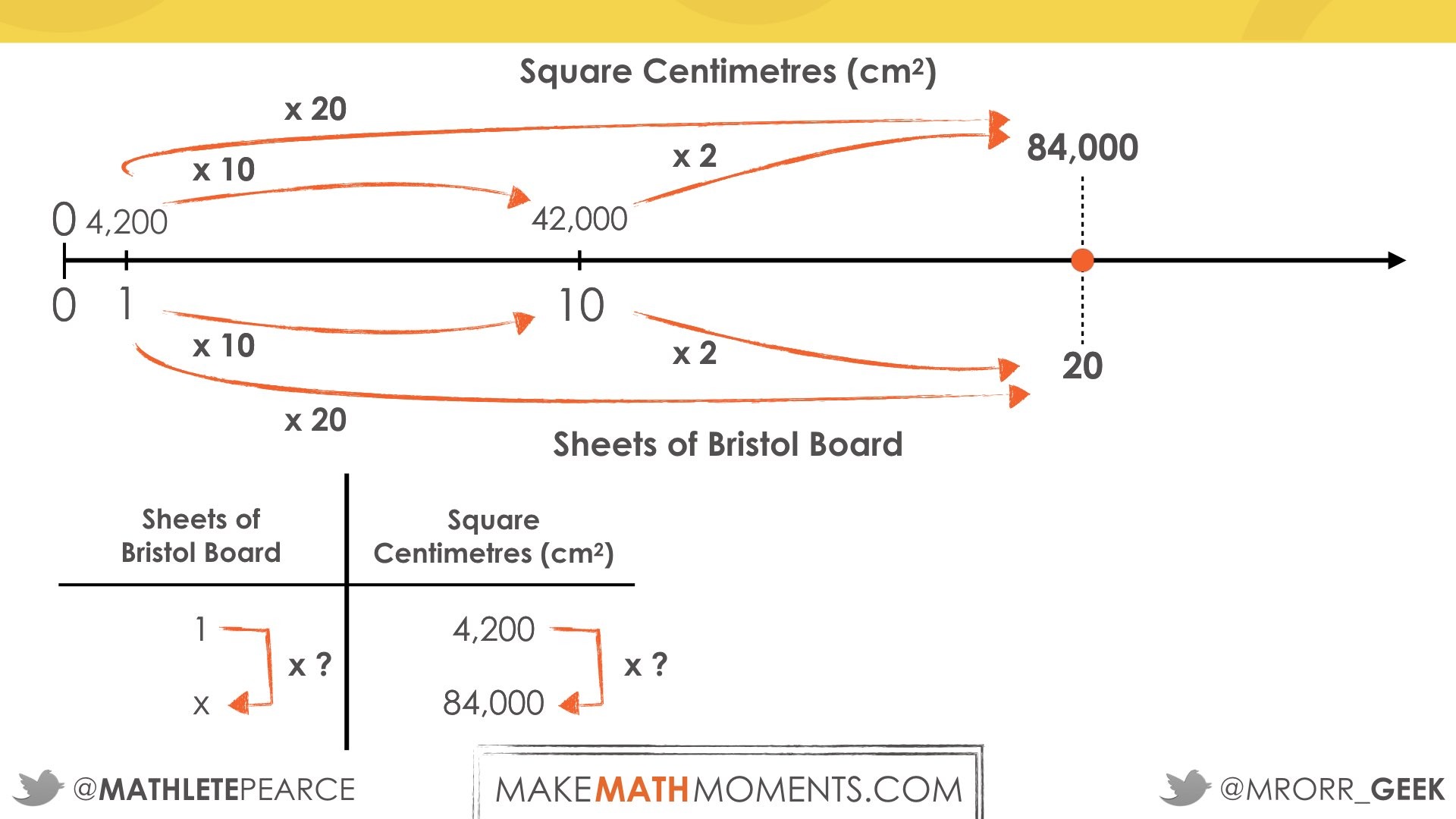
Student Approach #2: Scaling In Tandem With A Ratio Table
Students use a ratio table to scale in tandem:
Sample Response #3
Students set up a proportion using equivalent ratios from the double number line and/or ratio table by writing the ratios using a fraction bar:
It should be noted that when we take two equivalent ratios and write them as a proportion using the fraction bar, we are in the “process” of revealing two equivalent rates. Learn more about this in The Concept Holding Your Students Back course.
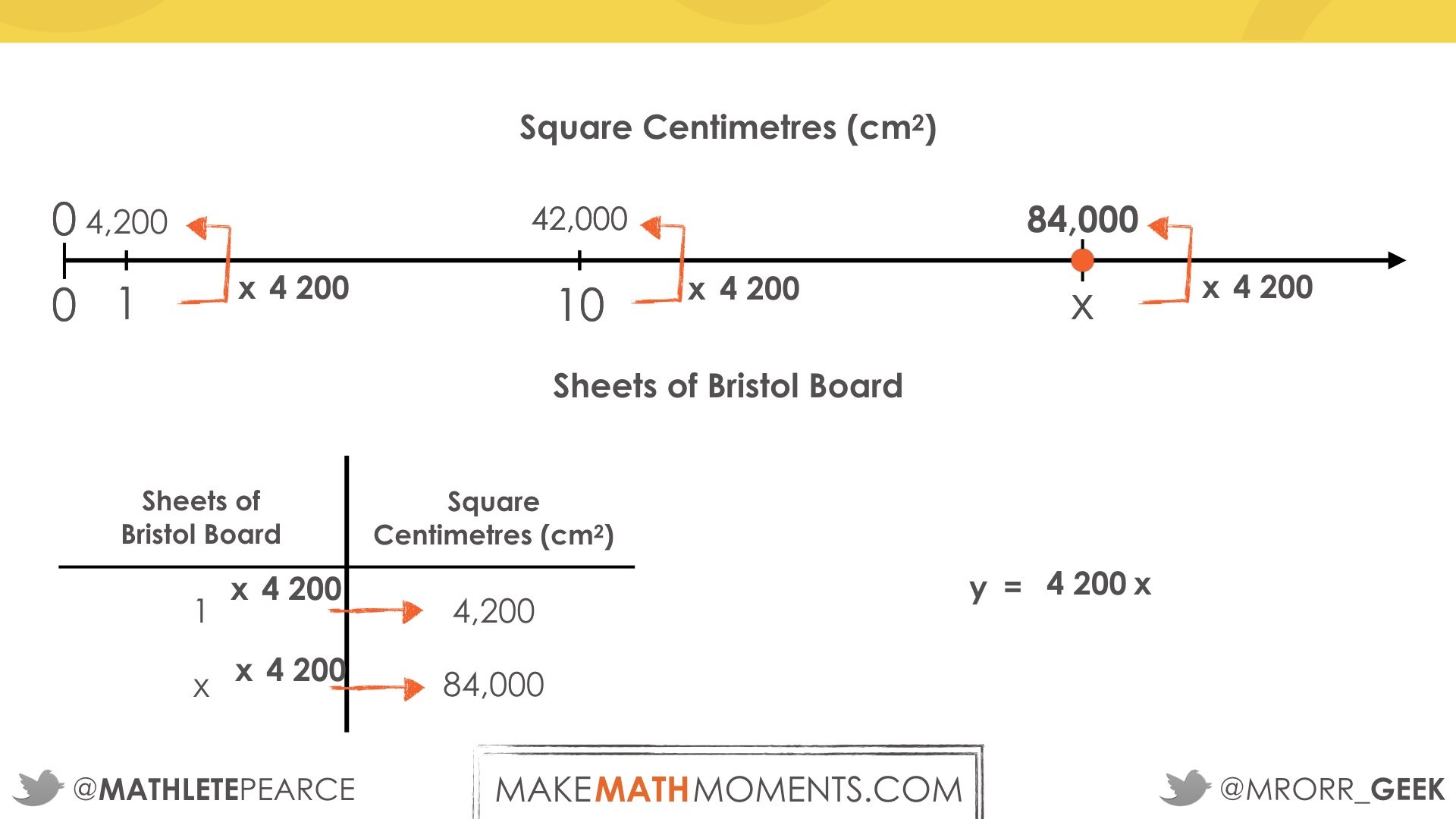
Student Approach #4: Rate Reasoning With A Double Number Line
Students use partitive division across the double number line or ratio table to reveal a rate of how many square centimetres per sheet or how many sheets per square centimetre.
Partitive division 4 200 square centimetres divided by 1 sheet = 4 200 square centimetres per sheet:
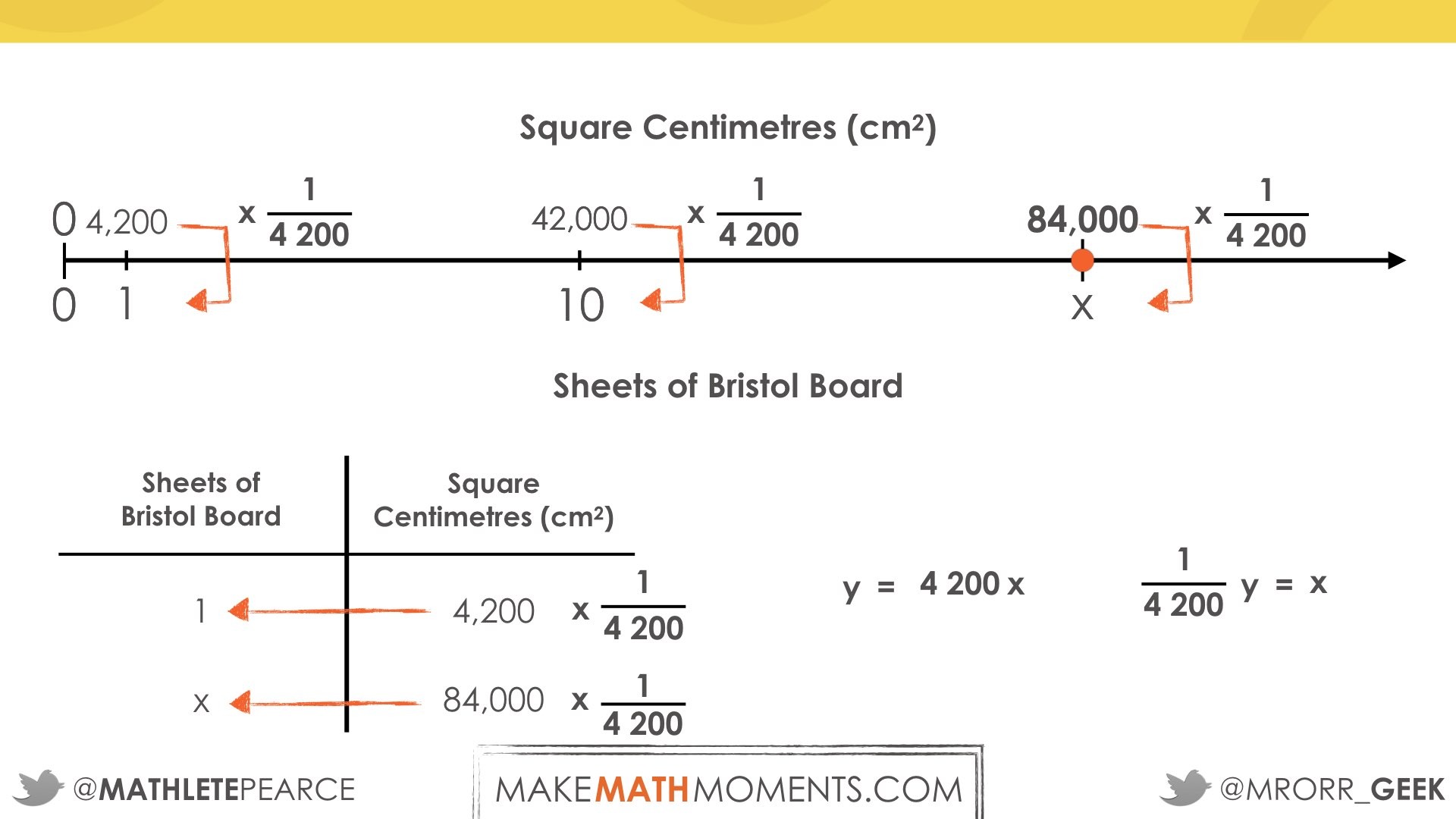
Using Partitive division of 1 sheet divided by 4 200 square centimetres = 1/4200 sheets per square centimetre:
Student Approach #5: Operational Sense Symbolically
Students utilize operational sense to scale up and down converting units as well as determining the number of sheets required to cover the wall:
Next Moves
Reveal
After consolidating learning using student generated solution strategies and by extending their thinking intentionally, we can share what really happened with this video.Revisit the student answers. Have students discuss their thinking and what they would change if they did the task again.
Return to the questions you recorded from your list of student Noticing and Wondering and answer any questions that have not been answered.
Consolidation
In this task, students are challenged to think proportionally as they compare the area of one sheet of Bristol board to the area of the entire wall.
With this, students are able to access the task using additive thinking or multiplicative thinking with ratio or rate reasoning.
In Student Approach #1, students are using multiplicative thinking with ratio reasoning as they scale the composed unit of total area in square-centimetres to Bristol board sheets from 4,200 square-centimeters to 1 Bristol board sheet and doubling repeatedly until getting close to the total of 84,000 square-centimeters.
Modelling this on a double number line and in a ratio table can be helpful as you consolidate student generated solution strategies during the consolidation to help students notice and name the composed unit they are scaling up.
You can see similar examples in student approaches 2 and 3 as well.
When we get to student apporaches 4 and 5, these students are leveraging rate reasoning by revealing the constant of proportionality (or rate) of 4,200 square-centimeters per sheet and simply using that rate to divide 84,000 square-centimeters by the rate to reveal the total number of sheets.
It is common for us as math educators to rush to rate reasoning because it is a quick and efficient method, however students must build their ratio reasoning skills in order for their rate reasoning skills to develop.
Reflect and Consolidation Prompts
Some extension questions you might consider using to incorporate additional purposeful practice and exploration based on the same context:
Extension #1
How many sheets of Bristol board would be needed to cover a wall with an area of 42 square metres?
Extension #2
How many sheets of Bristol board would be needed to cover all four walls of the gym with a length of 28 m, width of 18 m, and height of 14 m?
Extension #3
The school has 62 sheets of green Bristol board in the stock room. How many classes can build their own green screen if each class green screen must cover an area of 6.72 m?
If Students Struggle, You Could…
- …modify the quantities from 8.4 square metres to 8 square metres and 4 200 square centimetres to 5 000 square centimetres and ask students to represent using square tiles or similar a concrete model.
- …ask students to represent using grid paper where each square represents 1 square metre and shading each square for each piece of Bristol board.
Assessment For Learning
We should always be engaging in formative assessment through observations, conversations, and student product.
Be sure to watch for:
- students who are able to clearly represent why 1 square metre is equivalent to 10 000 square centimetres. When students are able to articulate why the 1:10 000 ratio of square metres to square centimetres exists, they are demonstrating fluency with proportional reasoning and they will likely have less trouble iterating square centimetres up to square metres or partitioning down from square metres to square centimetres.
- students who are able to use their operational sense (similar to Sample Response #4) but are unable to articulate why their strategy works. It is possible that they are still working on communicating their thinking, but it is also possible that they do not have a deep conceptual understanding of why multiplying by 10,000 and dividing by 4 200 produces a correct result. Ask them to explain their thinking including the units of measure associated with each quantity and/or ask them to show their thinking another way.
Resources & Downloads
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!