GOING UP ? - PARKING GARAGE
ADDING AND SUBTRACTING INTEGERS
Represent, describe and solve contextual problems involving addition and subtraction of integers.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview
Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will model addition and subtraction contexts involving positive and negative integers in order to solve various problems.
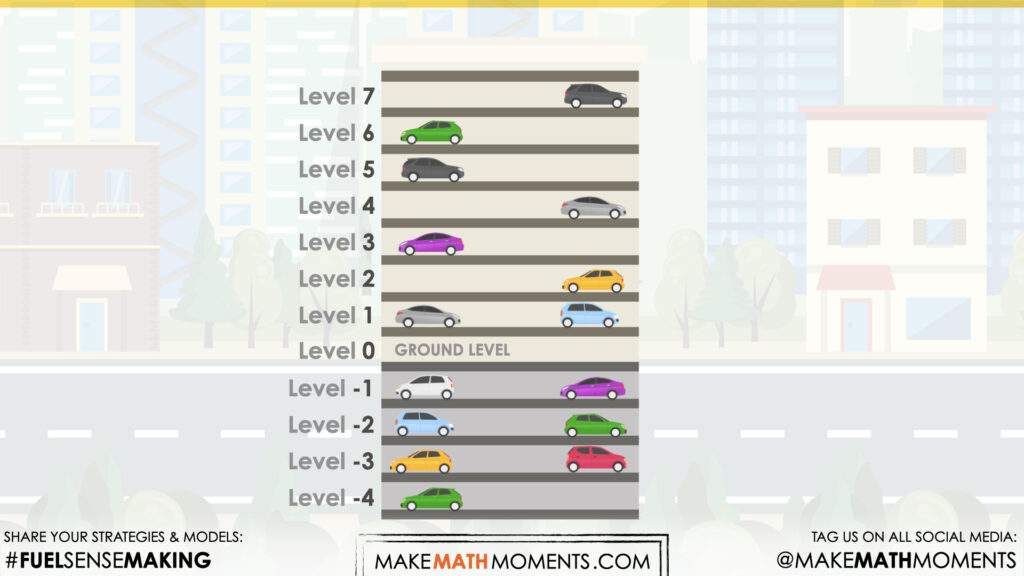
In this task, students will represent the addition and subtraction of positive and negative integers using the context of a parking garage. The scenarios in Day 1 and 2 of this unit will provide the start, the change, and the result will be unknown. Students will describe the position of the car relative to ground level and then add or subtract levels depending on the car’s relocation. They will describe the result of moving the car from one floor to another. Today’s context will create an opportunity to introduce the linear model for solving problems involving negative values. Some of the big ideas revealed in today’s lesson include:
- Situations involving addition and subtraction can be modelled using a number line;
- Integers include zero, all whole numbers and their opposites;
- Integers represented on a number line show their relative distance from zero;
- Some addition and subtraction scenarios follow the structure of start, change and result;
- An integer can represent a change or a quantity;
- When a positive and a negative integer are added together, the result is positive if the absolute value of the positive integer is greater than the absolute value of the negative integer.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group.
Some of the noticing and wondering that came up in a class recently included:
- I notice a street with buildings.
- I notice a large building in the middle.
- I notice there is a car in the building.
- I wonder if it is a parking garage.
- I notice there are twelve levels.
- I wonder why there is a car inside.
- I notice it says ground level.
At this point, you can answer any notices and wonders that you can cross off the list right away. Confirm for students that this building is in fact a parking garage. If it does not emerge through student noticing, ask students to describe the location of the car. For example, the car is three levels below ground level.
Estimation: Prompt
Next, share the following visual prompt briefly and ask the following question:
Each floor in this parking lot is labelled to ensure that all customers can remember where they parked their car. How do you think floors are labelled? Justify your answer.
Estimation: Reveal
Share the following video and or image revealing how the floors in the parking garage have been labelled.
Give students an opportunity to discuss why they may have chosen to label the floors in this way. Point out for students that in this scenario, they are treating the ground level as level 0. All other floors are relative to the ground level.
Fuel Sense-making
Crafting A Productive Struggle:
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common misconceptions;
- most common/frequent to least common/frequent representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Using a pictorial representation.
- Counting.
- Skip Counting.
- Using a linear model to show the change.
- Using a standard algorithm.
Have students share their reasoning for determining the new location of the driver’s car and their equation. Discuss their thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a representation and justification that does not connect to their understanding.
During Moves
While Students Are Productively Struggling….
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Paper folding.
- Using an area model
- Using a bar model
- Using equivalence
- Using common denominators
- Using a symbolic representation.
Have students share their strategies and reasoning for how to determine the fraction of the driveway cleared in the second video. Ask them to convince you and their peers that their answer is correct by sharing mathematical models.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
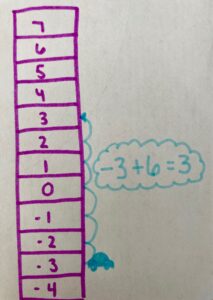
Student Approach #1: Using a Pictorial Representation and Counting
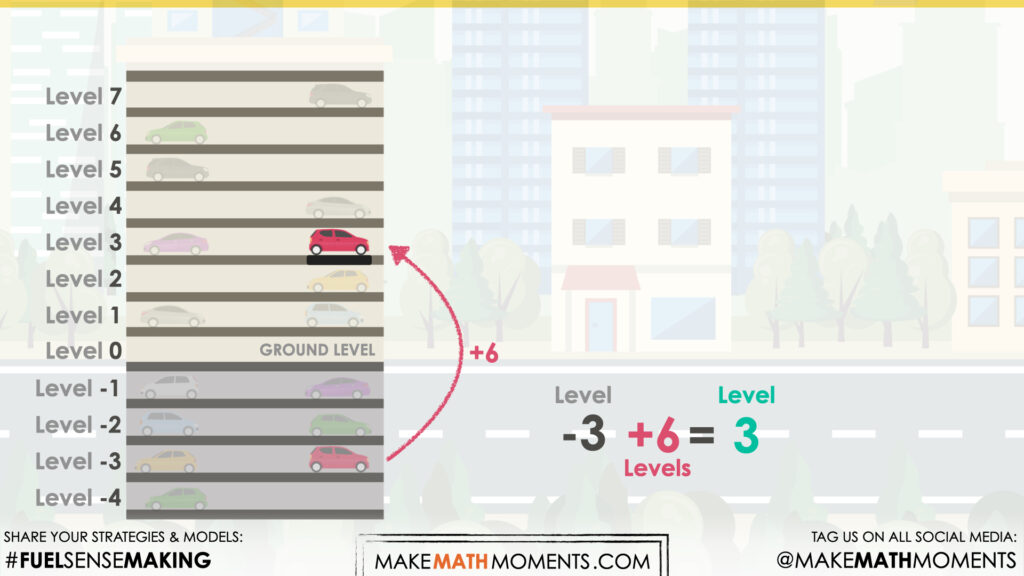
I drew the parking garage. I started on the third floor below ground level and counted up six levels until I arrived at the new location on the third floor. The equation is “start at -3, add 6, and the answer is 3”.
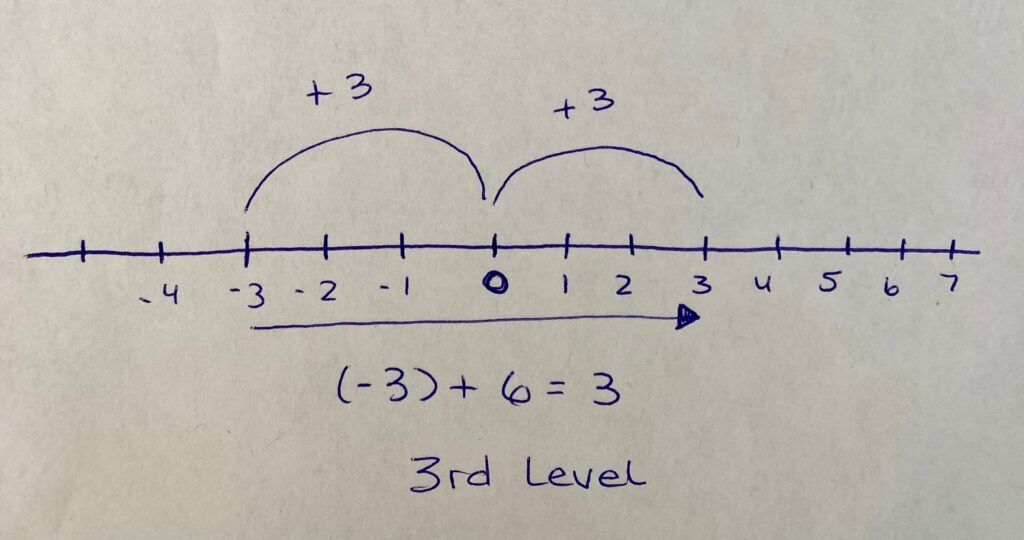
Student Approach #2: Using a Number Line and Reasoning
I drew a number line to represent the parking garage. If the car started on the third floor below zero, I know three floors up is the ground floor, and three more floors would be three floors above, so the third level. The equation is -3, add 6, equals 3.
Next Moves
Consolidation
The big idea in this introductory lesson is to help students see the value of a number line model when operating with positive and negative integers.
We want students to become comfortable with the position of the opposite values relative to zero. Throughout this unit, we will be using the number line to explore different addition and subtraction scenarios and structures.
In this task, we started with a negative value, and added a positive value with
a greater absolute value, which resulted in a positive number.
During the consolidation, explore a few more scenarios that follow this same structure of start – change and unknown result. Encourage students to model and write an equation for each of the following scenarios.
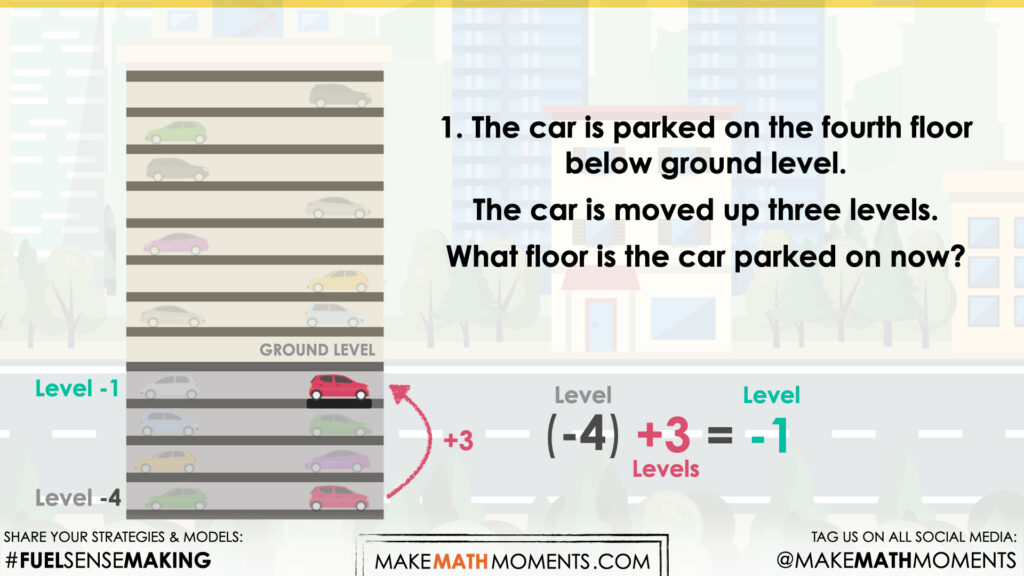
Scenario 1:
The car is parked on the fourth floor below ground level. The car is moved up three levels. What floor is the car parked on now?
Facilitator note:
In this scenario, we are adding a positive value to a negative integer. The absolute value of the positive is less than the absolute value of the negative. The result is negative.
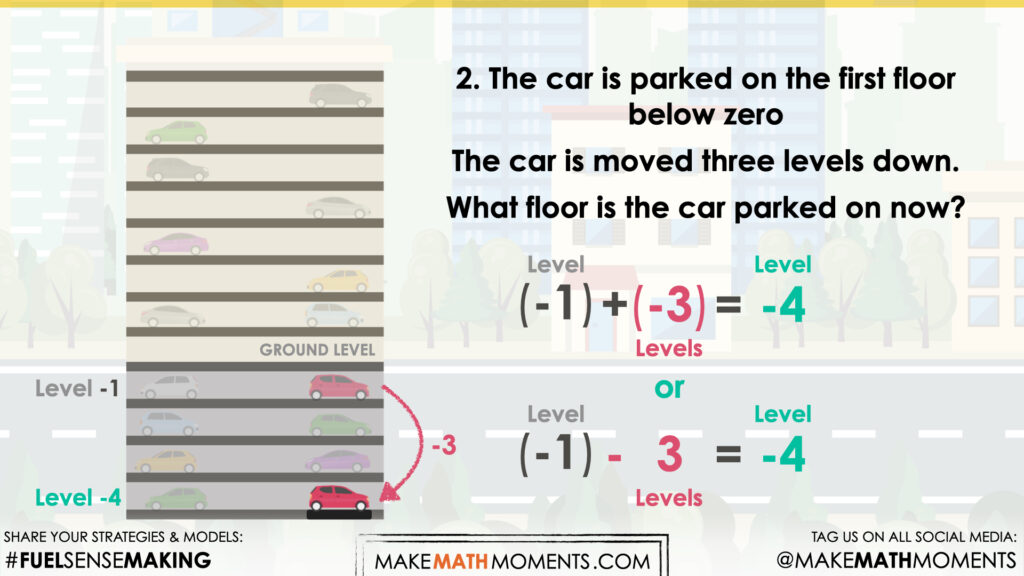
Scenario 2:
The car is parked on the first floor below zero. The car is moved three levels down. Where is the car parked now?
Facilitator note:
The integers in this context can be interpreted as a change or as quantities of floors. For example, if the car starts on the first floor below ground level (-1), and moves down three more floors, this can be expressed as the addition of three floors below [(−1) + (−3)] or as a subtraction of 3 floors (−1 − 3). Both statements result in the same answer (−4).
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
Write two equations that would result in a negative integer.
Write a context for each equation.
Consolidation Prompt #2:
(-2) + (-4) = (-2) – 4
Create a context to defend this statement.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!