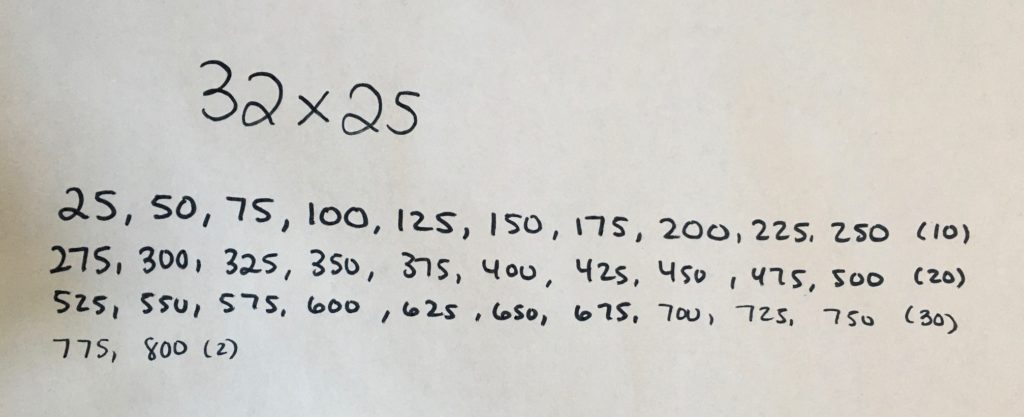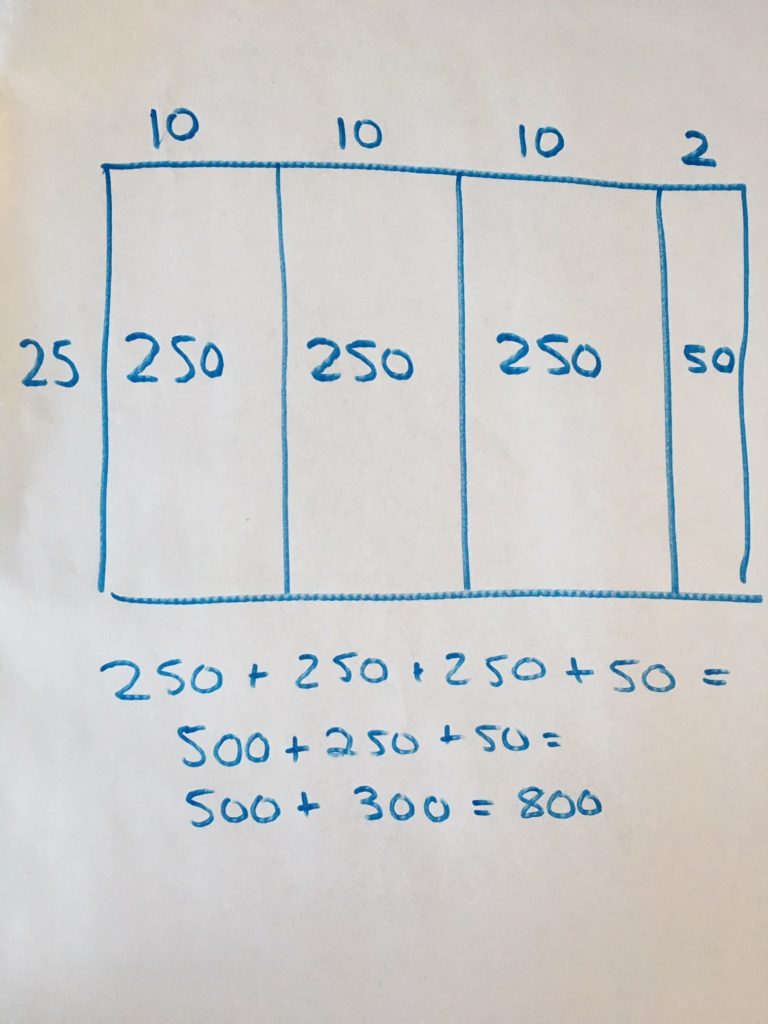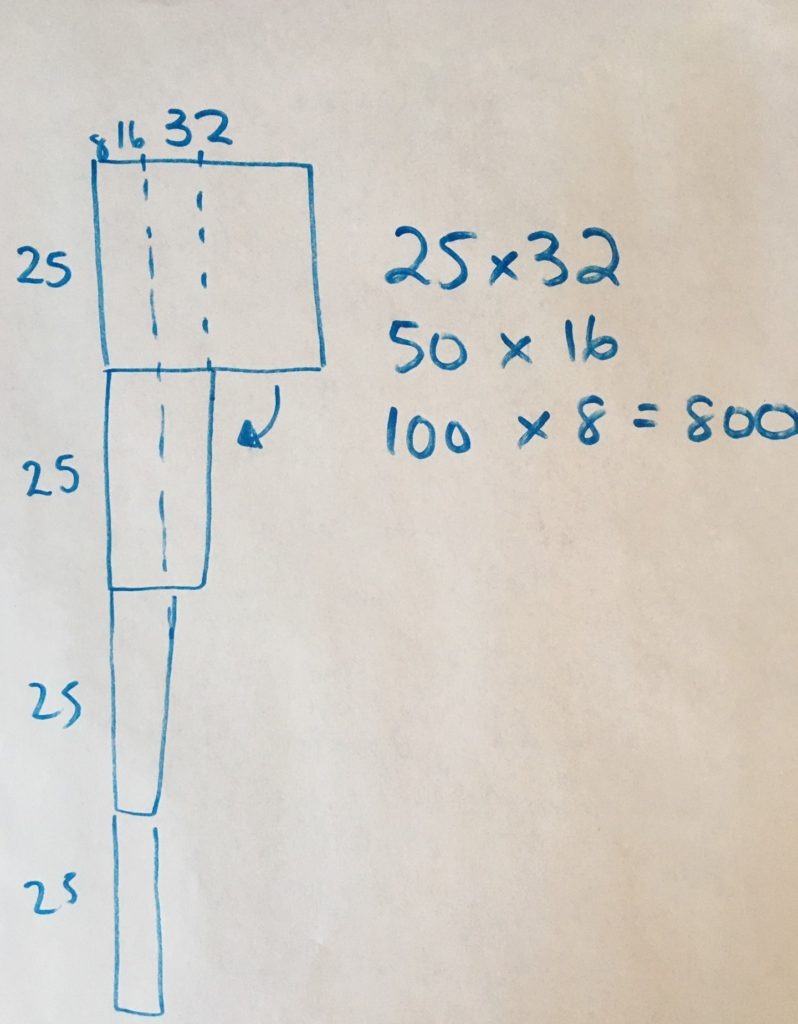DONUT DELIGHT
MULTIPLICATION AND DIVISION
Use arrays to develop and understanding of the relationship between multiplication and division.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview
Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will explore multiplication through the array model.
Intentionality…
In this task, students will determine the number of krispy kreme donuts in a large box given the dimensions of the box in donuts. Students will be multiplying 2-digit by 2-digit numbers without the use of a calculator. The arrangement of donuts in an array might encourage students to use the array model as a tool for determining the number of donuts. Students should be able to use the image in order to defend their calculations. Meaning, if students use a standard algorithm, are they able to see their partial products within the array?
Some of the big ideas that will likely emerge in this task include:
- Creating and/or flexibly redefining the unit (unitizing).
- Repeated additions can be regrouped.
- The relationship between rows and columns in an array.
- Numbers can be composed and decomposed.
- The distributive property of multiplication over addition and over subtraction.
- The associative property of multiplication.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Consider showing students the act 1 video from an episode of Fast Food Mania. The original, longer version is here.
Once the video is complete, show students this image.
Then ask students to do a rapid write of what they notice and what they wonder.
Students will then share out their noticings and wonderings while the teacher writes their ideas down on the whiteboard.
Some noticings and wonderings that have come up when I’ve used the task with the huge box of donuts include:
- How many donuts are in that box?
- How heavy is the box?
- Those people look really small.
- Is this a real picture?
- How many calories are in that box?
For those who wish to go there and extend the discussion around the noticing and wondering, you can check out this article that covers the event at which this donut box was prepared for.
While you might explore some other wonderings, the first question we intend to address is:
How many donuts are in that box?
With manipulatives and/or paper/whiteboards already out on their tables, I would then give students some time to make an estimate and discuss with their neighbours and/or group.
Encourage students to consider a number that they know is for sure too low, one that is definitely too high, and ultimately land on their best estimate and share out.
After students have shared out their estimates, give them more information so that they can make their answer more precise.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Now, share out the following image:
Follow up with:
Update your estimate.
How might we convince someone that the quantity you come up with is reasonable without the use of a calculator?
Students have now been given enough information to now make calculations using mental math to improve their estimates based on spatial reasoning and/or prior knowledge.
Students may work with a partner or in a small group to determine the number of donuts in the box, however they will do so without the use of a calculator. They must also be able to convince others of how their answer is true.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Base ten materials
- Square tiles or linking cubes
- Drawings
- Arrays and/or area models
- Symbolic including but not limited to a standard algorithm and a flexible algorithm using partial products.
Have students share their strategies and reasoning for determining the total number of donuts.
Ask them to convince you and their peers that their answer is correct by sharing mathematical models.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
Student Approach #1: Skip Counting
I saw from the pictures that there are 32 columns of 25 donuts. I also know how to count by 25, that’s easy, it’s like counting quarters when you are counting money. I started counting b by 25s, but I realized I need to find a way to keep track of how many 25s I had counted. So I would count to ten 250s, and then start a new row. Once I counted by 25 thirty-two times, the answer was 800 donuts.
Approach:
This student used skip counting to access this task.
Student Approach #2: Distributive Property With An Open Array
Since the donuts were already in an array, I decided to use that model. I didn’t want to draw all of the donuts though, because that would take a long time, so I used an open array. I know that the dimensions of the array are 25 by 32, and I think 25 is an easier number to multiply. I decided to leave the 25, and decompose the 32. I know how to multiply by 10, so I broke 32 into 10 + 10 + 10 + 2. I then multiplied each section of the array and added them together.
Approach:
This student used an open array as a tool to make the multiplication more accessible by decomposing one of the factors. Several big ideas are evident in this solution including numbers can be composed and decomposed and the relationship between columns and rows in an array. The distributive property of multiplication over addition is evident in this student’s thinking because they used partial products.
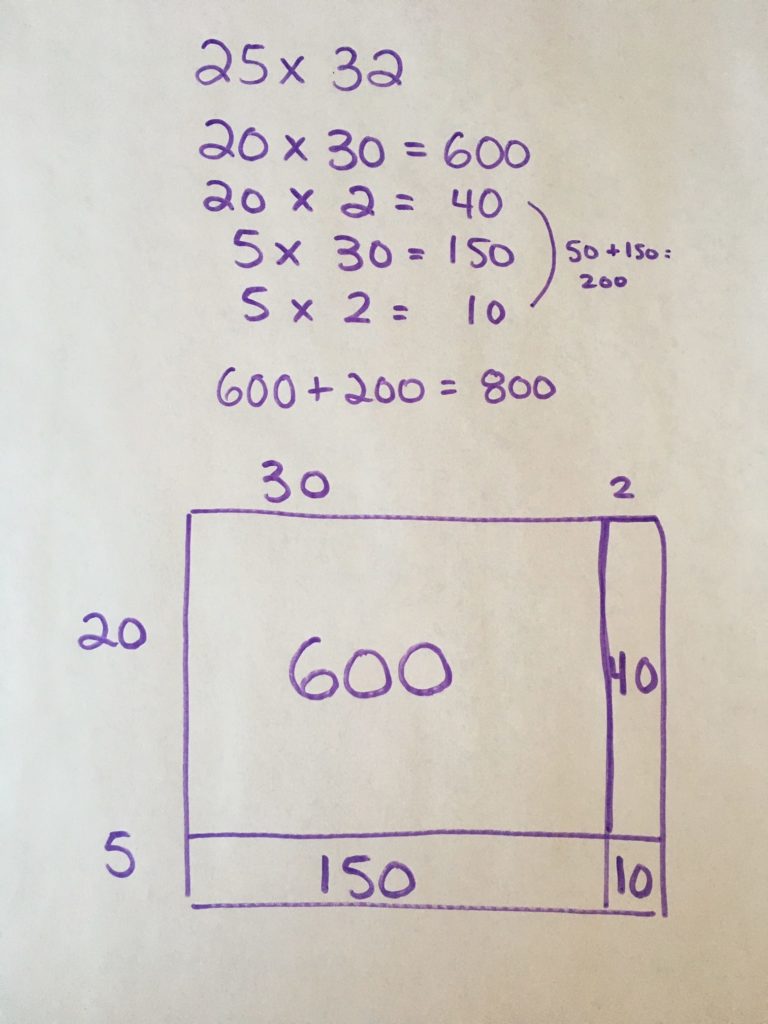
Student Approach #3: Distributive Property With A Symbolic Representation
I know from the picture of the donuts that we have to multiply 25 x 32. So I decided to decompose both numbers using place-value into 20 + 5 and 30 + 2. Then I knew I had to multiply 20 and 5 by both 30 and 2. I found the products and then added them together. I used the open array below just to show why my strategy works.
Approach:
This approach is similar to the student sample above, however this student used a symbolic representation and then used the open array to represent their thinking. Unlike the previous example, this student decomposed both factors (rather than only one of the factors) and used the distributive property of multiplication over addition to find partial products and then added them together.
Student Approach #4: Doubling and Halving With An Open Array
I looked at the array and thought, 32 is not a very friendly number. So I wonder, could I decompose and rearrange the array? I decided to cut the columns in half, and move them below. So now I have a box that is 50 donuts by 16 donuts. Still not that friendly, so I did it again, I split the columns in half and moved them down again. Now I have a box that’s 100 donuts by 8 donuts, I know that’s 800 donuts.
Approach:
This student used the array as a tool to make sense of their doubling and halving</b strategy. They used the associative property of multiplication. In reality (although not evident yet in their thinking), they decomposed the 16 into 8 x 2, and re-associated the 2 with the 25 to make 50. They repeated this same process again to make 100 donuts x 8 donuts, a friendly fact to work with.
Next Moves
Reveal
After the consolidation of learning is complete, you might consider sharing the following animation that reveals a few common approaches using some important mathematical models and strategies:
Consolidation
Consolidate learning using student generated solution strategies based on what you selected and how you sequenced while monitoring during the Sense Making portion of the lesson. The purpose of the consolidation is to make connections between strategies and reveal and/or solidify big ideas. In particular, consider highlighting student solutions that leveraged the array model as a tool or as a representation of their thinking.
Consider exploring student strategies that made this multiplication more accessible including the use of partial products or doubling and halving. Model the students justification of all strategies using an array so that the thinking is visual for all learners. Consider using a grid array so that students who might be struggling to see the big ideas can actually see the individual donuts represented as squares on the grid. The grid can actually be cut and recomposed to make the strategy more concrete.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering this consolidation prompt to be completed independently.
Consolidation Prompt:
Lucinda says that she can use an array or area model to make the following multiplication sentence a bit easier. What might her strategy be? Use an array (either concrete, grid or open) to defend your thinking.
25 x 16
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!
