CARD TRICKS
ADDITION STRATEGY: ADD EXTRA AND ADJUST
Dive into this 5-Day Problem Based Math Unit which focused on the efficient strategy of adding extra and adjusting using numbers within 50
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will explore addition in a context encouraging students to use a strategy that allows them to flexibly work with one addend by rounding it to the nearest decade then adjusting after to efficiently add numbers within 50
Intentionality…
In this task, students will engage in an addition context and lead towards the “Add extra and adjust” strategy.
Some of the big ideas that may emerge through this task include:
- Understanding hierarchical inclusion allows for flexible composing and decomposing of numbers
- Numbers can be decomposed by separating a whole into two or more parts
- Addition names the whole in terms of the parts
- Different addition situations will elicit different strategies
- Number relationships provide the foundation for strategies to help students remember basic facts
- Models can be used to connect concrete to abstract
Before starting this unit, students should be familiar with:
- Rounding numbers
- Adding decade numbers
- Subtracting near numbers
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following video:
Then, ask students:
What do you notice?
What do you wonder?

Give students about 30-60 seconds to do a rapid write on a piece of paper or silent individual think time.
Replaying the video can be helpful here if appropriate.
Then, ask students to pair share with their neighbours for another 60 seconds.
Finally, allow students to individually share with the entire group. Be sure to write down these noticings and wonderings on the blackboard/whiteboard, chart paper, or some other way that is visible to all. This helps students to see the thinking of their classmates and ensures each student that their voice is acknowledged and appreciated. Adding student names or initials next to their notice/wonder is one way to acknowledge their participation and can motivate others to join in.
Some noticings and wonderings that may come up:
- I notice the magician is putting cards in a hat
- I notice that the magician is taking cards out of the hat
- I wonder how many cards are in the hat.
- I wonder what kind of a trick he is going to do
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Since you have already taken some time to set the context for this problem and student curiosity is already sparked, we have them in a perfect spot to help push their thinking further and fuel sense making.
Share the following video with the prompt.
The magician was organising his magic supplies. He has 33 cards already in the box. He finds another 9 cards so he puts them in the bag too. How many cards does the magician bring with him to do his tricks?

During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Educators are looking for students that are making their thinking visible so it can be displayed during consolidation. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common misconceptions;
- most common/frequent to least common/frequent representations; or,
- choose another approach to selecting and sequencing student work.
The strategies you might see students use include:
- Direct model and counting all
- Counting on
- Algorithm
- Efficiently break apart one number
- Add Extra and Adjust
Assessment:
This checklist can be used for tracking formative assessment as students are working. The information collected can be used to form whole group, small group or one-to-one support models.
Early strategy | Direct modeling and counting all | Students will count the initial value, count the amount added then count all of the amounts. Example: Count 1: 7 blocks Count 2: 4 blocks Count 3: 7 blocks and the 4 blocks to know 11 blocks in all |
Pre-cursor skill | Count On | Students are holding one number in their head and continuing to count forward and track their count |
Add 10 on the decade | This skill demonstrates student understanding of place value. By mentally adding 10 (or 20, 30, 40, etc) from a number, students will only need to adjust the tens column (or possibly the hundreds column as the numbers get bigger). Can students do this without counting on 10? | |
Add 10 off the decade | This skill is similar to adding 10 on the decade but the starting number will not be a number that ends in zero (e.g. 23, 34, 41, 56, etc). Again students are using place value to adjust the tens column (or possibly the hundreds column as the numbers get bigger). Can students do this without counting on 10? | |
Break apart one number into easier pieces | This strategy extends beyond the teen numbers though. One of the numbers (ideally the smaller number) is broken into parts (decomposed) that will make it easier to add. E.g. 34 + 18 We would keep 34 whole and decompose 18. The decomposition is not random. We want students to work with decade numbers and add on. 6 can be decomposed from 18 34 + 6 = 40. By getting our number to 40, we have made it easier to add on the remaining parts. Students may be able to add on the remaining 12 from the 18 in one move or they may choose to decompose 12 as well. Regardless, we want to eliminate the counting on strategy and instead start working with numbers. 40 + 12 = 52 Therefore 34 + 18 = 52. | |
Strategic and efficient strategy: Add Extra and Adjust | In the Add Extra and Adjust strategy, students round one addend to the closest decade number first and then add that amount. For example, 34 + 19 can be mentally solved by adding 20 first (34 + 20 = 54). Now an adjustment needs to be made because too many were added, so 1 more needs to be subtracted. 54 – 1 = 53. Therefore 34 + 19 = 53. | |
Student Approaches
Student Approach #1: Counting All with a Drawing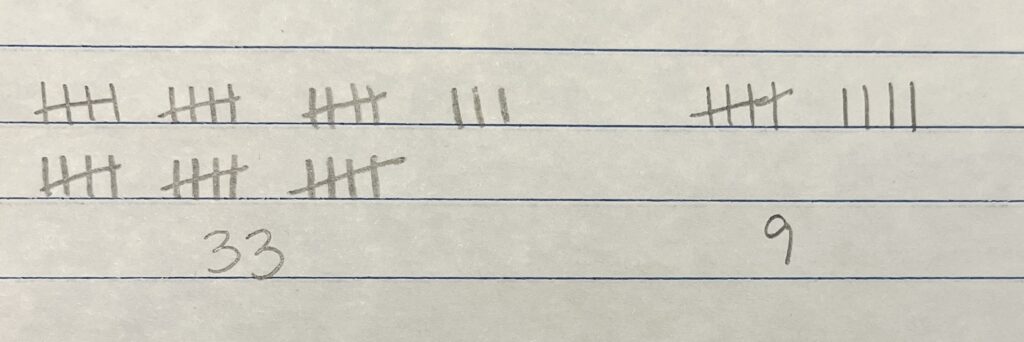
I drew 33 tallies for the 33 cards. I drew 9 more tallies and then counted all of them. There were 42 tallies so the magician needed 42 cards for his tricks.
Student Approach #2: Counting On
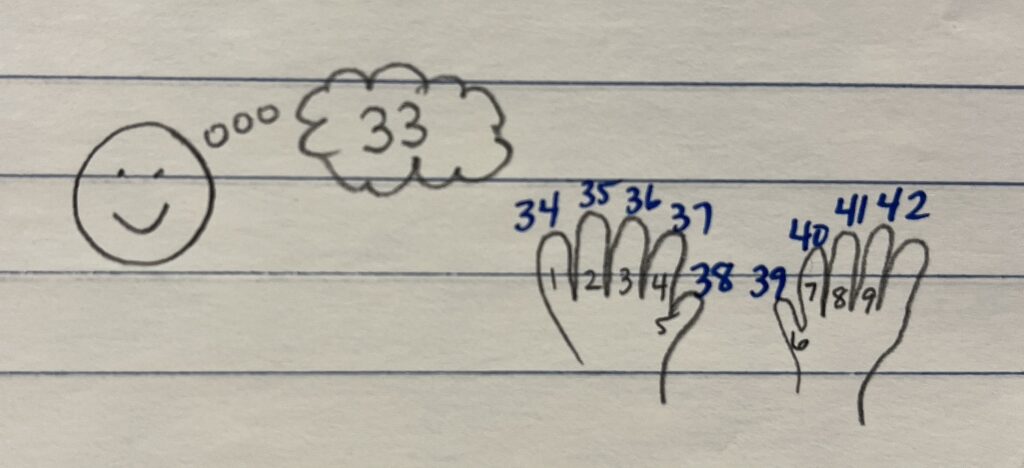
I thought about 33 in my head and then counted on 9 keeping track on my fingers.
Student Approach #3: Algorithm
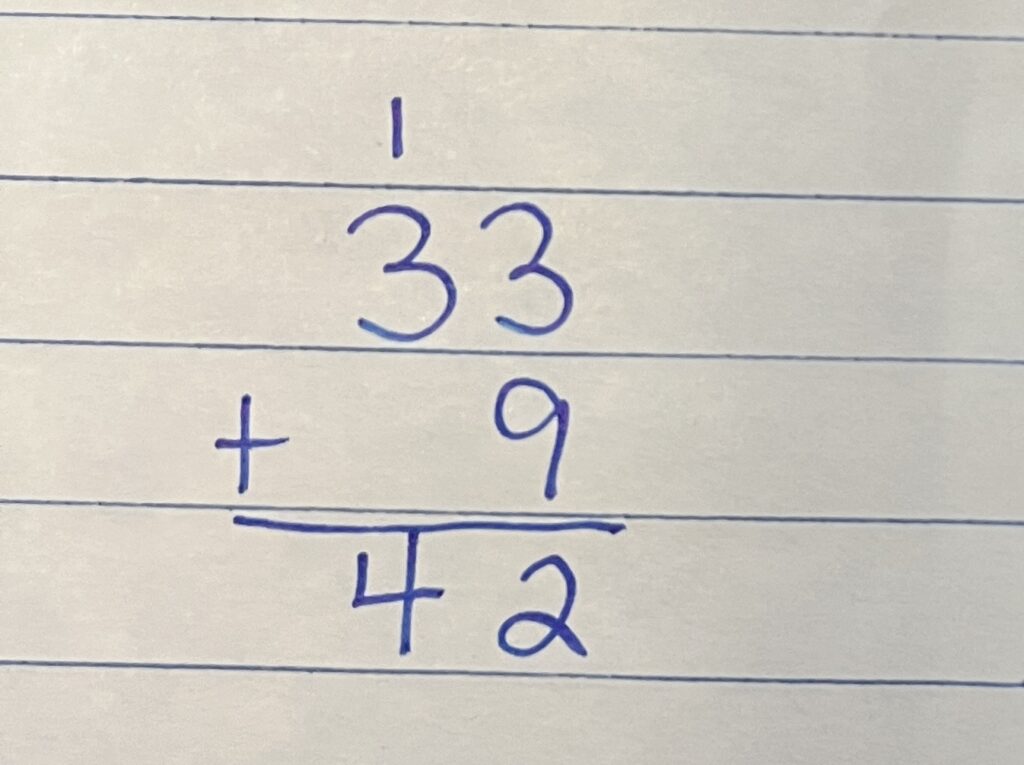
I stacked 33 and 9. I first added 3 and 9 to get 12. I put down the 2 and carried the 1 which is 10. So I added 3 and 1 to get 4 or forty. So there are 42 cards.
Student Approach #4: Efficiently Break Apart One Number
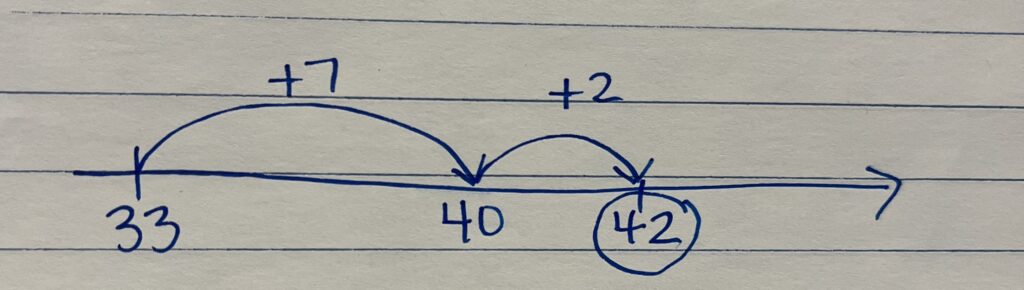
I started with 33 and first added 7 to get 40. Then I added 2 more to get 42.
Student Approach #5: Add Extra and Adjust
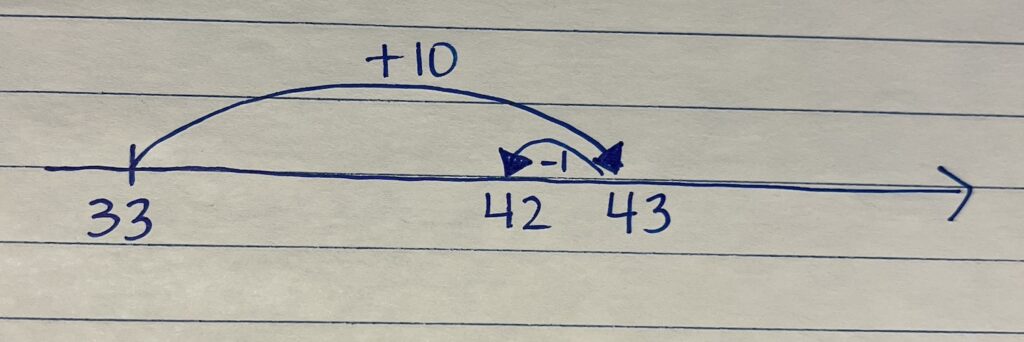
Instead of adding 9, I added 10. So I used 33 + 10 = 43. But I added too much so I need to take one away. So the answer is 42.
Next Moves
Reveal
Show students the following reveal video:
Reveal 1:



Reveal 2:

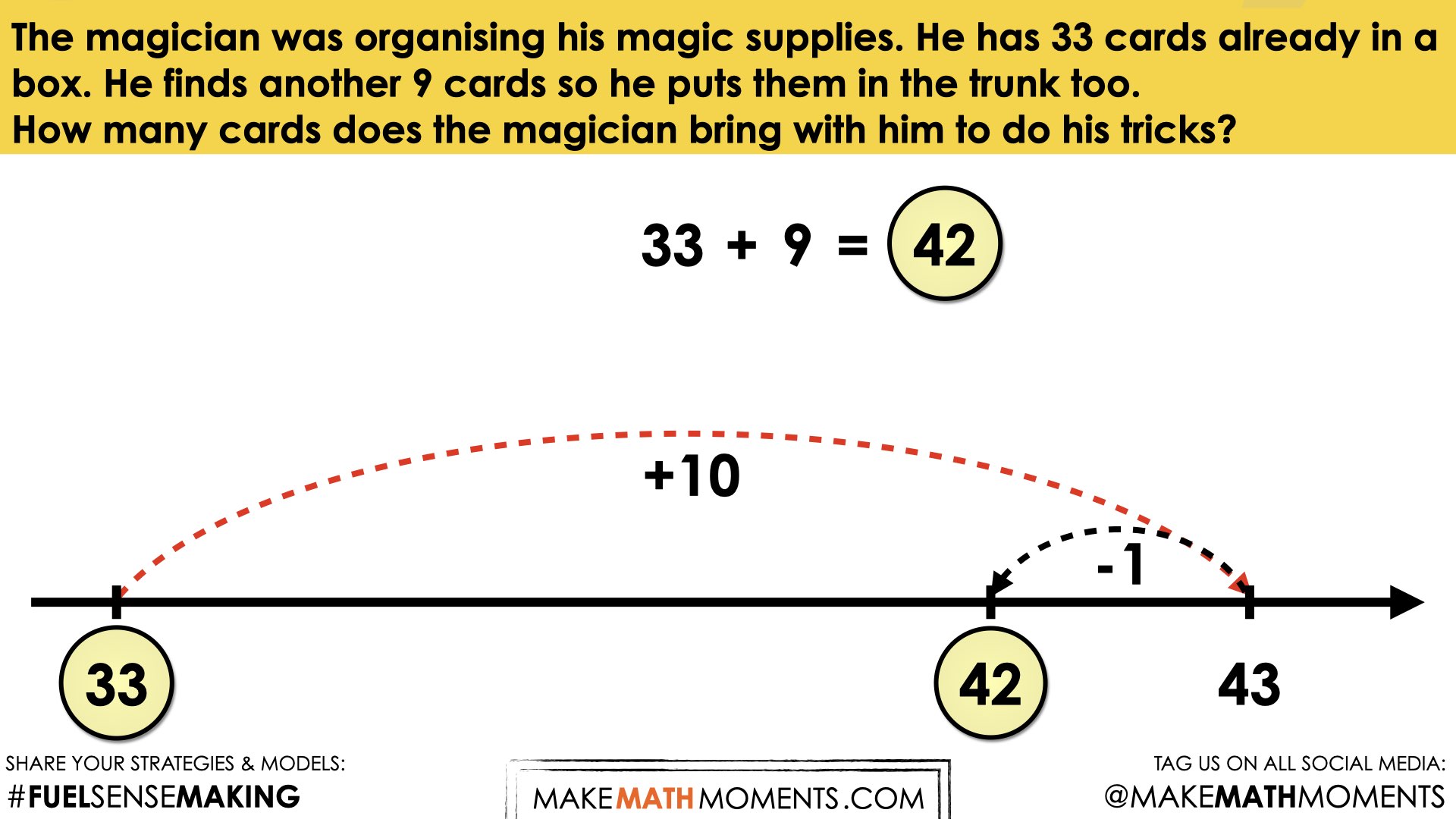
Facilitator Note:
The open number line (or empty number line) is an incredible tool for students to use to demonstrate their thinking. It allows flexibility from the traditional number line because students do not have to count the “ticks’ or “spaces”, instead they may jot their thinking anywhere on the line.

Consolidation
Consolidate learning by facilitating a student discussion.
The goal of the consolation is to demonstrate the flexible way that we can add an easier number by rounding one of the addends and adjusting. In the “Add Extra and Adjust” strategy, students round one added (the number being addend) to the closest decade number first and then add that amount. This is an effective strategy when one addend is close to a decade number (e,g., 8, 9, 18, 19, etc). By adding 10 or 20 in any of these cases, the students are eliminating the need to count on and are instead working with the numbers.
In both of these examples, too much has been added so an adjustment needs to be made to compensate for that.
In this question, only 9 was supposed to be added. Since 10 was added instead, that was 1 too many. Therefore, 1 needed to be subtracted to adjust for the “over addition”.
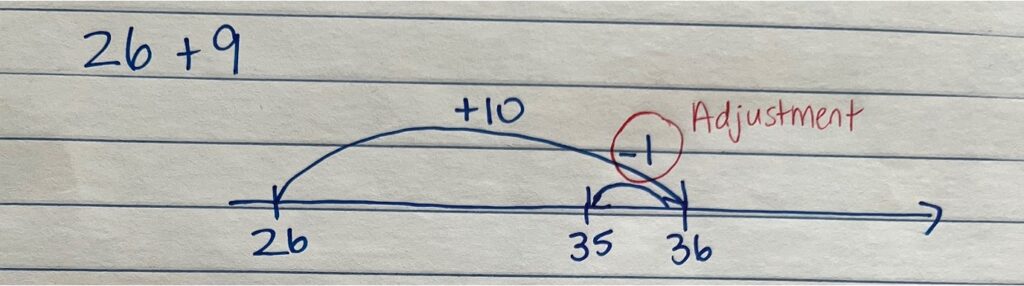
Similarly, this question has an addend of 18. By adding 20 instead, that means 2 too many were added. So in this case, two needed to be subtracted as an adjustment.
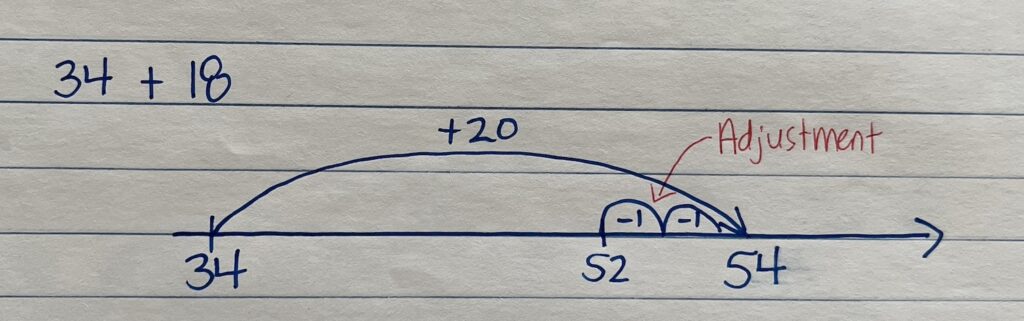
In order for this strategy to be efficient, students need to be able to mentally add 10 (or 20, 30, 40, etc) to a number without having to count on. Students who struggle with this may need further place value support. Students that are counting on often “get lost” as they have to travel over a decade. As the numbers get higher or the count on becomes larger, counting is not always as reliable. There are too many pieces for a student to keep track of.
This problem may become more obvious by modelling the thinking on an open number line. It will allow students the opportunity to see that we have added too much so that is why subtraction needs to be used as an adjustment.
We want students to start feeling more comfortable with adding numbers in a way that makes sense to them rather than just counting.
During the discussion, encourage students to start by showing their work without an explanation. Classmates will use this time to understand the visual and make their own assumptions about the work in front of them. It is also an option to ask students “What do you think this group did to solve this question?”. This will engage students in the work. The group can clarify any misunderstandings.
Reflect and Consolidation Prompts
Add Extra and Adjust is an effective way to add. It is important for students to understand when to use a strategy rather than just relying on their favourite strategy. In this case, this strategy is most effective when one addend is just under the decade (8, 9, 18, 19, etc). In each, it is easier to mentally add the decade number and adjust to get the answer. Support may be needed for students to recognize how they need to adjust after rounding the addend. Sometimes students may continue adding. The following picture shows a common mistake. The first number line shows the student adding one more after adding 10. The bottom number line shows the correct idea that too much was added so the real answer is one lower.
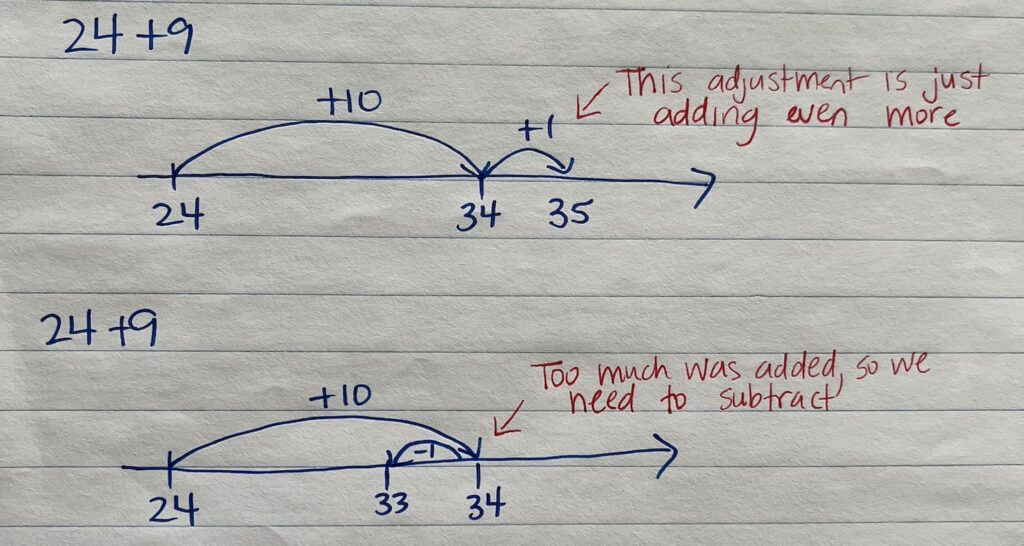
Consider the strategies that the students used. Perhaps a review of adding off the decade is necessary (e.g., 23 + 10, 34 + 20, 56 + 20, etc).
Provide students an opportunity to reflect on their learning by offering these consolidation prompts.
Consolidation Prompt #1:
How is adding 10 or 20 to a number easier than adding 9 or 19?
Consolidation Prompt #2:
36 + 19
Show your thinking on a numberline.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!




