TAKE A CHANCE [DAY 4]
PROBABILITY OF A CHANCE EVENT
Express the probability of a chance event.
Intentionality
Math Talk
Visual Math Talk Prompt #1
Purposeful Practice
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview
![Take a Chance [Day 1] | Data: Probability 3 Act Math Task](https://learn.makemathmoments.com/wp-content/uploads/2024/03/MMM-Task-Take-a-Chance-Featured-Image.png)
Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will continue expressing the probability of a chance event as a fraction on a probability line.
Intentionality…
The purpose of the Day 4 activities is to reinforce key concepts from Days 1- 3. Students will engage in a math talk and have an opportunity to complete independent purposeful practice. The math talk and purposeful practice serve to develop a deeper understanding of the following big ideas:
- Fractions can express the probability of a chance event.
- The theoretical probability of a chance event is a number between 0 and 1, representing the likeliness of the event occurring.
- Numbers close to 1 indicate greater likelihood, while a probability near 0 indicates an unlikely event.
- The theoretical probability of a chance event can be used to predict the likeliness of that event.
- The more trials done in an experiment, the closer the experimental probability will be to the theoretical probability.
Math Talk
During today’s math talk, we will continue exploring how theoretical probability can be leveraged to predict chance events. In today’s context, ten tiles are placed in a bag. One tile is pulled at random. This experiment is repeated 200 times. Students are asked to predict how many times a vowel will be pulled from the bag.
Visual Math Talk Prompt #1


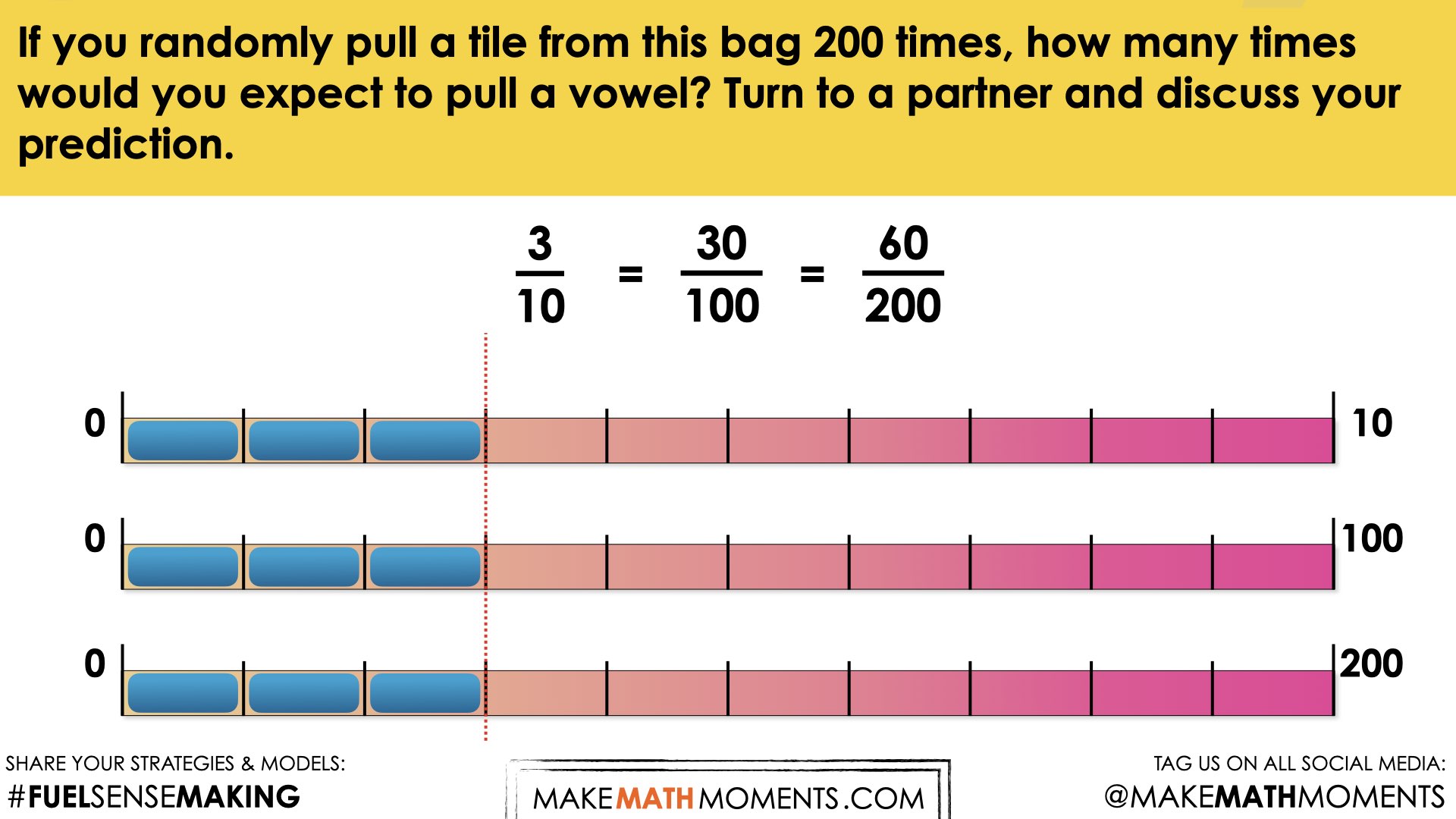 Student prompt:
If you randomly pull a tile from this bag 200 times, how many times would you expect to pull a vowel? Turn to a partner and discuss your prediction.
Facilitator note:
Students should consider that 3 of ten tiles are vowels. This helps us predict that three-tenths of the random pulls will result in a vowel. Support students in understanding that scaling is helpful when the number of pulls increases. For example, if 3 out of 10 pulls result in a vowel, then 30 out of 100 pulls result in a vowel, and 60 out of 200 pulls would be a vowel. The 3/10 relationship remains.
Student prompt:
If you randomly pull a tile from this bag 200 times, how many times would you expect to pull a vowel? Turn to a partner and discuss your prediction.
Facilitator note:
Students should consider that 3 of ten tiles are vowels. This helps us predict that three-tenths of the random pulls will result in a vowel. Support students in understanding that scaling is helpful when the number of pulls increases. For example, if 3 out of 10 pulls result in a vowel, then 30 out of 100 pulls result in a vowel, and 60 out of 200 pulls would be a vowel. The 3/10 relationship remains. Purposeful Practice
While Students Are Practicing…
Login/Join to access the entire Visual Prompt, downloadable slide decks and printable handouts for this lesson and all problem based units.
Questions: Theoretical and Experimental Probability
Question #1:
Login/Join to access the entire Visual Prompt, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #2:
Login/Join to access the entire Visual Prompt, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #3:
Login/Join to access the entire Visual Prompt, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #4:
Login/Join to access the entire Visual Prompt, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #5:
Login/Join to access the entire Visual Prompt, downloadable slide decks and printable handouts for this lesson and all problem based units.
Resources & Downloads
Login/Join to access the entire Visual Prompt, downloadable slide decks and printable handouts for this lesson and all problem based units.
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Visual Prompt, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!


