THE WOOLY WORM RACE [DAY 5]
FRACTIONS & METRIC UNITS
Represent, compare, order, and add fractions involving metric unit conversions.
Intentionality
Math Talk
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview
Length of Unit: 6 Days
Access each lesson from this unit using the navigation links below
Students will continue developing their ability to represent fractions for the purpose of comparing and converting between fractions, decimals and percents.
Intentionality…
The purpose of the activities we will engage in today are to reinforce key concepts from the previous lessons in this unit and to extend to comparing and converting between fractions, decimals, and percents. Students will engage in a string of related problems through a math talk and will have an opportunity to engage in a rich task that will leverage their ability to represent fractions visually and extend to representing these quantities using the symbolic representations of decimals and percentages. The math talk and tasks student will engage in serve to develop a deeper understanding of the following big ideas:
Number:
- Fractions can be represented in a variety of ways;
- How you partition the whole determines the fractional unit (i.e.: partitioning a whole into 6 parts will result in 6 sixth parts);
- As you partition a whole into more parts, the smaller the size of each part;
- As you partition a whole into more parts, the larger the denominator;
- The numerator indicates the number of parts relative to the number of parts in the whole indicated by the denominator;
- Fractional amounts exist between whole numbers;
- Different denominators can be used to represent equivalent quantities;
- A multiplicative relationship exists between unit fractions (i.e.: one-sixth is one-half of one-third and one third is twice as big as one-sixth); and,
- The commutative and associative properties of addition (this big idea may emerge through student strategies)
- Quantities represented as a decimal are fractions limited to base ten denominators (i.e.: tenths, hundredths, thousandths, etc.)
- Quantities represented as a percent are fractions where the denominator is 100.
Measurement:
- Units of measure have different sizes and attributes; and,
- As the size of the unit of measure decreases, the number of iterations of that unit required to measure a quantity increases (and vice versa).
Math Talk
Ask students to reason through the following addition sentences.
It might be helpful to share a context that will serve to emerge the number line or bar model as a tool such as a caterpillar, worm or hare in a two-heat race or some other context of your choosing.
one and one sixth + one and one-third
one and one-half + one and five-eighths
three-eighths + one and one-fourth
one and two-ninths + one and one-third
It is possible that both the commutative and associative properties of addition can be highlighted through student strategies as they justify their thinking.
For example, in the third addition sentence, students might find it easier to model one and one-fourth first because it is a larger and friendlier number than three-eighths.
Spark Curiosity
Consider This Race…
Show students the following video of the Junior Divisional Championship Race:
In the video, students will notice that the view of the actual caterpillar “track” is blocked and therefore, they cannot see which caterpillar travelled the furthest.
Consider allowing students to predict which caterpillar crawled the furthest – keeping in mind that this prediction is truly a guess due to the limited information given.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Explain to students:
As you saw in the Junior Divisional Championship Race, it was impossible to determine the winner. However, the three different officials measuring had different preferences for representing the total distance in metres.
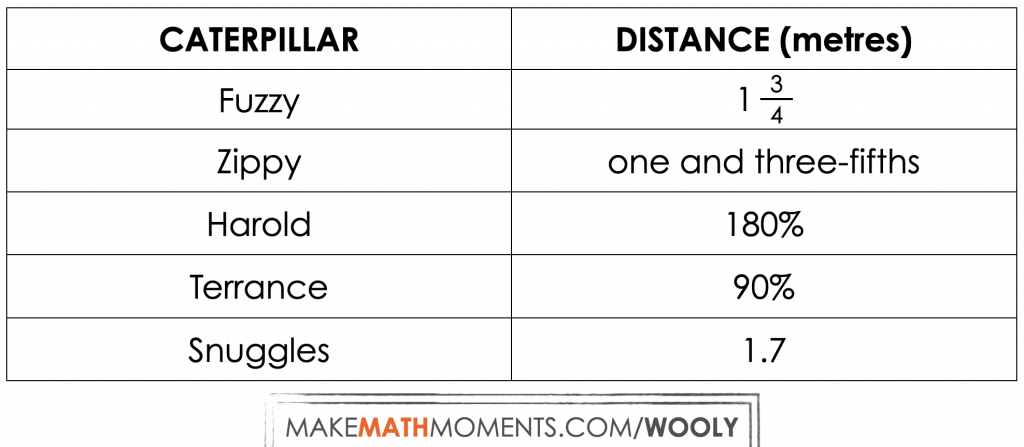
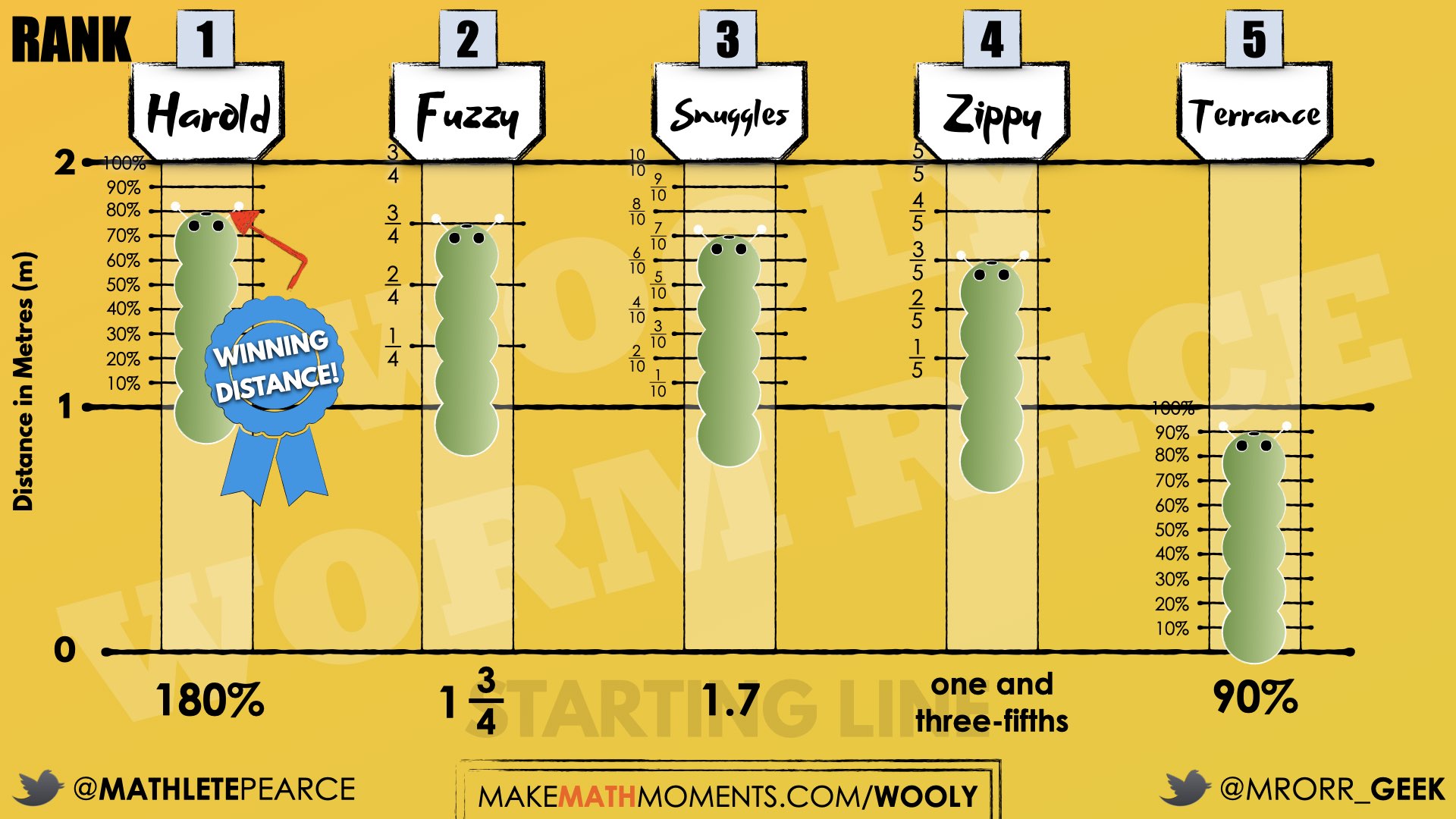
Here are the distances travelled by each of the caterpillars in the Junior Divisional Championship race:
Represent the distance travelled by each caterpillar and use your representations to order the distances from greatest to least.
As always, remind students that we will not be relying on the use of a calculator and that the most important work we will do here is creating a case to convince others of our thinking. There should be no yelling out of a final answer nor should you even share your final answer until you have described your reasoning to your peers.
It is critical that we continue to build a culture of thinking rather than a culture of answer getting to help each student along their journey to develop mathematical proficiency.
During Moves
While Students Are Productively Struggling…
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Student Approaches
Student Approach #1: Fraction Tiles
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Student Approach #2: Applying Known Facts
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Next Moves
Consolidation
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering this consolidation prompt to be completed independently.
Consolidation Prompt:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Resources & Downloads
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!