THE WOOLY WORM RACE [DAY 4]
FRACTIONS & METRIC UNITS
Represent, compare, order, and add fractions involving metric unit conversions.
Intentionality
Math Talk
Purposeful Practice
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview
Length of Unit: 6 Days
Access each lesson from this unit using the navigation links below
Students will continue developing their ability to represent fractions for the purpose of adding. We will also continue investigating the size, attribute of and relationship between metric units of measure.
Intentionality…
The purpose of the Day 4 activities is to reinforce key concepts from the previous lessons in this unit. Students will engage in a string of related problems through a math talk and will have an opportunity to complete independent purposeful practice. The math talk and purposeful practice serve to develop a deeper understanding of the following big ideas:
Number:
- Fractions can be represented in a variety of ways;
- How you partition the whole determines the fractional unit (i.e.: partitioning a whole into 6 parts will result in 6 sixth parts);
- As you partition a whole into more parts, the smaller the size of each part;
- As you partition a whole into more parts, the larger the denominator;
- The numerator indicates the number of parts relative to the number of parts in the whole indicated by the denominator;
- Fractional amounts exist between whole numbers;
- Different denominators can be used to represent equivalent quantities;
- A multiplicative relationship exists between unit fractions (i.e.: one-sixth is one-half of one-third and one third is twice as big as one-sixth); and,
- The commutative and associative properties of addition (this big idea may emerge through student strategies)
Measurement:
- Units of measure have different sizes and attributes; and,
- As the size of the unit of measure decreases, the number of iterations of that unit required to measure a quantity increases (and vice versa).
Math Talk
Ask students to reason through the following addition sentences.
It might be helpful to share a context that will serve to emerge the number line or bar model as a tool.
For example, leveraging the context of the Wooly Worm Race could be helpful using a story similar to:
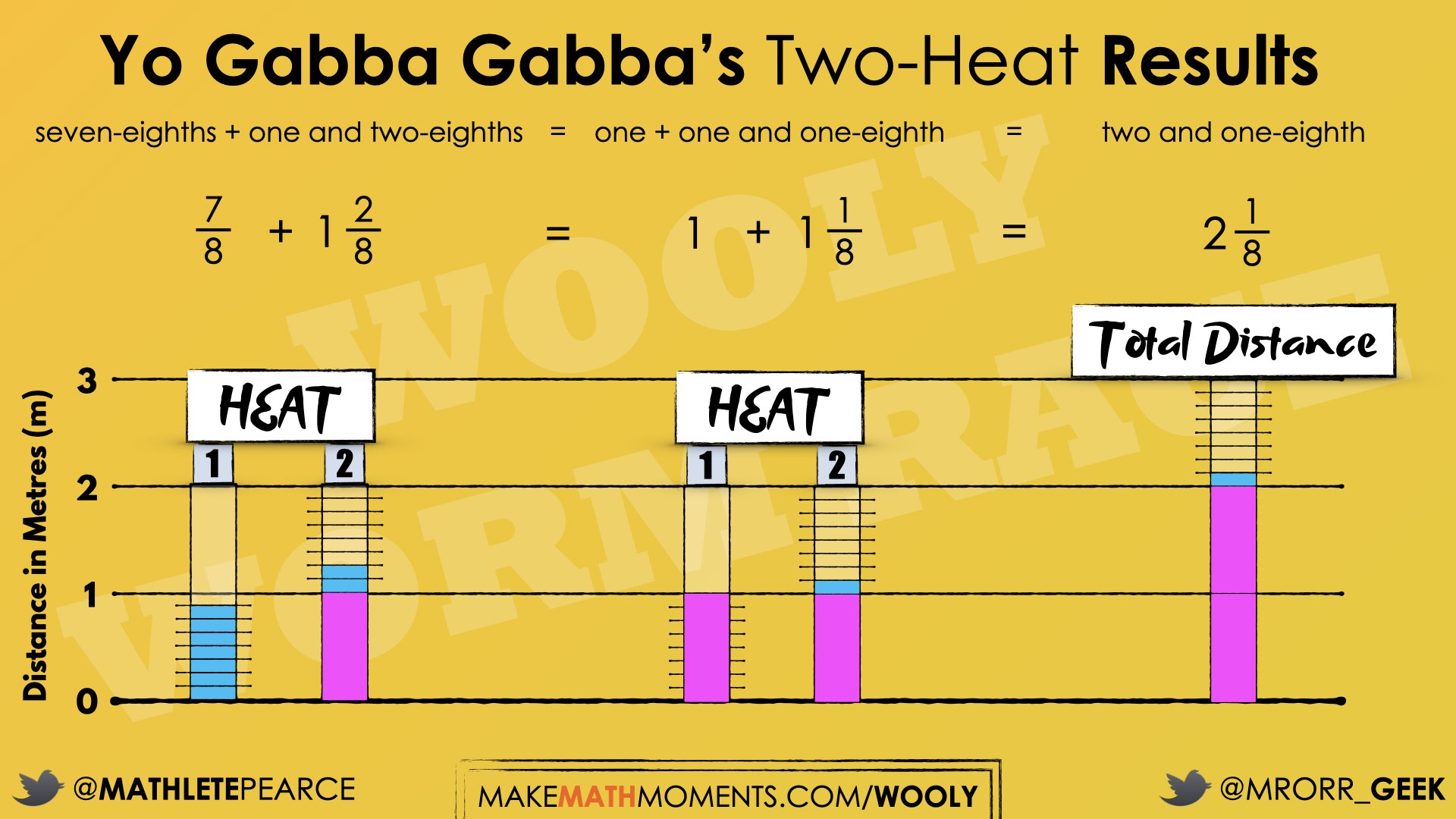
During off-season training, Yo Gabba Gabba practiced for a “two-heat” competition where the total distance of two races are measured to determine the winner. Here are the results measured for Yo Gabba Gabba. What was his total distance in each set of two-heats?
Big ideas that should emerge include the relationship between the denominators and equivalence.
three-fourths + five-fourths
seven-eighths + one and two-eighths
1 1/2 + 3/4
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
In this string we have used words as well as standard notation. We are also asking students to be flexible with both mixed numbers and improper fractions.
Through this string of related problems, it may be possible to highlight the commutative and associative properties of addition through student strategies as they justify their thinking.
For example, in the second expression, a student might see that ⅞ is one eight less than one. If they decompose the two-eights in the second addend, and add one-eight to the first addend, then they will be adding 1 and 1 and one-eight.
Watch this short silent solution animation to gain a better understanding of how the commutative and associative properties can be leveraged to handle this addition sentence more flexibly:
Here’s a screenshot of the final frame of the video:
Similar use of decomposing, disassociating, commuting and reassociating to compose a new, more helpful or convenient quantity can be leveraged in some of the other related problems in this string.
For example, in the last expression, a student may decompose and take 3/3 (or 1 whole) from the first addend and combine it with 6/6 (or 1 whole) from the second, leaving them with the opportunity to work with the remaining ⅓ and 5/6.
A student may further notice that adding ⅓ + ⅚ is the same as adding ⅓ + 4/6 + ⅙ or ⅓ + ⅔ + ⅙ which will result in 1 + ⅙ or 1 and ⅙ to be added to the other two wholes that were already created through leveraging the commutative and associative properties of addition.
Purposeful Practice
While Students Are Practicing…
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Questions: Representing and Adding Fractions & Selecting and Converting Metric Units
Question #1:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #2:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Question #3:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Resources & Downloads
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!