TILES AND TURTLES
GEOMETRY - TRANSFORMATIONS
Explore concepts relating to rigid motion transformations.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will examine traditional mosaic tilework to begin to develop an understanding of basic rigid motions and congruence.
Intentionality…
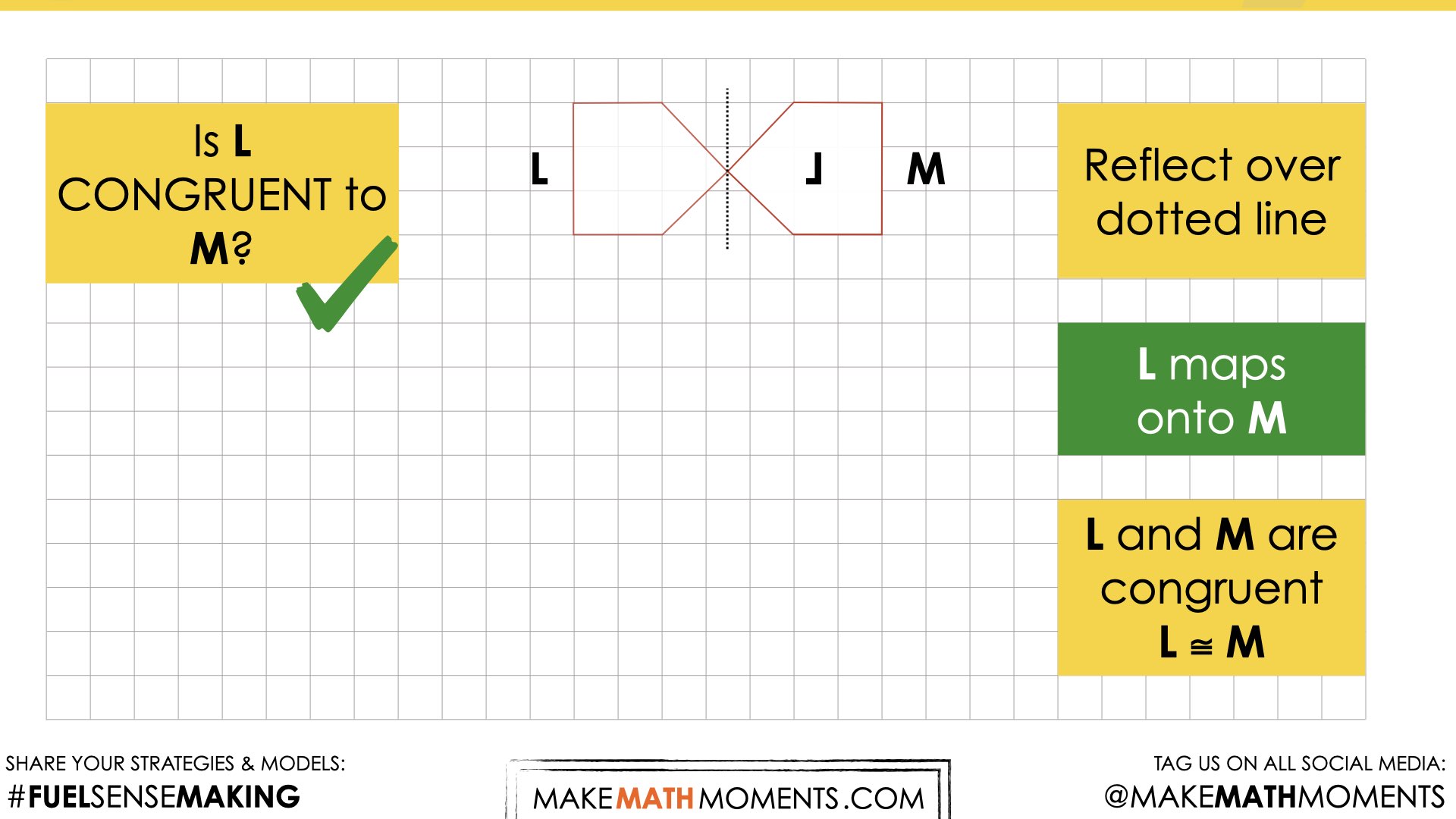
In this task, students will explore the definition of congruence, expanding on the “same shape and size” idea learned in previous years, to include the transformational approach to congruence. They will do so by examining traditional Moroccan mosaic tilework. This task serves to illustrate the idea that two figures are congruent if a series of basic rigid motions (translations, rotations, reflections) can be defined to map one figure onto another.
Some of the big ideas that will likely emerge in this task include:
- two figures on a plane are congruent if there exists a series of basic rigid motions that will map one figure onto another
- a property of rigid motion transformations (rotation, reflection, and translation) is that the measure of a two-dimensional object under the transformation remains unchanged
- basic rigid motions (translations, rotations, reflections) preserve distances and angle measures of figures
- when a figure is translated on a plane, segments connecting corresponding points will be parallel and congruent
- when a figure is rotated on a plane, segments connecting corresponding points via the point of rotation have the same angle measures
- when a figure is reflected across a line, segments connecting corresponding points are parallel to each other and perpendicular to the line of reflection
What You’ll Need…
A variety of tools for students to use to think through the problems, such as:
- Patty paper
- MIRA /GeoMirrors
- Grid paper
- scissors
- centimeter paper
- Whiteboards & markers
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students this video:
Then, ask students:
What do you notice?
What do you wonder?

Have students do a Think-Pair-Share routine:
- Students have individual think time to jot down ideas on paper or whiteboard.
- Students share their initial ideas with a partner.
- Students share as a whole group, either their own preference, or a meaningful observation they heard from their partner during the share (while giving credit to their partner). All contributions are acknowledged and recorded on an anchor chart on the board.
Spending time to acknowledge and address specific thoughts that students shared, whether a notice or a wonder, is crucial to building a culture in your classroom where students know that their voice is being valued and thus encourages them to continue sharing their thoughts and opinions later in this lesson and in future lessons.
Possible observations and questions that may come up include:
- I notice that all the photos are of tile work
- I notice that the tiles have radial patterns
- I notice that the patterns have symmetry
- I wonder how they make the tiles
- I wonder who makes them and how long it takes
- I wonder what they’re made of
- I wonder if the tiles are painted first, then assembled, or assembled then painted
- I wonder how they make the design of the tiles
Notice and Wonder 2
The second part of the Notice and Wonder routine focuses on answering some of the questions related to how the tile work is made, and hopefully spark some new questions. The video shows some of the tools and techniques a craftsman uses to create a small tile.
Show students the following video:
Then, ask students:
What more do you notice? What else do you wonder?
Share your thoughts.

Possible observations and questions that may come up include:
- I notice that he chips the tile twice (once in the front, once in the back)
- I notice the tiles are painted before he starts to cut them
- I wonder how the tiles all fit together
- I wonder if all the same tiles are exactly the same (or else the pattern doesn’t work/fit)
- I wonder how he gets all the tiles to be the same without a machine
Estimation: Prompt
Once students’ initial ideas have been acknowledged and noted, the class can settle on a question to explore:
Are all the same colour pieces congruent?
Make an estimate.
Facilitator’s note: Students have likely been introduced to the word “congruent” in earlier grades. Congruence is often introduced as meaning “same shape and size” which is an intuitive definition. In high school, congruence is often approached from a triangle congruence criteria perspective. Understanding congruence through transformations is a critical bridge between the two.
It may be worthwhile to consider beginning an anchor chart that records students’ ideas about congruence as they shift from the measurement definition (same shape and size) to the transformational definition (two polygons are congruent if it is possible to describe a series of transformations that maps one polygon onto the other). A simple prompt/title for the anchor chart might be: “Two shapes are congruent if…”

Students begin by creating a hypothesis before they are provided with all the information they need to answer the question, thus providing students who may be reluctant to share with a safe entry point.
Be sure not to skip over asking students to make an estimate using only their spatial reasoning skills as this is a very important step in the Curiosity Path. Providing students an opportunity to make an estimate and try to articulate their thinking with their peers provides a very low floor opportunity for them to not only better understand the context, but to also begin nudging them to think about what will be important to make their estimate more precise as we continue through the lesson.
Students should be given an opportunity to share their ideas at this point, but refrain from sharing their rationale just yet in order to give everyone a chance to develop their own thinking.
Have students turn to a partner and generate questions they could ask that would provide them with information they could use to answer the question. Ask students how they would use the information to answer the question.
Prompt:
What information might be helpful to answer this question?
How might you use that information?
Estimation: Partial Reveal
Reveal to students the video showing how the tiles are made and assembled. Students may wish to update their predictions about which sets of tiles are congruent.
At this point, students will likely have an intuitive sense, or definition for congruence as being “same shape and size”. They may also suggest that corresponding angles and sides are congruent. Nonetheless, it is valuable for students to spend time exploring these ideas before further deepening their understanding to include transformation as an essential characterization of congruence.
Provide students with a copy of the tile pattern and prompt them to construct viable arguments in order to prove that pieces of similar color are congruent (or not).
Facilitator’s note:
It is worthwhile to consider giving students prompts that do not have a coordinate grid. It can help students who are just beginning to work with transformations get a sense of the general meanings for each type of transformation. Additionally, it is valuable in making explicit some of the relationships between figures. For example, connecting corresponding points on an image and a pre-image will highlight relationships that students may not consider on a coordinate grid. The same tile pattern is considered using a coordinate grid as part of the activities on Day 3 of this unit.
Some strategies that students may use include:
- cutting out different pieces and placing them on top of one another
- tracing different pieces on patty paper and placing them on top of one another
- measuring side lengths and comparing corresponding lengths on another figure
- measuring angles and comparing corresponding angles on another figure
Facilitator’s note: As students construct their arguments for or against the congruence of figures, this may be an opportunity to bring in some of the vocabulary associated with congruency, including:
- “distance preserving” (a transformation is distance preserving’ if the measures of corresponding distances on congruent figures are the same)
- “angle preserving” (a transformation is ‘angle preserving’ if the measures of corresponding angles on congruent figures are the same)
Fuel Sense-making
Crafting A Productive Struggle: Prompt
To begin the sense making portion or the lesson, begin by providing students with a definition of “congruence” striving for a shared understanding, then encourage students to use this definition to construct a viable argument for or against the congruence of same coloured figures in the tile:
Two figures are CONGRUENT if we can describe a series of rigid transformations that would map one figure onto the other.
- translations (slides)
- rotations (turns)
- reflections (flips)
Construct a viable argument that shows which sets of tiles are congruent.
Optional: you may consider showing students the following short video that shows how the tiles are designed.

Provide students with an additional copy of the tile design (with or without grid lines) if needed. Note: Grab a copy of this in the Resources & Downloads area.
Do consider making the following tools available to students without explicitly directing students to use them:
- Scissors
- Patty paper
- Acetate sheets
- Centimeter paper/grid paper
- Rulers
- Protractors
- GeoMirrors/MIRA
Remind students to refrain from shouting out answers, and be sure to emphasize the importance of creating a viable argument.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse.
Listen and observe as students revise their hypotheses. Are students able to accurately and precisely describe transformations?
- Translations require a distance and a direction
- Rotations require a center of rotation, degree of rotation and, at this stage, direction (clockwise or counterclockwise)
- Reflections require a line of reflection.
How are students approaching the problem? What strategies and mathematical models are they leveraging? Are they:
- Cutting out figures and moving them across?
- Using measurement techniques to measure distance or angles?
- Accurately identifying corresponding vertices on congruent figures?
- Able to logically sequence more than one transformation?
- Using precise language to describe the transformations?
This is an opportunity to make note of where students are developmentally. Prompt students to explain their thinking and how they plan to use their model/strategy to determine the translations for each set of figures.
Students will also likely discover that the blue squares in the corners of the tile are not congruent to the other blue squares. Consider challenging students who may be ready for an extension to begin to consider dilations by asking them how much bigger the corner squares are, and the connections between the relative dimensions of the squares and their relative areas. However, dilations are not a focal point of this lesson.
Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
Common misconceptions you may consider noting include:
- Misidentifying corresponding vertices on images
- Confusing rotation and reflection
- Not understanding how the relative location of sides and vertices change
During the consolidation phase, prior to asking students to share their own strategies and reasoning, ask the class if they can discern how the students whose work is being shared were thinking about the problem. A possible prompt might be:
Can you tell how this student/group was thinking about the problem?
This encourages all students to consider alternative viewpoints and begin to seek connections between representations. It helps set up the mindset of “listening to understand” when students share their work. It also highlights the importance of communicating mathematical ideas clearly.
Have students share their strategies and reasoning for how different figures map onto each other to show congruence. Ask them to convince you and their peers that their answer is correct.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
Student Approach #1: Cutting out and moving figures

Option A
I cut out the shapes and put them on top of the other shapes to see if they were the same shape and size.
Student Approach #2: Trace and compare

Option B
I traced the shapes onto tracing paper, then I overlaid it onto the other shapes to see if they matched. All the same color shapes matched except for the blue squares in the corner, which were bigger.
Student Approach #3: Measure and compare
Option C
I measured the sides of the shapes with a ruler. I realized that most of the blue squares were all the same size, except for the four in the corners, those were bigger so not congruent.
Next Moves
Reveal 1
Show students the following reveal video:
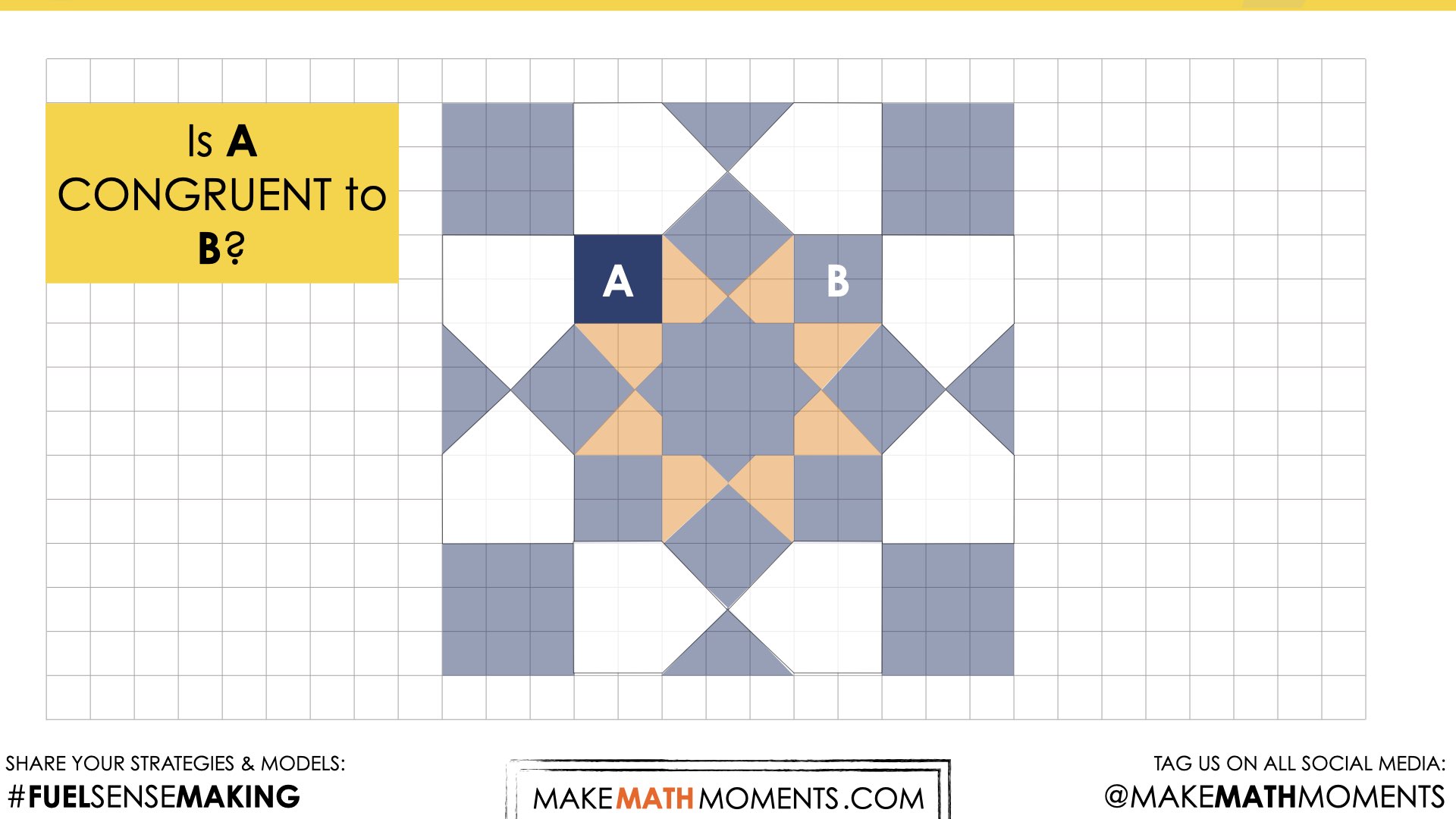
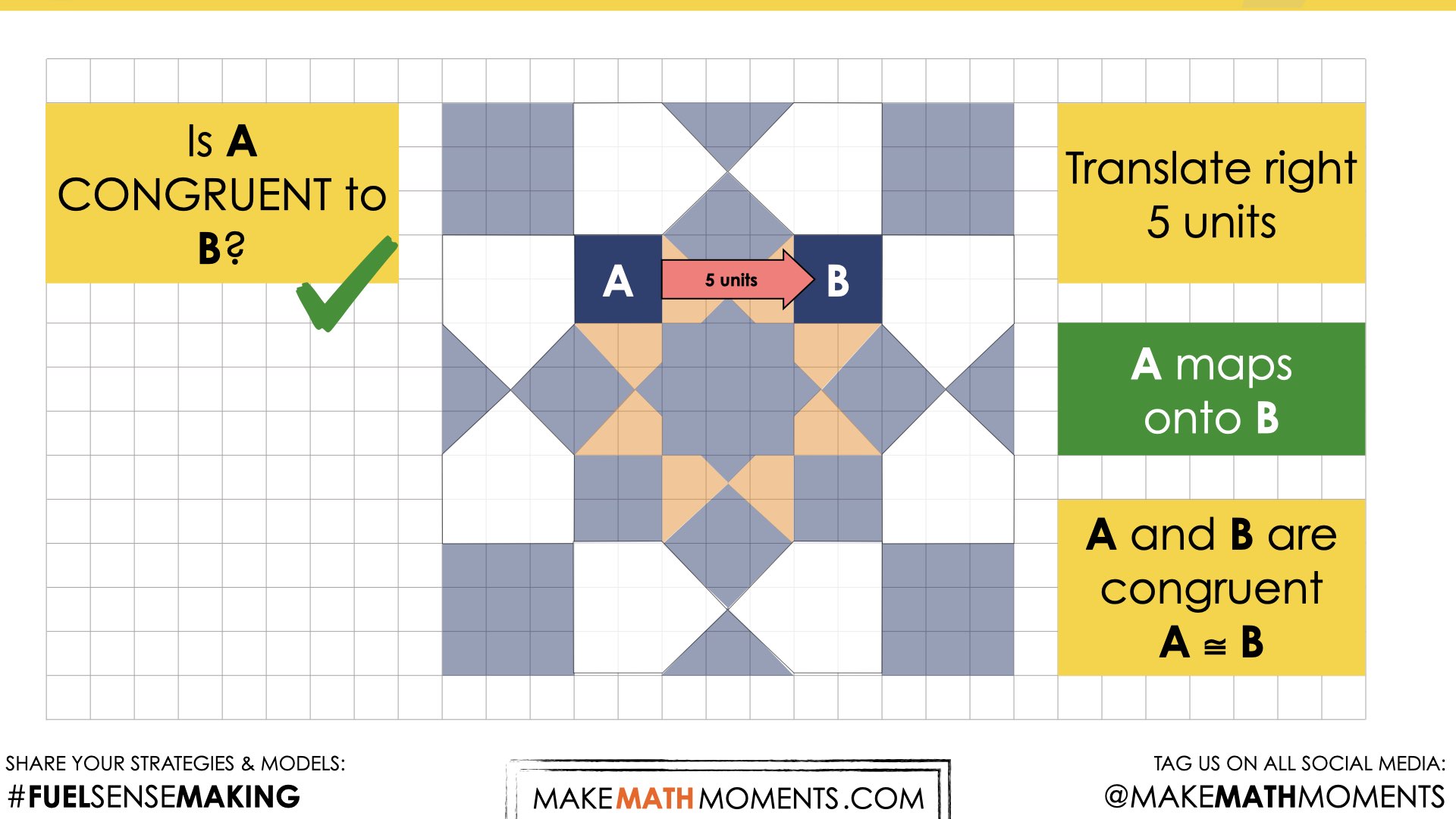
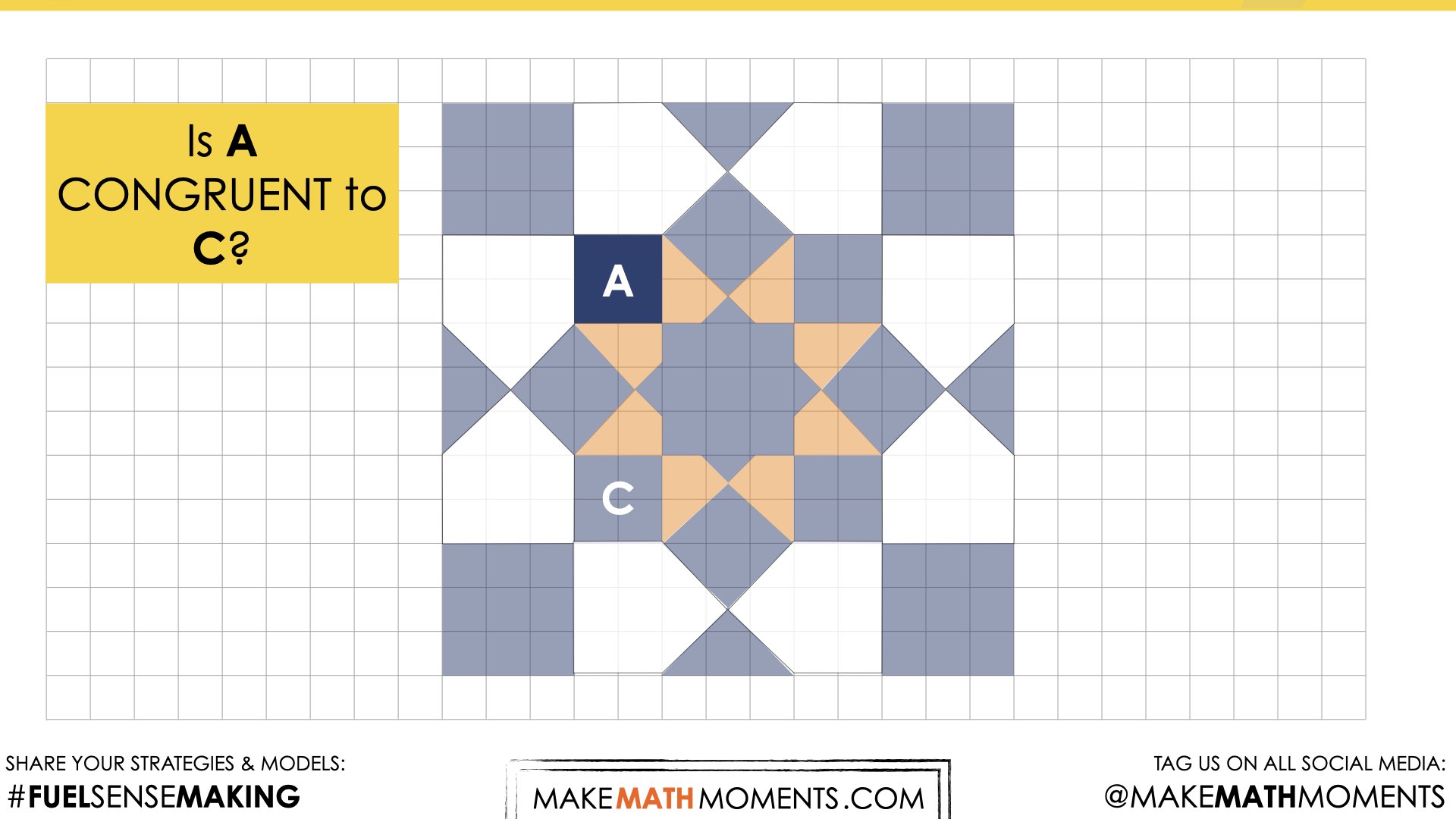
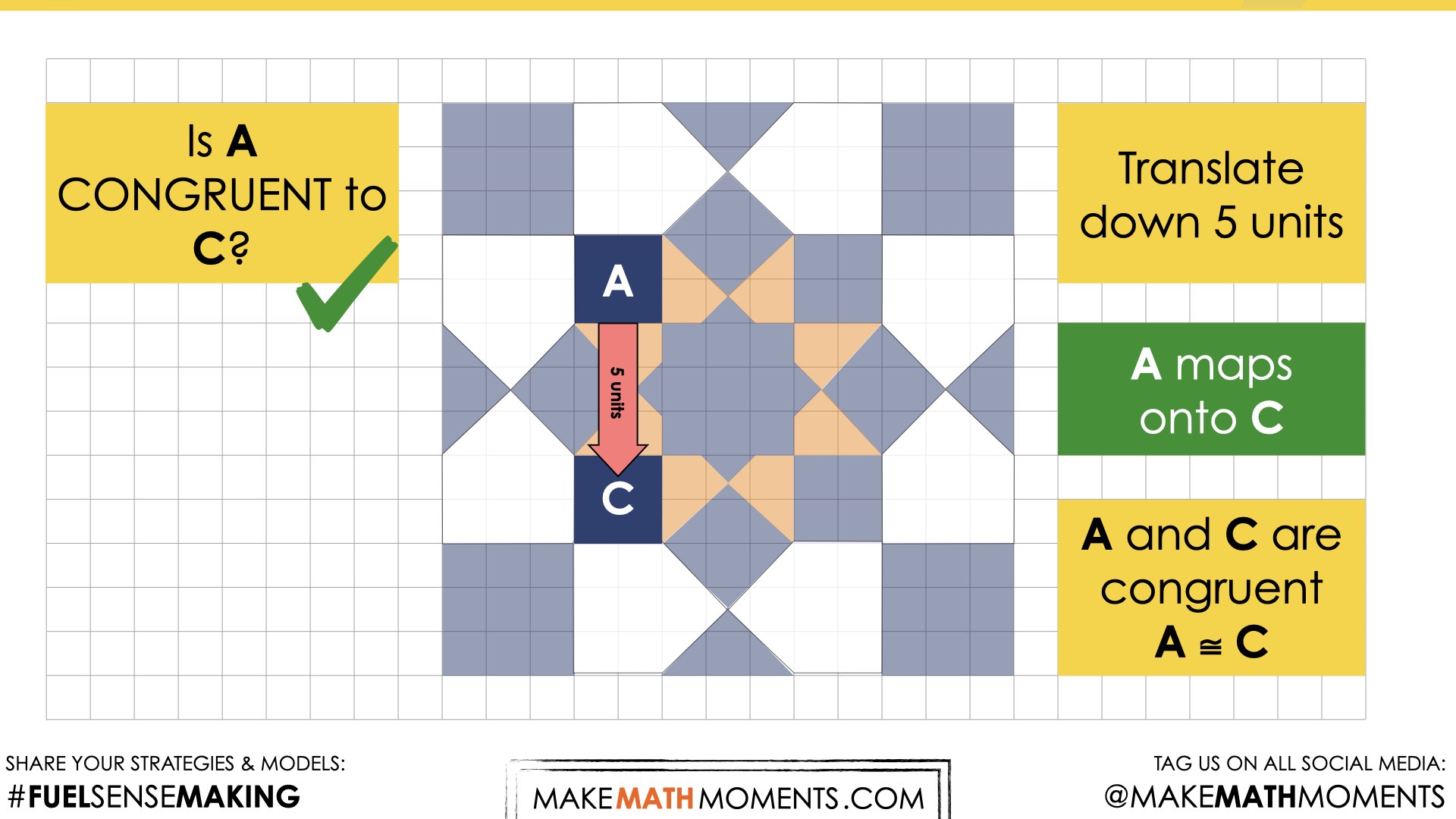
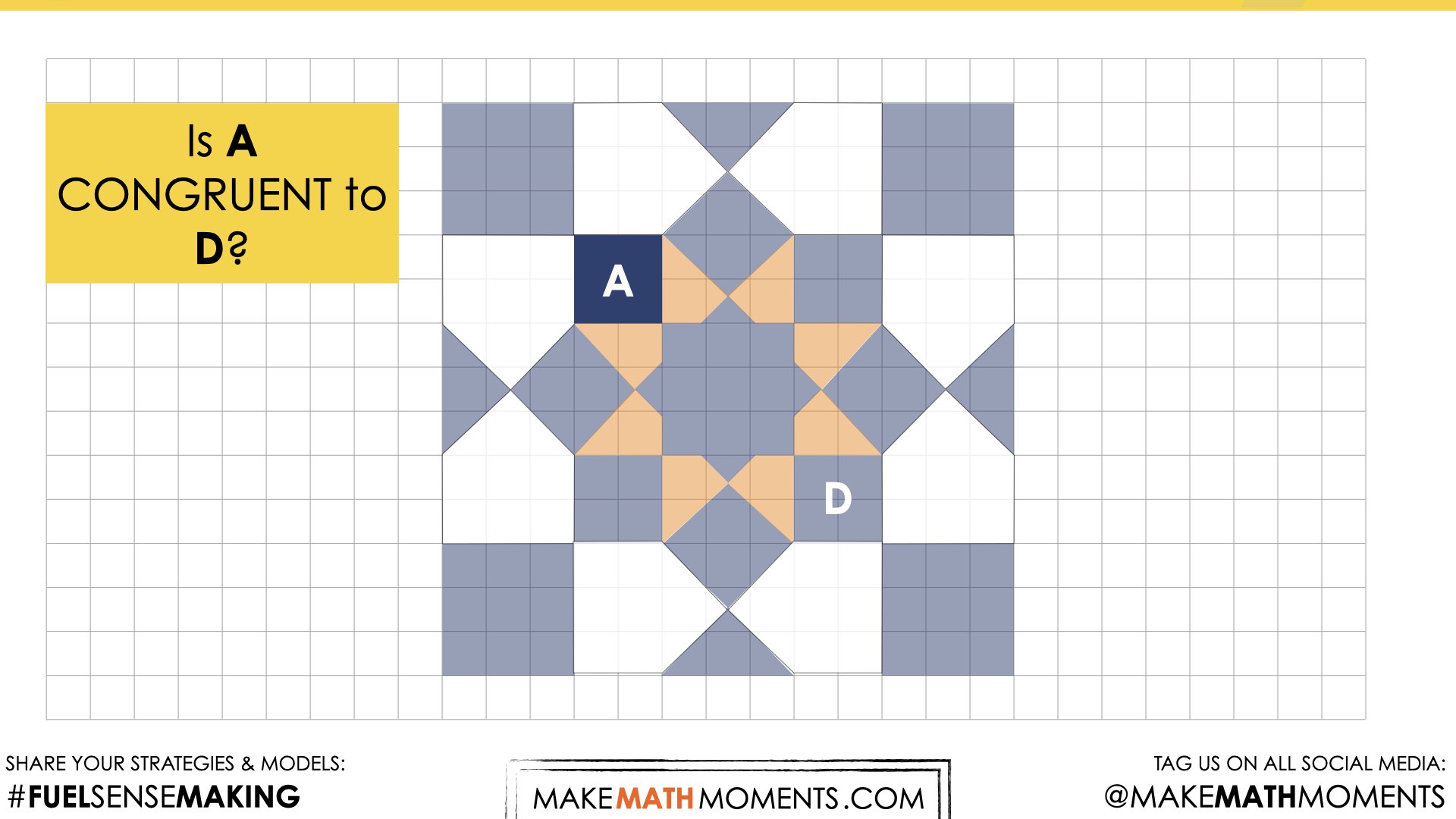
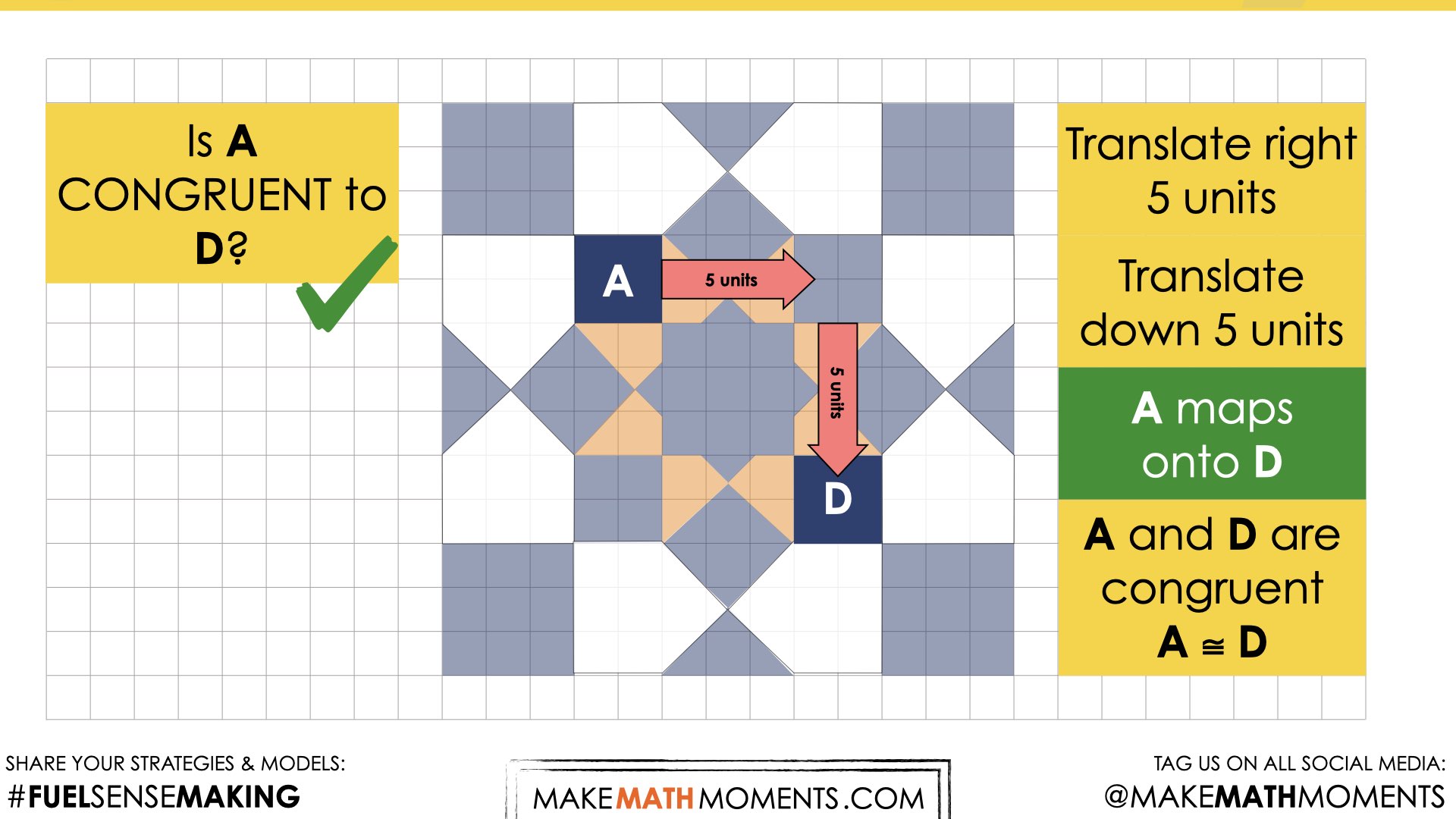
Reveal 2
Show students the following reveal video:
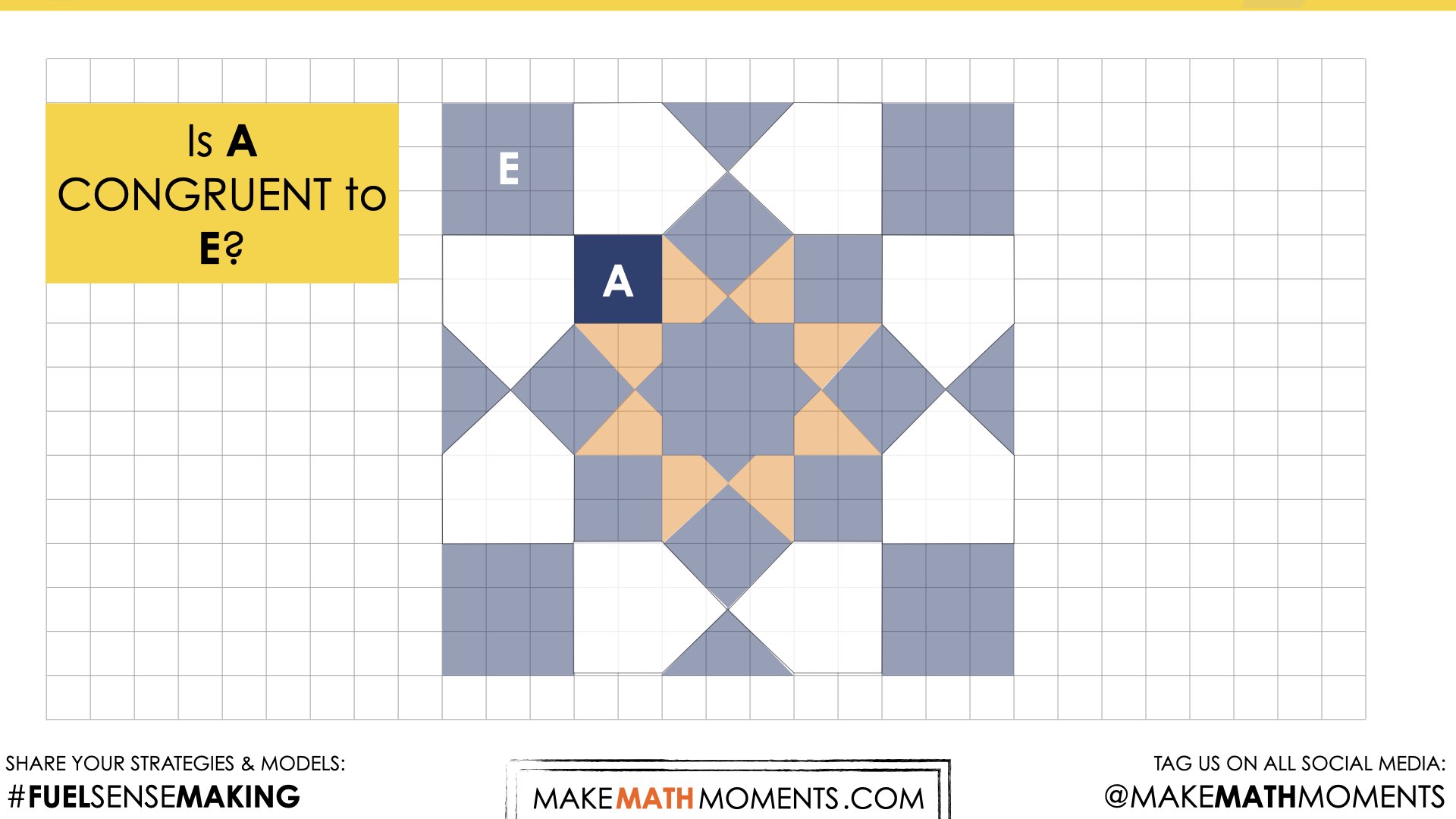
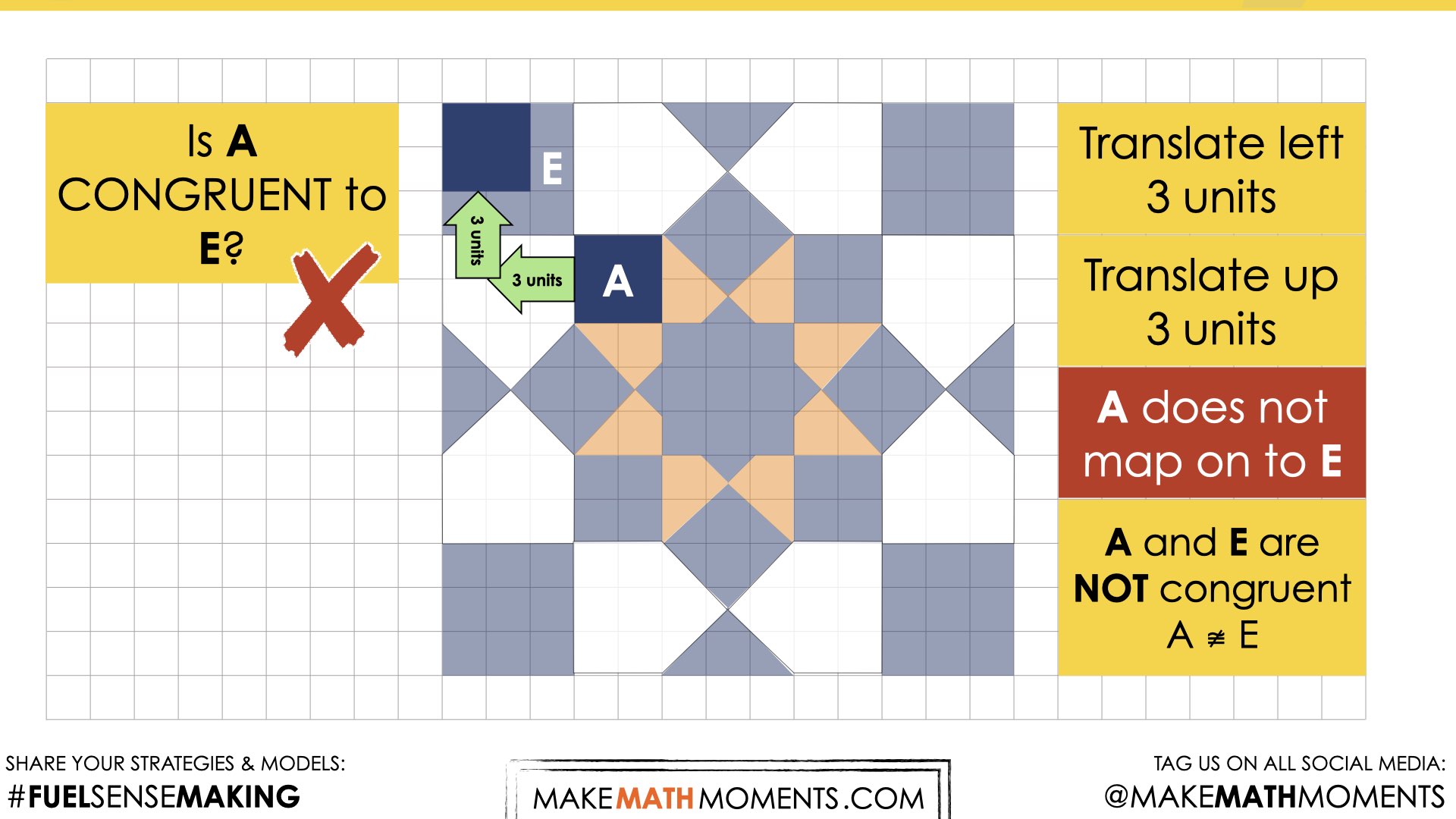
Reveal 3
Show students the following reveal video:
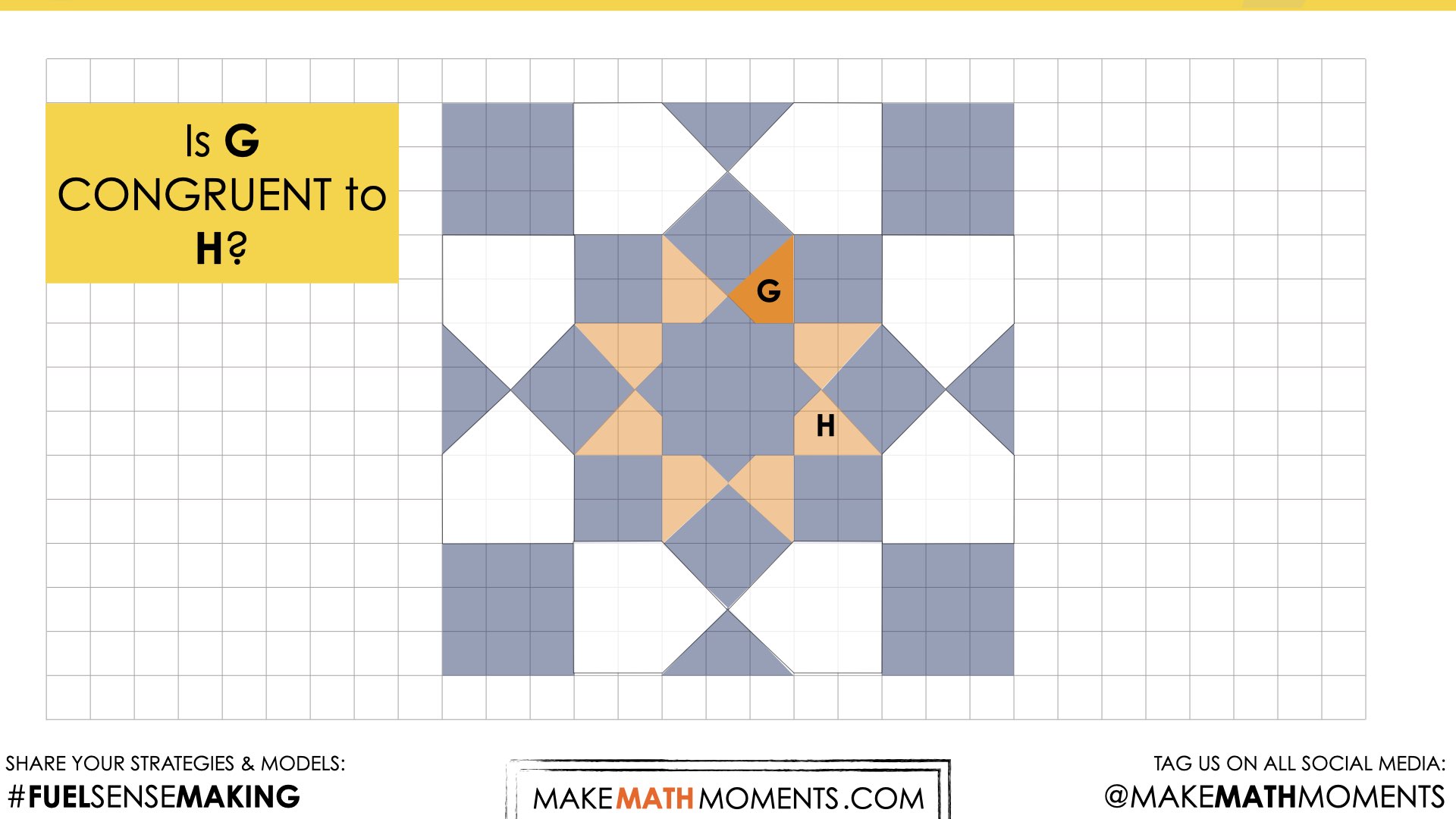
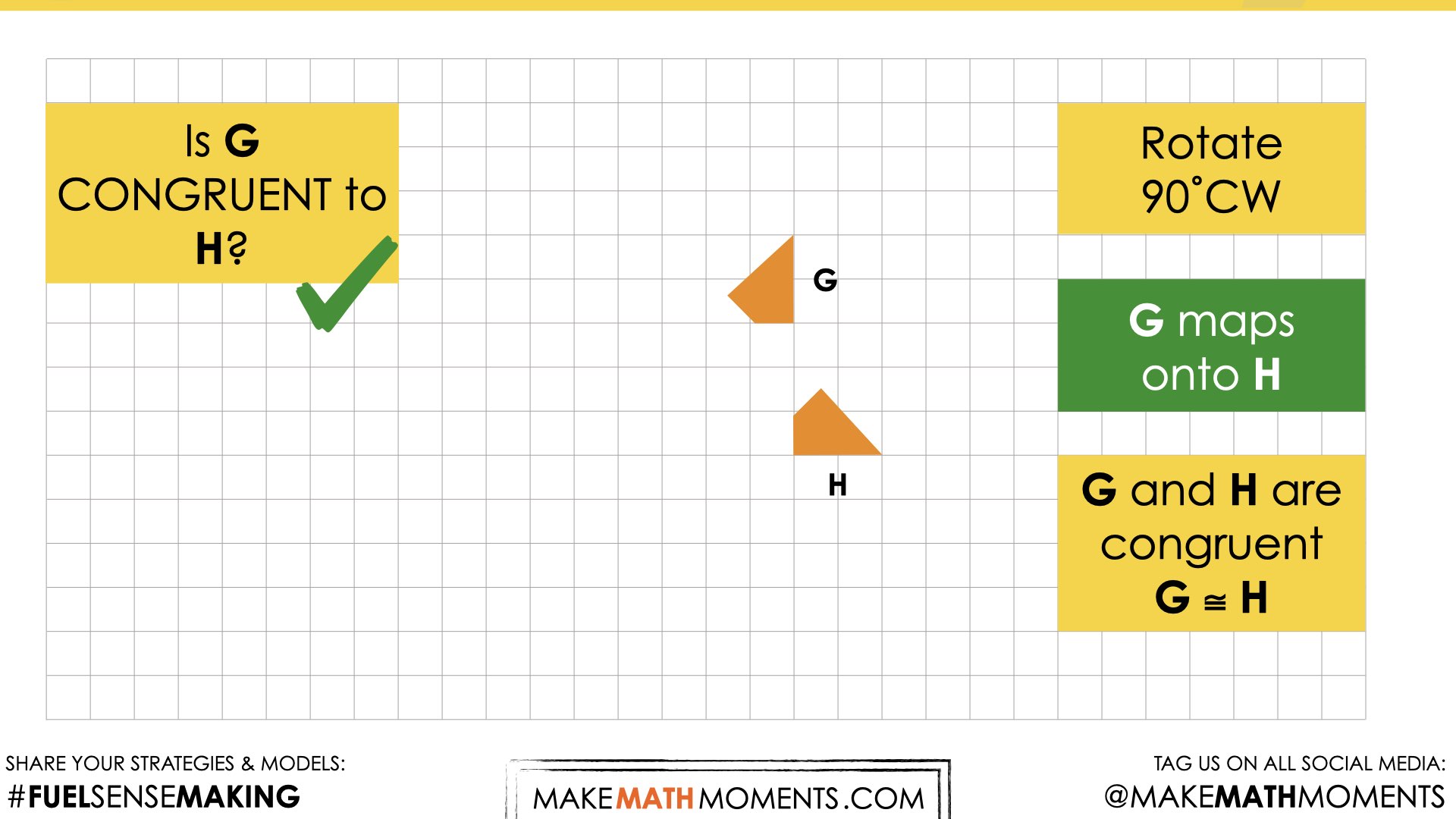
Reveal 4
Show students the following reveal video:
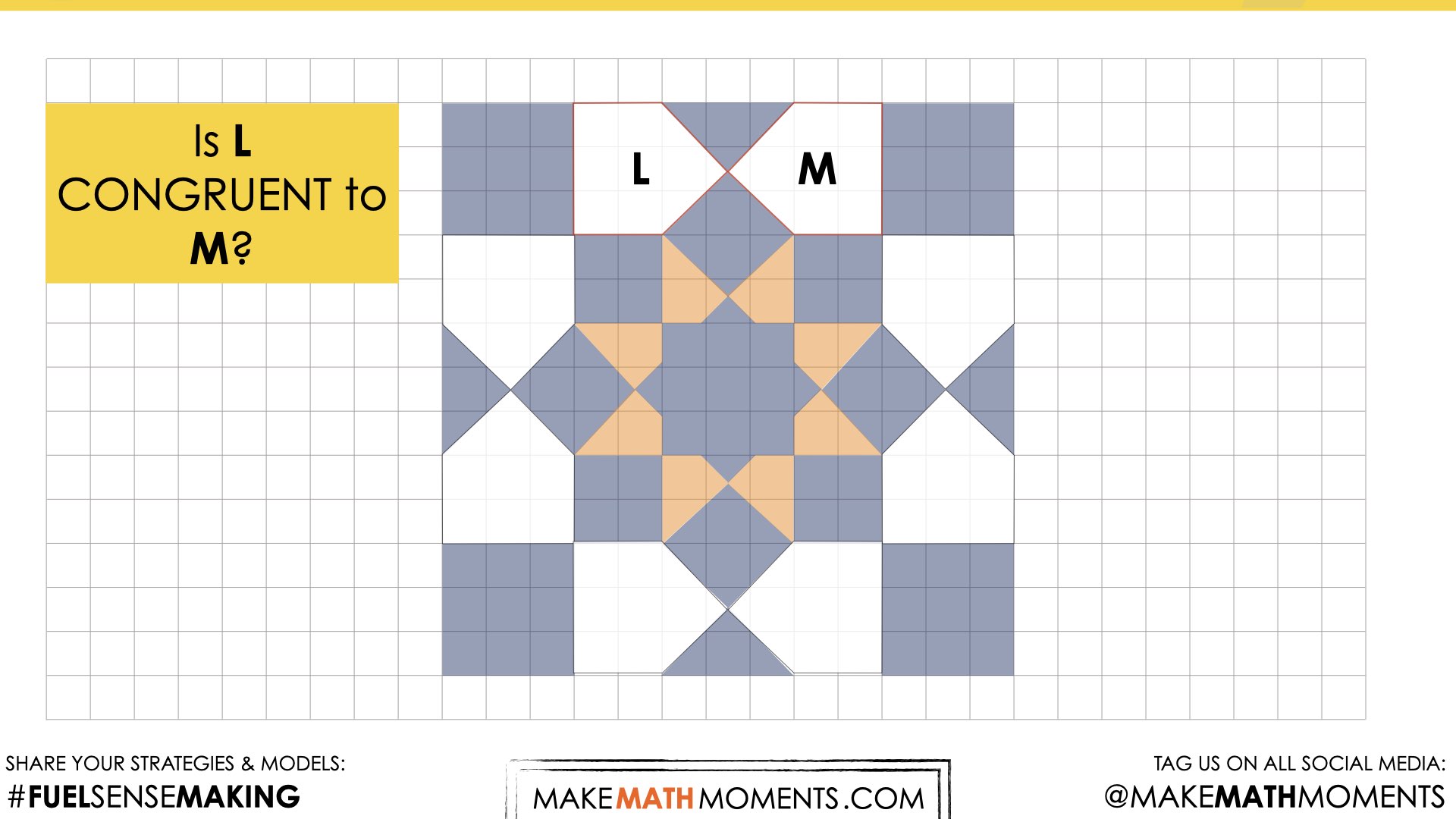
Consolidation
During consolidation, highlight how students went about comparing the options.
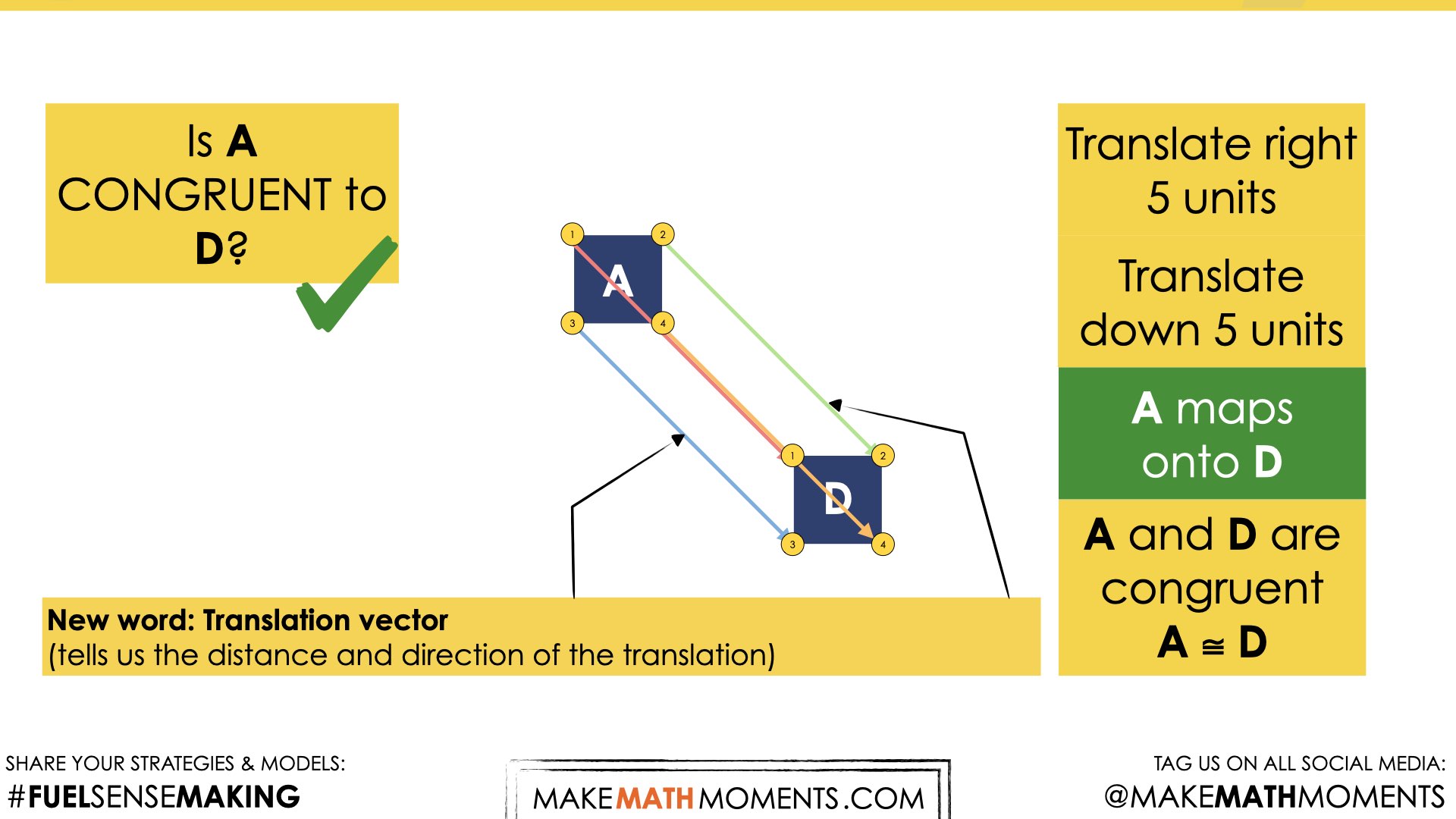
As you are discussing student solutions, there is the opportunity to highlight the connection between segments that connect corresponding points on images and preimages. The corresponding reveal slides have the segments already drawn, however this could also be done using the images drawn by the students as they share.
Beginning with translations, once it has been established that a figure can be mapped onto another, discuss how the segments connecting corresponding points are related.
Prompt:
What do you notice? What do you wonder?
Conduct a Think-Pair-Share where students first have a moment to consider the question on their own, then turn and talk to a partner, then share as a whole group. Students will likely notice that the translation vectors are both parallel and congruent.
Challenge students to consider whether or not this would be true for any translation and how they might go about convincing their mathematical community.
Continuing with with rotations, once it has been established that a figure can be mapped onto another, discuss how the segments connecting corresponding points via the rotation point are related.
Prompt:
What do you notice? What do you wonder?
Conduct another Think-Pair-Share where students first have a moment to consider the question on their own, then turn and talk to a partner, then share as a whole group. Students will likely notice that the segments form congruent angles.
Again, challenge students to consider whether or not this would be true for any translation and how they might go about convincing their mathematical community.
Lastly, explore reflections, discussing how the segments connecting corresponding points are related.
Prompt:
What do you notice? What do you wonder?
Students may notice that corresponding points are equidistant from the reflection line, that the segments connecting corresponding points are parallel, and that they are perpendicular to the line of reflection. If all of these points are not mentioned by students, consider bringing it to their attention, although more emphasis will be placed on reflections on Days 2-3 of this unit.
Reflect and Consolidation Prompts
Consider asking students to complete the following consolidation prompt independently.
This prompt is deliberately formulated as a task to be performed off the coordinate plane. The purpose is to uncover an essential aspect of translations – that lines drawn from anchor points in a pre-image to corresponding points on the resulting image are parallel and congruent to other lines from other anchor points.
Students may notice that the lines between the anchor points on the preimage and the corresponding points on the resulting image are congruent. Consider encouraging students to verify this using some form of measurement.
Although the prompt echoes the discussion from the consolidation phase of this task, this is still an opportunity to identify any individual misunderstandings or misconceptions.
Consolidation Prompt #1:
The turtle needs some shade to cool down!
Move (translate) the turtle by placing it on the rock under the tree.
Describe the translation.
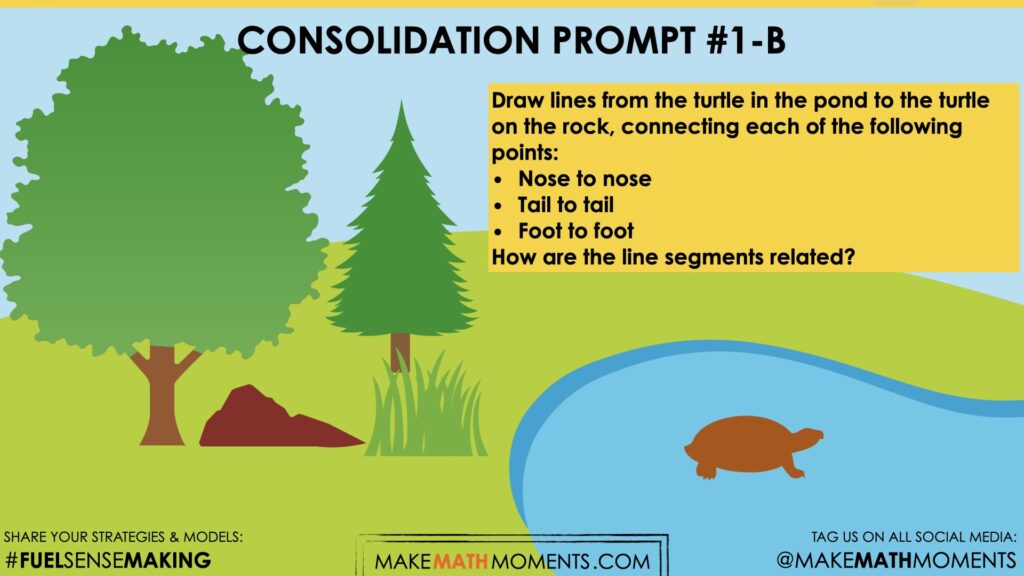
Draw lines from the turtle in the pond to the turtle on the rock, connecting each of the following points:
- Nose to nose
- Tail to tail
- Foot to foot
How are the lines related to each other?

Consolidation Prompt #2:
Move the turtle so that it can have a face-to-face conversation with the frog. Describe the transformation.
Draw a line from the turtle in the pond to the frog, and then to the turtle who is face to face with the frog, connecting each of the following points:
- Turtle nose to frog to new turtle nose
- Turtle tail to frog to new turtle tail
- Turtle foot to frog to new turtle foot
How are the line segments related to each other?


Consolidation Prompt #3:
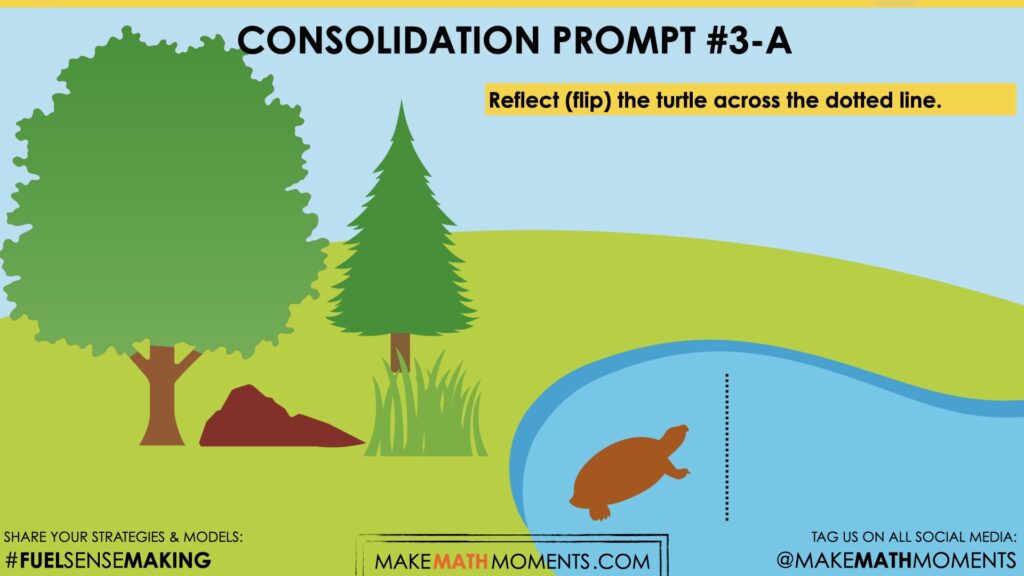
Reflect (flip) the turtle across the dotted line.
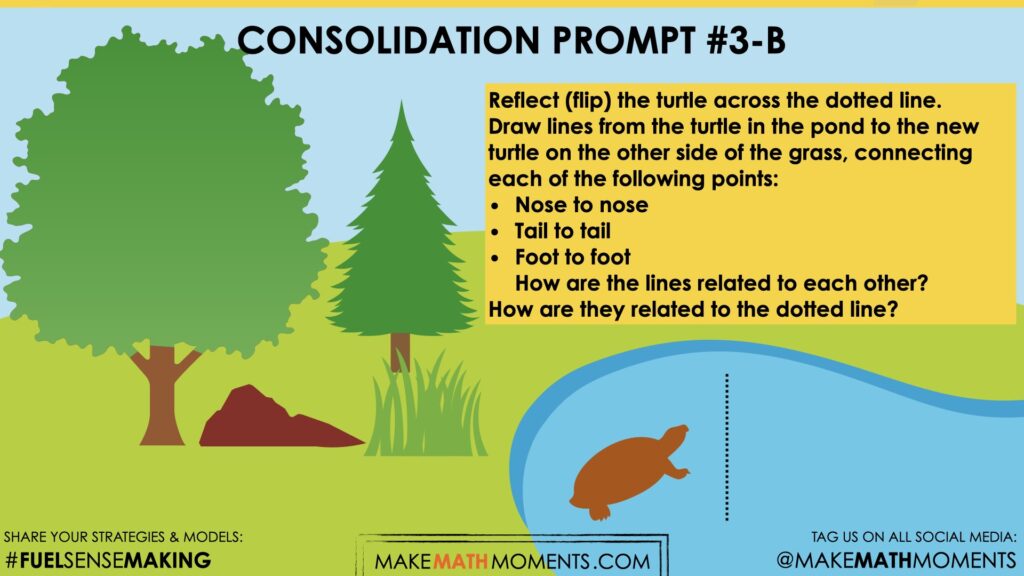
Draw lines from the turtle in the pond to the new turtle on the other side of the grass, connecting each of the following points:
- Nose to nose
- Tail to tail
- Foot to foot
- How are the lines related to each other?
How are they related to the dotted line?
Consolidation Prompt #4:
Is A CONGRUENT to F?
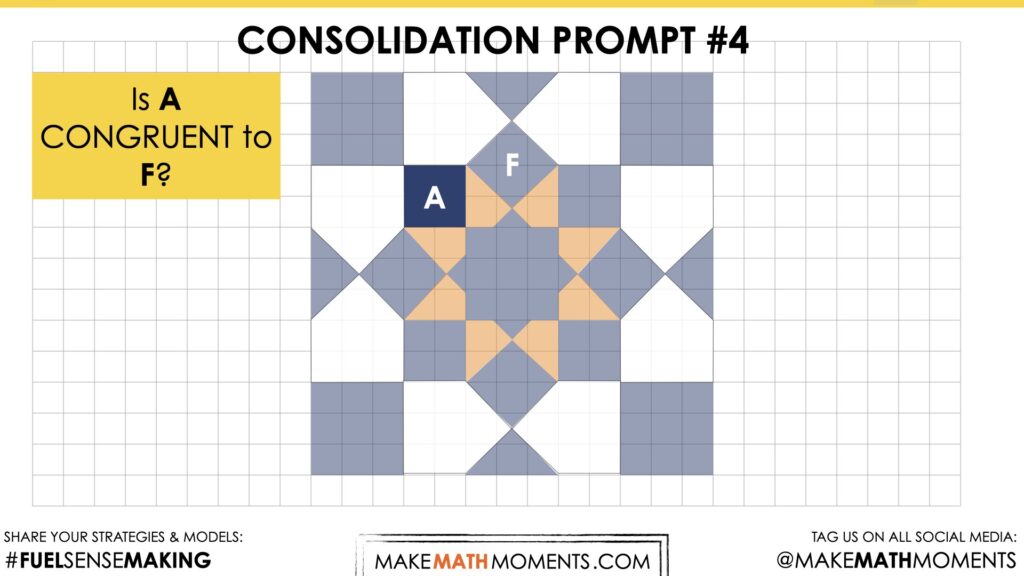
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!




