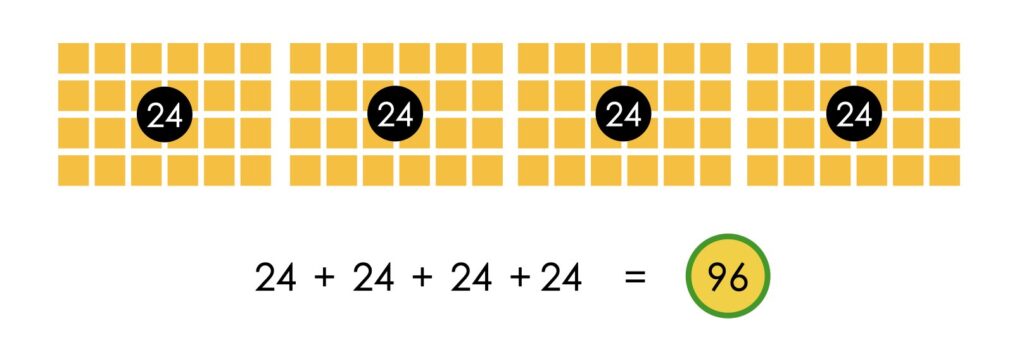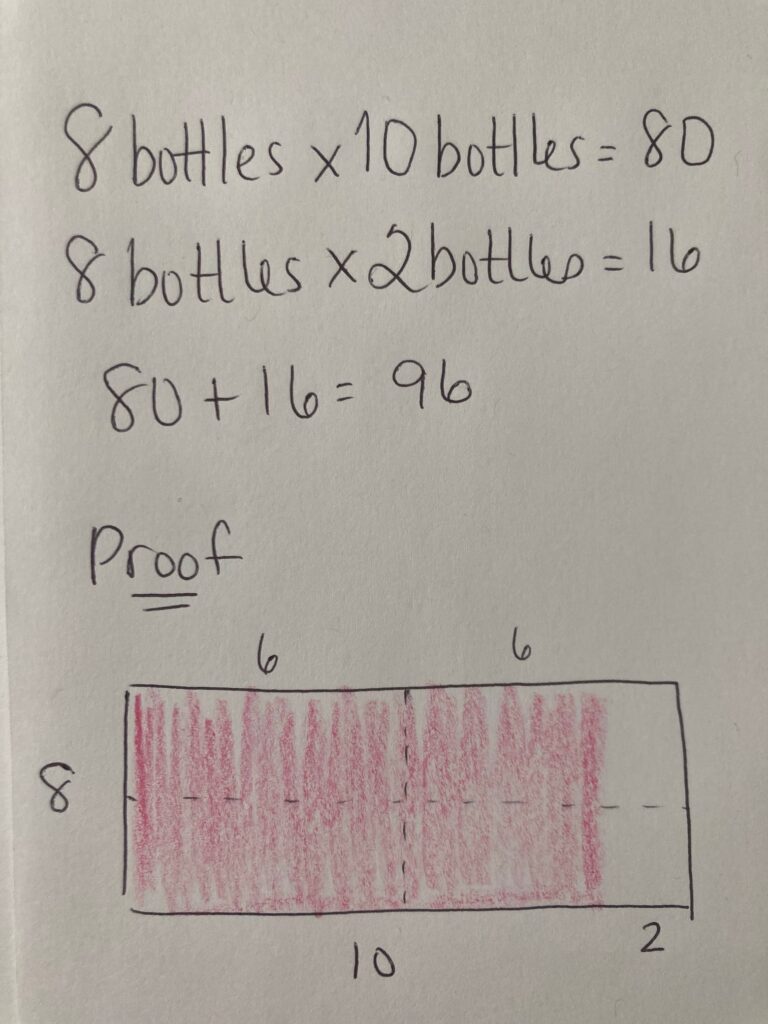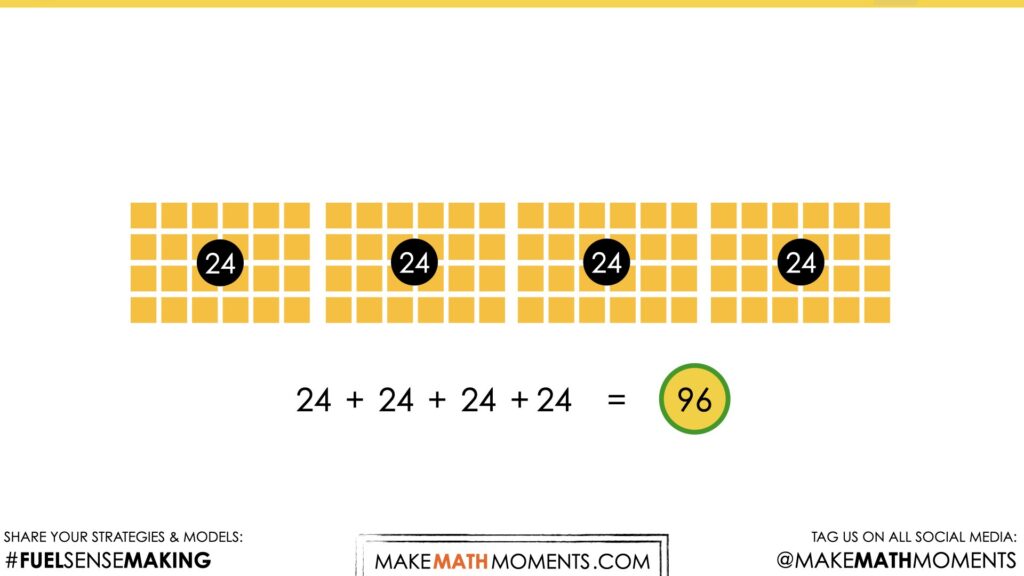STACK 'EM UP
MULTIPLICATION: 1- & 2-DIGIT WHOLE NUMBERS
Introduction to 1- and 2-digit multiplication through context in order to emerge associative, commutative and distributive properties and models including the array and area model.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview
Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will determine the number of bottles of juice stocked on a grocery store shelf.
Intentionality…
In this task, students will determine the total number of bottles of orange juice on the shelf. The organization of the cases in rows and columns will serve to emerge the array model as a tool for thinking. The associative, distributive and commutative properties of multiplication can be explored through this context and model. Some of the big ideas that may emerge through this task include:
- Multiplication can involve determining the total quantity given the number of equal groups and the size of each group;
- The order of the numbers in a multiplication sentence does not matter due to the commutative property;
- The strategy of doubling and halving is possible due to the associative property of multiplication;
- The distributive property of multiplication supports the strategy of partial products (where one or both factors can be decomposed over addition or over subtraction).
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Replaying the video can be helpful here.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group. Be sure to write down these noticings and wonderings on the blackboard/whiteboard, chart paper, or some other means to ensure students know that their voice is acknowledged and appreciated.
Some of the noticing and wondering that may come up includes:
- I notice a case of juice.
- I notice it is orange juice.
- I notice there are 24 bottles of juice.
- I notice it is a 4 by 6 array.
- I wonder how much the case costs.
- I wonder if this juice is from a store.
- I wonder how many cases there are.
- I wonder how big the bottles are.
- I wonder who the juice is for.
At this point, you can answer any wonders that you can cross off the list right away. For example:
- This case of orange juice is sold at the local grocery store.
- There are 24 bottles in a case.
- Each bottle has 10 oz of juice.
- The cost is $21.95 before tax.
Estimation: Prompt
After we have heard students and demonstrated that we value their voice, we can land on the first question we will challenge them with:
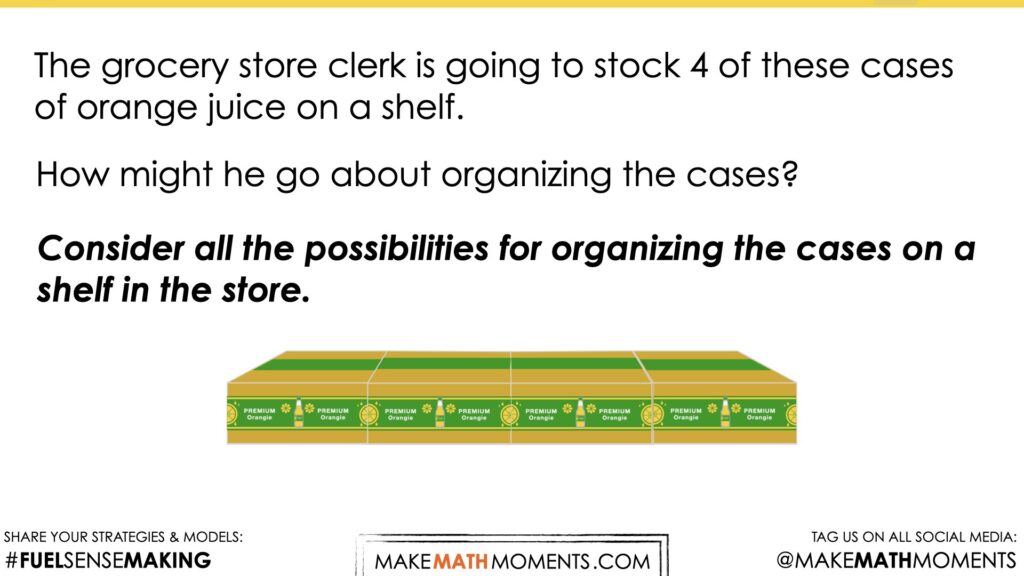
The grocery store clerk is going to stock 4 of these cases of orange juice on a shelf. How might he go about organizing the cases?
Consider all the possibilities for organizing the cases on a shelf in the store.
We can now ask students to predict how the grocery store clerk will organize the four cases. As you are observing the students draw various diagrams, ask them whether or not they can describe their diagram with one or more multiplication sentences.
Update Estimate: Update & Reveal
Ask a few students to share their diagrams. How they believe the cases will be stocked on the shelf.
Show the following video of possible solutions:
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Student prompt:
Determine the total number of bottles of orange juice in 4 cases of orange juice. Justify your thinking.
Be sure to remind students that they are not to use a calculator to determine the number of bottles as using that tool will rob them of this mathematical experience. Students should use a mathematical model in order to communicate their thinking.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Concrete manipulatives to create four 4 x 6 arrays
- Visual array of four 4 x 6 arrays
- An open-array using partial products
- A flexible algorithm using partial products
Have students share their strategies and reasoning for how to represent the number of bottles in both 4 cases. Ask them to convince you and their peers that their answer is correct by sharing mathematical models.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
Student Approach #1: Pictorial Array (Digital) and Repeated Addition
I showed the four cases from above stacked in a line, using a color tile tool to make the four cases. I counted that each case has 24 bottles. So then I added 24 + 24 + 24 + 24, which is equal to 96. I know that because 20 + 20 + 20 + 20 = 80, and 4 + 4 + 4 + 4 = 16. 80 + 16 = 96 bottles.
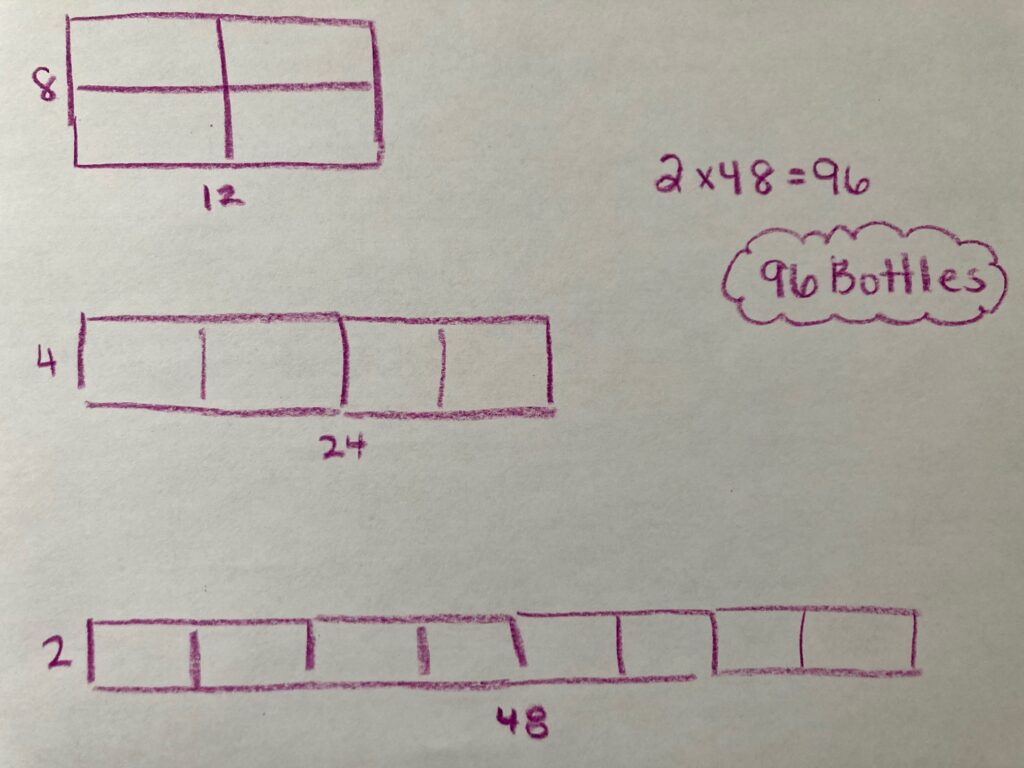
Student Approach #2: Open Array Using Doubling & Halving
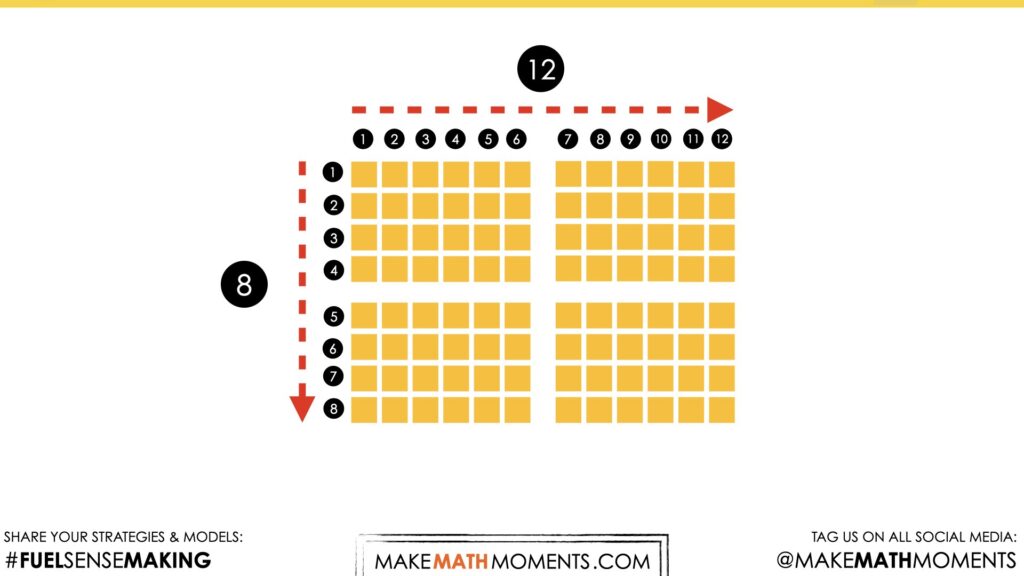
I drew the cases of orange juice how the grocer stocked them on the shelf, two cases by two cases. I knew that there were 8 bottles by 12 bottles. That multiplication is not super easy for me, so I rearranged the cases, 4 cases in a row. Now there are 4 bottles by 24. That was still not easy. I decided to split the cases in half. Once I had 2 bottles by 48 bottles, I could easily double 48, which is 96 bottles.
Student Approach #3: Multiplication with Partial Products
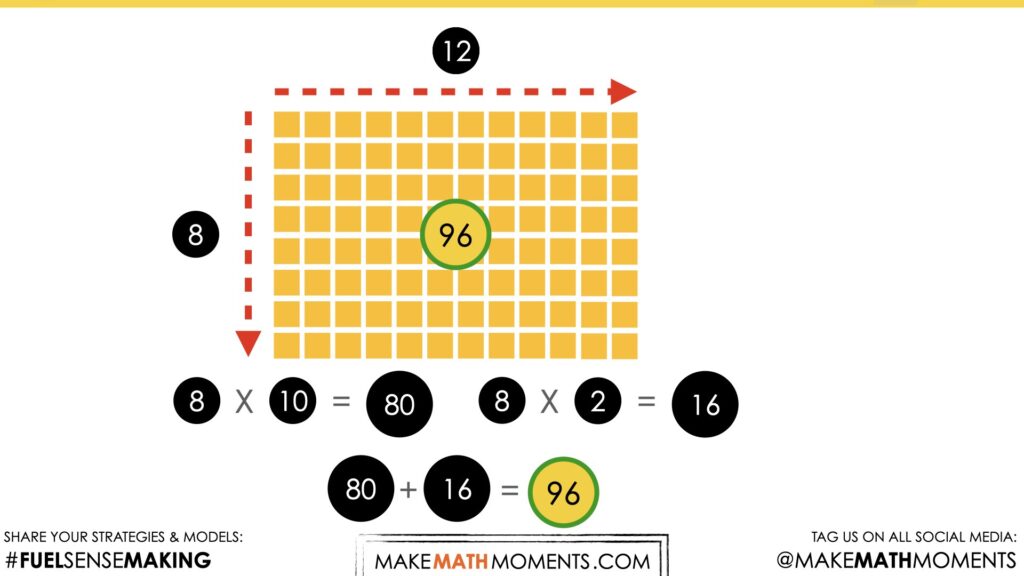
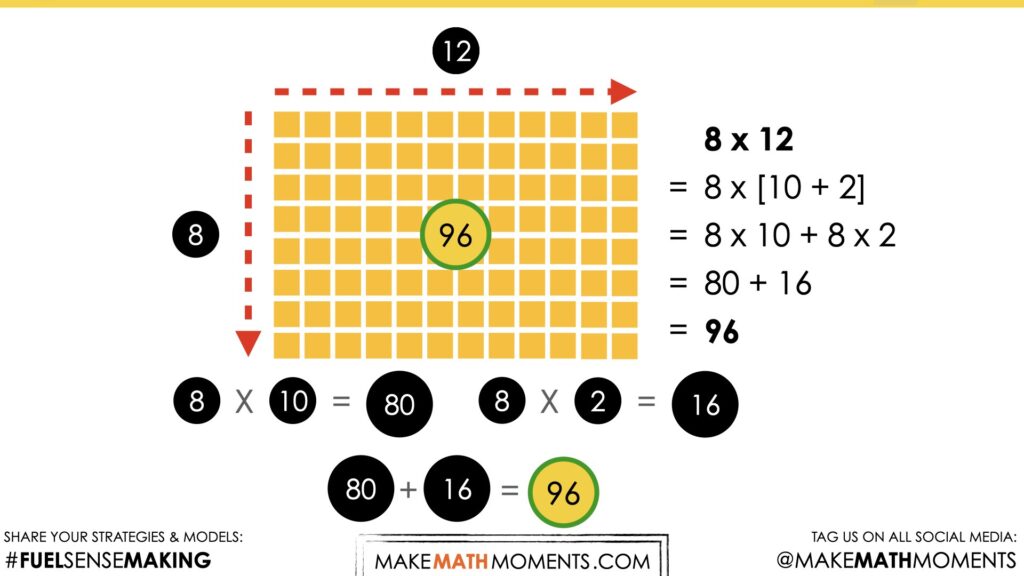
Looking at the array of bottles, I saw that there were 8 groups of 12 bottles. I know that 8 groups of 10 bottles is 80 bottles, and 8 groups of 2 bottles is 16 more. 80 + 16 is 96 bottles of orange juice.
Next Moves
Consolidation
Strategically selecting and sharing student solutions will present an opportunity to explore the properties of multiplication, and three very helpful strategies..
For example, if students attacked the dimensions of bottles in a different order, this is an example of the commutative property.
For example: 8 x 12 = 12 x 8
If students used partial products, this is an example of the distributive property.
For example: 8 x (10 + 2) = 96
In this scenario, the student decomposed the second factor. This is an example of the distributive property over addition.
If students approached this problem through doubling and halving, this is an example of the association property at play.
For example: 8 x 12 = 4 x 24
Highlight that these different strategies, made possible due to the unique properties of multiplication, help us approach multiplication in a way that is easiest for each of us individually.
Consider viewing the following consolidation video to see all the properties at work.
Doubling and Halving
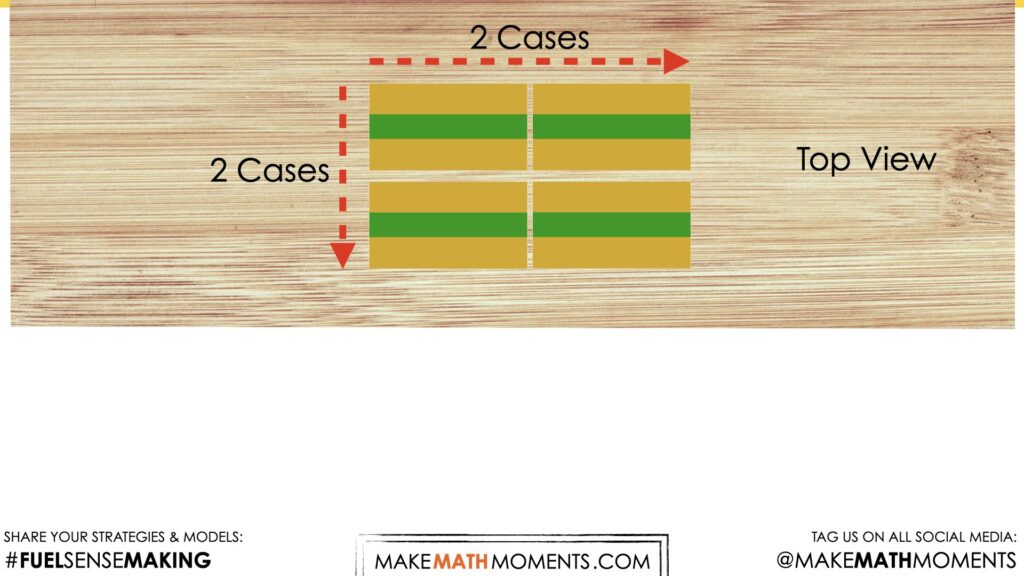
Some students might leverage a doubling and halving strategy to half 8 rows and double 12 columns into a new array arrangement with an equivalent number of bottles, 4 rows of 24 columns.
For some students, they may be able to quickly sum 4 groups of 24 bottles to arrive at a product of 96 bottles. For others, they may leverage the doubling and halving strategy again to arrive at 2 rows of 48 bottles, and possibly again for 1 row of 96 bottles or 96 bottles in total.
Doubling and halving takes advantage of the identity property of multiplication (i.e.: knowing that 1 times a number keeps its identity or remains unchanged) as well as the associative and commutative properties of multiplication (i.e.: dividing a factor into two or more quantities and reassociating them with another factor in the multiplication expression).
In this case, the associative and commutative properties can be leveraged such that:
8 x 12 = 2 x 4 x 12
= 4 x 2 x 12
= 4 x 24
And this process can be repeated until the quantities are favourable enough to be computed mentally.
Another approach can be to use the distributive property of multiplication in order to compose and/or decompose factors to smaller parts that are easier to multiply and then finding the sum.
For example, instead of multiplying 8 rows of 12 bottles, the 12 bottles can be decomposed into 10 + 2 bottles and smaller products or “partial products” can be found and then added together for a total.
This strategy should be modelled symbolically to show students that leveraging the distributive property to create partial products is essentially introducing the use of brackets. In this case, 8 x 12 is equivalent to 8(10 + 2) and the strategy actually violates the popular “BEDMAS” or “PEDMAS” acronym that is falsely taught such that students must always deal with the brackets or parentheses first by adding what is “inside” brackets first rather than simply distributing the factor of 8 to both 10 and 2.
Regardless of which strategy or strategies students leverage in your classroom, be sure to highlight the benefits of each strategy as well as some potential drawbacks of one compared to another in this particular scenario. When might that strategy be better suited for use? When might it be more problematic than helpful? These are great conversations to have with your students and encourage them to debate with each other to realize that some strategies are easier for some than others depending on their past experiences and comfort with particular strategies and models.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering this consolidation prompt to be completed independently.
Consolidation Prompt #1:
Which model and/or strategy shared during today’s consolidation did you find most helpful? Explain.
Consolidation Prompt #2:
Solve the following multiplication problem. Prove that your answer is correct.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!