SPIN TO WIN!
ONE AND TWO INDEPENDENT EVENT PROBABILITY EXPERIMENTS
Explore probability through probability experiments involving one and two independent events of varying complexity.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 3 GAMES
Access each lesson from this unit using the navigation links below
Students will perform a simple probability experiment involving repeatedly spinning a spinner to first predict and then determine which player should win the game.
Intentionality…
As is true for any task, the intentionality or learning objective can vary depending on what mathematical thinking you are hoping to elicit.
This task has a very low floor, but extremely high ceiling by introducing the idea of simple one event probability experiments valid for primary grades or as a warm-up/purposeful practice for middle grades. Then, you can continue building up from this simple one event probability experiment to more challenging scenarios.
Some of the big ideas we will explore through this lesson include:
- We can make predictions about the outcomes of simple probability experiments by thinking of the ratio of successful outcomes to total outcomes as a composed unit and scaling to reveal other equivalent ratios in that proproportional relationship;
- We can make predictions about the outcomes of simple probability experiments by revealing the rate of successful outcomes per trial by partitively dividing the number of successful outcomes possible by the total number of outcomes possible and using the rate to multiply by the number of trials; and,
- As the number of trials in an experiment increase, the outcomes in that experiment will get closer to the outcomes expected theoretically.
Watch Full Video Walk-Thru
Watch the full video walk-thru of this task:
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students this video:
Ask students to engage in a notice and wonder protocol. ANYTHING and EVERYTHING that comes to mind is fair game. Here’s some of the “everything and anything” students noticed and wondered on chart paper:
- I notice a circle with two sections.
- I wonder if this will be used as a spinner for a game?
- I notice this is a fair spinner because both sections are of equal area.
- I wonder if we will be playing a game?
- I notice he colours very fast!
- And many others…
Take some time to acknowledge the noticing and wondering your students have engaged in and try to answer any that you might be able to address right away.
Show this video and ask students if they have any more noticings and wonderings:
Prompt
So we then challenge the students with the question:
Which colour do you predict will win?
**Note that in this version of the game, the first colour cube to make it to the last place on the game board wins.
Challenge students to make a prediction and share with their elbow partners and ensure they attempt convincing them as to why they believe their estimate is reasonable.
Reveal
After allowing students to share their thinking with partners and then with the whole group, we can share what really happened with this video.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Let’s Fuel Sense Making by using the same rules of the game (first cube to the end of the board wins) with different spinners:
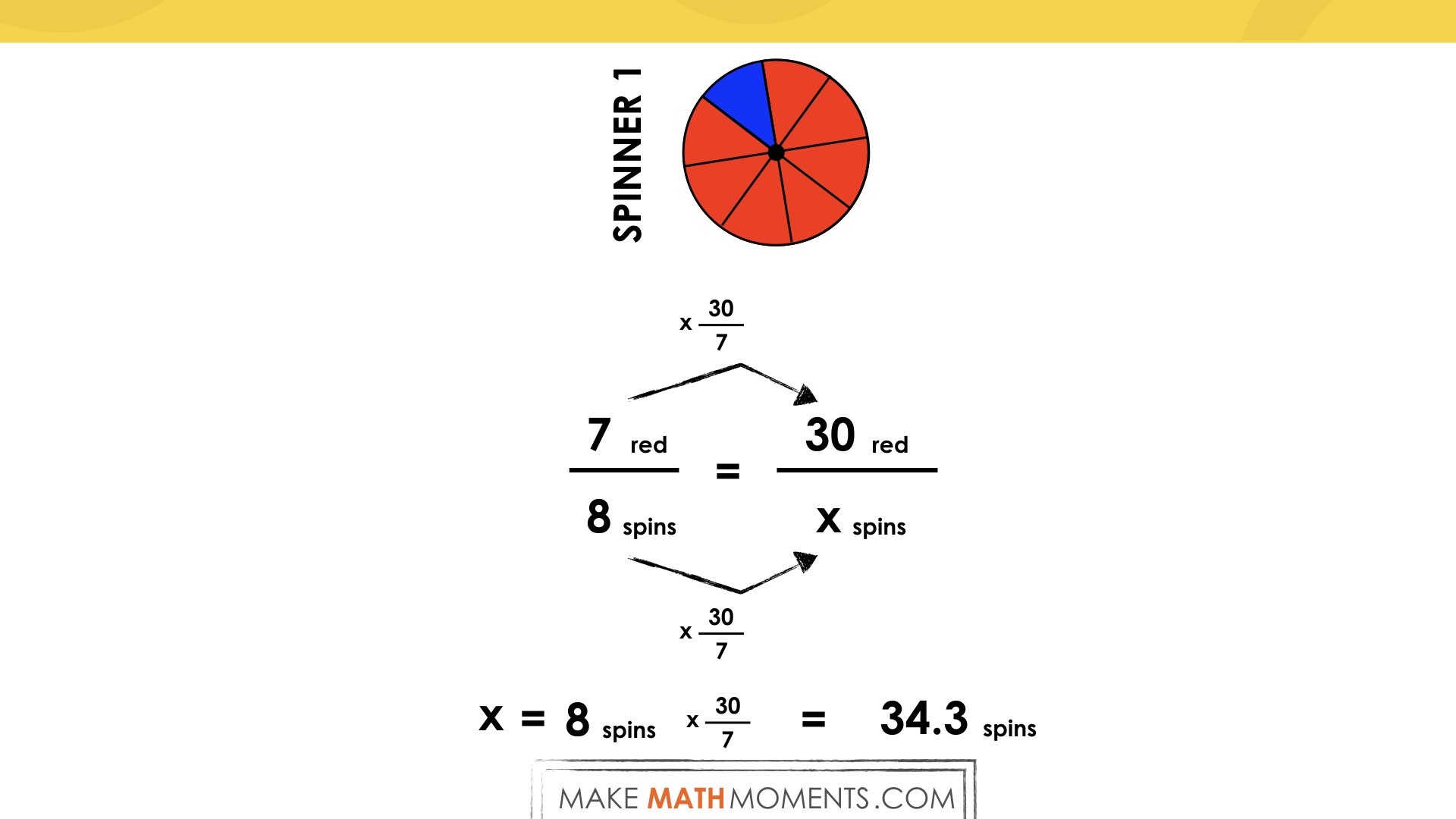
Spinner #1: Watch This…
Using the same rules to the previous game, except use this unfair spinner (1/8 blue, 7/8 red):
Prompt:
Which colour do you predict to win and how many spins will it take?
Allow students time to discuss and convince their neighbours. Encourage them to come up with justification that supports their reasoning.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse.
Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Connecting cubes
- Drawings
- Arrays and/or area models
- Number lines
- Ratio tables
- Symbolic including but not limited to setting up a proportion
Have students share their strategies and reasoning for which colour should win the game.
Ask them to convince you and their peers that their answer is correct by sharing mathematical models.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
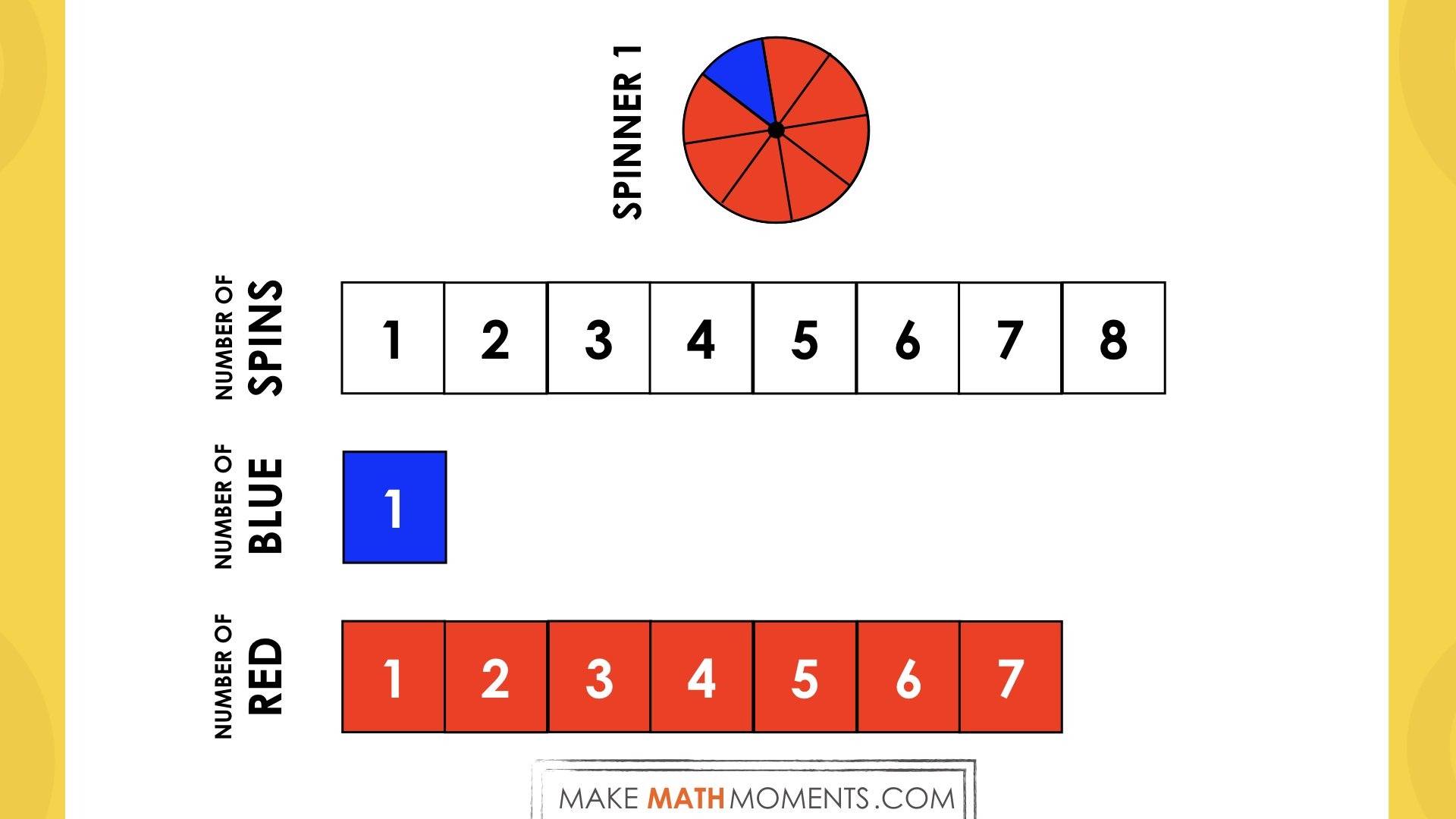
Student Approach #1: Additive Thinking With An Area Model
Students use an area model or tape diagram to represent the part-part whole (i.e.: 1 part blue, 7 parts red make a whole of 8 parts) and use this to repeatedly add or scale through multiplication up to approximately 30 parts red:
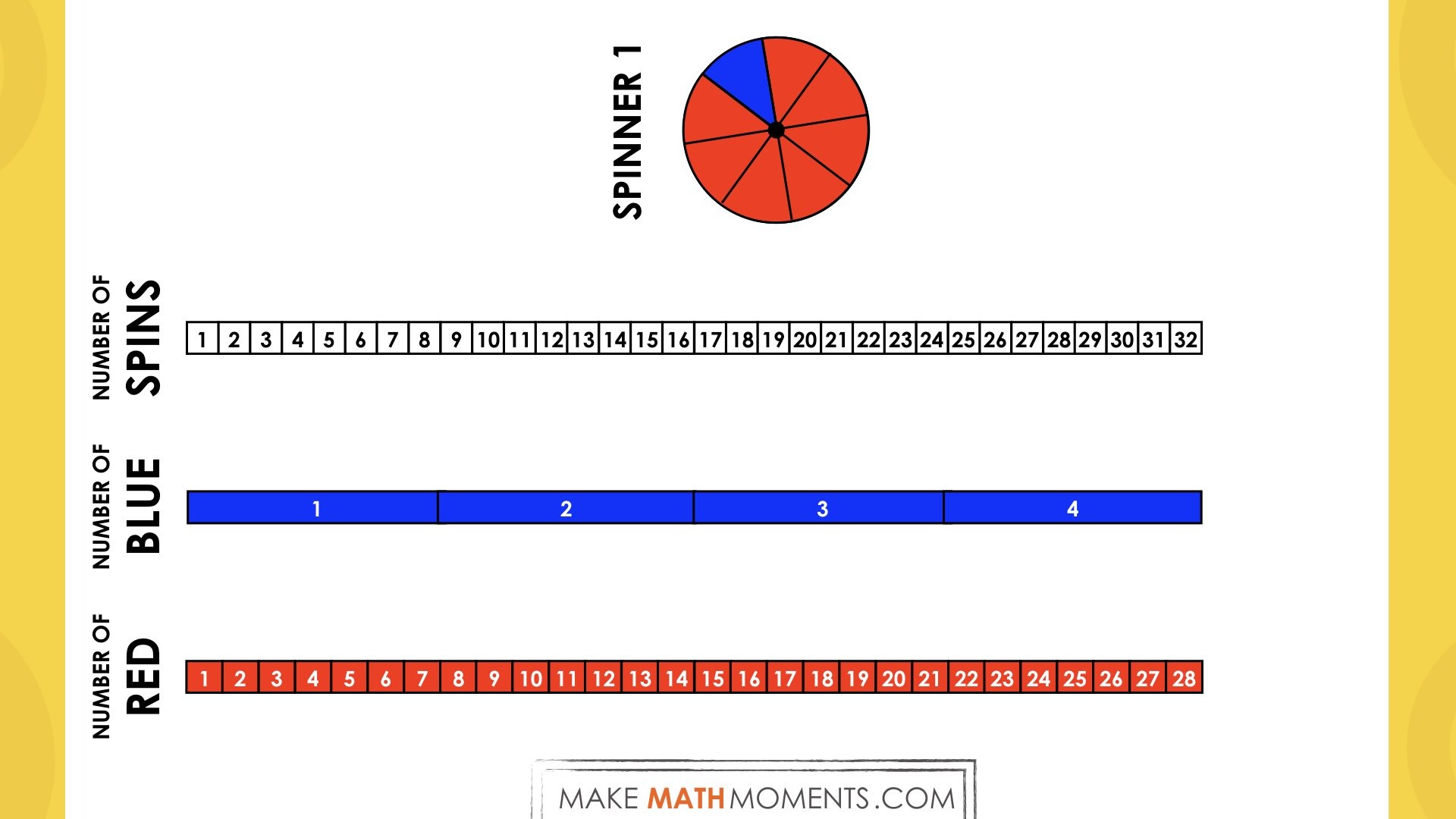
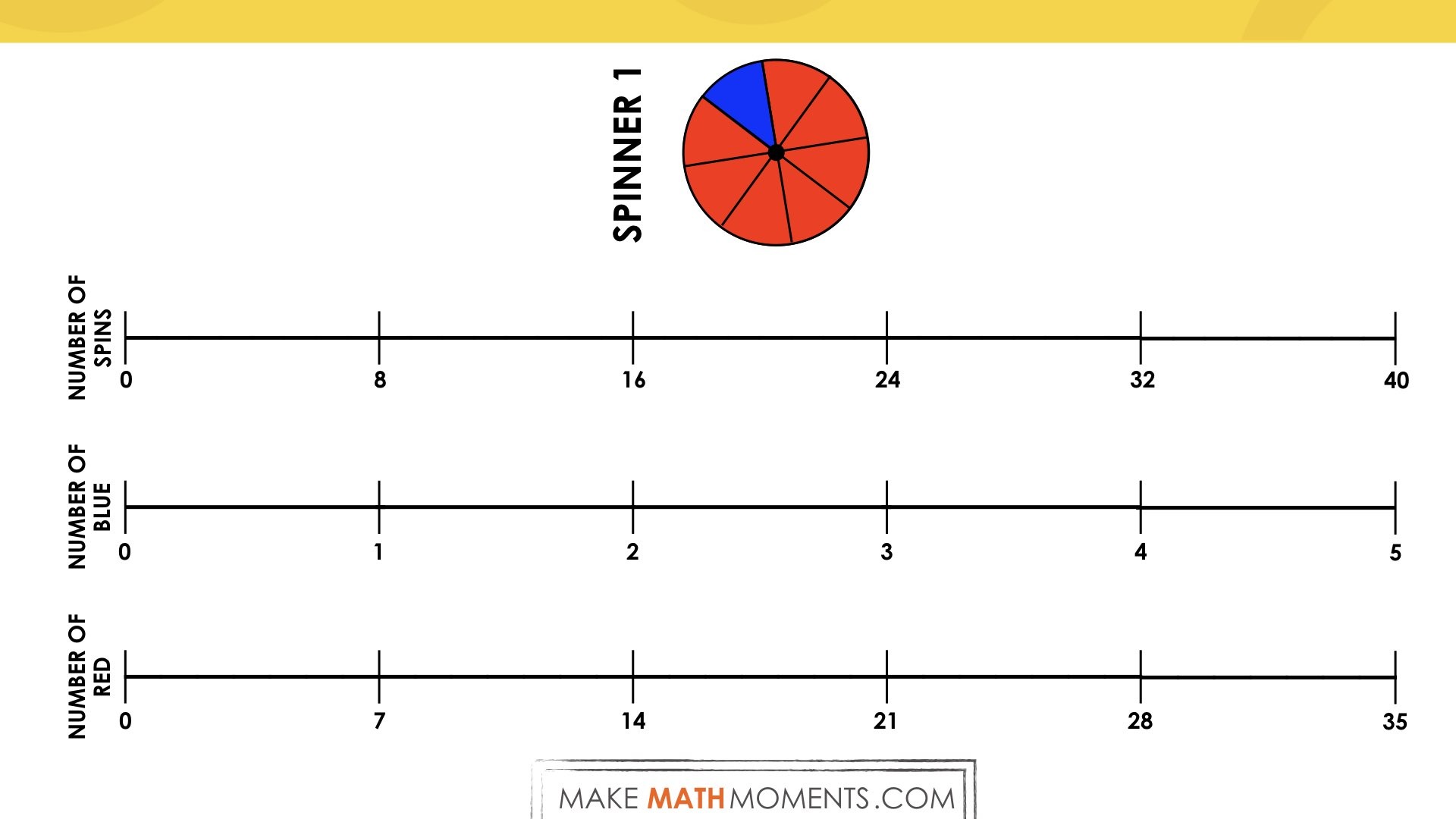
Student Approach #2: Scaling in Tandem With Number Lines
Students use a linear model such as a number line or double number line to represent the blue to red to whole ratio relationship of 1:7:8 and scale up:
Student Approach #3: Scaling in Tandem With A Ratio Table
Students use a ratio table utilizing additive thinking (one-to-one, counting up, skip counting, etc.) or multiplicative thinking (scaling in tandem through doubling, tripling, multiplying by a scale factor, etc.):
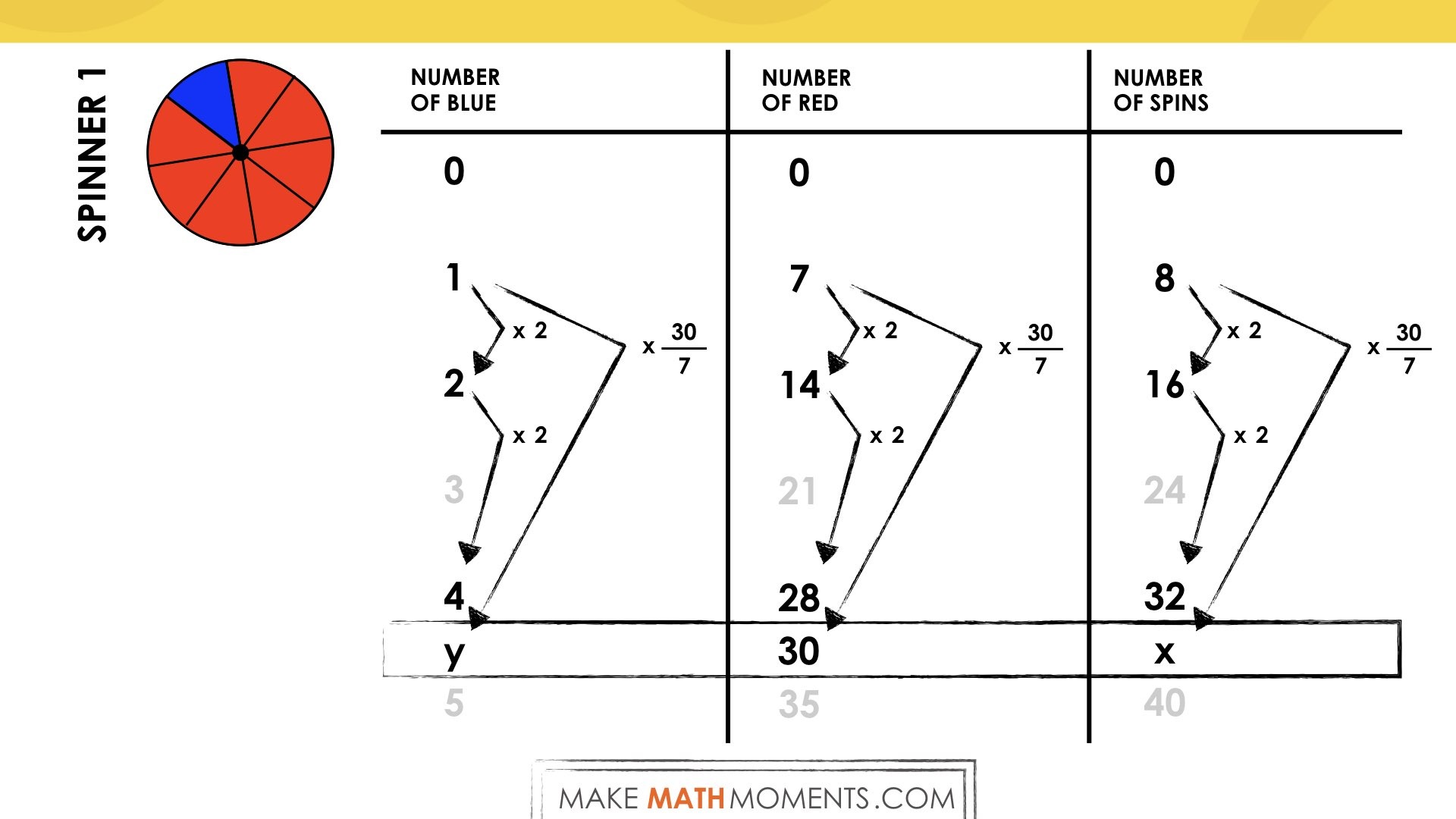
Student Approach #4: Scaling in Tandem With A Proportion
Student creates a proportion of equivalent fractions:
Next Moves
Reveal 2
After students have had the opportunity to discuss their solution strategies with their partners/groups, solution strategies have been selected, sequenced, and shared to the group for the teacher to make connections with, you can share the second reveal video:
Consolidation
If students have not been explicitly pre-taught algorithms and procedures including the idea that the area relative to the whole of a spinner for a particular colour will provide the rate at which a colour should come up per spin (i.e.: a spinner equi-partitioned in halves will produce a rate of half a red per spin and half a blue per spin), it is likely you’ll see a lot of additive thinking and possibly multiplicative thinking to “scale up” the number of spins to the number of total squares on the game board.
If students are additively scaling up by repeatedly adding quantities such as adding 1 blue for every 7 red, consider nudging students to think multiplicatively without forcing or funnelling them.
For example, you could ask students:
What might happen if you were to double those values?
Would it still work?
As you consolidate, be sure to highlight additive thinking and work your way to multiplicative thinking to scale up.
Finally, be sure to highlight any students who may have discovered (or previously encountered) rate reasoning by simply multiplying the number of spins by the fraction of the spinner representing a specific colour. For example, the area coloured blue represented 1/8 of the spinner and thus we can multiply the number of spins by 1/8 to determine the expected number of times blue should come up on the spinner.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering this consolidation prompt to be completed independently.
Consolidation Prompt:
After playing the Spin to Win game with the various spinners, explain what you’ve learned about the probability of winning the game when a spinner is partitioned into different sized parts.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Extend
Extend this task using the same rules from the original game, but using different spinners.
Each of the spinners has a Reveal Video in the Extend tab to show what really happened.
Revisit the student answers. Have students discuss their thinking and what they would change if they did the task again. Return to the questions you recorded from your list of student Noticing and Wondering and answer any questions that have not been answered.
Resources & Downloads
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!