SOWING SEEDS

Whole Number Partitive and Quotative Division (1 & 2-Digit)

Introduction to partitive and quotative division. This unit is designed to support students in understanding the two types of division and should be considered before exploring all other division units.

Intentionality

Spark Curiosity

Fuel Sensemaking

During Moves

Student Approaches

Consolidation

Reflect and Consolidation Prompts

Resources & Downloads

Educator Discussion Area

Teach This Lesson

Facilitate this lesson with students!
PRESENTATION MODE

Intentionality & Unit Overview

Length of Unit: 5 Days

Access each lesson from this unit using the navigation links below

DAY 1
DAY 2
DAY 3
DAY 4
DAY 5

Students will determine the number of pea seeds that can be planted per pot.

Intentionality…

In this task, students will determine the total number of peas to sow per pot. In this partitive context, the students will likely fair share the total quantity of peas amongst the 6 pots in order to determine the number of peas in every pot.

Some of the big ideas that may emerge through this task include:

  • There are two types of division;
  • Partitive division is when the total quota is known (the dividend), and the number of parts or groups (the divisor) is known;
  • Partitive division reveals a rate;
  • In partitive division, the dividend and the divisor often have different units;
  • The dividend and the divisor of any division sentence represent a ratio;
  • In a partitive context, the ratio is often a composed unit;
  • The dividend from any division sentence can be decomposed into smaller parts to allow for friendlier division by the divisor. This strategy is known as partial quotients. (i.e.: 85 ÷ 5 = 45 ÷ 5 + 40 ÷ 5 = 9 + 8 = 17).

Spark Curiosity

What Do You Notice? What Do You Wonder?

Show students the following video:

Then, ask students:

What do you notice?

What do you wonder?

Give students 60 seconds (or more) to do a rapid write on a piece of paper.

Replaying the video and/or leaving a screenshot from the video up can be helpful here.

Sowing Seeds [Day 1] - Planting Peas - 02 - SPARK IMAGE - Notice Wonder.001

Then, ask students to share with their neighbours for another 60 seconds.

Finally, allow students to share with the entire group. Be sure to write down these noticings and wonderings on the blackboard/whiteboard, chart paper, or some other means to ensure students know that their voice is acknowledged and appreciated.

Some of the noticing and wondering that may come up includes:

  • There was a pot.
  • I noticed a package of peas.
  • I wonder what is going on here?
  • It looks like they are going to plant peas in a gardening pot.
  • And many more.

At this point, you can answer any wonders that you can cross off the list right away. For example:

  • Yes, this person is in fact planning to plant the seeds in small gardening pots.
  • The package had quite a few seeds in it, but we aren’t sure how many there are.
  • And so on.

Estimation: Prompt

After we have heard students and demonstrated that we value their voice, we can land on the first question we will challenge them with:

How many peas were poured into the container?

Make an estimate.

Sowing Seeds [Day 1] - Planting Peas - 03 - SPARK ESTIMATE IMAGE PROMPT.001 (1)

We can now ask students to make an estimate (not a guess) as we want them to be as strategic as they can possibly be. This will force them to determine a number of peas that would be reasonable before determining a more precise answer. Consider asking students to think about a number of peas that would be “too low” and a number that would be “too high” before asking for their best estimate in order to help them come up with a more reasonable estimate. Encourage students to share their estimates, however avoid sharing their justification just yet. We do not want to rob other students of their thinking.

Estimation: Update & Partial Reveal

Show students the following video:

Ask students to update their estimate.

Sowing Seeds [Day 1] - Planting Peas - 05 - SPARK UPDATE ESTIMATE IMAGE.019

Facilitator Note:

Be sure to reiterate that we are not leveraging the help of a calculator here as we are always trying to give students an opportunity to build their fluency and flexibility with operations by leveraging strategies and mathematical models.

While students are updating their estimate, listen and observe as students work to make updates. What strategies and mathematical models are students leveraging? Are they:

  • Counting by ones?
  • Skip counting?
  • Repeatedly adding?
  • Using spatial reasoning?
  • Using an algorithm?

Sowing Seeds [Day 1] - Planting Peas - 07 - SPARK ESTIMATE REVEAL IMAGE.001

Celebrate student estimates that were very close to the actual number of peas using a routine of your choice as we head into the sense making portion of this lesson.

Fuel Sense-making

Crafting A Productive Struggle: Prompt

Now that we have confirmed that there are 78 peas to be planted, prompt students by stating:

All the peas that are shown will be sown in six pots. We want to ensure that every pot has the same number of peas. How many peas should be sown in each pot?

Sowing Seeds [Day 1] - Planting Peas - 08 - SENSE MAKING PROMPT IMAGE.001 (1)

Be sure to remind students that they are not to use a calculator to determine the number of peas per pot as using that tool will rob them of this mathematical experience. Students should use a mathematical model in order to communicate their thinking.

During Moves

While Students Are Productively Struggling…

Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:

  • most accessible to least accessible solution strategies and representations;
  • most common/frequent to least common/frequent strategies and representations; or,
  • choose another approach to selecting and sequencing student work.

The tools and representations you might see students using to convince their peers and/or the teacher include:

  • Concrete manipulatives to fairly distribute the peas
  • An array through skip counting
  • An open-array using partial products
  • A flexible algorithm using partial products

Have students share their strategies and reasoning for how to represent the number of peas per pot. Ask them to convince you and their peers that their answer is correct by sharing mathematical models.

Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.

Student Approaches

Student Approach #1: Pictorial Fair Sharing with Counting

MMM - Sowing Seeds - Day 1 - 01

I drew 6 circles to represent the pots. I knew that I had to share the peas between those pots. Putting one pea in at a time would take too long, so I started with five peas. I counted by five: 5, 10, 15, 20, 25, 30. I thought I could put five more peas. 35, 40, 45, 50, 55, 60. I tried putting in five peas again, but that was too many. So I started to place one pea at a time. I had six more, that was 66. Another six, that was 72. And finally six more, and I had all 78 peas.

Student Approach #2: Array Using Repeated Addition

MMM - Sowing Seeds - Day 1 - 02

I drew the six pots along the side. I started by putting one pea in each pot. I kept doing this, adding 6, until I had all 78 peas. I needed to place 13 peas in each pot.

Student Approach #3: Open-Array Using Partial-Products and Revealing Partial-Quotients

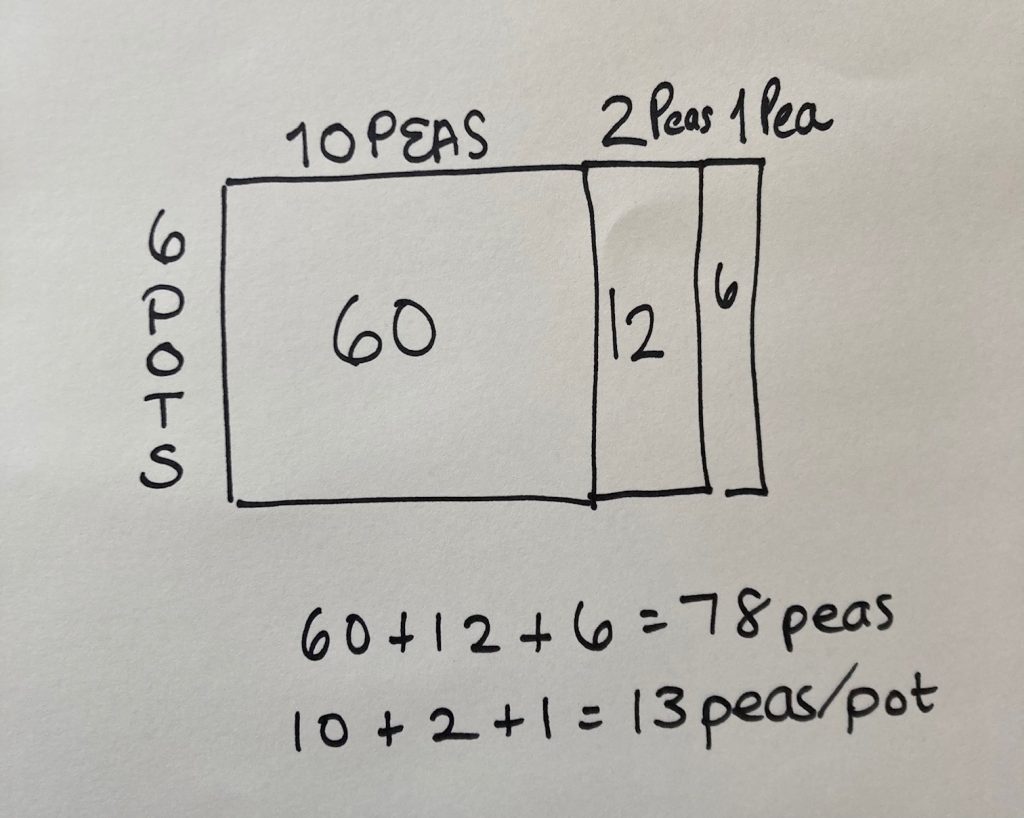
MMM - Sowing Seeds - Day 1 - 03

I know that if I put 10 peas in every pot, that will use 60 of my total peas. I added two more to each pot, that’s 72 peas. So then I knew I had to add one more pea to every pot in order to use all of the 78 peas.

Next Moves

Reveal

Show students the following reveal video:

Or consider sharing the final screenshot of the video:

Sowing Seeds [Day 1] - Planting Peas - 10 - NEXT MOVES - REVEAL IMAGE.001

Answer: 13 Peas per Pot

Consolidation

You might consider selecting student solutions that shift students from the set model (six circles and placing peas one at a time) towards an array model that promotes skip counting.

You can see this modelled below in the reveal video:

The array, and eventually the open array, are powerful tools for solving division problems using the partial quotient strategy.

See this in the silent solution consolidation video below:

Sowing Seeds [Day 1] - Planting Peas - 12 - NEXT MOVES - CONSOLIDATION SILENT SOLUTION IMAGE.001

At this point, it is a great idea to ask students the following prompt.

Prompt:

What operation did you use to solve this problem?

Give students the opportunity to turn and talk, and then share some of their thinking. Some students may say that they used counting, addition, subtraction, multiplication or division depending on their strategy.

At this point, students may or may not have realized that this context can be represented by a division sentence. This is your opportunity to name this behavior as division. In particular, partitive division.

78 peas ÷ 6 pots = 13 peas/pot

It is important to highlight the units in this division sentence. Notice that the dividend is peas, the divisor is pots, and the quotient is peas per pot (peas/pot), a rate.

Ask students to share a few other division scenarios like this one where the dividend and the divisor represent a ratio with two different units.

For example, candies to people, apples to baskets, eggs to cartons…

Reflect and Consolidation Prompts

Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.

Consolidation Prompt #1:

Today’s context was an example of partitive division. In your own words, explain what partitive division is.

Consolidation Prompt #2:

Which model and/or strategy shared during today’s consolidation did you find most helpful? Explain.

Consolidation Prompt #3:

Create your own partitive division context like we did with the seeds and the pots from today’s lesson.

Solve your problem and be sure to clearly indicate your strategy and model to convince others of your thinking.

We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.

Resources & Downloads

Printable Lesson Plan PDF

Videos, Images & Media Files

Apple Keynote Presentation

Powerpoint Presentation

Printable Consolidation Prompts

Educator Discussion Area

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

Explore Our 60+ Problem Based Units

This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.

Dig into our other units of study and view by concept continuum, grade or topic!

EXPLORE UNITS

Get Tasks, Tips & Tools To Your Email!

__CONFIG_colors_palette__{"active_palette":0,"config":{"colors":{"30800":{"name":"Main Accent","parent":-1},"f2bba":{"name":"Main Light 10","parent":"30800"},"trewq":{"name":"Main Light 30","parent":"30800"},"frty6":{"name":"Main Light 45","parent":"30800"},"flktr":{"name":"Main Light 80","parent":"30800"}},"gradients":[]},"palettes":[{"name":"Default","value":{"colors":{"30800":{"val":"rgb(59, 136, 253)","hsl":{"h":216,"s":0.98,"l":0.61}},"f2bba":{"val":"rgba(59, 136, 253, 0.1)","hsl_parent_dependency":{"h":216,"s":0.98,"l":0.61,"a":0.1}},"trewq":{"val":"rgba(59, 136, 253, 0.3)","hsl_parent_dependency":{"h":216,"s":0.98,"l":0.61,"a":0.3}},"frty6":{"val":"rgba(59, 136, 253, 0.45)","hsl_parent_dependency":{"h":216,"s":0.98,"l":0.61,"a":0.45}},"flktr":{"val":"rgba(59, 136, 253, 0.8)","hsl_parent_dependency":{"h":216,"s":0.98,"l":0.61,"a":0.8}}},"gradients":[]},"original":{"colors":{"30800":{"val":"rgb(59, 136, 253)","hsl":{"h":216,"s":0.98,"l":0.61}},"f2bba":{"val":"rgba(59, 136, 253, 0.1)","hsl_parent_dependency":{"h":216,"s":0.98,"l":0.61,"a":0.1}},"trewq":{"val":"rgba(59, 136, 253, 0.3)","hsl_parent_dependency":{"h":216,"s":0.98,"l":0.61,"a":0.3}},"frty6":{"val":"rgba(59, 136, 253, 0.45)","hsl_parent_dependency":{"h":216,"s":0.98,"l":0.61,"a":0.45}},"flktr":{"val":"rgba(59, 136, 253, 0.8)","hsl_parent_dependency":{"h":216,"s":0.98,"l":0.61,"a":0.8}}},"gradients":[]}}]}__CONFIG_colors_palette__

MAKE MATH MOMENTS ACADEMY

A membership community aimed to accelerate your professional learning journey by supporting mathematics educators as they elevate their pedagogical practice and build their math content knowledge.

Get Started

MEMBER AREAS

CONTACT US

Facebook Twitter Instagram Youtube Spotify
JOIN FREE FOR 30 DAYS