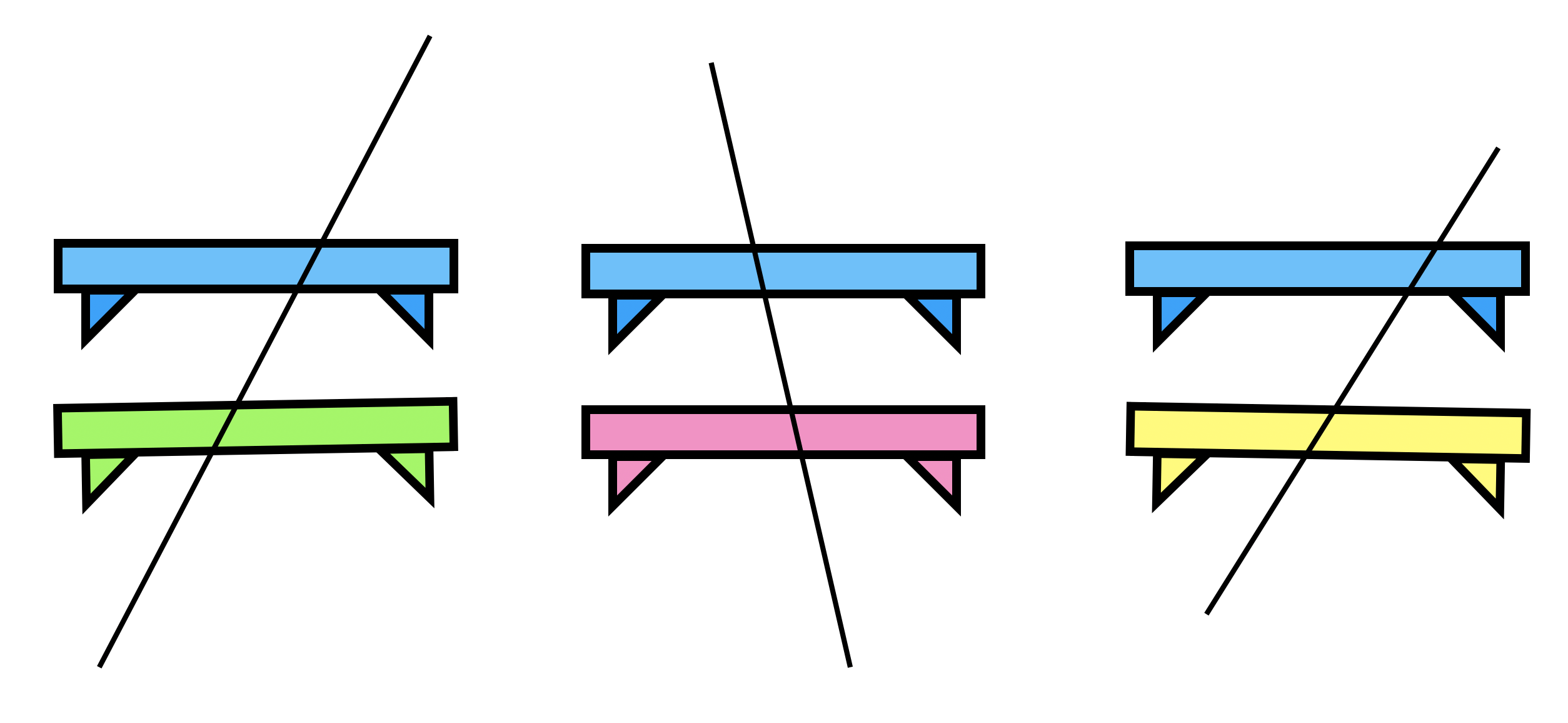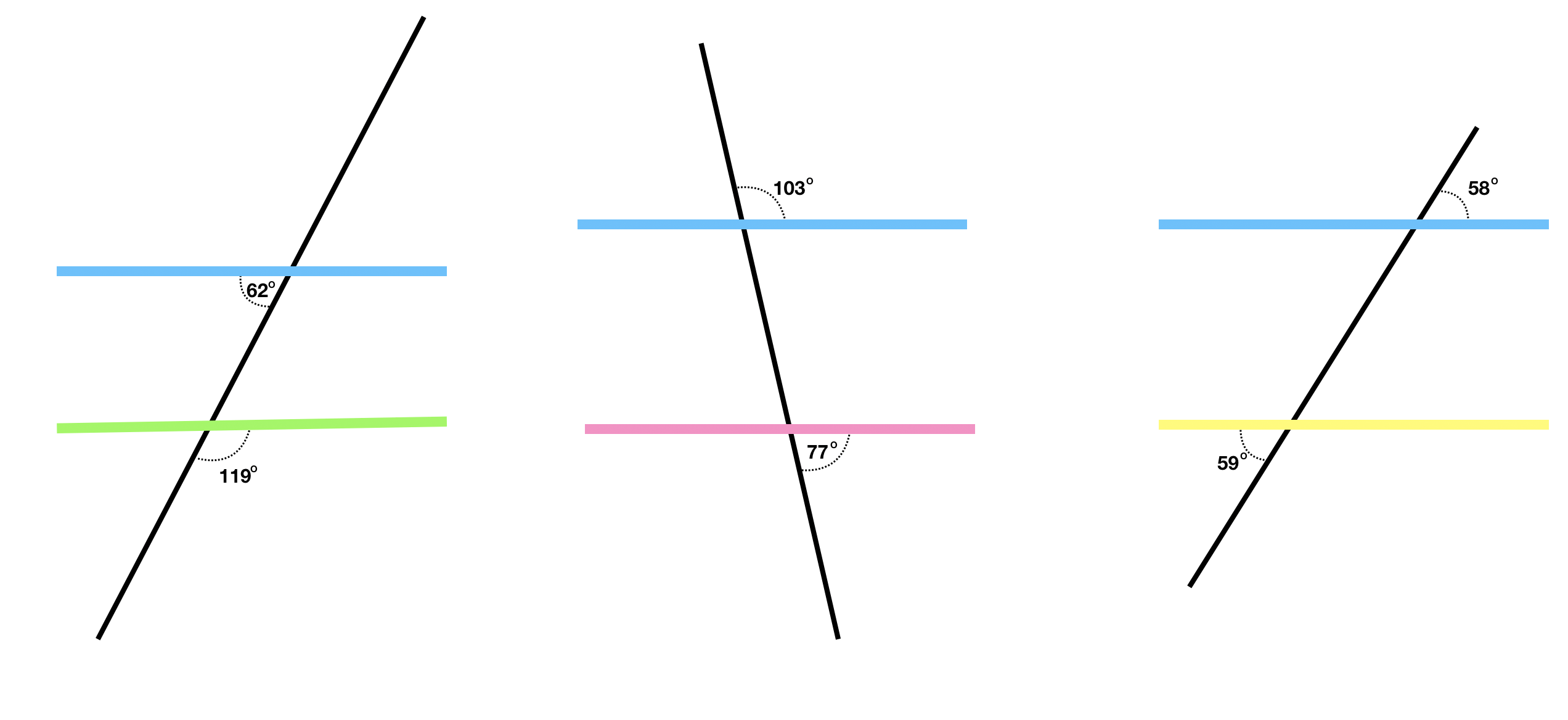SLIDING SHELVES
PARALLEL LINES AND TRANSVERSAL LINES
Investigate and construct understanding of angle relationships related to parallel lines and transversal lines.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview
Current Length of Unit: 1 Day*
*This lesson is the first of an expected 5-day unit. The remaining four (4) days will be released as soon as they are available.
Students will investigate and construct understanding of the angle relationships that exist between parallel lines and transversal lines.
Intentionality…
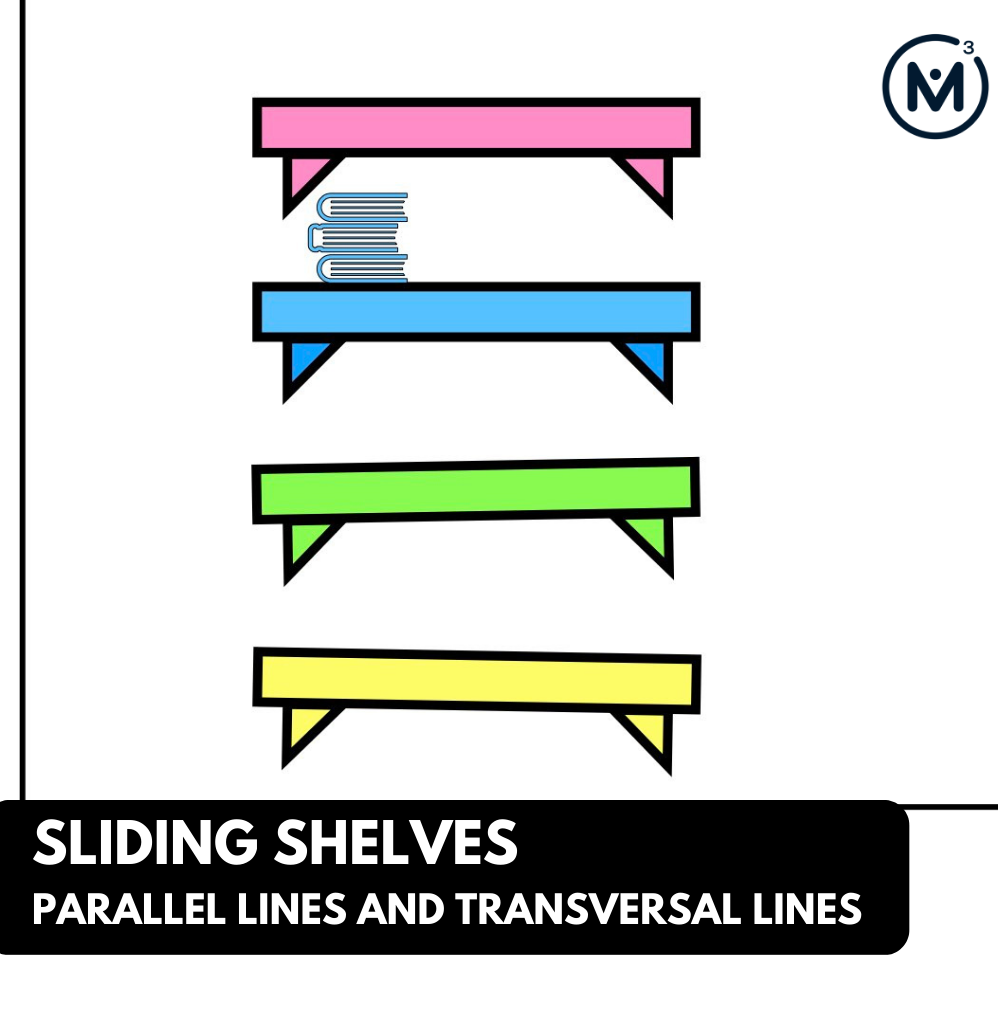
Students will explore angle relationships that exist between parallel lines and transversal lines to decide which shelves are parallel.
Big ideas that will be uncovered include:
- Any set of two or more lines that never meet are considered to be parallel;
- The distance between each pair of parallel lines never changes; and,
- Any transversal line intersecting two or more lines that are parallel will produce angle relationships that can be used to find missing angle measures.
Spark Curiosity
What Do You Notice? What Do You Wonder?
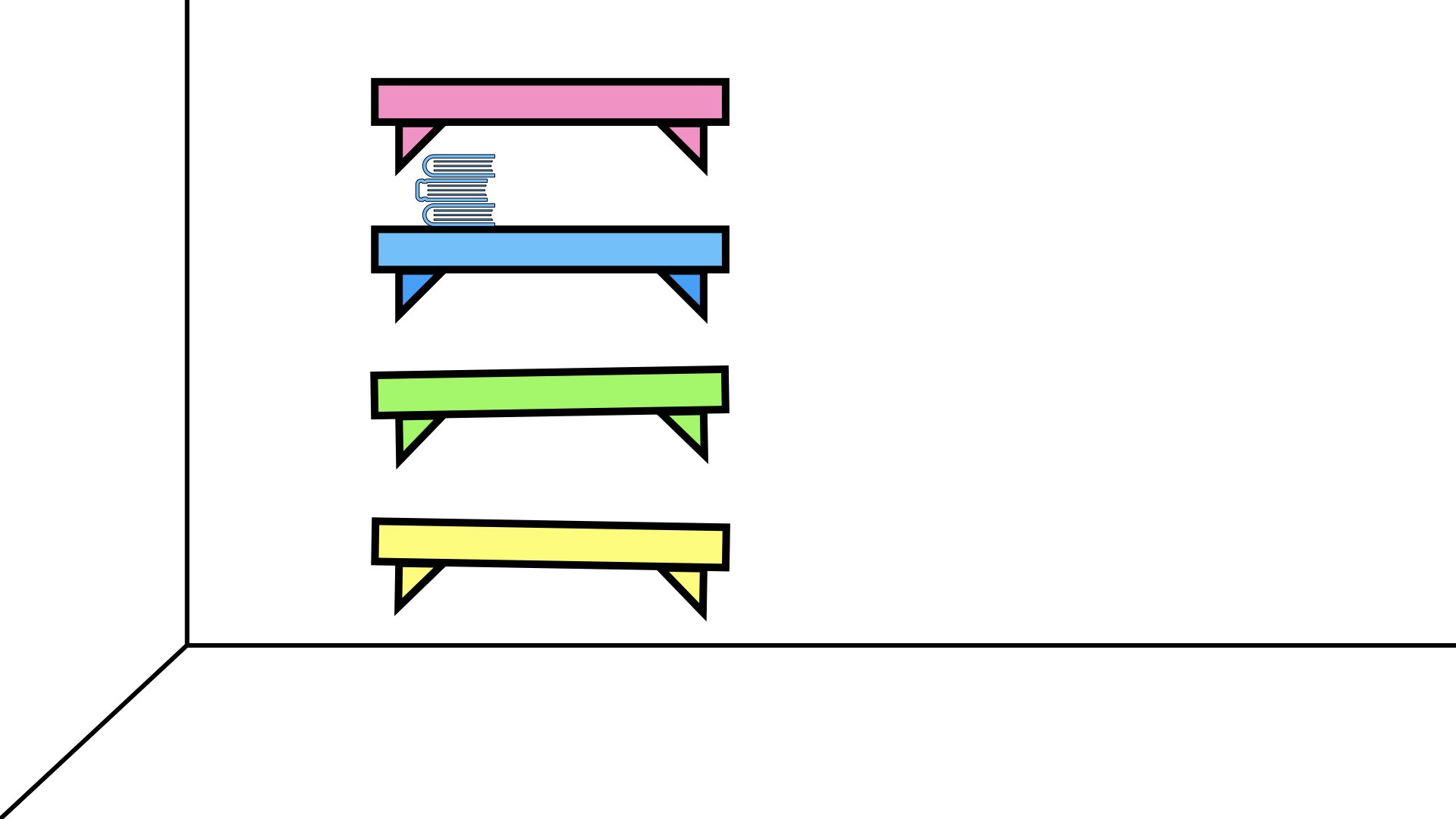
Show students the video of 4 shelves being hung on a wall. Some shelves look parallel to one another and some do not.
Ask students to engage in a notice and wonder protocol. ANYTHING and EVERYTHING that comes to mind is fair game.
Write down all of the student noticing and wondering. For example:
- I noticed four shelves.
- It looks like some shelves are slanted.
- I wonder if the books would slide off some of the other shelves?
- I wonder if the shelves are level?
- And many others…
Take time to acknowledge the noticing and wondering your students have engaged in and try to answer any that you can address right away.
Prompt: Set The Context & Estimate
Then, pose the following question:
Which shelves are parallel?
Make an estimate.
Have students estimate which shelves appear to be parallel. A discussion about what makes two lines parallel might be useful and/or necessary.
Record those estimates on the black/whiteboard or on chart paper.
Digging Deeper
Show an image of each of the shelves paired with the blue (level) shelf.
Ask students:
The blue shelf is level.
What is needed if we are to prove which shelves are parallel to the blue shelf and which are not?
Students may say:
- Use a level.
- Measure the height from the ground along different points on each shelf.
- Put the books on the shelf and see if they slide off.
- Measure the angles the shelves make compared to each other.
Fuel Sense-making
Prompt: Update Your Estimate
Now that students have shared some of the ways they might go about determining which shelves are parallel to the blue shelf, we can ask them:
What is needed if we are to prove which shelves are parallel to the blue shelf and which are not?
Essentially we want to have students think critically about what information would help them make their argument.
At this point, show students this image and ask them:
How this might this image be helpful?
Lead students in a discussion on why measuring angles may be a more efficient and accurate way to determine if the shelves are parallel compared to some of the responses students may have shared previously in the discussion (i.e.: measuring from the ground to two different points on the shelf or putting books on the shelf to see if they slide off).
A big idea we want students to walk away with is that a transversal line provides an opportunity to easily compare whether two or more lines are parallel.
If we withhold the angle measurements on this image then the class can have a conversation around this question:
What is the least amount of angle measurements needed to determine if the shelves are parallel?
For example:
In each diagram if one angle is revealed, is that enough information to determine if the shelves are parallel?
Why or why not?
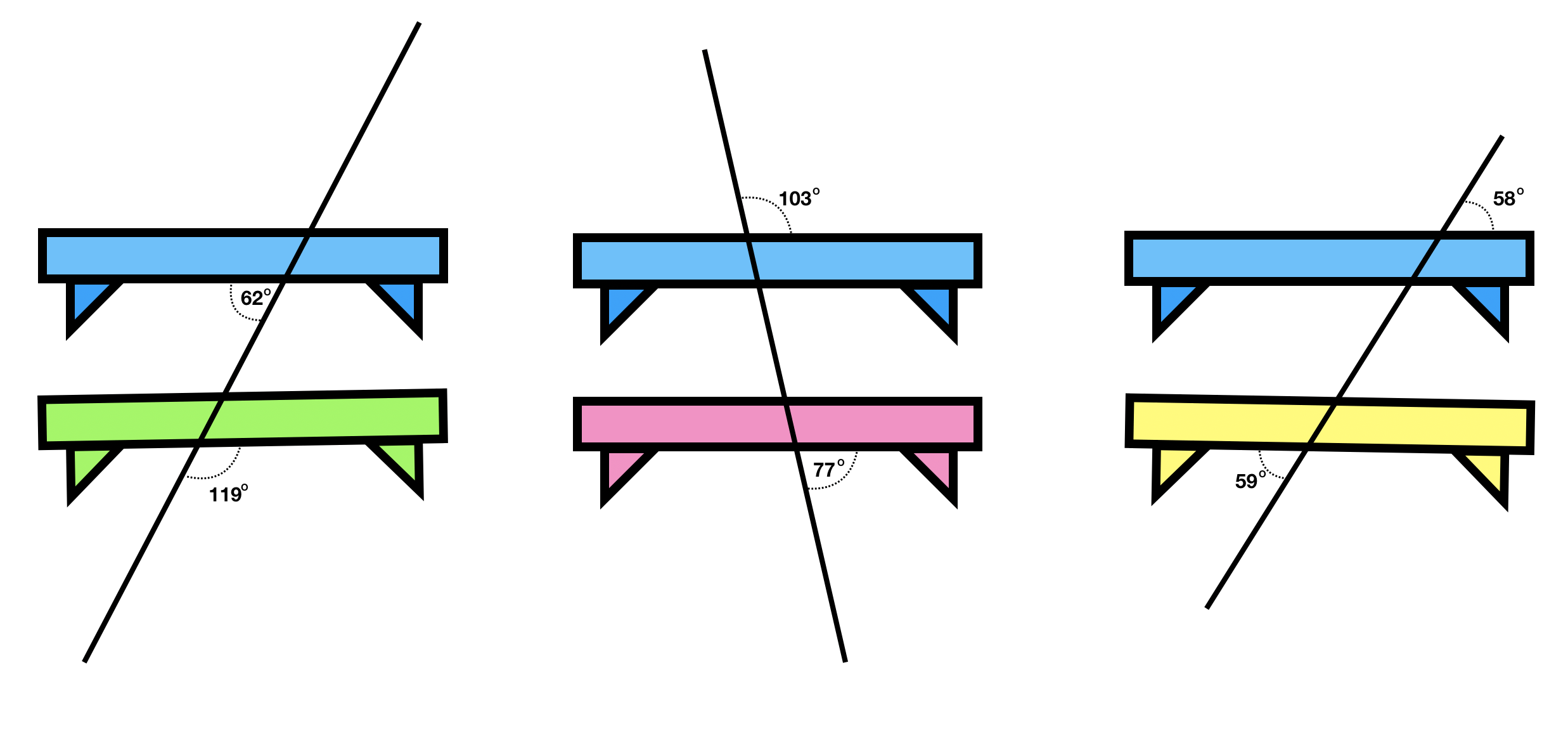
Show students this image (or pass out this image on a page):
Optional: Use this image instead.
Allow students to use the given information to determine which shelves are parallel to the blue shelf.
During Moves
While Students Are Productively Struggling….
Monitor student thinking by circulating around the room and listening to the mathematical discourse.
Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
Have students share their strategies and reasoning for determining which shelves are parallel to the blue shelf. Ask them to convince you and their peers that their answer is correct by sharing mathematical reasoning.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Facilitator Notes
If students are having difficulty getting started, encourage them to use a protractor to measure the angles formed. Using the protractor can be a good starting point for students because it can help lead toward answering the big question as well as leading toward a discussion on the possible error that occurs when measuring.
Student Approaches
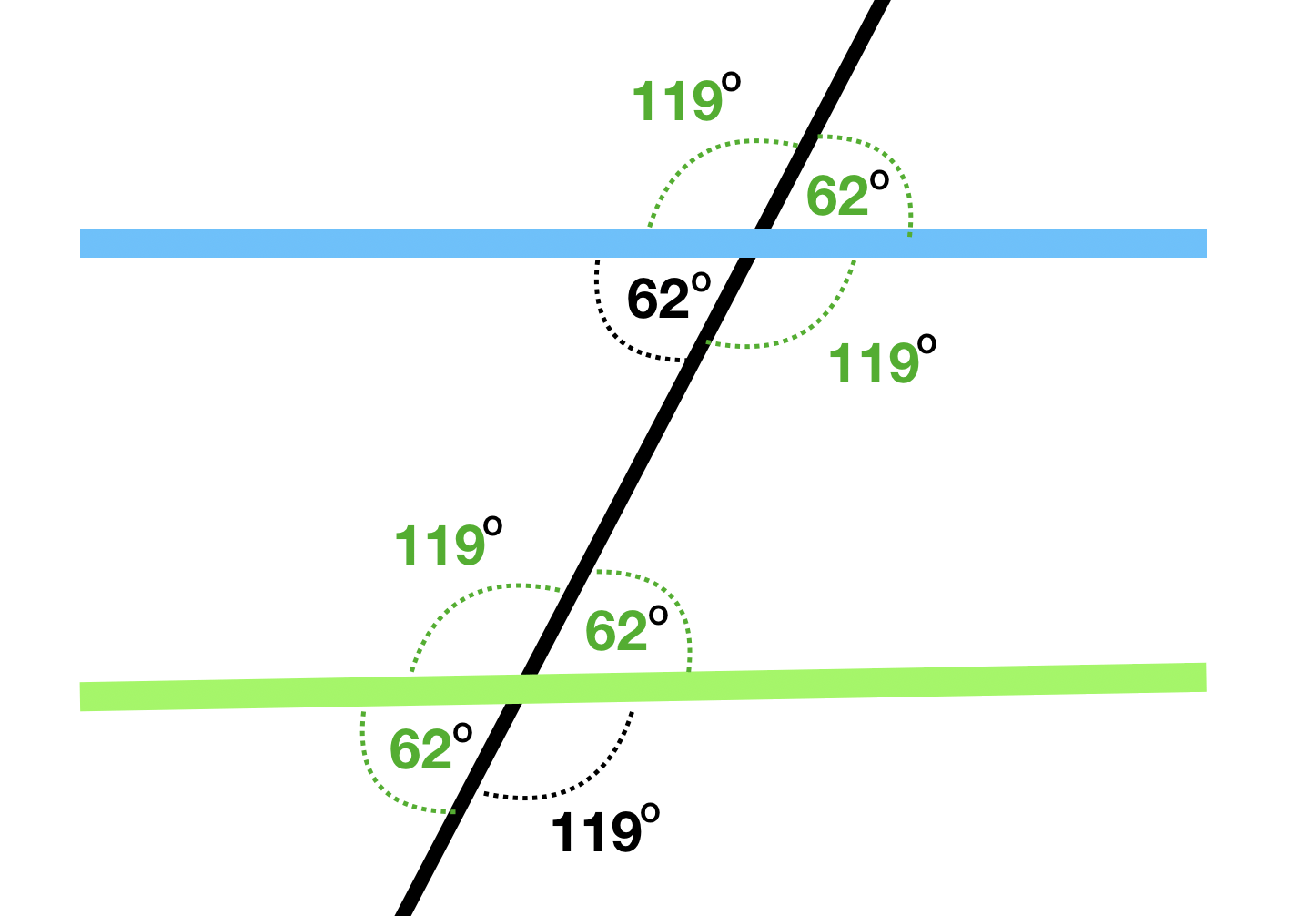
Student Approach #1: Corresponding Angles
Strategy
I used a protractor and measured each of the angles the shelves make with the transversal and I found that the green shelf was not parallel because each of the corresponding angles should have been identical if they were parallel. (a similar strategy is used to prove that the pink shelf is parallel and the yellow shelf is not parallel).
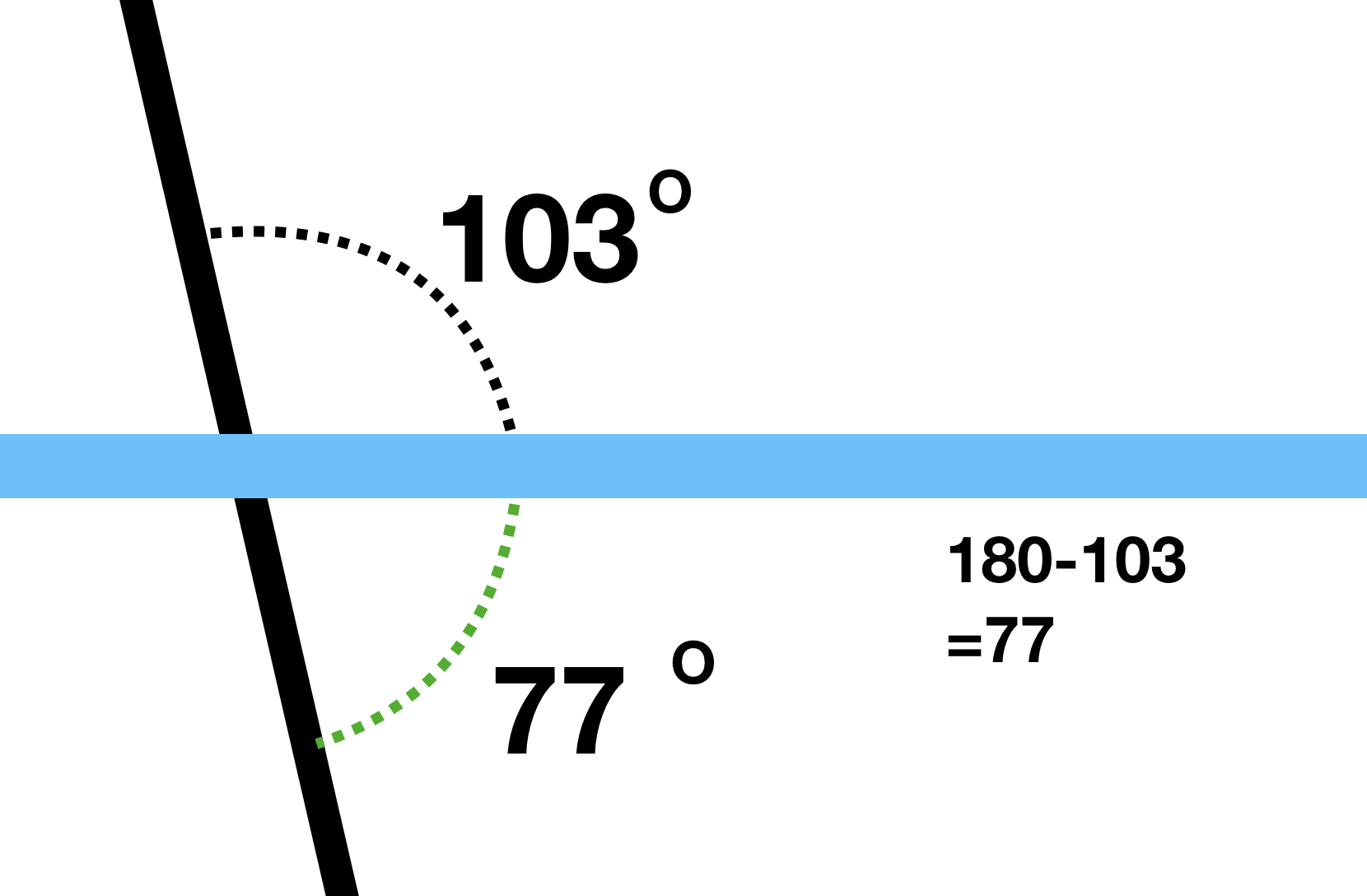
Student Approach #2: Straight, Opposite & Corresponding Angles
Strategy
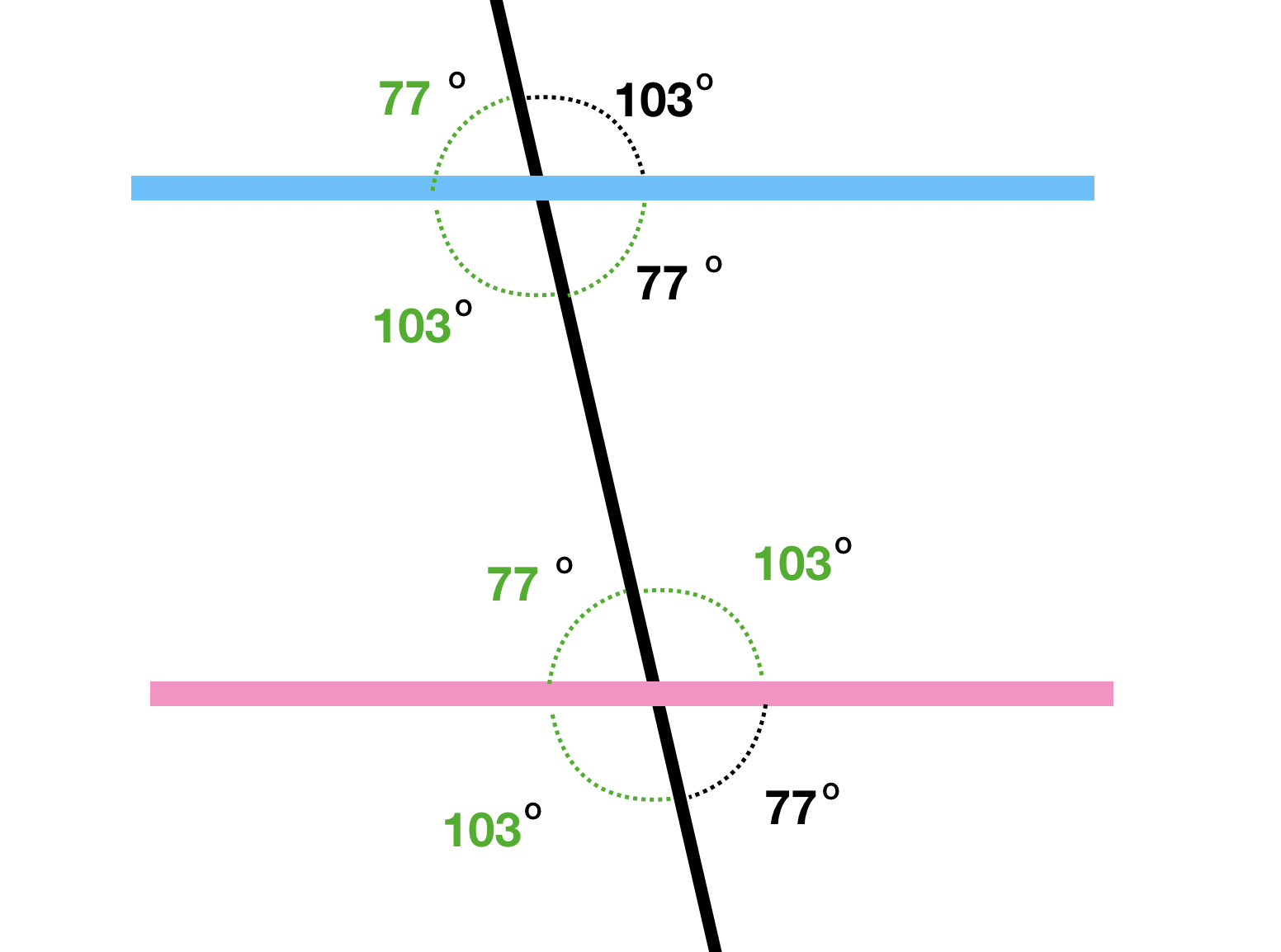
I used the fact that measuring from one side of a line to the other side must measure 180 degrees. So 180 – 103 = 77 degrees.
Using this approach, I determined each angle the shelves make with the transversal. Since all corresponding angles between the pink shelf and the blue shelf are equal those shelves must be parallel.
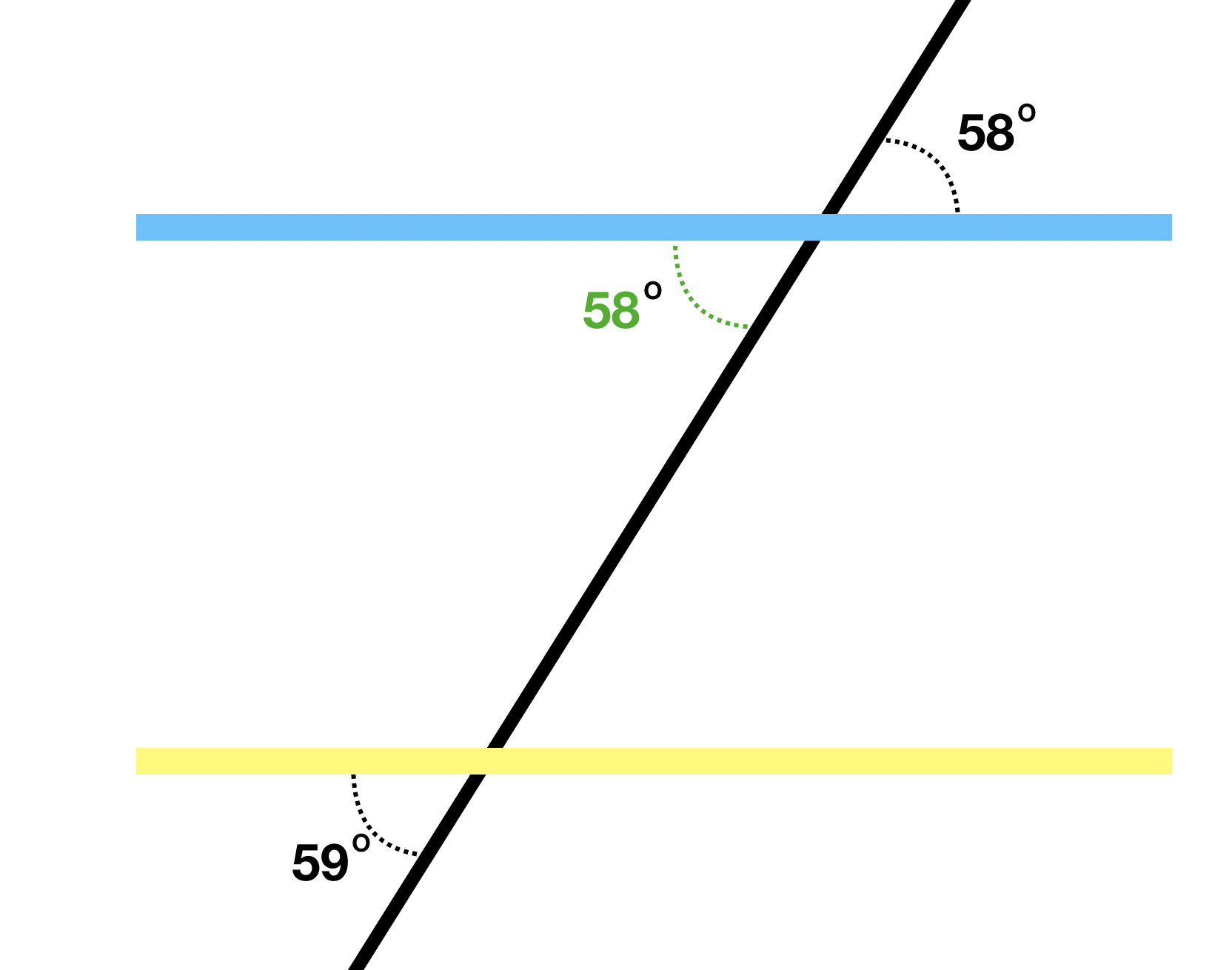
Student Approach #3: Opposite Angles
Strategy
I know opposite angles are equal so both of these angles are 58 degrees.
I also know that for parallel lines corresponding angles are equal and if these lines were parallel then the angle that measures 59 degrees between the yellow shelf and the transversal should also be 58 degrees. Since it’s not, these shelves are not parallel.
Note:
Even though each of these student responses determined only one (1) pair of shelves to be either parallel or not parallel please note that those same strategies could be applied to the remaining two pairs.
Next Moves
Reveal
After consolidating learning using student generated solution strategies and by extending their thinking intentionally, we can share which shelves are parallel. Show a video that clearly indicates that one shelf is parallel, while the other two shelves are not. Revisit the student answers. Have students discuss their thinking and what they would change if they did the task again. Return to the questions you recorded from the Spark portion of the lesson, and answer any questions that have not been answered.Consolidation
During the consolidation, use student generated solution approaches and strategies to facilitate a discussion intended to connect student approaches.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
How could you adjust each of the non-parallel shelves so that they become parallel?
Consolidation Prompt #2:
Create your own question to give to a peer: create two shelves that are either parallel or not parallel.
Include angle information in your diagram that makes it:
- easy to determine if the lines are parallel; and,
- another that is hard to determine if the lines are parallel.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
BLM Handout
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!