Students will demonstrate the concepts and skills that they have developed through this context and learning experience.

The purpose of this assessment is for students to demonstrate their understanding of the following big ideas.

• Multiplication can be interpreted as “groups of” or “parts of”, where the first factor is the number of groups, and the second factor is the quota;
• Multiplication can be represented using an array or area model;
• A part of a whole unit can be expressed as a fraction;
• A fraction described the number of parts relative to a whole;
• The fractional unit (the denominator) communicates how the whole is partitioned (number of parts);
• Equivalent values can be represented by different fractional notation (for example, \(\frac{1}{4} \) is equal to \(\frac{3}{12} \));
• The product when multiplying fractions is relative to the whole unit.
• Ratio reasoning is when the units represented by a ratio are scaled in tandem.

The independent assessment will allow students to demonstrate concepts and skills related to the following learning goals:

• I will solve problems that involve multiplying fractions.
• I will represent the multiplication of fractions using an area model.
• I will create a context to represent a multiplication sentence involving fractions.
• I will scale a ratio in tandem to determine an unknown quantity.

Students might write and/or model their answers independently. Students can also be interviewed by their teacher.

An alternative assessment opportunity should be offered if this tool will not successfully capture what the student knows, understands or can do.

In today’s math talk, students will determine unknown quantities in the ratio table.

Consider leveraging a bar model to help students make sense of these relationships.

We will build on the flooding the ice rink context from day 3 where the person in the video was pulling a cooler full of water to resurface the ice.

You might consider re-sharing the spark video to ensure all students understand and are comfortable with the context:

Ensure that students are comfortable with the context by re-telling the story using a script of your choice such as this one:

Remember from a couple days ago where we watched this person flood the ice rink to resurface the ice?

(pointing to screen as video plays)

Does anyone remember how this person was doing that?

Right! The person used a cooler, filled it up with warm water and dragged it over the ice surface.

Well, here’s the thing:

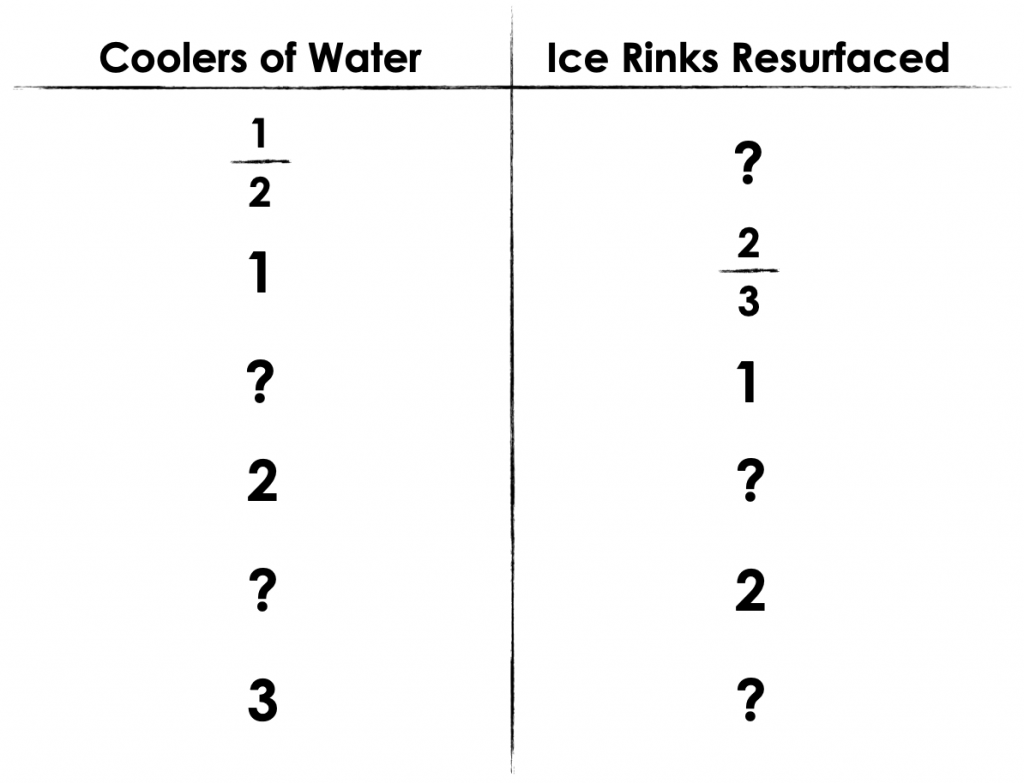
After doing this a few times, he realized that he can resurface approximately \(\frac{2}{3} \) of the whole ice rink with one whole cooler-full of water.

(Write this on the board)

Sometimes, the person is motivated to resurface more than once to really improve the quality of the ice rink.

Before setting off to do this work, this person thought they’d better get a sense of how many times they’ll need to re-fill the cooler.

Let’s try to help this person out a bit…

Long story, right? Well, context is so important in order to ensure all students have an understanding of what we are asking them to accomplish with this math talk.

Starting with 1 cooler full of water to resurface \(\frac{2}{3} \) of an ice rink, you can begin organizing thinking in a ratio table while modelling with a bar model (or double number line if students have experience with this more abstract tool).

Here’s the string in a ratio table for you to easily reference:

Here is how you might verbalize this string of related problems to stay true to the context:

• If 1 full cooler of water can flood \(\frac{2}{3} \) of the ice rink, then how much of the rink can you flood with \(\frac{1}{2} \) of a cooler of water?
• How many times do you need to fill the cooler with water to flood the entire ice rink?

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

Consider viewing the following walk through video where we demonstrate how this math talk might be facilitated:

Here is an animated version of the walk through that might be helpful to consolidate thinking after modelling you facilitate and model the math talk with your students:

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

Question #1:

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

Question #2:

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

Question #3:

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

Question #4:

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

Download Editable/Printable Handout

Become a member to access purposeful practice to display via your projector/TV, download the PDF to upload to your LMS and/or print for students to have a physical copy

JOIN TO DOWNLOAD